7 Der Arbeits- und Energiebegriff in der Elastostatik

F. U. Mathiak 7-1

7 Der Arbeits- und Energiebegriff in der Elastostatik

7.1 Die Arbeit einer Kraft längs eines Verschiebungswe- ges

Abb. 7-1 Arbeit einer Kraft längs eines Verschiebungsweges

Für die an einem starren Körper angreifende Kraft F, deren Angriffspunkt sich auf einer Bahnkurve C bewegt (Abb. 7-1), definieren wir die differentielle Arbeit längs des Verschie- bungsweges dr als das Skalarprodukt

α

= α

=

⋅

= d d cos ( ) Fdrcos

dA_a F(r) r F(r) r r _{Gl. 7-1}

Die skalare Größe dAa ist das Produkt aus der Kraftkomponente in Wegrichtung, also α

cos

F , und dem Verschiebungszuwachs dr, wenn Kraft- und Wegrichtung den Winkel α miteinander einschließen. Der Verschiebungszuwachs dr tangiert dabei an jeder Stelle r die Bahnkurve C. Auf dem endlichen Verschiebungsweg von r1 nach r2 verrichtet die Kraft die Arbeit

r r F

r

r

d ) ( A

2

1

a ⁼

∫

Sonderfall: Hängt die Kraft F=Fe_z nicht vom Verschiebungswege r ab, und sind Kraft und Verschiebungsdifferential dr=dze_z für den gesamten Verschiebungsweg parallel, dann geht Gl. 7-2 über in

) z z ( F dz F d ) (

A _{2 1}

z

z a

2

1 2

1

−

=

=

⋅

=^r

∫

∫

r

Gl. 7-3

Die Arbeit kann sowohl positiv, negativ oder auch Null sein. Die Definition wurde gerade so gewählt, daß bei positiver Arbeit Aa die Kraft F Arbeit verrichtet, während bei negativer Ar- beit Aa Arbeit gegen die Kraft aufgewendet werden muß. Für F⊥dr ist der differentielle Ar- beitsanteil dAa gleich Null. Die Arbeit hat die Dimension:

[ ]

) Zeit (

) Länge ( Masse

A ⋅

= Einheit: kgm²s⁻² =Nm=J

Ð

Beispiel: 7-1

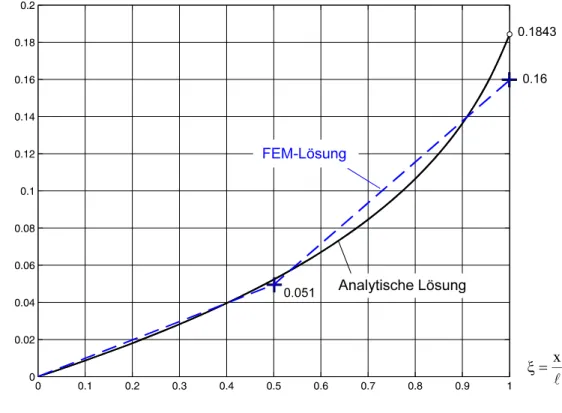
Gesucht wird die Arbeit einer linear veränderlichen Streckenlast (Abb. 7-2) an einem vorge- gebenen Verschiebungsweg

(

)

2 6 4

3 ) f x (

w = ξ − ξ+ξ .

(

)

Abb. 7-2 Kragträger mit linear veränderlicher Streckenlast

Wir führen die Lösung des Problems auf die Arbeit einer infinitesimalen Kraft dF längs des Verschiebungsweges w(x) zurück. Die Arbeit der differentiellen Kraft dF = q(x) dx am Ver- schiebungswege w(x) ist: dA_a =dF(x)w(x)=q(x)dxw(x)

F. U. Mathiak 7-3

Für die Arbeit der gesamten Linienlast q(x) gilt dann: A dA q(x)w(x)dx

0 x a

a

∫ ∫

=

=

= ^l .

Beachten wir − = +∆ ξ

+

= q q x q q

q ) x (

q _l ^{r l} _l

l , dann liefert die Integration

( ) ( )

⎠

⎜ ⎞

⎝

⎛ + ∆

= ξ ξ + ξ

− ξ ξ

∆ +

= ^f₃

∫

A

1

0

2 2

a l l l l

und für den Sonderfall Gleichstreckenlast erhalten wir mit q_r =q_l =q₀ und ∆q=0 f

q 4 , 0 5 f

q

A_a = 2 ⁰l = ₀l .

Achtung: Prinzipiell falsch wäre es, im Fall der Gleichstreckenlast mittels der Resultierenden l

q0

R = und dem zugehörigen Angriffspunkt ξ^* =l 2 sowie der dortigen Verschiebung 48f

) 17 (

w ξ^* = die Arbeit f 0,354q f

48 q ) 17 ( Rw

A_a = ξ^* = ⁰l = ₀l zu ermitteln.

Ï

7.2 Die Arbeit eines Kräftepaares mit dem Moment M

Abb. 7-3 Arbeit eines Kräftepaares Abb. 7-4 Momentane Drehachse

Die Arbeit eines Kräftepaares mit dem Moment M=r×F (Abb. 7-3) leiten wir unmittelbar aus der Definition Gl. 7-1 her. Nach Euler kann nämlich die infinitesimale Lageänderung (Abb. 7-4) eines Punktes P des starren Körpers darstellt werden als die Hintereinanderschal- tung einer für alle Körperpunkte identischen Translation drA und einer Rotation mit dem dif- ferentiellen Drehwinkel dϕ um den Punkt A, also

AP

A d

d

dr= r + ϕ×r _{Gl. 7-4}

Dabei ist A ein beliebiger Punkt des Körpers und rAP der Verbindungsvektor von A nach P.

Nach Gl. 7-1 ist die differentielle Arbeit des Kräftepaares:

( ) ( ) [ ( ) ]

( )

[

] (

) (

) ( )

ϕ ϕ

d M d r F d

r F r d F a a d F

a d dr a d r F r r F dr F r

d F

2 1

2 A

2 1

⋅

=

⋅

×

−

=

×

⋅

−

=

×

⋅

=

−

×

⋅

=

× +

−

× +

⋅

=

−

⋅

=

⋅

− +

⋅

= _{1 2 A 1}

a d d d

dA

Der translatorische Anteil hebt sich offensichtlich heraus, und es verbleibt ϕ

ϕ) d M( ⋅

a =

dA _{Gl. 7-5}

Dreht sich der Körper mit dem Kräftepaar von ϕ₁ bis ϕ₂, so wird die Arbeit

∫

= ²

1

Aa ϕ ϕ

ϕ ϕ) d

M( _{Gl. 7-6}

verrichtet.

Ð

Beispiel: 7-2

Gesucht wird die Arbeit eines Momentes M an der Verdrehung des Stabendes nach Gl. 7-7, wenn die Verschiebung ²

(

)

3 ) f x (

w = ξ − ξ+ξ vorgegeben ist.

Abb. 7-5 Balken mit Endmoment

Wird der Balken durch ein Moment M mit Drehrichtung um die negative y-Achse belastet, dann leistet dieses Moment Arbeit an der Tangentenneigung w', denn es gilt für kleine Ver- formungen tanϕ(x)≈ϕ(x)=w'(x) und damit

' Mw A

2

1

a =^ϕ

∫

ϕ

d M

Differentiation der Biegelinie nach x liefert:

( )

l l

l 3

f ) 4 x ( ' w 3

3 3 f ' 4

w = ξ − ξ+ξ² → = =

Für die Arbeit des Momentes erhalten wir dann:

l lf 3 M ) 4 ( ' Mw

A_a = =

Ï

F. U. Mathiak 7-5

7.3 Das Potential einer Kraft

Zur Auswertung des Integrals Gl. 7-2 ist in aller Regel die explizite Angabe der Bahnkurve C erforderlich, da sich mit der Lageänderung des Körpers im allgemeinen auch die Kraft F än- dert. Wir sprechen in diesem Fall von einem Kraftfeld F(r). In einem stationären¹ Kraftfeld ist F(r) nur vom Ort r abhängig, in einem instationären Kraftfeld hängt F(r,t) zusätzlich noch von der Zeit t ab.

1 2

(a) (b)

r₁ r₂

dr

F(r) P

Abb. 7-6 Bewegung einer Kraft auf einer geschlossenen Bahnkurve

Betrachten wir Abb. 7-6, dann ist i.a. A₁^(a₋⁾₂ ≠A₁^(b₋⁾₂. Ist jedoch die Arbeit vom Weg unabhän- gig, dann hängt sie nur vom Anfangs- und Endpunkt der Bahnkurve ab. Wir sprechen dann von einem konservativen² Kraftfeld. Wegunabhängigkeit

) b (

2 1 ) a (

2

1 A

A₋ = ₋ oder auch

0

1

) b ( 2 2

) a ( 1

=

⋅ +

⋅

∫

∫

ist gegeben, wenn gilt

0 A

) C (

a =

∫

Die Arbeit verschwindet demnach längs eines beliebigen geschlossenen Weges. Allgemein kann gezeigt werden, daß für ein Kraftfeld, das Gl. 7-7 genügt, ein Potential U(r) existieren muß, aus dem durch Gradientenbildung

1 von lat. stationarius ›stillstehend‹, ›zum Standort gehörig‹

2 zu lat. conservare ›bewahren‹, ›erhalten‹

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂ +∂

∂ +∂

∂

− ∂

=

−∇

=

−

= _{x y z}

z U y

U x

) U ( U )

( U

grad r r e e e

F _{Gl. 7-8}

das Kraftfeld F selbst gewonnen werden kann. Setzen wir nämlich Gl. 7-8 in Gl. 7-2, dann folgt unter Beachtung von

( )

dU z dz

dy U y dx U x U

dz dy

z dx U y

U x

U U _{x y z x y z}

∂ = +∂

∂ +∂

∂

= ∂

+ +

⎟⎟⋅

⎠

⎜⎜ ⎞

⎝

⎛

∂ +∂

∂ +∂

∂

= ∂

⋅

∇ dr e e e e e e

[

]

) ( dU )

( U

A _{2 1}

r

r r

r r

r 2 1

2

1 2

1 2

1

r r

r r

d r r

d

F(r)⋅ =− ∇ ⋅ =− =− −

=

∫ ∫ ∫

− Gl. 7-9

Die Wegunabhängigkeit eines konservativen Kraftfeldes begründet sich aus dem Sachverhalt, daß die Arbeit allein aus der Potentialdifferenz der Orte r2 und r1 gewonnen werden kann. Die Komponentendarstellung von Gl. 7-8 hinsichtlich einer kartesischen Basis liefert

⎥⎥

⎥⎥

⎥⎥

⎦

⎤

⎢⎢

⎢⎢

⎢⎢

⎣

⎡

∂

−∂

∂

−∂

∂

−∂

=

⎥⎥

⎥

⎦

⎤

⎢⎢

⎢

⎣

⎡

=

z Uy Ux U

F F F

z y x

F _{Gl. 7-10}

Die Rotation eines Vektorfeldes (hier des Kraftfeldes F) wird in der Vektoranalysis als Wir- bel des Vektorfeldes bezeichnet und symbolisch, unter Verwendung des Nablaoperators, in der Form rotF=∇×F geschrieben. Kraftfelder, die ein Potential besitzen, sind demnach wirbelfrei, denn es gilt:

0 e

e

e ⎟⎟⎠=

⎜⎜ ⎞

⎝

⎛

∂

∂

− ∂

∂

∂ + ∂

⎟⎠

⎜ ⎞

⎝

⎛

∂

∂

− ∂

∂

∂ + ∂

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂

∂

− ∂

∂

∂

= ∂

∇

×

∇

= y x

U y

x U z

x U x

z U y

z U z

y U U

gradU

rot _x ^{2 2} _y ^{2 2} _z ^{2 2}

Das Potential U(x,y,z) des Kraftfeldes muß also den folgenden Integrabilitätsbedingungen genügen:

x 0 y

U y

x

; U z 0 x

U x

z

; U y 0 z

U z

y

U ^{2 2 2 2 2}

2 =

∂

∂

− ∂

∂

∂

= ∂

∂

∂

− ∂

∂

∂

= ∂

∂

∂

− ∂

∂

∂

∂ Gl. 7-11

F. U. Mathiak 7-7

7.3.1 Das Potential einer Gewichtskraft

Als Beispiel einer Kraft, der ein Potential zugeordnet werden kann, betrachten wir die Ge- wichtskraft G eines schweren Körpers in der Nähe der Erdoberfläche (Abb. 7-7).

Abb. 7-7 Arbeit der Gewichtskraft G

Die Gewichtskraft G=−Ge_z hat in dem gewählten Koordinatensystem nur eine Komponen- te. Mit dem Ortsvektordifferential dr=dxe_x +dye_y +dze_z erhalten wir zunächst

dz G r

dA_a =G⋅d =− _{Gl. 7-12}

Integrieren wir diesen Ausdruck längs des Verschiebungsweges von r1 nach r2, also

( ) (

)

z

z

1 2 2

1 Gdz G z z G z z

A

2

1 2

1

−

=

−

−

=

−

=

⋅

=

∫ ∫

− r

r

dr G

dann erhalten wir die Arbeit der Gewichtskraft G, die offensichtlich nur von den z- Koordina- ten der beiden Endpunkte abhängt. Das Potential der Gewichtskraft folgt aus Gl. 7-10 zu

dAa

Gdz dz dU

G =−dU → = =−

−

nach Integration zwischen den beiden Lagen r1 und r2

) z z ( G U

U₂ − ₁ = ₂ − _{1 Gl. 7-13}

Nehmen wir das Nullniveau bei z2 = 0 an (U2 = 0), dann hat der Körper mit der Gewichtskraft G bezüglich der Ebene NN die Energie der Lage oder die potentielle Energie

h G

U= _{Gl. 7-14}

Die Dimension dieser skalaren Größe ist

[ ]

) Zeit (

) Länge ( Masse

U ₂ ^{2 2}

2 = =

= ⋅ ⁻

Die potentielle Energie kann anschaulich gedeutet werden als diejenige Energie, die benötigt wird, um G vom Nullniveau (z = 0) um z anzuheben. Sie ist > 0, wenn sich der Schwerpunkt oberhalb des Nullniveaus befindet, Null, wenn der Schwerpunkt im Nullniveau liegt und < 0, wenn er sich unterhalb desselben befindet.

7.3.2 Das Potential einer Federkraft

Abb. 7-8 Lineare Feder, Kraft-Verformungsdiagramm

Als weiteres Beispiel für eine konservative Kraft betrachten wir die äußere Kraft F=cxe_x, die eine lineare Feder mit der Federkonstanten c aus der ungespannten Lage (x = 0) in die Lage x auslenkt (Abb. 7-8). Nach Gl. 7-2 leistet die Kraft dabei die Arbeit

2Fx cx 1 2 x 1 d x c x d ) x ( F

A ²

x

0 x x

0 x

a =

∫

∫

=

=

Gl. 7-15

F. U. Mathiak 7-9

In Gl. 7-15 wurde dr =dxe_x berücksichtigt. Die Federkraft F_f leistet als Reaktionskraft dann die innere Arbeit

2Fx cx 1

2 x 1 d ) x ( F

A ²

x

0 x

f =−

∫

=

Gl. 7-16

Zur Berechnung des Potentials der Federkraft beachten wir Gl. 7-10 und erhalten

dx cx cx dU

dx F dU

F_x ≡ _f =− ^f =− → ^f =

Integration liefert:

2

f cx

2

U = 1 _{Gl. 7-17}

Geometrisch entspricht das Potential der Federkraft Uf der in Abb. 7-8 schraffierten Dreiecks- fläche unterhalb der linearen Kraft-Verschiebungskurve. Auch das Potential Uf ist nur bis auf eine (additive) Konstante festgelegt.

Entsprechende Beziehungen lassen sich für eine Drehfeder mit der Federkonstanten cd herlei- ten. Ist M=c_dϕe_y das äußere Moment, das die lineare Feder aus der ungespannten Lage

=0

ϕ in die Lage ϕ auslenkt, dann folgt unter Beachtung von dϕ =dϕe_y die dabei vom äußeren Moment geleistete Arbeit

ϕ

= ϕ

= ϕ ϕ

= ϕ ϕ

=

∫ ∫

= ϕ ϕ

= ϕ

2M c 1

2 d 1 c d

) ( M

A _d ²

0 d 0

a Gl. 7-18

Für das Federmoment M_f =−M ist dann analog zu Gl. 7-17

2 d

f c

2

U =1 ϕ _{Gl. 7-19}

Hinweis: Zu den Kräften, die sich nicht aus einem Potential ableiten lassen, gehören z.B. die geschwindigkeitsabhängigen Reibungskräfte, die dem Materialgesetz

)v v (

f v

R=− mit f(v)>0 genügen. Unter Beachtung von dt dt

r drdt v

d = = liefert Gl. 7-7

0 dt v ) v ( f v dt

) v ( f r

A_a =

∫

∫

∫

eine Arbeit, die immer negativ ist. Wegen A_a ≠0 lässt sich ein Potential nicht nachweisen.

Da diese Kräfte Arbeit zerstreuen, werden sie auch dissipative Kräfte¹ genannt. Zur Berech- nung der Arbeit einer dissipativen Kraft muß deshalb der vollständige Verschiebungszustand des Kraftangriffspunktes bekannt sein.

7.4 Formänderungs- und Ergänzungsenergie für elasti- sche Körper

Wir betrachten in einem ersten Schritt einen elastischen Körper, dessen Ausgangszustand spannungs- und verzerrungsfrei ist. Dieser Körper sei einem einachsigen Spannungs- und Deformationszustand unterworfen. Die einzigen von Null verschiedenen Spannungs- und Verzerrungskomponenten sind dann z.B. σ_xx und ε_xx. Ist die Spannung σ_xx eine allgemeine Funktion von ε_xx, also

) ( f _xx

xx = ε

σ _{Gl. 7-20}

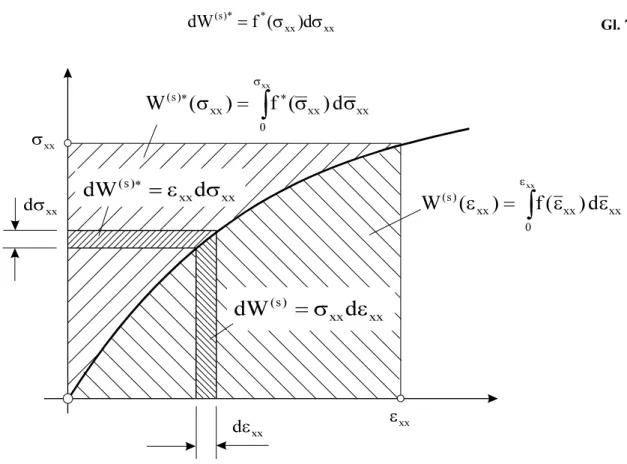
dann definieren wir als Differential der spezifischen² Formänderungsenergie (Abb. 7-9)

xx xx )

s

( f( )d

dW = ε ε _{Gl. 7-21}

Nach Integration über den gesamten Verzerrungszustand erhalten wir die spezifische Form- änderungsenergie

ε

∫

= ε

ε ε

=

ε ^xx

xx 0

xx xx xx

) s

( ( ) f( )d

W _{Gl. 7-22}

Fassen wir umgekehrt die Dehnungen als Funktion der Spannungen auf, also )

( f^* _xx

xx = σ

ε _{Gl. 7-23}

dann definieren wir als Differential der spezifischen Ergänzungsenergie (Abb. 7-9)

1 zu lat. dissipare ›zerstreuen‹, ›verschwenden‹

2 auf die Volumeneinheit bezogen

F. U. Mathiak 7-11

xx xx

*

* ) s

( f ( )d

dW = σ σ _{Gl. 7-24}

Abb. 7-9 Spezifische Formänderungs- und Ergänzungsenergie

Nach Integration über den gesamten Spannungszustand erhalten wir die spezifische Ergän- zungsenergie

xx

xx

(s)* *

xx xx xx

0

W ( ) f ( ) d

σ σ =

σ =

∫

Aus Abb. 7-9 wird auch deutlich, warum W^(s)* spezifische Ergänzungsenergie genannt wird.

Sie ergänzt offensichtlich die spezifische Formänderungsenergie, die sich im eindimensiona- len Fall geometrisch als die Fläche unterhalb der Kurve σ_xx =f(ε_xx) interpretieren läßt, zu einem Rechteck der Größe

(s) (s)*

xx xx

W +W = σ ε _{Gl. 7-26}

Die spezifische Formänderungsenergie und auch die Ergänzungsenergie haben Potentialcha- rakter, denn aus Gl. 7-21 und Gl. 7-24 folgen unmittelbar

(s)

xx xx

xx (s)*

*

xx xx

xx

dW f ( )

d

dW f ( )

d

= ε = σ ε

= σ = ε

σ

Gl. 7-27

oder in Worten:

1. Die spezifische Formänderungsenergie ist das Potential der Spannung.

2. Die spezifische Ergänzungsenergie ist das Potential der Verzerrung.

Abb. 7-10 Linear elastisches Material, Formänderungs- und Ergänzungsenergie

Bei linear elastischem Material sind im isothermen Fall (T = 0) die Maßzahlen für die spezifi- sche Formänderungsenergie und die spezifische Ergänzungsenergie gleich. Hier gilt nämlich nach Hooke: σ_xx =Eε_xx und damit

(s) (s)* 2 2

xx xx xx xx

E 1 1

W W

2 2E 2

= = ε = σ = σ ε

In Verallgemeinerung auf den dreidimensionalen Fall erhalten wir die spezifische Formände- rungsenergie für Hookesches Material in Matrizenschreibweise

( )

σ^{T T T}

(s)

2 1 2

1 2

W =1 = = _{Gl. 7-28}

Ausrechnen von Gl. 7-28 liefert in kartesischen Koordinaten

( ) ( )

⎢⎣⎡ + + + + +

+ − + +

= _xx² _yy² _zz² _{xx yy zz} ² _xy² _yz² _zx²

(s) γ γ γ

2 ε 1

ε ν ε

2 1 ε ν ε ε G

W Gl. 7-29

F. U. Mathiak 7-13

und unter Beachtung von ε=Lu gilt weiter

u) L D L (u Dε

ε^{T T T}) ( 2

1 2

W^(s) = 1 = _{Gl. 7-30}

Die Auswertung der rechten Seite von Gl. 7-30 liefert

⎪⎪

⎪

⎭

⎪⎪

⎪

⎬

⎫

⎪⎪

⎪

⎩

⎪⎪

⎪

⎨

⎧

⎥⎥

⎦

⎤

⎢⎢

⎣

⎡ ⎟

⎠

⎜ ⎞

⎝

⎛

∂ +∂

∂ + ∂

⎟⎠

⎜ ⎞

⎝

⎛

∂ +∂

∂ + ∂

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂ +∂

∂ + ∂

⎟⎟ +

⎠

⎜⎜ ⎞

⎝

⎛

∂ +∂

∂ +∂

∂

∂ + −

⎟⎠

⎜ ⎞

⎝

⎛

∂ + ∂

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂ + ∂

⎟⎠

⎜ ⎞

⎝

⎛

∂

∂

= 2 2 2

2 2 2 2

(s)

z x x z v

z z v x

v y u 2 1

z w y v x u ν 2 1

ν z

w y

v x

u G

W Gl. 7-31

Die Formänderungsenergie ergibt sich in jedem Fall durch Integration der spezifischen Form- änderungsenergie über das Gesamtvolumen des betrachteten Körpers.

∫

=

(V)

(s)dV W

W _{Gl. 7-32}

7.5 Formänderungsenergie für den geraden Balken

Wir beschränken uns auf linear elastisches Material. Für die folgenden Untersuchungen wird der isotherme Fall mit T = 0 zugrunde gelegt.

7.5.1 Schiefe Biegung mit Normalkraft

Von den Verzerrungen verbleibt nur die Dehnung ε_xx =u′−zw′′−yv′′. Alle anderen Verzer- rungen sind Null. Die spezifische Formänderungsenergie Gl. 7-29 reduziert sich unter Beach- tung von ν=0 und G = E/2 auf

( )

(

)

2 2

xx )

s (

v y v w yz 2 w z v y u 2 w z u 2 2 u

E

v y w z 2 u E 2

W E

+ ′′

′′

+ ′′

+ ′′

′′

− ′

′′

− ′

= ′

− ′′

− ′′

= ′ ε

=

und mit dV=dAdx erhalten wir bei Bezugnahme auf Hauptzentralachsen

dA dx y ) x ( v dA yz ) x ( v ) x ( w 2 dA z ) x ( w

dA y ) x ( v ) x ( u 2 dA z ) x ( w ) x ( u 2 dA ) x ( u

2 dV E W W

0 x

I ) A (

2 2

0 ) A ( I

) A (

2 2

0 ) A ( 0

) A ( A

) A ( 2

) V (

) s (

zz yy

∫ ∫ ∫ ∫

∫

∫

∫

∫

=

=

=

=

=

=

⎥⎥

⎥⎥

⎥⎥

⎦

⎤

⎢⎢

⎢⎢

⎢⎢

⎣

⎡

+ ′′

′′

+ ′′

+ ′′

′′

′

−

′′

′

−

′

=

= ^l

3 2 1 43

2 1 3

2 1

3 2 1 3

2 1 3

2 1

Nach Zusammenfassung verbleibt

[

]

2 W 1

0 x

2 zz 2

yy

∫

=

+ ′′

+ ′′

= ^l ′ _{Gl. 7-33}

Die spezifische isotherme Formänderungsenergie läßt sich unter Beachtung von

⎥⎥

⎦

⎤

⎢⎢

⎣

⎡ + −

σ =

=

ε y

I ) x ( z M I

) x ( M A

) x ( N E 1

E _zz

z yy

xx y xx

auch als Funktion der Schnittlasten N(x), My(x) und Mz(x) darstellen:

2

zz z yy

y 2

xx )

s

( y

I ) x ( z M I

) x ( M A

) x ( N E 2

1 2

W E

⎥⎥

⎦

⎤

⎢⎢

⎣

⎡ + −

= ε

=

Integration über das Stabvolumen führt auf

EI dx ) x ( M EI

) x ( M EA

) x ( N 2 W 1

0

x zz

2 z yy

2 2 y

∫

⎦

⎤

⎢⎢

⎣

⎡ + +

= ^l _{Gl. 7-34}

Beispiel: 7-3

Für den durch eine Normalkraft F und eine Linienlast q0 belasteten Kragträger ist die Formänderungsenergie zu berechnen.

Lösung: Aus Gleichgewicht ergeben sich die Schnittlasten:

N = F = konst.; _y ⁰

(

)

2 ) q x (

M =− l−

Mit Gl. 7-34 erhalten wir dann

F. U. Mathiak 7-15

( )

yy 5 2 0 2

0 x

4 yy

2 0 2

0

x yy

2 2 y

EI 40

q 2EA dx F

4EI x q EA

F 2 dx 1 EI

(x) M EA

(x) N 2

W 1 l l l

l

l = +

⎥⎥

⎦

⎤

⎢⎢

⎣

⎡ + −

⎥ =

⎥⎦

⎤

⎢⎢

⎣

⎡ +

=

∫ ∫

=

=

Hinweis: Die Verschiebung u eines Dehnstabes infolge Einzellast F am Stabende ist bekannt- lich

EA

u= Fl . Die Arbeit der Kraft F an dieser Verschiebung ist nach Gl. 7-15

EA 2 Fu F 2

A= 1 = ²l

und damit identisch mit der im Körper gespeicherten Formänderungsenergie, die z.B. dazu genutzt werden kann, den Körper bei der Entlastung wieder in seinen Ausgangszustand zu bringen.

7.5.2 Querkraftbeanspruchung

Für den schubelastischen Balken gilt:

(

)

2 1 2

1

y y

xz = ϕ = ω + ′

ε . Mit Gl. 7-29 finden wir dann

2y )

S

( G

2 W = 1 ϕ

und nach Integration über das Gesamtvolumen des Stabes

dx ) x ( 2 GA W 1

0 x

2y

∫

ϕ

= ^l _{Gl. 7-35}

Unter Beachtung des Werkstoffgesetzes für die Querkraft Q_z =GAϕ_y können wir mit Gl.

7-35 auch

GA dx ) x ( Q 2 W 1

0 x

2

∫

=

= ^l _{Gl. 7-36}

schreiben. Durch formale Erweiterung auf den zweidimensionalen Fall erhalten wir in Erwei- terung von Gl. 7-35

dx ) x ( 2 GA

dx 1 ) x ( 2 GA

W 1

0 x

2 z 0

x

2

y

∫

∫

ϕ +

ϕ

= ^{l l} _{Gl. 7-37}

Und entsprechend von Gl. 7-36

GA dx ) x ( Q 2 dx 1 GA

) x ( Q 2 W 1

0 x

2y

0 x

2

z

∫

∫

+

= ^{l l} _{Gl. 7-38}

Im Fall des schubstarren Balkens liegt kein Stoffgesetz für die Querkräfte vor. Wir gehen deshalb von den aus Gleichgewichtsbetrachtungen ermittelten Schubspannungen

) z ( b ) x ( I

) z ( S ) x ( Q

yy y z xz = σ aus. Mit Gl. 7-25 erhalten wir

2

yy y 2 z

xz )

S ( ) S (

) z ( b ) x ( I

) z ( S ) x ( Q G 2

1 G

2 W 1

*

W ⎥⎥

⎦

⎤

⎢⎢

⎣

= ⎡ σ

=

= und damit

) dx x ( A ) x ( I

) x ( A ) x ( dz Q ) z ( b

) z ( S

dzdx ) z ( ) b z ( b ) x ( I

) z ( S ) x ( Q G 2 dAdx 1 ) z ( b ) x ( I

) z ( S ) x ( Q G 2 dV 1 G

1 2 W 1

0 x

2 2 z z

z z

2 y

) V (

2 2

2 y 2 z )

V (

2 2

2 y 2 z )

V (

2 xz

yy u

o

yy yy

∫ ∫

∫

∫

∫

= = ⎥⎥

⎦

⎤

⎢⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

= ⎛

=

= σ

=

l

Die obige Beziehung können wir noch etwas kompakter schreiben, wenn wir den dimensions- losen Querschnittswert

=

∫

=

κ ^u

o 2

z

z z

2 y yy

z dz

) z ( b

) z ( S ) x ( I

) x ( ) A x

( _{Gl. 7-39}

einführen. Wir erhalten dann die Formänderungsenergie

∫

κ

= ^l

0 x

2

z z dx

) x ( A

) x ( )Q x G (

2

W 1 _{Gl. 7-40}

Ð Beispiel 7-1: Gesucht wird die Formänderungsenergie für einen Balken mit Rechteckquer- schnitt der Breite b und der Höhe h.

Lösung:

⎥⎥

⎦

⎤

⎢⎢

⎣

⎡ ⎟

⎠

⎜ ⎞

⎝

−⎛

=

2 2

y h

z 1 2 8 ) bh z (

S . Für den Querschnittswert erhalten wir

(

)

b dz ) z ( S I

A ^{2 5}

5 2 2

/ h

2 / h z

2 2 y

3 2

/ h

2 / h z

2 y yy

z = ² = = =

κ

∫ ∫

−

=

−

=

und damit

F. U. Mathiak 7-17

∫

= ^l

0 x

2 z(x)dx GA Q

5 W 3

Beispiel 7-2: Gesucht wird die Formänderungsenergie eines Balkens mit Kreisquerschnitt (Ra- dius a).

2 2 3 3

y 4 yy 2

a 1 z 3a ) 2 z ( S 4 ; I a

; a

A ⎥⎥

⎦

⎤

⎢⎢

⎣

⎡ ⎟

⎠

⎜ ⎞

⎝

−⎛ π =

= π

= ;

2

a 1 z a 2 ) z (

b ⎟

⎠

⎜ ⎞

⎝

−⎛

= ; dA=b(z)dz

6 5

a

0 z

2 2 5 5

a

a z

2

y a

72 a 5 32 a 5 9 dz 4 a

1 z 9a

dz 4 ) z ( b

) z (

S = π = π

⎥⎥

⎦

⎤

⎢⎢

⎣

⎡ ⎟

⎠

⎜ ⎞

⎝

−⎛

=

∫

∫

=

9 a 10 72

5 4 a dA a ) z ( b

) z ( S I

A 6

4 2 2

) A (

2 2 y yy

z ² π =

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛ π

= π

=

κ

∫

und damit

∫

= ^l

0 x

2 z(x)dx GA Q

9 W 5

Ï

Für den Fall der schiefen Biegung mit Qz und Qy werden die oben hergeleiteten Beziehungen sinnvoll erweitert. Wir erhalten entsprechend Gl. 7-40

∫

∫

κ + κ

= ^{l l}

0 x

2 y y 0

x

2

z z dx

GA ) x ( )Q x 2 (

dx 1 GA

) x ( )Q x 2 (

W 1 _{Gl. 7-41}

Bei dünnwandigen Walzprofilen (I-Profil, U-Profil usw.) wird die Querkraft Qz vorwiegend durch den Steg abgetragen. Bezeichnet A die Querschnittsfläche des Gesamtquerschnittes und ASteg die Querschnittsfläche des Steges, dann kann näherungsweise

Steg

z A

= A

κ _{Gl. 7-42}

gesetzt werden.

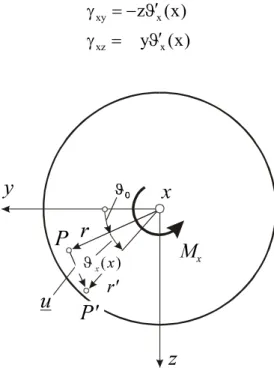
7.5.3 Torsion

Wir beschränken uns auf den wölbfreien Kreis- bzw. Kreisringquerschnitt. Für den Verschie- bungsvektor gilt

)]

x ( y );

x ( z

; 0

[ − ϑ_x ϑ_x

= u mit den daraus resultierenden Gleitungen

) x ( y

) x ( z

x xz

x xy

ϑ′

= γ

ϑ′

−

= γ

Abb. 7-11 Torsion eines kreisförmigen Balkens

Alle anderen Verzerrungen sind Null. Mit Gl. 7-29 erhalten wir

( )

r z y 2( G 2

W G _x²

2 2 2 2

xz 2 xy )

s

( ϑ′

= +

= γ + γ

= 123

und nach Integration über das Stabvolumen

∫

∫ ∫

=

ϑ′

= ϑ′

= ^{l l}

3 2

1 ^{x 0}

2 x p 0

x

2 x

I ) A (

2 GI dx

2 dx 1 ) dA r ( 2 G W 1

p

Gl. 7-43

Beachten wir noch das Werkstoffgesetz

p x x

GI ) M x ( ) x (

D ≡ϑ′ = , dann lässt sich die in einem tor- dierten Stab gespeicherte Formänderungsenergie auch durch das Schnittlastmoment Mx aus- drücken:

F. U. Mathiak 7-19

∫

= ^l

0

x p

2

x dx

GI ) x ( M 2

W 1 _{Gl. 7-44}

Liegt eine kombinierte Beanspruchung vor, dann dürfen die Einzelbeanspruchungen zur Ge- samtlösung superponiert werden. Die Addition sämtlicher Formänderungsanteile liefert:

GI dx ) x ( M GA

) x ( Q GA

) x ( Q EI

) x ( M EI

) x ( M EA

) x ( N 2 W 1

0

x p

2 x 2

y y 2

z z zz 2 z yy

2 2 y

∫

⎦

⎤

⎢⎢

⎣

⎡ + + +κ +κ +

= ^l

Normalkraft Biegung Querkraft Torsion

∫

= ^l ′

0 x

2(x)dx u

2 EA W 1

∫

∫

=

=

+ ′′

= ′′

l l

0 x

2 zz 0 x

2 yy

dx ) x ( v 2 EI 1

dx ) x ( w 2 EI

W 1

dx ) x ( 2 GA

1

dx ) x ( 2 GA

W 1

0 x

2 z 0 x

2y

∫

∫

=

=

ϕ +

ϕ

=

l l

(schubelastischer Balken)

∫

ϑ′

= ^l

0 x

x2

p dx

2 GI W 1

∫

= ^l

0 x

2

EA dx ) x ( N 2 W 1

∫

∫

=

=

+

=

l l

0

x zz

2 z 0

x yy

2 y

EI dx ) x ( M 2 1

EI dx ) x ( M 2 W 1

∫

∫

=

=

κ +

κ

=

l l

0 x

2 y y

0 x

2 z z

GA dx ) x ( Q 2 1

GA dx ) x ( Q 2 W 1

(schubstarrer Balken)

∫

= ^l

0

x p

2x dx

GI ) x ( M 2 W 1

Tabelle 7-1 Formänderungsenergien für den geraden Stab bei linear elastischem Materialverhalten

Hinweis: Der Anteil der Formänderungsenergie aus Querkraft ist im Vergleich zu den übrigen Beanspruchungen von untergeordneter Bedeutung und wird deshalb in praktischen Berech- nungen oftmals vernachlässigt.

7.6 Die isotherme Formänderungsenergie für die Scheibe

Die Scheibenebene liege parallel zur x-y-Ebene. Es gilt der ebene Spannungszustand mit dem Verschiebungsvektor

) v , u (

T =

u und den daraus abgeleiteten Verzerrungen

[ ]

⎦

⎢ ⎤

⎣

⎡

∂ +∂

∂

∂

∂

∂

∂

= ∂ γ ε ε

= x

v y , u y , v x , u

, _{yy xy}

xx

εT

sowie der Materialmatrix

⎥⎥

⎥⎥

⎥⎥

⎦

⎤

⎢⎢

⎢⎢

⎢⎢

⎣

⎡

− −

=

2 ν 0 1

0

0 1 ν

0 ν 1

ν 1

E

ES 2

D

Für die spezifische Formänderungsenergie erhalten wir dann

⎥⎦⎤

⎢⎣⎡ + + ν + −νγ

= −

= _{2 xx}² _yy² _{xx yy xy}²

(s)

2 ε 1

ε 2 ε ) ε

ν 1 ( 2

E 2

W 1ε^TD_ESε _{Gl. 7-45}

und unter Beachtung von ε=Lu

⎥⎥

⎦

⎤

⎢⎢

⎣

⎡

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂ +∂

∂

∂ ν + −

∂

∂

∂ ν∂

⎟⎟ +

⎠

⎜⎜ ⎞

⎝

⎛

∂ + ∂

⎟⎠

⎜ ⎞

⎝

⎛

∂

∂

= −

=

2 2 2

2 (s)

x v y u 2 1 y v x 2 u y v x

u ) ν 1 ( 2

E 2

W 1(Lu)^TD_ES(Lu)

Gl. 7-46

Die Formänderungsenergie der gesamten Körpers ist dann (Scheibendicke h)

( )

∫∫

∫∫

=

A (A)

(s) dA

2 dA h W h

W (Lu)^TD_ES(Lu) _{Gl. 7-47}

7.7 Formänderungsenergie für die schubstarre Platte

Die Plattenmittelfläche liege in der x-y-Ebene. Die Verschiebung

⎟⎟⎠

⎜⎜ ⎞

⎝

⎛

∂

− ∂

∂

− ∂

=

= y

z w x , z w )

v , u

T ( u

eines Punktes P mit dem Abstand z von der Plattenmittelfläche läßt sich durch die Änderung des Verschiebungsfeldes w(x,y) ausdrücken. Daraus ergeben sich die Verzerrungen

F. U. Mathiak 7-21

[ ]

y x 2 w y , , w x , w

, _{yy xy} ² ₂ ² ₂ ^{2 T}

xx

T κ

ε ⎥ =

⎦

⎢ ⎤

⎣

⎡

∂

∂

− ∂

∂

−∂

∂

−∂

= γ ε ε

=

Mit der Materialmatrix für den ebenen Spannungszustand

⎥⎥

⎥⎥

⎦

⎤

⎢⎢

⎢⎢

⎣

⎡

ν ν −

ν ν

= −

2 0 1 0

0 1

0 1

1 E D 2

folgt für die Spannungen σ=Dε und damit die spezifische Formänderungsenergie

Dκ κ Dε ε ε

σ^{T T 2 T}

) s (

2 z 2

1 2

W = 1 = = _{Gl. 7-48}

Ausrechnen liefert

( )

⎪⎬

⎫

⎪⎩

⎪⎨

⎧ ⎥

⎦

⎢ ⎤

⎣

⎡ ⎟⎟

⎠

⎜⎜ ⎞

⎝

⎛

∂

∂

− ∂

∂

∂

∂ ν ∂

−

− ν ∆

= −

y x

w y

w x ) w 1 ( 2 ) w

1 ( 2

W^(s) Ez² ₂ ^{2 2} ₂ ²₂ ² _{Gl. 7-49}

In jedem Fall ist die Formänderungsenergie der gesamten Platte

2 dA dA 1 12

h 2 dV 1 W W

) A (

T )

A ( 3 T )

V (

) s

(

∫∫ ∫∫

∫

= κ Dκ κ D_PLκ _{Gl. 7-50}

wobei

⎥⎥

⎥⎥

⎦

⎤

⎢⎢

⎢⎢

⎣

⎡

ν ν −

ν ν

= −

2 0 1 0

0 1

0 1

) 1 ( 12

Eh

2 3

DPL

die Materialmatrix der Plattenbiegung bezeichnet.

8 Das Prinzip der virtuellen Verrü- ckung

In der Statik bilden die beiden Axiome

− Kraftgleichgewicht und

− Momentengleichgewicht

die Grundlage zur Berechnung mechanischer Systeme. Neben diesen Grundgesetzen wer- den außer dem Befreiungsprinzip und dem Schnittprinzip bei Systemen starrer Körper die kinematischen Beziehungen und bei deformierbaren Körpern zusätzlich geeignete Materialgesetze benötigt. Die Vorgehensweise bei der Lösung mechanischer Probleme ist dabei immer dieselbe.

Systeme starrer Körper:

1. Befreiung des Systems von den Auflagern, Anbringen der Auflagerreaktionslasten nach dem Befreiungsprinzip,

2. Zerschneiden des Systems, Anbringen der Schnittlasten nach dem Schnittprinzip, 3. Anwendung der Gleichgewichtsbedingungen auf jedes freigeschnittene Teilsystem, 4. Formulierung der kinematischen Beziehungen für das Starrkörpersystem,

5. Berechnung der Auflager- und Schnittkräfte.

Deformierbare Körper:

1. Herausschneiden eines Volumenelements,

2. Anwendung der Gleichgewichtsbedingungen auf das Element,

3. Aufstellen der kinematischen Beziehungen, also den Beziehungen zwischen den Verschiebungen und den Verzerrungen,

4. Wahl eines Materialgesetzes,

5. Elimination der Spannungen führt auf ein System partieller Differentialgleichungen für die Verschiebungen, den Lamé-Navierschen Verschiebungsdifferentialglei- chungen, Elimination der Verschiebungen führt auf die Beltrami-Michellschen Spannungsdifferentialgleichungen,

6. Lösung des Gleichungssystems unter Berücksichtigung der Randbedingungen lie- fert die vollständige Deformation des Körpers.

In vielen Fällen kann sich diese Vorgehensweise jedoch als recht umständlich erweisen.

Bei Systemen starrer Körper interessieren häufig die Schnittkräfte gar nicht. In diesen

8-2 Das Prinzip der virtuellen Verrückung

Fällen müssen, insbesondere bei großen Systemen, viele überflüssige Unbekannte mit berechnet werden. Bei deformierbaren Systemen ist oft der Deformationszustand des gesamten Systems nicht gefragt. Nicht selten reicht es aus, Zustandsgrößen an einzelnen Punkten zu berechnen (Verschiebungen, Auflagerkräfte bei statisch unbestimmten Sys- temen). In diesen Fällen wird bei der Integration meist komplizierter Differentialglei- chungen viel überflüssige Arbeit geleistet. Für die praktisch interessanten Fälle ist eine analytische Integration der anfallenden partiellen DGLn meist ohnehin nicht möglich. Für solche Fälle benötigen wir Näherungsverfahren, mit denen wir bei möglichst geringem Rechenaufwand eine gute Annäherung an die theoretisch exakte Lösung erreichen. Dazu dienen die Energieprinzipien der Mechanik, die folgende Vorteile bieten:

1. Angewandt auf starre Körper oder Systeme von starren Körpern erlauben sie eine schnelle Herleitung der Gleichgewichtsbedingungen ohne Kenntnis der Schnittgrö- ßen.

2. Angewandt auf deformierbare Körper ermöglichen sie die Ermittlung von Kräften oder Verschiebungen an einzelnen Körperpunkten ohne Kenntnis der Lösung der Grundgleichungen (Sätze von Castigliano).

3. Außerdem bilden sie die Grundlage zur Herleitung von Näherungsverfahren, wie dem Verfahren von Ritz und der Methode der Finiten Elemente (FEM), die sehr eng mit dem Ritzschen Verfahren verbunden ist.

Das Prinzip der virtuellen¹ Verrückung ist eine den Gleichgewichtsbedingungen äquivalente Energieaussage, das sowohl für starre als auch für deformierbare Kör- per formuliert werden kann.

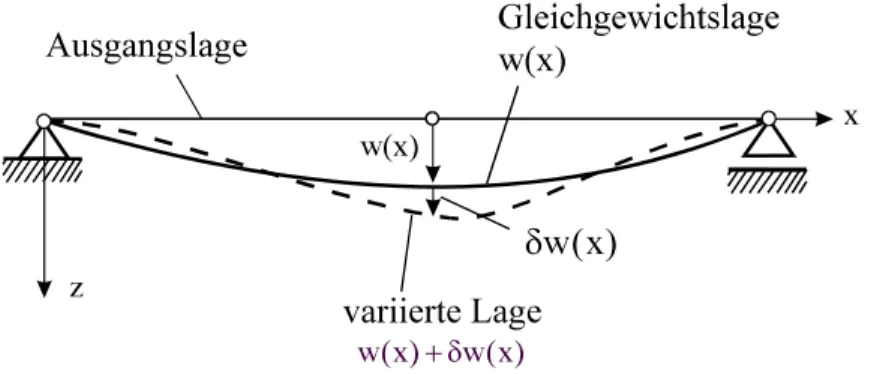
Abb. 8-1 Beispiel einer virtuellen Verrückung am beidseitig drehbar gelagerter Balken

1 virtualis zu lat. virtus ›Tüchtigkeit‹, ›Mannhaftigkeit‹, fachsprachlich für nicht wirklich; scheinbar; ge- dacht.

Definition: Eine virtuelle Verrückung δu ist eine dem aktuellen Deformationszustand zusätzlich überlagerte Verschiebung (Variation des Verschiebungszustandes) mit den folgenden Eigenschaften:

1. δu ist geometrisch möglich, d.h. bei der virtuellen Verrückung wird der Zusammen- hang des Körpers gewahrt. δu ist verträglich (kompatibel) mit den Lagerungsbedin- gungen.

2. Die Verrückung δu ist differentiell klein. Damit können in allen Rechnungen Terme von höherer Ordnung als klein gestrichen werden.

3. Sämtliche inneren und äußeren Kraftgrößen werden bei der Durchführung der Variati- on δu konstant gehalten, d.h. nicht variiert.

4. Die virtuelle Verrückung ist eine gedachte Verrückung bei festgehaltener Zeit. Dabei ist uninteressant, in welcher Zeit wir uns diese virtuelle Verrückung entstanden den- ken.

Das Prinzip der virtuellen Verrückungen für elastische Körper besagt (ohne Herleitung)

i

a δA

δA = _{Gl. 8-1}

oder in Worten:

Befindet sich ein Körper im Gleichgewicht, dann ist bei einer virtuellen Verrückung des Körpers die Arbeit der äußeren Kräfte gleich der Arbeit der inneren Kräfte.

Werden bei der virtuellen Verrückung die Lagerungsbedingungen des Systems berück- sichtigt, dann kann statt δA auch _a δA_a^(e) (Arbeit der eingeprägten Kräfte¹) geschrieben werden, da dann die Reaktionskräfte bei der virtuellen Verrückung keine Arbeit leisten.

Es kann gezeigt werden (hier ohne Beweis), daß die Variation der inneren Arbeit iden- tisch ist mit der Variation der Formänderungsenergie, also δA_i =δW, so dass wir für Gl.

8-1 auch δA_a =δW oder umgeformt

(

)

δ δA

δW− _a = − _a ≡ = Gl. 8-2

schreiben können. Der Ausdruck

1 Die äußeren Kräfte setzen sich bekanntlich aus eingeprägten Kräften und Reaktionskräften zusammen

8-4 Das Prinzip der virtuellen Verrückung

) dO dV

ρ (

W A W Π

O(V) (V)

n

1 k

k m

1 j

j j

a

∑ ∑ ∫

∫

=

↓

=

↓ + + +

−

=

−

= F u M_kϕ fu s_Ou

wird elastisches Potential genannt, und Gl. 8-2 heißt Satz vom Extremum des elasti- schen Potentials.

In der obigen Gleichung wird im Ausdruck für die äußere Arbeit durch die aufgesetzten Pfeile angedeutet, daß allein die Verrückungsgrößen zu variieren sind. Das ist auch dann der Fall, wenn die Belastungen, z.B. bei Federkraftbelastungen, von den Verschiebungen abhängen. In Worten besagt Gl. 8-2:

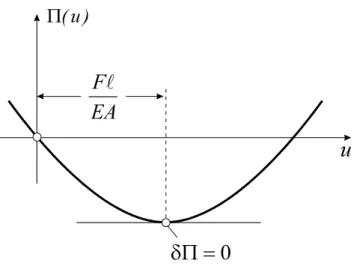
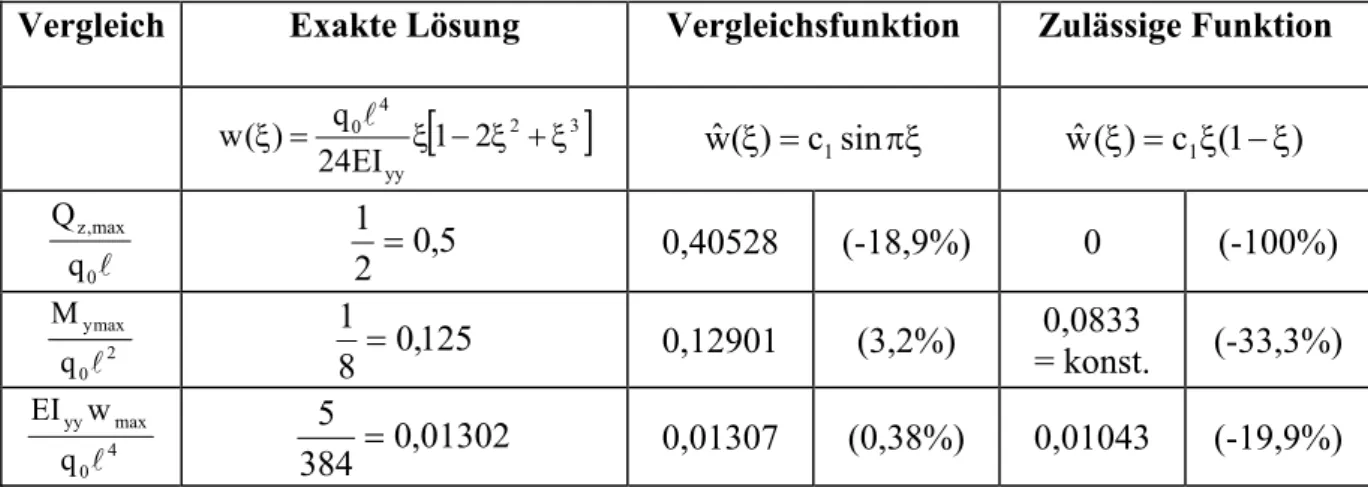
Von allen denkbaren Verschiebungszuständen eines elastischen Körpers ist Derjenige der wirklich Eintretende, für den die Energiegröße Π einen stationären Wert annimmt.

Abb. 8-2 Biegeträger mit Querbelastung

Ein Mittels des Prinzips der virtuellen Verrückung bereitgestelltes funktional unbestimm- tes Problem kann in eine Verschiebungsdifferentialgleichung übergeführt werden. Dazu betrachten wir den Biegeträger nach Abb. 8-2. Im Sinne des Prinzips muß der Ausdruck

dx ) x ( w ) x ( q ) x ( 2 w w EI

0 x

yy 2

∫

⎦

⎢ ⎤

⎣

⎡ ′′ −

>=

<

Π ^l Gl. 8-3

extremal gemacht werden. Das erfordert

[

]

0 x

yy ′′ δ ′′ − δ =

= Π

δ

∫

= l

Gl. 8-4

Die ansonsten beliebigen Verschiebungsvariationen δw(x) müssen an den Rändern die Bedingungen

0 ) ( w ) 0 (

w =δ =

δ l ^{Gl. 8-5}

erfüllen. Zur Einarbeitung der Randbedingungen wird Gl. 8-4 zweimal partiell integriert