Modeling and estimating income data in the presence of distinctive zero and heaped responses
Volltext
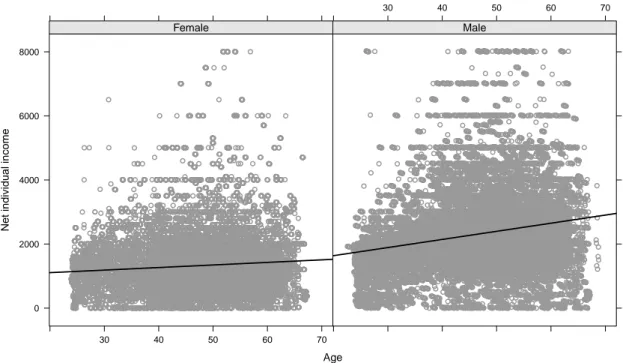
Abbildung
ÄHNLICHE DOKUMENTE
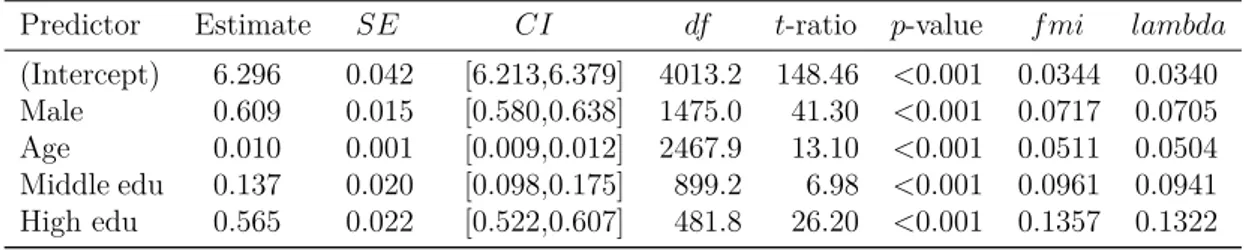
The algorithm computes an approximation of the Gaussian cumulative distribution function as defined in Equation (1). The values were calculated with the code taken
All the branch office has to do is mount a disk volume which has a copy of Datapoint's Disk Operating system and DATAPOLL on it and you can down line load
Three leading explanations are put forth for these cross-country differences: (1) other advanced economies devote a larger share of national output to transfers, which tends
4.1 LIS-Database - General characteristics and selected countries 8 4.2 Freelancers and self-employed: LIS data definitions 9 5 Income Distribution and Re-distribution in
based on the 1994 household survey. These tables yield the following importnt observations: 1) the share of wages and salaries in total income for the highest quintile was
Wage Policy in the Public Sector and Income Distribution.
For a constant price depreciation rate, both versions of the model would predict monotone relationships between mean household income and vehicle ownership statistics: a positive
For a constant price depreciation rate, both versions of the model would predict monotone relationships between mean household income and vehicle ownership statistics: a positive