Research Collection
Doctoral Thesis
Identification Results in Neural Network Theory and Linear Operator Theory
Author(s):
Vlacic, Verner Publication Date:
2021-03
Permanent Link:
https://doi.org/10.3929/ethz-b-000474903
Rights / License:
In Copyright - Non-Commercial Use Permitted
This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use.
IDENTIFICATION RESULTS IN NEURAL NETWORK THEORY AND
LINEAR OPERATOR THEORY
Verner Vlačić
DISS. ETH NO. 27318
IDENTIFICATION RESULTS IN NEURAL NETWORK THEORY AND
LINEAR OPERATOR THEORY
A thesis submitted to attain the degree of DOCTOR OF SCIENCES of ETH ZURICH
(Dr. sc. ETH Zurich)
presented by VERNER VLAČIĆ
MMath, University of Cambridge born on 27.11.1993
citizen of the Republic of Croatia and the Italian Republic
accepted on the recommendation of Prof. Dr. Helmut Bölcskei, examiner Prof. Dr. Afonso Bandeira, co-examiner Prof. Dr. Charles Fefferman, co-examiner
Mojim roditeljima, Vlasti i Ernestu
Abstract
This thesis addresses two distinct problems in the theory of system identification by means of various novel techniques relying on com- plex analysis. Specifically, we study the analytic continuation of deep neural networks with meromorphic nonlinearities, leading to a full resolution of the question posed in (Fefferman, 1994) of neural net- work identifiability for the tanh nonlinearity, and use the theory of interpolation and sampling of entire functions to derive necessary and sufficient conditions for the identifiability of linear time-varying (LTV) systems characterized by a (possibly infinite) discrete set of
delay-Doppler shifts.
The following question of neural network identifiability is the focus of the first part of the thesis: Suppose that we are given a function f :Rm→Rn and a nonlinearityρ. Can we specify the architecture, weights, and biases of all feed-forward neural networks with respect toρrealizingf? For the special case of the tanh nonlinearity, this question was first addressed in (Sussman, 1992) for single-layer net- works, and in (Fefferman, 1994) for multi-layer networks satisfying certain ‘genericity conditions’ on the architecture, weights, and biases.
The identifiability question for single-layer networks with nonlinear- ities satisfying the so-called ‘independence property’ was solved in (Albertini et al., 1993). In all these cases, the identified networks are mutually related by symmetries of the nonlinearity. For instance, the tanh function is odd, and so flipping the signs of the bias and the incoming and outgoing weights of a neuron does not change the Furthermore,output map of the network. In an effort to answer the identifiability question in greater generality, we consider arbitrary
show that the symmetries can be used to find a rich set of networks giving rise to the same functionf. The set obtained in this manner is, in fact, exhaustive (i.e., it contains all networks giving rise tof) if and only ifρsatisfies the so-callednull-net condition, i.e., there does not exist a network ‘with no internal symmetries’ giving rise to the identically zero function. This result can thus be interpreted as an analogue of the rank-nullity theorem for linear operators.
Furthermore, we derive sufficient conditions (termed thealignment conditions) on meromorphic nonlinearities with simple poles only that guarantee that the null-net condition holds, and we exhibit a class of ‘tanh-type’ nonlinearities (including the tanh function itself) satisfying the alignment conditions, thereby solving the identifiability question for these nonlinearities in full generality. Moreover, we do so for neural networks that may contain skip connections. The alignment conditions, although rather technical, are statements about linear combinations of functions, unlike the original identifiability question and the null-net condition, which are ‘recursive’ statements aboutρ (i.e., statements about repeated compositions of affine functions and ρ). The significance of the alignment conditions thus lies in bridging the conceptual gap between the identifiability of single-layer networks and multi-layer networks, at least for meromorphic nonlinearities with simple poles only.
Finally, we consider a class of meromorphic nonlinearities for which we do not verify the alignment conditions (and, indeed, we hold this task to be impractical), and yet we are able to verify the null- net condition for these nonlinearities directly, although in this case the result holds only for layered neural networks (i.e., with no skip connections).
The second part of the thesis deals with the problem of identifying a linear time-varying (LTV) system, which has been a topic of long- standing interest, dating back to the seminal work (Kailath, 1962;
Bello, 1969), and has seen significant renewed interest during the past decade (Kozek and Pfander, 2005; Heckel and Bölcskei, 2013;
Bajwa et al., 2011; Heckel et al., 2014). In this thesis, we consider
LTV systems characterized by a (possibly infinite) discrete set of delay-Doppler shifts and show that a class of such LTV systems is identifiable whenever the upper uniform (over the class) Beurling density of the delay-Doppler support sets is strictly less than 1/2. The proof of this result relies on the theory of interpolation and sampling in the Bargmann-Fock space of entire functions. Moreover, we show that this density condition is also necessary for the identifiability of classes of systems invariant under time-frequency shifts and closed in a natural topology. Finally, we show that identifiability guarantees robust recovery of the geometry of the delay-Doppler support set, as well as the weights of the individual delay-Doppler shifts. Unlike previous results of this kind, ours does not assume a lattice constraint on the support sets.
Kurzfassung
Diese Dissertation behandelt zwei verschiedene Probleme in der The- orie der Systemidentifikation unter Verwendung neuartiger mathema- tischer Techniken aus dem Gebiet der komplexen Analysis. Im ersten Teil der Arbeit betrachten wir die analytische Fortsetzung tiefer neu- ronaler Netzwerke (engl. deep neural networks), was zur Lösung der in (Fefferman, 1994) gestellten Frage der Identifizierbarkeit neuronaler Netzwerke führt. Im zweiten Teil benutzen wir die Interpolations–
und Abtastungstheorie für ganze Funktionen um notwendige und hin- reichende Bedingungen für die Identifizierbarkeit linearer zeitlich vari- ierender Systeme, die durch eine (möglicherweise unendliche) Menge Delay-Doppler-Verschiebungen charakterisiert sind, abzuleiten.
Die folgende Frage der Identifizierbarkeit für neuronale Netzwerke steht im Fokus des ersten Teils der Dissertation: Es seien eine Funk- tion f : Rm →Rn und eine Nichtlinearität ρgegeben. Kann man die Architektur, die Gewichte (engl. weights) und die Schwellwerte (engl. biases) aller neuronalen Netzwerke bestimmen, die mit der Nichtlinearitätρdie Funktionf realisieren? Für den Spezialfall der Nichtlinearitätρ= tanh wurde diese Frage in (Sussman, 1992) für einschichtige Netzwerke und in (Fefferman, 1994) für mehrschichtige Netzwerke, die gewisse «generische Bedingungen» erfüllen, behandelt.
Die Identifizierbarkeitsfrage für einschichtige Netzwerke mit Nichtlin- earitäten, die die sogenannte «Unabhängigkeitseigenschaft» haben, wurde in (Albertini et al., 1993) gelöst. In allen oben genannten Fällen sind die identifizierten Netzwerke durch Symmetrien der Nichtlinear- ität verbunden. Ein Bespiel dafür ist die ungerade tanh-Nichtlinearität, bei der man die Vorzeichen der Schwellwerte und der eingehenden
die Outputfunktion des Netzwerks zu verändern.
Im Bemühen die Identifizierbarkeitsfrage in grösserer Allgemein- heit zu beantworten, betrachten wir beliebige Nichtlinearitäten mit möglicherweise komplizierten affinen Symmetrien und zeigen dafür, dass die Symmetrien erlauben, eine reiche Menge an Netzwerken, die dieselbe Funktionf realisieren, zu finden. Die so erhaltene Menge ist tatsächlich vollständig (d.h., sie beinhaltet alle Netzwerke dief real- isieren) dann und nur dann, wennρdie sogenannteNullnetzbedingung erfüllt, d.h., es gibt kein Netzwerk «ohne interne Symmetrien», welches die Nullfunktion realisiert. Damit kann man dieses Ergebnis als ein Analogon des Rangsatzes für lineare Abbildungen interpretieren.
Darüber hinaus leiten wir hinreichende Bedingungen (die sogenan- ntenAusrichtungsbedingungen) für meromorphe Nichtlinearitäten mit Polen der Ordnung 1 ab, die sicherstellen, dass die Nullnetzbedingung erfüllt ist. Ebenso präsentieren wir eine Klasse «tanh-ähnlicher» Nicht- linearitäten (einschliesslich der Funktion tanh selbst), welche die Aus- richtungsbedingungen erfüllen. Dies löst die Identifizierbarkeitsfrage für diese Nichtlinearitäten in voller Allgemeinheit. Unsere Ergeb- nisse sind auch für Netzwerke mit sogenannten Skipverbindungen gültig. Obwohl die Ausrichtungsbedingungen technischer Natur sind, stellen sie Annahmen über lineare Kombinationen der Funktionen dar, im Gegensatz zur ursprünglichen Identifizierbarkeitsfrage und der Nullnetzbedingung, die «rekursive» Annahmen überρsind. Die Bedeutung der Ausrichtungsbedingungen liegt deshalb in der Über- brückung der konzeptionellen Lücke zwischen der Identifizierbarkeit für einschichtige und für mehrschichtige Netzwerke, zumindest für meromorphe Nichtlinearitäten mit Polen der Ordnung 1.
Schliesslich betrachten wir eine Klasse meromorpher Nichtlinear- itäten, für die wir die Ausrichtungsbedingungen nicht überprüfen (und zwar halten wir das für nicht praktikabel). Dennoch sind wir in der Lage die Nullnetzbedingung für diese Nichtlinearitäten direkt zu verifizieren, obwohl das Ergebnis nun nur für geschichtete Netzwerke (d.h., ohne Skipverbindungen) gilt.
Der zweite Teil der Dissertation behandelt das Problem der Iden-
tifikation eines linearen zeitlich veränderlichen (engl. linear time- varying, LTV) Systems. Dieses Thema, das auf die bahnbrechen- den Arbeiten (Kailath, 1962; Bello, 1969) zurückgeht, hat im let- zten Jahrzehnt bedeutendes erneuertes Interesse erfahren (Kozek and Pfander, 2005; Heckel and Bölcskei, 2013; Bajwa et al., 2011;
Heckel et al., 2014). In der vorliegenden Dissertation betrachten wir LTV Systeme, die durch eine (möglicherweise unendliche) Menge von Delay-Doppler-Verschiebungen charakterisiert sind, und beweisen, dass solche LTV Systeme identifizierbar sind, sobald die obere gle- ichmässige (über die Klasse) gemessene Beurlingdichte der Delay- Doppler-Trägermengen streng kleiner als 1/2 ist. Der Beweis dieses Ergebnisses beruht auf der Interpolations– und Abtastungstheorie für ganze Funktionen im Bargmann-Fock-Raum. Des Weiteren zeigen wir, dass unsere Dichtebedingung für die Identifizierbarkeit von Systemen, die unter Zeit-Frequenz-Verschiebungen invariant und in einer natür- lichen Topologie geschlossen sind, auch notwendig ist. Schliesslich zeigen wir, dass Identifizierbarkeit eine robuste Wiedergewinnung sowohl der Geometrie der Delay-Doppler-Trägermenge als auch der zugehörigen Gewichte der einzelnen Delay-Doppler-Verschiebungen garantiert. Im Gegensatz zu früheren Ergebnissen dieser Art setzen unsere Ergebnisse keine Gittereinschränkung für die Delay-Doppler- Trägermenge voraus.
Sommario
Questa tesi affronta due problemi diversi nella teoria di identificazione del sistema tramite varie nuove tecniche che si basano su analisi complesse. Specificamente, si studia il prolungamento analitico di reti neurali profonde con non-linearità meromorfe, portando alla completa risoluzione della questione posta in (Fefferman, 1994) della identificabilità delle reti neurali con la non-linearità tanh, e si utilizza la teoria dell’interpolazione e del campionamento di funzioni intere per derivare le condizioni necessarie e sufficienti per l’identificabilità di sistemi lineari variabili nel tempo (ingl. LTV) caratterizzati da un insieme discreto (e possibilmente infinito) di spostamenti delay- Doppler.
La seguente questione della identificabilità di reti neurali è al centro della prima parte della tesi: Siano date una funzione f :Rm→Rn e una non-linearità ρ. È possibile specificare l’architettura, i pesi (ingl. weights) e le soglie (ingl. biases) di tutte le reti neurali con la non-linearità ρ che realizzano f? Per il caso speciale della non- linearità tanh, questa domanda è stata affrontata per la prima volta in (Sussman, 1992) per le reti a strato singolo, e in (Fefferman, 1994) per le reti multistrati che soddisfano certe «condizioni di genericità».
La questione della identificabilità per reti a strato singolo con non- linearità che hanno la cosiddetta «proprietà di indipendenza» è stata risolta in (Albertini et al., 1993). In tutti questi casi, le reti identificate sono reciprocamente correlate dalle simmetrie della non-linearità. Ad esempio, la funzione tanh è dispari, quindi cambiare i segni della soglia e dei pesi entranti e uscenti di un neurone non cambia la funzione di output della rete. Nel tentativo di rispondere alla questione della
arbitrarie con simmetrie affini potenzialmente complicate e mostriamo che le simmetrie possono essere utilizzate per trovare un ricco insieme di reti che realizzano la stessa funzionef. L’insieme così ottenuto è infatti esaustivo (cioè contiene tutte le reti che realizzanof) se e solo seρsoddisfa la cosiddettacondizione di rete nulla, ovvero non esiste una rete «senza simmetrie interne» che realizza la funzione nulla.
Questo risultato può quindi essere interpretato come un analogo del teorema del rango per trasformazioni lineari.
Inoltre, deriviamo delle condizioni sufficienti (chiamatecondizioni di allineamento) su non-linearità meromorfe soltanto con poli di ordine 1 che garantiscono che la condizione di rete nulla valga, e mostriamo una classe di alcune non-linearità di «tipotanh» (tra cui la stessa funzione tanh) che soddisfano le condizioni di allineamento, risol- vendo così la questione della identificabilità per queste non linearità in piena generalità. In aggiunta, lo facciamo per reti neurali che pos- sono contenere delle connessioni skip. Le condizioni di allineamento, sebbene piuttosto tecniche, sono proposizioni su combinazioni lineari di funzioni, al contrario della questione originale della identificabilità e della condizione di rete nulla, che sono proposizioni «ricorsive» suρ (cioè, proposizioni su composizioni ripetute di funzioni affini e delρ).
Il significato delle condizioni di allineamento sta quindi nel colmare il divario tra l’identificabilità delle reti a strato singolo e l’identificabilità delle reti multistrati, almeno per le non-linearità meromorfe soltanto con poli di ordine 1.
Infine, consideriamo una classe di alcune non-linearità meromorfe per le quali non verifichiamo le condizioni di allineamento (anzi riteniamo che questo compito sia impraticabile), e tuttavia riusciamo a verificare direttamente la condizione di rete nulla per queste non- linearità, sebbene in questo caso il risultato valga solo per le reti neurali stratificate (cioè, senza connessioni skip).
La seconda parte della tesi affronta il problema della identificazione di un sistema lineare variabile nel tempo (ingl. LTV), che è stato un tema di interesse di lunga data, risalente ai lavori seminali (Kailath, 1962; Bello, 1969) e ha ricevuto un interesse rinnovato negli ultimi
dieci anni (Kozek and Pfander, 2005; Heckel and Bölcskei, 2013; Bajwa et al., 2011; Heckel et al., 2014). In questa tesi consideriamo sistemi LTV caratterizzati da un insieme discreto (e possibilmente infinito) di spostamenti delay-Doppler. Mostriamo che una classe di tali sistemi LTV è identificabile qualora la densità Beurling superiore degli insiemi dei supporti delay-Doppler, misurata uniformemente sulla classe, sia strettamente minore di 1/2. La dimostrazione di questo risultato si basa sulla teoria dell’interpolazione e del campionamento nello spazio di Bargmann-Fock di funzioni intere. Inoltre, mostriamo che questa condizione di densità è anche necessaria per l’identificabilità di classi di sistemi invarianti sotto spostamenti tempo-frequenza e chiusi in una topologia naturale. Infine, dimostriamo che l’identificabilità garantisce un ricupero robusto della geometria dell’insieme dei supporti delay- Doppler, così come dei pesi dei singoli spostamenti delay-Doppler.
A differenza dei precedenti risultati di questo tipo, il nostro non presuppone un vincolo reticolare sugli insiemi dei supporti.
Acknowledgments
Firstly, I wish to express my deepest gratitude to my advisor, Prof.
Helmut Bölcskei, for his excellent guidance throughout my doctoral studies, and for the freedom and support I enjoyed in pursuing topics beside my thesis. Helmut’s commitment to detail and emphasis on the clarity of expression are truly exceptional, and have inspired me to strive for perfection in my own writing.
I am grateful to professors Afonso Bandeira, Helmut Bölcskei, and Charles Fefferman for acting as examiners for this thesis.
Alexander Bastounis and Anders Hansen deserve special mention for their dedication to our colossal project that has spanned my doc- toral studies and brought welcome variety into my research. I am also indebted to Thomas Allard, Céline Aubel, and Charles Fefferman for many inspiring discussions and contributions that were valuable for the outcome of my work.
I would like to thank my friends and colleagues from ETHZ and Cambridge for being there for me. I will always remember the en- joyable times we shared and the environment of inspiration and motivation you provided.
Finally, my warmest thanks go to my parents Vlasta and Ernest for their unrelenting love, encouragement, and support over the years.
Contents
1 Introduction 1
1.1 Neural network identifiability . . . . 1 1.2 Identifiability criteria for linear time-varying systems . 5 1.2.1 Fundamental limits on identifiability . . . . 7 1.2.2 Robust recovery of the delay-Doppler support set 9 1.3 Publications . . . . 10
2 Neural network identifiability 11
2.1 A theory of identifiability based on affine symmetries . 21 2.1.1 Absence of the null-net condition for the ReLU 27 2.2 Identifiability for the tanh and the alignment conditions 28 2.2.1 Single-layer networks and the SAC . . . . 28 2.2.2 Multi-layer networks and the CAC . . . . 31 2.2.3 General meromorphic nonlinearities and arbi-
trary input sets . . . . 37 2.2.4 The class Σa,b of nonlinearities . . . . 39 2.3 Identifiability for generic meromorphic nonlinearities . 41 2.4 Theρ-isomorphism and the null-net theorems . . . . . 44 2.5 Pole clustering for single-input network maps . . . . . 57 2.6 Input anchoring . . . . 68 2.6.1 Proof of Theorem 2.3 . . . . 76 2.7 The alignment conditions for Σa,b-nonlinearities . . . . 76 2.7.1 Asymptotic density and the CAC . . . . 77 2.7.2 The SAC for Σa,b-nonlinearities . . . . 85 2.8 Kronecker’s theorem and input splitting . . . . 88 Appendices . . . 110
2.A Proofs of Proposition 2.3 and Lemma 2.3 . . . 110 2.B Proofs of auxiliary results in Section 2.4 . . . 112 2.C Proofs of auxiliary results in Section 2.5 . . . 120 2.D Proof of Lemma 2.9 . . . 123 2.E Proofs of auxiliary results in Section 2.7 . . . 125 2.F Proofs of auxiliary results in Section 2.8 . . . 132 3 Identifiability of linear time-varying systems 141 3.1 Overview of the main results . . . 143
3.1.1 A necessary and sufficient condition for identi- fiability . . . 145 3.1.2 Identifiability and robust recovery . . . 148 3.1.3 Examples of identifiable and non-identifiable
regular classes . . . 150 3.2 Lattices, Beurling densities, and Wiener amalgam spaces151 3.3 Proof of Theorem 3.1 . . . 155 3.4 Proof of Theorem 3.2 . . . 163 3.5 Proofs of Theorems 3.3 and 3.4 . . . 166 3.6 Proofs of Proposition 3.2 and Corollaries 3.1, 3.2, and
3.3 . . . 176 Appendices . . . 178 3.A Proof of Propositon 3.1 . . . 178 3.B Proof of auxiliary results in Section 3.2 . . . 180 3.C Proof of Lemma 3.5 . . . 182 3.D Proofs of Lemmas 3.6, 3.7, and 3.8 . . . 194
References 197
CHAPTER 1
Introduction
The thesis consists of two standalone parts, each dealing with a different problem in the theory of system identification. The first part builds a theory of neural network identifiability, and the second addresses the identifiability of linear time-varying (LTV) delay-doppler systems.
1.1. NEURAL NETWORK IDENTIFIABILITY
Deep neural network learning has become a highly successful machine learning method employed in a wide range of applications such as optical character recognition (LeCun et al., 1995), image classification (Krizhevsky et al., 2012), speech recognition (Hinton et al., 2012), and generative models (Goodfellow et al., 2014). Neural networks are typically defined as concatenations of affine maps between finite dimensional spaces and nonlinearities applied elementwise, and are often studied as mathematical objects in their own right, for instance in approximation theory (Bölcskei et al., 2019; Mallat, 2012; Petersen and Voigtländer, 2018; Wiatowski and Bölcskei, 2018) and in control theory (Albertini and Sontag, 1993a,b).
In data-driven applications (Goodfellow et al., 2016; LeCun et al., 2015) the parameters of a neural network (i.e., the coefficients of the network’s affine maps) need to be learned based on training data.
In many cases, however, there exist multiple networks with different parameters, or even different architectures, giving rise to the same
input-output map on the training set. These networks might differ, however, in terms of their generalization performance. In fact, even if several networks with differing architectures realize the same map on the entire domain, some of them might be easier to arrive at through training than others. It is therefore of interest to understand the ways in which a given function can be parametrized as a neural network.
Specifically, we ask the following question of identifiability: Suppose that we are given a function f : Rm → Rn and a nonlinearity ρ.
Can we specify the network architecture, weights, and biases of all feed-forward neural networks with respect toρrealizingf? For the special case of the tanh nonlinearity, this question was first addressed in (Sussman, 1992) for single-layer networks, and in (Fefferman, 1994) for multi-layer networks satisfying certain ‘genericity conditions’ on the architecture, weights, and biases. The identifiability question for single-layer networks with nonlinearities satisfying the so-called
‘independence property’ was solved in (Albertini et al., 1993). We also remark that the identifiability of recurrent single-layer networks was considered in (Albertini and Sontag, 1993a) and (Albertini and Sontag, 1993b).
It is important to note that all aforementioned results, as well as the results presented in the thesis, are concerned with the identifi- ability of networks given knowledge of the functionf on its entire domain. This corresponds to characterizing the fundamental limit on nonuniqueness in neural network representation of functions. Specif- ically, the nonuniqueness can only be richer if we are interested in networks that realizef on a proper subset of Rm, such as a finite (training) sample{x1, . . . , xm} ⊂Rm. Moreover, we do not address neural network reconstruction, i.e., we do not provide a procedure for constructing an instance of a network realizing a given functionf, but rather focus on building a theory that systematically describes how the neural networks realizingf relate to one another. We do this in full generality for networks with ‘tanh-type’ nonlinearities (including the tanh function itself), settling an open problem posed by Fefferman in (Fefferman, 1994).
Recent results on neural network reconstruction on samples can be
1.1 NEURAL NETWORK IDENTIFIABILITY
found in (Fornasier et al., 2018), (Fornasier et al., 2019) for shallow networks and in (Rolnick and Kording, 2020) for ReLU networks of arbitrary depth.
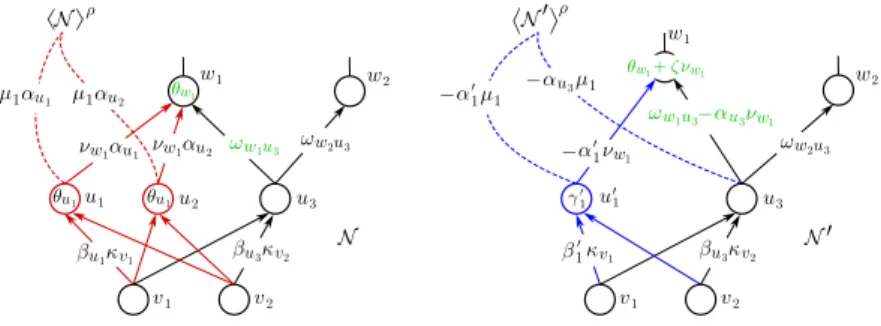
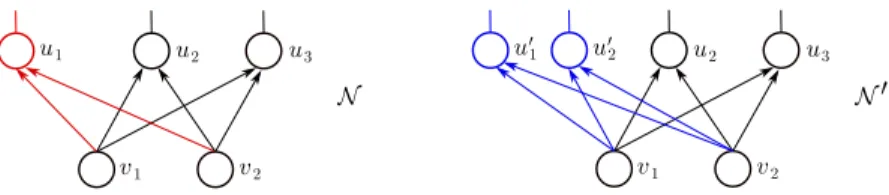
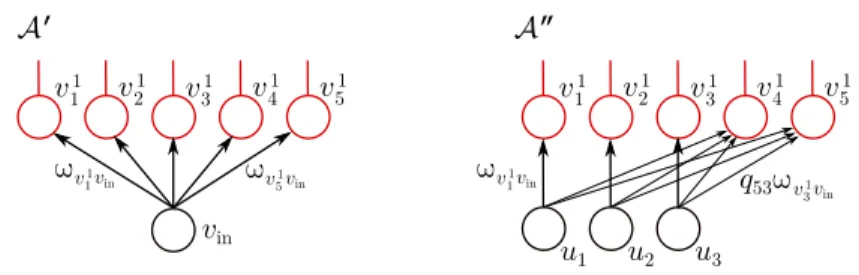
In this part of the thesis, we build a general theory of neural network identifiability based on affine symmetries. An affine symmetry (formalized in Definition 2.1) of a nonlinearity ρcan be informally described as a collection of affine mapsA1, . . . , An :R→Rsuch that {ρ◦A1, . . . , ρ◦An,1}is a linearly dependent set of functions onR, where 1:R→Rdenotes the constant function taking on the value 1.
It will follow immediately that non-uniqueness in the realization of a function as a single-layer neural network with nonlinearityρstands in direct correspondence with the affine symmetries ofρ, and moreover, we will see how affine symmetries lead in a canonical fashion (i.e., by means ofρ-modification) to different multi-layer networks realizing the same function.
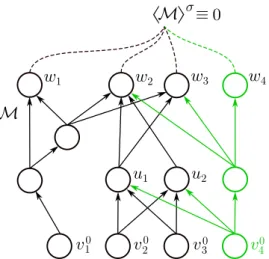
The first main contribution of the thesis are the null-net theorems, which establish a necessary and sufficient condition, termed the null- net condition, for the set networks obtained throughρ-modification to be exhaustive, i.e., to contain all networks realizing a given function, thereby settling the identifiability question in the positive. Specifically, ρis said to satisfy the null-net condition if there does not exist a network ‘with no internal symmetries’ giving rise to the identically zero function. The theory is simultaneously developed for layered neural networks (i.e., with no skip connections) and for general neural networks (i.e., possibly containing skip connections), and consequently there are two null-net theorems. Even though both identifiability and the null-net condition are statements quantified over all neural networks, and in particular over networks of arbitrarily complicated architecture, the null-net theorems allow us to shift the original question of identifiability to a different realm where the problem will be easier to tackle by leveraging the ‘fine properties’ of the nonlinearity.
We will additionally see how these results can thus be interpreted as analogues of the rank-nullity theorem for linear operators.
Our goal will henceforth be to establish suitable sufficient condi- tions on nonlinearities guaranteeing that the null-net condition holds.
To this end, we will first motivate our results and techniques by demonstrating informally how the null-net condition is established for the tanh nonlinearity and for neural networks with 1-dimensional input (possibly containing skip connections). As the maps realized by such networks are functions of one variable, and are defined in terms of repeated compositions of the meromorphic function tanh and affine combinations, they can be analytically continued to their natural domains inCand can therefore be studied in the context of complex analysis. This approach was pioneered in (Fefferman, 1994).
This discussion will reveal a sufficient condition (the alignment con- ditions) for the argument for the tanh nonlinearity to generalize to arbitrary meromorphic nonlinearities with simple poles only, albeit still for neural networks with 1-dimensional input only. The final step is to establish the null-net property for neural networks with inputs of arbitrary dimension. This will be achieved by means of the so-called input anchoring procedure, which is a method for reducing the dimension of the input of a neural network by setting some of the input coordinates to fixed values and deleting the parts of the network that are rendered constant in the process.
The alignment conditions are admittedly rather technical condi- tions. However, unlike the null-net condition, which is a ‘recursive’
statement about the nonlinearity (i.e., a statement about repeated compositions of affine functions andσ), the alignment conditions are statements about linear combinations of functions. Their significance thus lies in bridging the conceptual gap between the identifiability of single-layer networks and the identifiability of multi-layer networks, at least for meromorphic nonlinearities with simple poles only. We will use various ‘point density’ techniques (such as the Kronecker- Weyl equidistribution theorem) to verify the alignment conditions for nonlinearities of the form
σ=C+X
k∈Z
ck
sgn(k) + tanh πb−1(· −ka) ,
wherea, b >0,C∈C, and{ck}k∈Zis a sequence of complex numbers
1.2 IDENTIFIABILITY CRITERIA FOR LINEAR TIME-VARYING SYSTEMS
such that supk∈Z|ck|e−πa0|k|/b<∞, for somea0∈(0, a), and at least oneck is nonzero.
Finally, we will exhibit a class of meromorphic nonlinearities with simple poles only for which we do not verify the alignment conditions (and, indeed, we hold this task to be impractical), and yet we are able to verify the null-net condition for these nonlinearities directly. This is achieved by a technique termed input splitting, which combines Kronecker’s theorem Kronecker (1979) and analytic continuation to
‘simulate’ a neural network with multi-dimensional input by means of a network with 1-dimensional input.
We conclude with an overview of the first part of the thesis. Sections 2.1, 2.2, and 2.3 are informal and introduce the null-net theorems, the alignment conditions and input anchoring, and input splitting, respectively. The goal of these sections is to motivate the theory at a steady pace and in a logical order, without digressing into the technicalities behind the formal proofs of the results. The theory is then formalized and the results proved rigorously in the remaining sections of Chapter 2. Finally, the appendices contain the proofs of various results that are either simple, standard, or based on ideas already seen in the main body of the chapter.
1.2. IDENTIFIABILITY CRITERIA FOR LINEAR TIME-VARYING SYSTEMS
Identification of deterministic linear time-varying (LTV) systems has been a topic of long-standing interest, dating back to the seminal work Kailath (1962) and Bello (1969), and has seen significant renewed interest during the past decade, see Kozek and Pfander (2005); Heckel and Bölcskei (2013); Bajwa et al. (2011); Heckel et al. (2014). The identification of a deterministic linear operator from the operator’s response to a probing signal is an important problem in many fields of engineering. Concrete examples include system identification in control theory and practice, the measurement of dispersive communication channels, and radar imaging. The formal problem statement is as
follows: We wish to identify the LTV systemHfrom its response (Hx)(t) :=
Z
R2
SH(τ, ν)x(t−τ)e2πiνtdτdν, ∀t∈R, (1.1) to a probing signalx(t), withSH(τ, ν) denoting the spreading function associated with the operator. The representation theorem (Gröchenig, 2000, Thm. 14.3.5) states that a large class of continuous linear operators can be represented as in (1.1). Kailath (1962) showed that an LTV system with spreading function supported on a rectangle in the (τ, ν)-plane is identifiable if the area of the rectangle is at most 1.
This result was later extended in Bello (1969) to arbitrarily fragmented spreading function support regions with the support area measured collectively over all supporting pieces. Necessity of the Kailath-Bello condition was established in Kozek and Pfander (2005); Pfander and Walnut (2006) through elegant functional-analytic arguments.
However, all these results require the support region ofSH(τ, ν) to be known prior to identification, a condition that is very restrictive and often impossible to realize in practice. More recently, it was demonstrated by Heckel and Bölcskei (2013) that identifiability is possible without prior knowledge of the operator’s spreading function support region and without limitations on its total extent, again for spreading function support regions of area (measured collectively over all supporting pieces) upper-bounded by 1. This result is surprising as it says that there is no price to be paid for not knowing the spreading function’s support region in advance. This insight has strong conceptual ties to the theory of spectrum-blind sampling of sparse multi-band signals, see Feng and Bresler (1996); Feng (1997);
Lu and Do (2008); Mishali and Eldar (2009).
The situation is fundamentally different when the spreading function is discrete according to
(Hx)(t) := X
m∈N
αmx(t−τm)e2πiνmt, ∀t∈R, (1.2) where (τm, νm)∈R2 are delay-Doppler shift parameters andαm are
1.2 IDENTIFIABILITY CRITERIA FOR LINEAR TIME-VARYING SYSTEMS
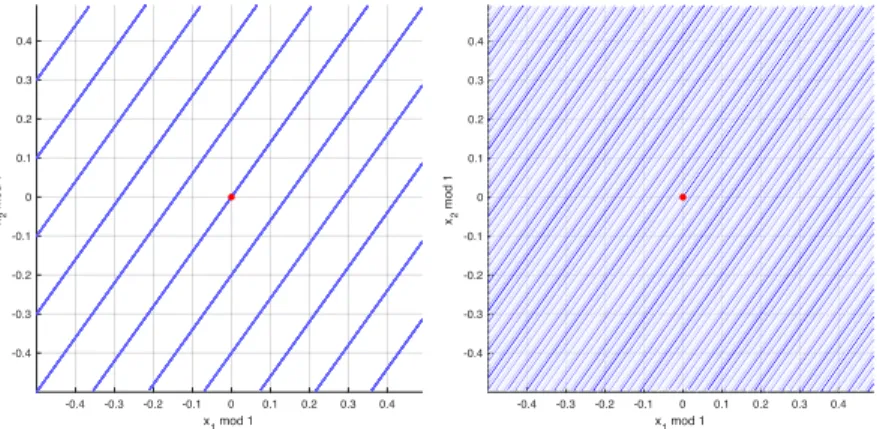
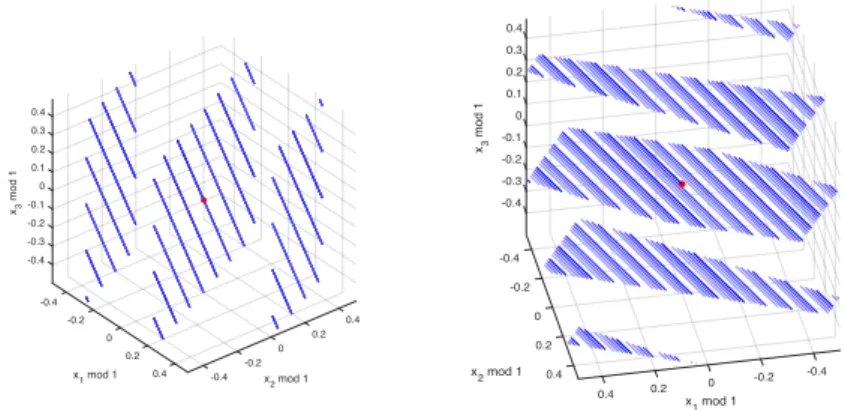
the corresponding complex weights, form∈N. Here, the (discrete) spreading function can be supported on unbounded subsets of the (τ, ν)-plane with the identifiability condition on the support area of the spreading function replaced by a density condition on the support set supp(H) :={(τm, νm) :m∈N}. Specifically, for rectangular lattices supp(H) =a−1Z×b−1Z, Kozek and Pfander (2005) established that His identifiable if and only ifab≤1. In Grip et al. (2013) a necessary condition for identifiability of a set of Hilbert-Schmidt operators defined analogously to (1.2) is given; the condition is expressed in terms of a the Beurling density of the support sets, but the time- frequency pairs (τ, ν) are assumed to be confined to a lattice. Now, in practice the discrete spreading function will not be supported on a lattice as the parametersτ, ν correspond to time-delays and frequency shifts induced, e.g. in wireless communication, by the propagation environment. It is hence of interest to understand the limits on identifiability in the absence of ‘geometry-discretizing’ assumptions, such as a lattice constraint, on supp(H). Resolving this problem is the aim of this thesis chapter.
1.2.1. Fundamental limits on identifiability
The purpose of this thesis chapter is twofold. First, we establish fundamental limits on the stable identifiability ofHin (1.2) in terms of supp(H) and{αm}m∈N. Our approach is based on the following insight. Defining the discrete complex measureµ:=P
m∈Nαmδτm,νm
onR2, where δτm,νm denotes the Dirac delta function with mass at (τm, νm), the input-output relation (1.2) can be formally rewritten as
(Hµx)(t) = Z
R2
x(t−τ)e2πiνtdµ(τ, ν), t∈R, (1.3) where we write Hµ instead of H for concreteness. Identifying the system Hµ thus amounts to reconstructing the discrete measure µ fromHµx. More specifically, we wish to find necessary and sufficient conditions on classesHof measures guaranteeing stable identifiability
bounds of the form
dr(µ, µ0)≤dm(Hµx,Hµ0x), for allµ, µ0∈H, (1.4) for appropriate reconstruction and measurement metricsdranddm, whereµ is the ground truth measure to be recovered andµ0 is the estimated measure. The class Hcan be thought of as modelling the prior information known about the measure µ facilitating its identification by restricting the set of potential estimated measures µ0. In particular, the smaller the classH, the ‘easier’ it is to satisfy (1.4). In addition to the class of measures itself, the existence of a bound of the form (1.4) depends on the choice of the probing signal x, so we will later speak ofidentifiability byx.
This formulation reveals an interesting connection to the super- resolution problem as studied by Donoho (1992), where the goal is to recover a discrete complex measure onR, i.e., a weighted Dirac train, from low-pass measurements. The problem at hand, albeit formally similar, differs in several important aspects. First, we want to identify a measureµonR2, i.e., a measure on atwo-dimensional set, from observations inoneparameter, namelyHµx. Next, the low- pass observations in Donoho (1992) are replaced by short-time Fourier transform-type observations, where the probing signalxappears as the window function. While super-resolution from STFT-measurements was considered in Aubel et al. (2017), the underlying measure to be identified in Aubel et al. (2017) is, as in Donoho (1992), onR. Finally, Donoho (1992) assumes that the support sets of the measures under consideration are confined to an a priori fixed lattice. While such a strong structural assumption allows for the reconstruction metricdr to take a simple and intuitive form, it unfortunately bars any discussion of the geometric properties of the support sets. By contrast, our definition of stable identifiability will pave the way for a theory of support recovery without a lattice assumption discussed in the next subsection.
These differences make for very different technical challenges. Nev- ertheless, we can follow the spirit of Donoho (1992), where necessary
1.2 IDENTIFIABILITY CRITERIA FOR LINEAR TIME-VARYING SYSTEMS
and sufficient conditions were established for stable identifiability in the classical super-resolution problem. These conditions are ex- pressed in terms of the uniform Beurling density of the measure’s (one-dimensional) support set and are derived using density theorems for interpolation in the Bernstein and Paley-Wiener spaces (see Beurl- ing (1989b)) and for the balayage of Fourier-Stieltjes transforms (see Beurling (1989a)). We will, likewise, establish a sufficient condition for stable recovery, which states that stable identifiability is possible for classes of measures whose supports have density less than 1/2
‘uniformly over the classH’ (to be formally introduced in Definition 3.2). In addition, we show that this is also a necessary condition for classes of measures invariant under time-frequency shifts and closed under a natural topology on the support sets. We will see below that these conditions are not very restrictive as we present several examples of identifiable and non-identifiable classes of measures. The proofs of these results are based on the density theorem for interpolation in the Bargmann-Fock space (see Seip (1992a,b,c); Brekke and Seip (1993)), as well as several results about Riesz sequences from Gröchenig et al.
(2015).
1.2.2. Robust recovery of the delay-Doppler support set
The second goal of the paper is to address the implications of the identifiability condition on the recovery of the discrete measureµ.
Concretely, suppose that we want to recover a fixed measureµ :=
P
m∈Nαmδτm,νm from a known class of measuresHassumed to be stably identifiable (in the sense of (1.4)) with respect to a probing signalx, and let{µn}n∈N⊂Hbe a sequence of ‘candidate measures’
µn:=P
m∈Nα(n)m δτ(n)
m ,ν(n)m for the recovery ofµ. We will show that, under a mild regularity condition on x, the stable identifiability condition (1.4) on Hguarantees that
Hµnx→ Hµx =⇒ supp(Hµn)→supp(Hµ) and
{α(n)m }m∈N→ {αm}m∈N, (1.5)
as n → ∞, where the topologies in which these limits take place will be specified in due course. In words, this result says that the better the measurements with respect to the estimated measure match the true measurements, the closer the estimated measure is to the ground truth. This, in particular, shows that ‘measurement matching’ is sufficient for recovery within identifiable classesH, i.e., any algorithm that generates a sequence of measures{µn}n∈N⊂H satisfyingHµnx→ Hµxwill succeed in recoveringµ∈H. Crucially, we do not assume that the support sets supp(Hµ) and supp(Hµn), for n ∈ N, are confined to a lattice (or any other a priori fixed discrete set). To the best of our knowledge, this is the first known LTV identification result on the robust recovery of the support set of the measure, instead of its weights only.
The second part of the thesis is structured as follows. In Section 3.1, the main results are presented in a streamlined but rigorous fashion.
Next, Section 3.2 introduces additional standard technical concepts in time-frequency analysis that are needed in many of the proofs.
Finally, the remaining sections and the appendices bring the formal proofs of the results of Chapter 3.
1.3. PUBLICATIONS
The results in Chapter 2 have been accepted for publication in (Vlačić and Bölcskei, 2020a,b), and the results in Chapter 3 can be found in (Vlačić et al., 2020).
CHAPTER 2
Neural network identifiability
In order to develop intuition on the identifiability of general neural networks, we follow (Sussman, 1992) and (Albertini et al., 1993) and begin by considering single-layer networks. To this end, letρ:R→R be a nonlinearity, and let
hN iρ:=
n
X
p=1
λpρ(ωp· +θp) +λ and
hN0iρ:=
n0
X
p=1
λ0pρ(ω0p· +θp0) +λ0
(2.1)
be the maps realized by the single-layer networksN andN0, both with nonlinearity ρ. Suppose that these networks realize the same function, i.e.,
n
X
p=1
λpρ(ωpt+θp) +λ=
n0
X
p=1
λ0pρ(ω0pt+θp0) +λ0,
for allt∈R. This is equivalent to the following linear dependency relation between the constant function1:R→Rtaking on the value 1 and affinely transformed copies ofρ:
n
X
p=1
λpρ(ωpt+θp) −
n0
X
p=1
λ0pρ(ω0pt+θp0) = (λ0−λ)1(t), (2.2)
for allt∈R.
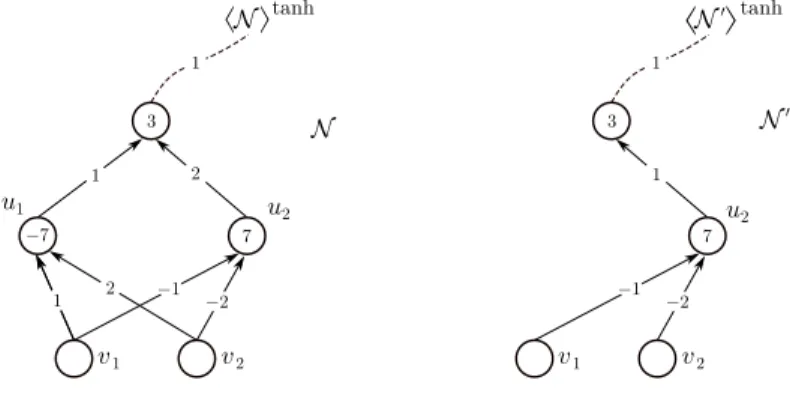
We consider two concrete nonlinearities to demonstrate how linear dependency relations of the form (2.2) lead to formally different networks realizing the same function. First, letρ= tanh. Then, as tanh(t) =−tanh(−t), for allt∈R, we have
n
X
p=1
λp tanh(ωp· +θp)−
n
X
p=1
spλp tanh(spωp· +spθp) = 0, for every choice of signs sp ∈ {−1,+1}, p ∈ {1, . . . , n}, i.e., with the notation in (2.1), we have hN itanh = hN0itanh with n0 = n, λ0 =λ, λ0p=spλp, ωp0 =spλp, andθp0 =spθp, for all p∈ {1, . . . , n}.
Underlying this nonuniqueness is the simple insight that tanh(t) =
−tanh(−t) can be rewritten as tanh(t) + tanh(−t) = 0, which, in turn, can be interpreted as a single-layer network with two neurons, mapping every input to output 0.
For a more intricate example, consider the clipped rectified linear unit (CReLU) nonlinearity given byρc(t) = min{1,max{0, t}}, and note that
ρc(t)−12ρc(2t)−12ρc(2t−1) = 0, for allt∈R, (2.3) corresponds to a single-layer network with three neurons mapping every input to output 0. This can be rewritten asρc(t) = 12ρc(2t) +
1
2ρc(2t−1) and applied recursively to yield hNniρc:=
n
X
p=1
2−pρc(2p· −1) + 2−nρc(2n·) =ρc,
for all n ∈ N. In other words, we have effectively used the three- neuron network (2.3) to repeatedly replace single nodes with pairs of nodes without changing the function realized by the network, thereby constructing an infinite collection of different networks, all satisfying hNniρc =ρc.
In summary, we see that, at least for single-layer networks, non-
uniqueness in the realization of a function arises from affine symmetries of the nonlinearity, where the symmetries are none other than single- layer networks mapping every input to output 0. Namely, these ‘zero networks’ can be used as templates for modifying the structure of (more complex) networks without affecting the function they realize.
This motivates the following definition.
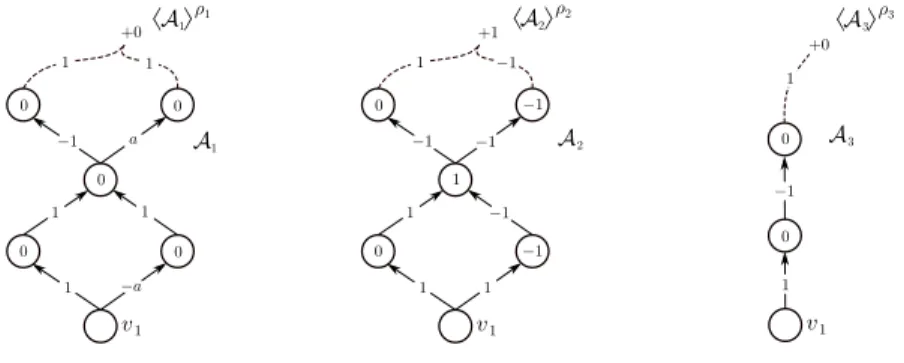
Definition 2.1 (Nonlinearity and affine symmetry). Anonlinearity is a continuous functionρ:R→Rsuch thatρ6={t7→at+b:t∈R}, for alla, b∈R. Letρ:R→Rbe a nonlinearity andI a nonempty finite index set. Anaffine symmetryofρis a collection of real numbers of the form (ζ,{(αs, βs, γs)}s∈I) such that,
(i) for allt∈R,
X
s∈I
αsρ(βst+γs) =ζ1(t), (2.4) and
(ii) there does not exist a proper subsetI0ofIsuch that{ρ(βs·+γs) : s∈ I0} ∪ {1}is a linearly dependent set of functions fromRtoR. Item (ii) in Definition 2.1 is a minimality condition, ensuring that only “atomic” symmetries qualify under the formal definition.
Note that every nonlinearityρsatisfiesρ+ (−ρ) = 0, and hence pos- sesses at least the ‘trivial affine symmetries’ (0,{(α, β, γ),(−α,β,γ)}), forα, β∈R\ {0} andγ∈R. We remark that Definition 2.1 is more general than what is needed to cover our examples above, asζ in (2.4) is allowed to be an arbitrary real number, whereas we hadζ= 0 in both of our examples. One can, of course, seek to build a theory encompassing even more general symmetries, e.g. those for which the right-hand side of (2.4) is an affine functiont7→ζ1+ζ2t (which, in the context ofρ-modification introduced later, could then be absorbed into the next layer of the network).
Our aim is to generalize the aforementioned correspondence between the non-uniqueness in the neural network realization of functions and the affine symmetries of the underlying nonlinearityρto multi-layer