Zur Geometrie der Ortskurven der graphischen Wechselstromtheorie

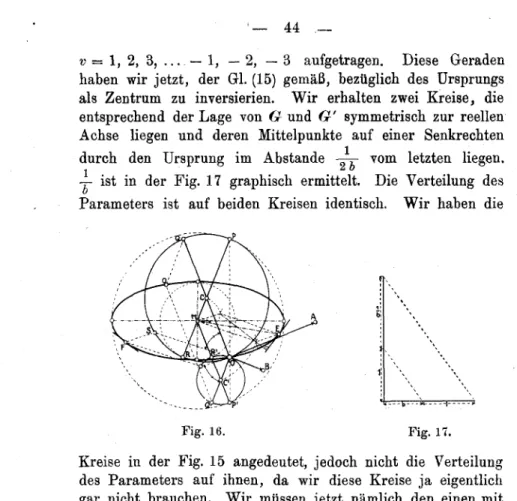
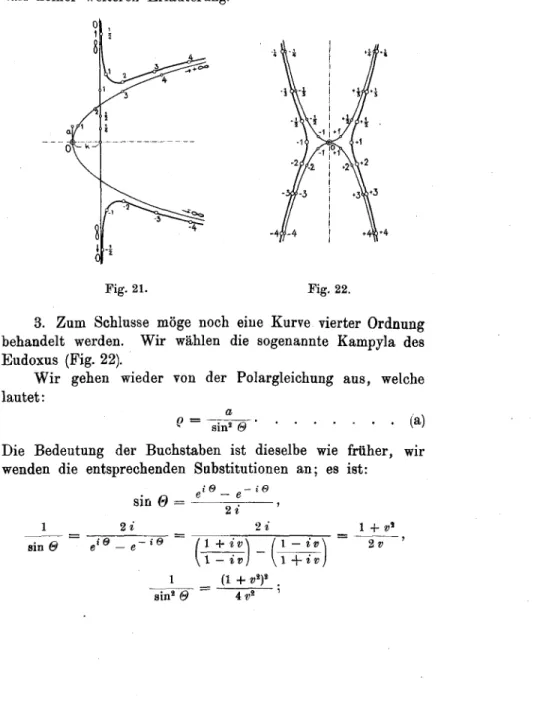
Research Collection

Doctoral Thesis

Zur Geometrie der Ortskurven der graphischen Wechselstromtheorie

Author(s):

Michael, Waldemar Publication Date:

1919

Permanent Link:

https://doi.org/10.3929/ethz-a-000095905

Rights / License:

In Copyright - Non-Commercial Use Permitted

This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use.

ETH Library

Zur Geometrie der Ortskurven der

graphischen Wechselstromtheorie

Von der

Eidgenössischen Technischen Hochschule in Zürich

zur Erlangung der

Würde eines Doktors der technischen Wissenschaften

genehmigte

Promotionsarbeit

vorgelegt ^von

Waldemar Michael

aus Wergenstein (Graubünden)

Referent: Herr Prof. ^{Dr. L. Kollros} Korreferent: Herr Prof. ^{Dr. K Kühlmann}

212.

Zürich 1919

Druck von

Metzger

^&

Wittig

ⁱⁿ

Leipzig

Leer

^-

Vide

^-

Empty

Meinen lieben Eltern

und

meiner lieben Tante

in Dankbarkeit gewidmet.

Leer

^-

Vide

^-

Empty

Vorwort

Die

vorliegende

Arbeit verdankt ihre

Entstehung

^dem Studium der Arbeiten über Wechselstromtheorie von Dr.

0. Bloch. Besonders

angeregt

^{dazu wurde ich durch den}

persönlichen

Verkehr mit dem

genannten Verfasser,

^{der mein}

Kollege

^{und Freund war.} Dr. 0. Bloch macht in seinem Buche

„Die

Ortskurven der

graphischen

Wechselstromtechnik-' darauf

aufmerksam,

^{daß in} seiner Arbeit verschiedene

Fragen speziell

mathematischer Natur noch

unerledigt

^{bleiben mußten.}

Auf S. 93 und 94 des

genannten

^{Buches heißt es:}

„Es

^kann

nicht unsere Absicht

sein,

^{in diesem}

Zusammenhange

^{tiefer in}

das Gebiet

einzudringen,

^{das sich uns hier eröffnet. Dies}

wäre zunächst

Aufgabe

^des Mathematikers von Fach. Für den

Ingenieur

^{wäre es natürlich von hohem}

^Wert,

^{wenn er}

diese Arbeit schon

geleistet vorfände,

^{so daß er in}

jedem Sonderfall,

^{auf den er in der Praxis}

stößt,

^nur

nachzuschlagen brauchte,

^{welcher Art die der Formel}

entsprechende

^Kurve

ist,

^{und wie man sie am} einfachsten aus den Konstanten der

Gleichung findet;"

und in einer Fußnote

fügt

^{er hinzu:}

„Hier

dürfte ein schönes und fruchtbares Gebiet für mathematische Dissertationen

liegen."

Ich versuchte _nun, dieser

Anregung

^zu

folgen;

^{dies um}

so

mehr,

^{als Dr.} 0. Bloch sich mit dem Gedanken

trug,

^ein Lehrbuch der

graphischen

Wechselstromtheorie zu

schreiben,

wo er vielleicht meine

Untersuchungen

^{hätte brauchenkönnen.}

Leider hat ein

tragisches

^{Schicksal diesem}

hoffnungsvollen

Plane ein

jähes

Ende bereitet.

Ich kann ^an dieser Stelle nicht

umhin,

^mit Gefühlen der Dankbarkeit des zu früh verstorbenen

Kollegen

^{und Freundes}

— 6 ^—

zu

gedenken.

^{Durch sein stets}

zuvorkommendes,

freundliches Wesen war es mir

möglich,

^{die Früchte seines kritischen}

Denkens und methodischen Arbeitens

mitzugenießen.

Meinem Freunde und

Kollegen,

^{Herrn Dr. J.}

Sauter,

dem wissenschaftlichen Mitarbeiter von Dr. 0.

Bloch,

^schulde

ich ebenfalls meinen

aufrichtigsten

Dank für seine wertvollen

Bemerkungen

^und

Ratschläge,

^{durch die meine Arbeit} ge¬

fördert wurde.

Schließlich möchte ich noch Herrn Prof. Dr. L. Kollros für seine

wichtigen Mitteilungen,

^{sowie für das}

Interesse,

^das

er meiner Arbeit

entgegengebracht hat,

meinen verbindlichsten Dank

aussprechen.

Bern,

^{im März 1919.}

Einleitung.

Die von 0.Bloch entwickelte Methode ^zur

Bestimmung

der Ortskurve eines veränderlichen Vektors bei der

graphischen Behandlung

^von

Wechselstromproblemen führt,auf

^Ausdrücke

folgender

^Art:

V^-~ ^—+

Bv±_cjl± +Jtf£

_m

D + Ev +JFV+ ... + Nvn

wo

A, S,

^{... jV}

konstante, beliebig gerichtete, gegebene

^Vek¬

toren in der

Ebene,

d. h. konstante

komplexe

oder reelle Zahlen

sind,

^{während v} ein Parameter

bedeutet,

der alle reellen Werte

von +00 bis ^—oo annehmen kann. Ein solcher Ausdruck stellt eine vektorielle

Gleichung

^{für den Ort des Vektors V}

dar;

^{wirkönnen sie kurz als die}

Ortsgleichung

^{des Vektors V}

bezeichnen. Um einen Einblick in die

Bedeutung

^dieser

Gleichung gewinnen

^zu

können,

^{sei mir}

gestattet,

^mit

wenigen

Worten auf die

Grundlagen einzutreten,

^{auf die} die Theorie

von 0. Bloch beruht.

0. Bloch hat zum ersten Male in klarer Weise

gezeigt,

daß zur

eindeutigen Beschreibung

^{des in einer Wechsel¬}

strommaschine sich

abspielenden physikalischen Vorganges

^die Kenntnis des

Wicklungssinnes

^{und die}

Aufstellung

^eines

Raumdiagrammes

^{neben dem}

Zeitdiagramm

^im

allgemeinen

unerläßlich sind. Unter dem

Begriffe „Raumdiagramm"

^ver¬

steht man ein Schalt- und

Wicklungsschema

^mit

Angabe

^des

Wicklungssinnes,

welches Schema

zugleich

ein räumliches Be¬

zugssystem darstellt,

bei welchem durch

,,Zählpfeile"

^{die Rich¬}

tungen angegeben sind,

^nach welchen die veränderlichen

physi¬

kalischen

Größen,

^{d. h. hier} die elektrischen und

magnetischen

Zeitvektoren, positiv

^zu nehmen sind. Die

Einführung

^des

Raumdiagrammbegriffs

bedeutet für die Wechselstromtheorie

— 8 ^—

einen wesentlichen Fortschritt. Es ist hier nicht der

Ort,

diese

Behauptung eingehend

^zu

begründen;

^wir verweisen dies¬

bezüglich

^{auf die}

Originalarbeit

^von

O.Bloch.1)

Die

folgende

^kurze

Darlegung möge genügen,

^{um eine}

Vorstellung

^{von der}

Rolle,

^{welche das}

Baumdiagramm spielt,

zu

geben.

Ist einmal das

Raumdiagramm

^{für ein zu} untersuchendes

Objekt festgelegt,

^{so hat es keine}

Schwierigkeit mehr,

^den darin sich

abspielenden physikalischen Vorgang

ⁱⁿ

eindeutiger

Weise mathematisch zu erfassen. Zu dem Ende hat man nur

noch die

(erweiterten)

Kirchhoffschen Gesetze so oft an¬

zuwenden,

^als

Knotenpunkte

^und

geschlossene

Stromkreise vor¬

handen

sind,

^{und diese}

Operation

kann nunmehr sozusagen mechanisch

ausgeführt

^werden. Man erhält auf diese Weise eine Anzahl linearer

Gleichungen

^zwischen den elektrischen und

magnetischen

Vektoren und zwar ebensoviel voneinander

unabhängige Gleichungen,

^als die Zahl der Unbekannten des Problems

beträgt.

^{Aus diesem}

Gleichungssystem

^{kann nun}

irgendeine

^dieser Unbekannten bestimmt

werden,

als Funktion der

gegebenen

^{Größen des Problems. Verändern wir nun eine}

dieser

gegebenen ^Größen,

^{indem wir einen sie messenden}

reellen Parameter

beliebige

^Werte durchlaufen lassen und setzen wir die

übrigen

^{Größen als konstant} voraus, ^{so er¬}

scheint die zu bestimmende Größe als Funktion des Para¬

meters. Stellt nun die

gegebene

veränderliche Größe eine rationale Funktion des Parameters

dar,

^{was immer voraus¬}

gesetzt

^werden

kann,

^{so wird auch die zu} bestimmende Größe eine rationale ^— im

allgemeinen gebrochene

^{— Funktion}

dieses Parameters sein. Bezeichnen wir die zu bestimmende Größe mit

V,

den Parameter mit v und die

gegebenen

^Kon¬

stanten mit

A,

^{B ...}

N,

^so erhalten wir für V einen Aus¬

druck von der Form der Gl.

(1).

^{Da V} bei kontinuierlicher

Änderung

^{von v eine}

gewisse Kurve,

^{die man die Ortshurvc}

von V

nennt, durchläuft,

^{haben wir die Gl.}

(1)

^die

Ortsgleichvng

von V

genannt.

^Die

Aufgabe,

welche sich nach

Aufstellung

dieser

Gleichung darbietet,

^lautet:

x) ^{Dr. 0.}Bloch, „Die Oi'tskurven der graphischen Wechselstrom- technik nacheinheitlicherMethodebehandelt.1' Verlag^vonRascher&Cie.,

Zürich 1917.

Man soll aus der

Ortsgleichung

des Vektors V die Ortskurve desselben bestimmen.

Dabei handelt es sich einmal

darum,

^zu

wissen,

^{was für} einen

geometrischen

^{Ort diese}

Gleichung jeweils

darstellt und zweitens wird

verlangt,

^{daß die Kurve mitHilfe der}

gegebenen

Konstanten auf

möglichst

einfache Weise

gezeichnet

^werde.

Die nähere

Bestimmung „auf möglichst

einfache Weise" ist darum ausdrücklich

beigefügt,

^{weil die}

Aufzeichnung

^derKurve

stets in derWeise

erfolgen kann,

^{daß man} in Gl.

(1)

^{der Eeihe}

nach bestimmte Werte von v

einsetzt, jedesmal

^{den Vektor V} berechnet und mit Hilfe eines

Koordinatensystems graphisch aufträgt,

^womit

jeweils

^ein

Kurvenpunkt

^bestimmt

ist;

^allein diese rein rechnerische Methode ist erstens oft sehr zeit¬

raubend und zweitens

ungenügend,

^{weil sie doch in den}

meisten Fällen über den Charakter und den Gesamtverlauf der Kurve keinen

befriedigenden

^Aufschluß

gewährt.

^{Um zu} dem

gewünschten

^{Ziele zu}

gelangen,

^{wird man daher anders}

verfahren müssen. Man wird aus der

Ortsgleichung

^die geo¬

metrischen

Eigenschaften

^derKurve ableiten müssen und die¬

jenigen

Elemente der Kurve

bestimmen,

^{die für}die Konstruk¬

tion derselben von wesentlicher

Bedeutung

^sind:

Tangenten, Asymptoten, Mittelpunkte, Achsen, Doppelpunkte

usw.; ^m.a.

W.,

man wird eine

geometrische

^{Diskussion der}

Ortsgleichung

^vor¬

zunehmen haben.

Vorliegende

Arbeit befaßt sich nun mit dieserrein mathe¬

matischen

Aufgabe.

^{Um die}

physikalische Bedeutung

^der

Gl.

(1)

kümmert sie sich im weiteren nicht. Sie ist also aus¬

schließlich dem mathematischen Ausbau der Bloch'sehen Theorie

gewidmet.

Zur

Behandlung

^{der eben}

geschilderten Aufgabe

^können

verschiedene

Wege eingeschlagen

^{werden. Man kann bei¬}

spielsweise

^{mit 0. Bloch so}

^vorgehen

^— und das ist auch das

Nächstliegende

—, daß man die Gl.

(1)

^{mit Hilfe der}

Methoden der

allgemeinen analytischen

^{Geometrie und der}

aus letzterer bekannter Sätze untersucht. Man kann aber auch

gewissermaßen umgekehrt vorgehen

^— und das soll im

folgenden

^{versucht werden — und aus der Gl.}

(1)

in direkter

Weise,

^d. h. ohne die vektorielle Ausdrucks- und

Vorstellungs¬

weise zu

verlassen,

^die

Eigenschaften

^der Kurve ableiten und

— 10 ^—

aus diesen

Eigenschaften

^{auf den}

allgemeinen geometrischen

Charakter der Kurve schließen. Indem man diese Methode

konsequent durchführt, gelangt

^{man zu einer}

eigentlichen Vektoreûgeometrie.

Es hat sich

herausgestellt,

^{daß man auf}

diesem

Wege

^{nicht nur bekannte Sätze auf sehr einfache} Weise beweisen

kann,

^{sondern daß} man neue, für die Zwecke der Theorie

wichtige

^{Sätze und} Konstruktionen findet. Dieser Umstand

rechtfertigt

^die

Einführung

^{der neuen Methode neben}

der früher

angewandten,

^{die dadurch nichts von ihrem Werte}

verliert,

^zur

Genüge.

Wir bemerken noch

folgendes bezüglich

^der

Bezeichnung

der in den

folgenden Untersuchungen

vorkommenden Größen:

Vektoren

(komplexe Größen)

^{werden mit}

fettgedruckten

Buchstaben des

großen

lateinischen

Alphabets

bezeichnet. Das

gleiche

Zeichen zwischen zwei senkrechten Strichen bedeutet wie üblich den absoluten

Betrag

des Vektors.

Skalare

(reelle Größen)

^{werden mit} kleinen lateinischen Buchstaben bezeichnet.

Die

imaginäre

^{Einheit bezeichnen wir mit i.}

§1-

Die Rationalität der Ortskurven.

Satz: Durch die

Gleichung (1)

^{wird eine rationale}

algebra¬

ische Kurve

dargestellt.

Der Beweis dieses Satzes

gestaltet

^{sich sehr einfach.}

Denken wir ^uns nämlich die Vektoren

A,

^{B, ... W als kom¬}

plexe

^Zahlen

geschrieben,

^{etwa so}

A = a1 + ⁱai H ⁼

/j1

^{-j- i}

b%

^{... JV =} nY +

in,,

so läßt sich Gl.

(1)

^schreiben:

TT_ (ai ^{+ *}

a*)

^{+ (*•}

+_*'

^**)v

"t

^{(c> +}

ica}v* +_

•_ +(mt +ⁱwa)^v"1

"

"(d,

+

idj>

+ (<?,+

~ie,~)v

+{f1+ifi)vi^+... + (w, +iw.2)vn

__

(a, +b,^{v +} c, î)2^+... + TW,«O+i(a,+b2^v+ e2v*+...4- m^»'") (d, ⁺e2^{v +}/",^{vl +...}+ nxvn) +i(d2+e2v⁺/j^v'+

...~+n^v")

^'

in den Klammern stehen ganze rationaleFunktionen mtenund

«ten Grades von v. Wir können daher in leichtverständlicher

Abkürzung

^schreiben:

I

Machen wir den Nenner

reell,

^so

folgt:

F= ffi"' Vi"" ⁺W"' W'^{+ i}W°v.'"'^-<pi"°' W") _n un

Dieser Bruch läßt sich in einen reellen und einen rein

imagi¬

nären Teil

zerlegen

^{und etwa} in der Form schreiben:

F=

Q>[v)

+

iW(v), (lc)

wo 0 und W rationale

gebrochene

^{Funktionen von}

(«)

^sind.

In dieser

Gleichung

^{erscheint V in} zwei zueinander senk¬

recht stehenden

Komponenten zerlegt.

Diese können wir als die

rechtwinkligen

kartesischen Koordinaten der Kurve deuten.

Bezeichnen wir dieselben mit x und _y, so erhalten wir:

V=x

fi>

^{und X==}

*fjü!

^{. , . .}

^(Id)

Damit ist unser Satz

bewiesen,

denn rationale Kurven sind eben

solche,

deren Koordinaten sich als rationale Funk¬

tionen eines Parameters darstellen lassen.

Bestimmuny

^der

Ordnung

^{der Kurve.}

Diese

Aufgabe

^ist

eigentlich

^im

vorigen Paragraphen

^schon

gelöst,

^{denn aus dem Grade der Funktionen 0 und W läßt}

sich bekanntlich die

Ordnung

^der betreffenden Kurve

angeben.

Wir wollen

jedoch versuchen,

auf vektoriellem

Wege

^zum

Ziele zu

gelangen.

^Zu dem Ende denken wir uns die durch Gl.

(1) dargestellte

^{Kurve mit einer}

beliebigen

^{Geraden zum} Schnitte

gebracht.

^{Die Zahl der}

Schnittpunkte (im algebra¬

ischen

Sinne)

^{definiert uns die}

Ordnung

^{der Kurve. Bevor}

wir aber dies wirklich ausführen

können,

^{müssen wirzunächst} darüber im Klaren

sein,

^wie eine Gerade vektoriell

dargestellt

werden kann. Es ist nun unschwer zu

erkennen,

^{daß wireine} Gerade stets durch eine lineareFunktion des Parameters dar¬

stellen

können,

^{z. B.}

folgender

^Art:

O^JP+Qv (2)

Daß die Gl.

(2)

tatsächlich eine Gerade in

allgemeiner

Lage darstellt,

^{ist an} fland der

Fig.

¹ sofort einzusehen.

— 12

P ist ein konstanter

Vektor,

^{zu dem}

jeweils

^{ein zum kon¬}

stanten VektorP

paralleler

^Vektor

Q

^{v zu} addieren ist. Da v von +oo bis ^—oo variieren

kann,

^ist

klar,

^{daß wir als Ort}

Fig. ^1.

des Vektors G die durch den

Endpunkt

^{von 1*zu}

Q parallele

Gerade bekommen.

Mit einer solchen Geraden wollen wir die Kurve

(1)

^zum Schnitte

bringen.

Zu dem Zwecke verfahren wir

folgender¬

maßen:

Wir denken uns die Kurve und die Gerade um den Vektor

— P verschoben. Die Gerade G

geht

dann durch den Ur¬

sprung und ihre

Gleichung geht

^{über in:}

<?'= G-P=

Q-vssfa +igt)v.

Die

Gleichung

^{der Kurve}

geht

^{über in:}

wobei wir

gesetzt

^haben:

-P ⁼Pi +

2>2 0

⁼ _9i

+i(h

und indem wir

jetzt

^{für Vden} Wert der Gl.

(lb)

^benutzen:

v, +i

[W*">

^{Vi'"'- <''}

V.°"_-

^Pi

((V.")'

⁺

(V»")')]

~~

1W"]2⁺

ÎW"']4

V deckt sich nun für

gewisse

^{Werte von v mit G und}

zwar offenbar so

oft,

als G die Kurve schneidet. Zur Be¬

stimmung

^dieser

Schnittpunkte

^{bzw. der}

zugehörigen

^Para¬

meterwerte

„»"

^auf „F" benutzen wir die

Bedingung,

^daß

der Vektor V die

gleiche Richtung

wie der Vektor G' haben soll. Als Ausdruck für die

Richtung

^{können wir die}

^trigono¬

metrische

Tangente

^{des Winkels}

nehmen,

^{den die Vektoren}

mit der

positiven Richtung

der reellen Achse bilden. Diese

Tangente

^ist

gleich

^dem

Quotienten

^{aus der}

imaginären

^Kom¬

ponente

^{durch die reelle}

Komponente.

^{Indem wir diesen}

Quotienten

einerseits für V und andererseits für G' bilden und die erhaltenen Werte einander

gleichsetzen,

erhalten wir die

Gleichung:

(<P,%){m+"»

^-

(^y8r+">

^-jPsKv,"")2⁺(y/y\

= q, ^,„.

(<fiWi)<m+"}⁺(<*>*%)(+*"^-^{(v,w)2⁺(W'ï'l <?i u Das ist nun eine reelle

Gleichung

^{für die}

Berechnung

von v. Wir erhalten offenbar ebensoviel

Schnittpunkte (im algebraischen Sinne),

^{als die Gl.}

(3)

^Wurzeln

hat;

^{m. a. W.:}

Dem Grade der Gl.

(3) entspricht

^die

Ordnung

^{der Kurve}

(1).

Die

Ordnung

^{der Kurve}

(1)

^{ist durch die Gl.}

(3) eindeutig

^und

zwar genau in

Übereinstimmung

^mit den Resultaten der all¬

gemeinen analytischen

Geometrie bestimmt. Wir

bemerken,

daß diese

Bestimmung unabhängig

^{ist von} der Art der Para¬

meterverteilung

^auf der Geraden

G;

^{denn bei der}

Bildung

^der

Gl.

(3)

^{fällt der Parametervon G}

^überhaupt

heraus. Wir haben in Gl.

(2) speziell

^{eine lineare}

Verteilung

^des

Parameters,

d. h. eine

solche,

bei welcher

jedem

^{Punkte der Geraden nur}

ein Parameterwert

entspricht

^und

umgekehrt,

angenommen.

Wir hätten aber

ebensogut

^{eine andere}

Verteilung

^{des Para¬}

meters annehmen

können,

^{indem wir an Stelle von v}

irgend¬

eine reelle Funktion von v gesetzt

hätten;

^am

Resultate,

^{d. h.}

am Grade der Gl.

(3)

^{hätte das nichts}

geändert;

^{denn in}

letzterer kommen von der Geraden G immer wieder nur die Konstanten plt pi} qx, q2 ^vor.

Dagegen

^{ist der Grad der}

Gl.

(3)

^nicht

unabhängig

^von der Art der

Parameterverteilung

auf der Kurve

(1).

^{Wir können die Ortskurve als eine konti¬}

nuierliche

Punktfolgö auffassen,

bei welcher

jeder

^{Punkt so}

oft zu zählen ist, ^{als ihm Parameterwerte}

zukommen;

^den

Linienzug,

^auf welchem die Punkte ^zu

liegen kommen,

^können

wir als den

„Träger"

^der

Punktfolge

bezeichnen. Es ist zu

beachten,

^{daß die}

Ordnung

^des

^Trägers

^{von der}

Ordnung

^der

Ortskurve,

^{zu der er}

gehört,

verschieden sein kann und ^zwar

niedriger,

indem einem Punkte des

Trägers

mehrere Para¬

meterwerte, also mehrere Punkte der

Ortskurve, entsprechen

können. Nur im Falle einer

„linearen" Verteilung

^{des Para-}

— 14 ^—

meters sind Ortskurve und

Träger

^{auch der}

Ordnung

^nach identisch. Aus dieser

Auffassung folgt

^ein wesentlicherUnter¬

schied zwischen einer Kurve im

gewöhnlichen

Sinne und einer Ortskurve. Erstere stellt einfach einen

(oder mehrere)

^Linien¬

züge dar,

^{letztere stellt} eine auf einem

Linienzug

^{in bestimmter}

Weise verteilte

Punktfolge

^{dar. Daraus}

folgt,

^{daß bei der}

zeichnerischen

Darstellung

einer Ortskurve die Parameterver¬

teilung

^{auf ihr stets mit}

anzugeben

^{ist. Ohne diese}

Angabe

entbehrt die

Figur

^eines

eindeutigen Sinnes; dementsprechend

ist sie auch

praktisch

^{ohne Wert. Weiter}

folgt daraus,

daß eine Ortskurve nicht allein nach der Gestalt ihres

Trägers

^{benannt werden}

darf,

^{wenn diese}

Benennung

^einen

eindeutigen

Sinn haben soll. Es wird

zweckmäßig sein,

^nur

dann die Ortskurve einfach nach der Gestalt des

Trägers

^zu

benennen,

^wenn derParameter linear auf ihr verteilt

ist,

^d.h.

wenn

Träger

und Ortskurve von

gleicher Ordnung

^{sind. Ist}

das nicht der

Fall,

^{so wird man zu} dem Namen des

Trägers

die

Ordnung

der Ortskurve mit anführen. Nach dieser Ver¬

abredung

^bedeuten:

Gerade, Kreis, Kegelschnitt

^{usw. Orts¬}

kurven erster bzw. zweiter

Ordnung.

^{Haben wir z. B. auf}

diesen Kurven eine

quadratische Parameterverteilung,

^{so reden}

wir von einer Geraden zweiter

Ordnung,

einen Kreis vierter

Ordnung

^{usw. Offenbar ist die}

Ordnung

einer Ortskurve ent¬

weder

gleich

^oder ein ganzes Vielfaches der

Ordnung

^ihres

Trägers.

Aus der Gl.

(3)

^{läßt sich eine einfache}

Regel

^{zur Bestim¬}

mung der

Ordnung

^{der Kurve}

(1)

^ableiten:

Denken wir uns in Gl.

(3)

^{die Brüche}

weggeschafft,

^alle

Glieder auf die linke Seite

gebracht

^und nach Potenzen von v

geordnet,

^{so erkennt man}

leicht,

^daß ihr Grad entweder

{m

⁺

n)

oder

(2n) ist, je

^{nachdem m} > ⁿ oder m < ⁿ ist. Oder wir haben die

Regel:

^Die

größere

^derZahlen

(m

⁺

n)

^und

(2n) gibt

die

Ordnung

^{der Kurve}

[1)

^an.

Bei der

Ableitung

dieses Resultates haben wir angenommen, daß der Nenner in Gl.

(1)

^ein

komplexer

^Ausdruck

sei,

^den

wir zuerst reell machen mußten. Im

Sonderfalle,

^{wo der}

Nenner von vornherein in reeller Form

erscheint,

oder wo

sämtliche Koeffizienten im Nenner

gleichgerichtete

^Vek¬

toren

repräsentieren,

^so daß nach einer

passenden Drehung

der

Figur

dieselben mit der

Richtung

der reellen Achse zu¬

sammenfallen und der Nenner wieder reell

ist, brauchen

^wir

die Gl.

(1)

^{nicht erst} abzuleiten. Man

überzeugt

^sich

leicht,

daß dann an Stelle der Gl.

(3) folgende Gleichung

^tritt:

wo mit

1//"*

^der reelle Nenner in der

Vektorgleichung

^be¬

zeichnet wird. Die Gl.

(3')

^{ist vom Grade m oder n}

je

^nach¬

dem m >ⁿ oder m < ⁿ ist. Wir haben daher die

Regel:

Erscheint der Nenner einer

Ortsgleichung

^{in reeller}

Form,

so

gibt

^die

größere

^{der Zahlen m und n die}

Ordnung

^der

Kurve an.

Fehlt in Gl.

(1)

^{der Nenner}

überhaupt,

^d. h. ist die reelle Seite von

(1)

^eine ganze Funktion waten Grades von

V,

^{so er¬}

kennt _man, daß die

entsprechende

^{Kurve mter}

Ordnung

^ist.

Wir wollen ^nun definieren:

Eine

FeJt'orgleichurig,

^{die eine Ortskurve mter}

Ordnung

^dar¬

stellt, soll eine Form inten Grades

heißen.

Da wir

jede

^{Form mten Grades mit}

komplexem

^Nenner

auf eine Form desselben Grades mit reellem Nenner

bringen können,

^{nicht aber}

umgekehrt,

^so

folgt,

^{zusammen mit}

dem,

was wir über die

Ordnung

^{einer Kurve}

abgeleitet

^{haben: Die}

allgemeinste ^Form,

^{auf die die}

Gleichung

^{einer Ortskurve mter}

Ordnung gebracht

^werden

kann,

^{oder kurz die}

allgemeinste

Form mten Grades kann

geschrieben

^werden:

=

A +Bt + Cvi + ...+M vm _f4.

a + b v +cv*-\-^{. ..} -\-^nvn

' ' '

^

wobei ms=re angenommen ist.

Diese Annahme bedeutet keine

Einschränkung,

^{denn wir}

können stets

bewirken,

^daß m^n ^{sei. Um dies}

einzusehen,

müssen wir nun

beachten,

^{daß der Fall m < n}

besagt,

^daß

die Kurve durch den

Ursprung geht,

^{indem nämlich V= 0}

für v = oo wird.

Bringen

^{wir die Kurve in eine}

allgemeine Lage,

^{was dadurch}

geschieht,

^{daß man zu V einen}

beliebigen

konstanten Vektor T

addiert,

^wodurch natürlich derCharakter der Kurve in keiner Weise beeinflußt

wird,

^{so sieht} man, indem man rechts alles auf

gleichen

^Nenner

bringt,

^{daß der}

Zähler mindestens vom Grade des Nenners

wird,

^{w. z. b.w.}

— 16 ^—

Aus

(4)

^{erhalten wir eine}

spezielle

^{Form mterx}

Grades,

wenn wir

verlangen,

daß der Nenner ein

komplexer

^Aus¬

druck sei.

Diese Form wird

allgemein folgendermaßen geschrieben

werden können:

y= ^{A +}

By

^{+ Ce«+ .. .}

+L»J^

^{, ,}

wo p^sS— anzunehmen

ist,

^{wenn m —}

p^p

^{sein soll.}

Wir werden uns im

folgenden

^{mit dieser}

speziellen,

^bei

Wechselstromproblemen

^sehr

häufig

auftretenden Form

(4') eingehend beschäftigen

^{und werden}

sehen,

^{daß sie}

speziell

eine zirkuläre Kurve darstellt, während

(4)

^{auch die nicht}

zirkulären Kurven umfaßt.

§3-

Die

Tangente

^{in einem Punkte der Kurve.}

Zur

Bestimmung

^der

Eichtung

^der

Tangente

^{in einem}

Punkte der Kurve dient der

folgende

^leichtzu beweisende Satz:

Der

Differentialquotient

^des Kurvenvektors nach dem Para¬

meter ist ein der

Tangente

^im

Endpunkte

dieses Vektors par¬

alleler Vektor.

Betrachten wir nämlich zwei Vektoren

(Fig. 2) Vx

^und

F2

einer

gewissen Kurve,

^{so ist die} Differenz JV=

V2

^—

V^)

nichts anderes als die

Sehne,

welche die End¬

punkte

beider Vektoren verbindet. Eückt

Vt

unendlich nahe an

Vx ^heran,

^so

^geht

^{die Sehne}

indasKurvenelement über. Aus der DifferenzAV wird das Differential dV. Bildet man daher den

Differentialquotienten

——, so erhält man

offenbar einen

Vektor,

^{der dieselbe}

Richtung

^{hat wie}

dV,

d. h. wie die

Tangente

^{in diesem}

Punkte;

^denn die Division durch die reelle Größe

(dv)

hat keinen Einfluß auf die

Eichtung

des Vektors dV.

l) Bemerkung: ^{Bei dieser} Gelegenheit ^{wollen wir ein}

für allemal verabreden, ^{daß die}Verbindungslinie ^{der End¬}

punktezweier durchdenselbenUrsprung gehenden Vektoren,

die zweiteDiagonale^desVektorenparallelogramms^heißen soll, ^sie stellt also derenDifferenz dar. Die Summe beider Vektoren bezeichnen wir als erste Diagonale (Fig.3).

Y

AV

Fig.^3.

§4.

Die

Bestimmung

^der

Asymptoten.

Für die

Bestimmung

^der Gestalt einer Kurve ist bekannt¬

lich die

Ermittlung

^der

Asymptoten

^von

größter Wichtigkeit.

Wir werden uns daher

fragen:

Wie lassen sichdie

Asymptoten

einer

Kurve,

die durch eine vektorielle

Gleichung gegeben ist,

bestimmen? Diese

Aufgabe

^{können wir in} ganz

allgemeiner

Weise

lösen,

^{auf Grund des im}

folgenden

entwickelten Ver¬

fahrens.

Wir haben

gesehen,

^{daß die}

Gleichung

einer Kurve mter

Ordnung

^{immer auf die Form}

gebracht

^{werden kann:}

V=

A + Bv + Cv* +" ' " +

—— (4)

wobei rn^in ^{ist. Der Fall m} < ⁿ

(Kurve

^{durch den}

Ursprung)

erheischt keinerlei besondere

Betrachtungen.

Den Ausdruck rechter Hand in

obiger Gleichung

^können

wir durch Ausdividieren in eine _ganze Funktion

(bzw.

ⁱⁿ

eine

Konstante)

^{und in eine echt}

gebrochene

^Funktion

zerlegen.

^{Diesen echten Bruch können wir dann weiter in} Partialbrüche

zerlegen.

^{Zu dem Zwecke hat man die}

Wurzeln des Nenners ^zu bestimmen. Mit

Bezug

^{auf letztere} sind zu unterscheiden:

einfach und mehrfach auftretende.

Die Gl.

(4)

^{kann demnach}

folgendermaßen geschrieben

^werden:

0 1 1 1 ^{^ "}

wo

JP, Q, -R,

^konstante Koeffizienten

(Vektoren)

^{bedeuten und}

v , v Wurzelwerte sind.

a x

Aus der Gl.

(5)

ersehen wir sofort

folgendes

^{: Der Vektor}

V wird _oo, d. h. die Kurve hat einen reellen Punkt im Un¬

endlichen für:

1. v = ± ^oo falls der erste

Polynom

Michael,^{Diss. 2}

— 18 ^—

sich nicht auf eine Konstante reduziert

[rn

^{= n) oder} ganz fehlt. Das ist dann der

Fall,

^{wenn m} < ⁿ ist. Somit sehen wir aus

(5),

daß dieser Fall darin als

Spezialfall

^enthalten

ist,

2. für v = einem Wurzelwerte. Dabei interessieren uns nur die reellen

Wurzelwerte;

^{denn nur diesen}

entsprechen

reelle Punkte der Kurve und nur für diese kommen reelle

Asymptote

^{in Betracht.}

Die

Richtung

^{des unendlich}

groß

^werdenden

Vektors,

das heißt die

Richtung

^{nach dem unendlich}fernen Punkte der Kurve ist ebenfalls sofort zu bestimmen:

1. Denken wir uns v ⁼ od in

(5) eingesetzt,

^{so werden}

sämtliche Brüche rechts zu

Null;

^{aus dem}

übrigbleibenden Polynom

klammern wir ^ve aus; ^man erhält dann etwa

-P„ 1 p p

setzen wir dann v ⁼ oo

ein,

^so verschwinden in der Klammer sämtliche Glieder bis auf P . Der Vektor _P_, d. h. der Koeffi- zient der höchsten Potenz von v, bestimmt dann die

Richtung

des unendlich fernen Punktes mit dem Parameterwert «=oo.

2. Für einen reellen

Wurzelwert,

^z._{B. va} ^bzw. _vx, ^verfahren

wir

analog:

^{wir klammern}

alleinal

den Bruch

bzw. \d

Va (v^- VTf

aus sämtlichen

Summengliedern,

^{in der} Klammer bekommen wir dann sämtliche Glieder den Faktor

(v

^—

va)

^bzw. (v ^—») mindestens in der ersten

Potenz,

mit Ausnahme der Vektoren

Q

bzw. B ,. Bei Einsetzen der Wurzelwerte v bzw. v ver-

schwinden somit sämtliche Glieder in der Klammer bis auf

Qa

^bzw.

Ut

d. Diese Vektoren bestimmen somit die

Richtung

nach dem betreffenden unendlich fernen Punkte der Kurve.

Wir

fragen

nun, wie bestimmt man die

Asymptoten?

^Die

Lösung

^dieser

Frage

^{ist im}

folgenden

Satze enthalten.

Die

geradlinigen Asymptoten

werden durch die reellen ein¬

fachen

Wurzeln des Nenners und den Parameterwert v ^«=4;00,

falls

^{das erste}

Polgnom

eine lineare Funktion in v ist, bestimmt.

Sie werden dadurch

konstruiert, daß

^man einen dieser Werte in sämtliche Glieder der rechten Seite der Gl.

(5)

^mit Ausnahme des dabei unendlich

groß

^werdenden

Gliedes, einsetzt,

und durch den

Endpunkt

^{des so erhaltenen}

(endlichen) Vektors,

^{die Parallele}

zur

Richtung

nach dem unendlich

fernen

^{Punkte zieht.}

Wir haben zu

beweisen,

daß die nach der

gegebenen

^Vor¬

schrift konstruierte Gerade die Kurve in dem betreffend un¬

endlich fernen Punkt

berührt,

^{d. h. zwei}

(unendlich benachbarte)

Punkte mit ihr

gemeinsam hat, oder,

^{daß sie} die

Kurve,

^außer

im

Berührungspunkt

^{nur noch im}

(m

^— 2) Punkte

schneidet,

wenn m die

Ordnung

der Kurve bedeutet.

Beweis:

1. Es sei _{vk eine} reelle einfache Wurzel. Wir bilden vor¬

schriftsmäßig

^aus

(5)

den Vektor:

0 1 11

Wir haben nun im

Endpunkte

dieses Vektors eine Gerade

parallel

^{zum Vektor}

Qk

^zu

^ziehen,

^{d. h. also die Gerade}

G ⁼

Vk

⁺

Qk

^{v zu} konstruieren und die Zahl der Schnitt¬

punkte

^{derselben mit der Kurve zu bestimmen.} Eine solche

Aufgabe

^{haben wir} bereits bei der

Bestimmung

^der

Ordnung

einer Kurve

gelöst.

^{Wir verfahren hier in}

analoger Weise;

demnach haben wir die Gerade und die Kurve um den Vektor

(— Vk)

^zu verschieben. Wir erhalten für die Kurve die neue

Gleichung:

' s

\

Daraus haben wir eine

analoge Gleichung

^zu

(3)

^zubilden.

Die Gerade G' ⁼ G^—

Vk

⁼

Qk

^v liefert für die

trig. Tangente

ihres

Richtungswinkels

^{den Wert:}

-^-;

^wenn

_Qk

⁼

(Çik+^fj2t) gesetzt

^{wird. Setzen wir auch in}

(5"')

2*

— 20 ^—

denken wir uns reelle und

imaginäre Komponente

^von ge¬

trennt und durcheinander

dividiert,

^so erhalten wir die zu

(3) analoge Gleichung:

0 1

t d

l l ^{T v *}

_q%k.

j~ ₊

yipi0de

^- _*£)+

yi**qla ^(——

^-1

⁾

v^-Vi jiLd ^s — \ ^v- T„ ^{fi -}va^!

0 1

t d

Die linke Seite dieser

Gleichung

^{dürfen wir mit} (v ^—

vk)

^er¬

weitern,

^{und erhalten nach}

Wegschaffung

^{der Nenner links}

und rechts in leicht verständlicher

Abkürzung:

?i*-ft*⁺

'A>- »012(2)

⁺

2<2)

⁺

22(2)1

= yi*-92* +

?»(*

^-

»»EW

⁺

2(^

⁺

22(^1;

die Glieder glk-g2l heben sich

gegenseitig

^{auf. Die}

Gleichung

ist dann teilbar durch

(»

^—

c^,

wodurch sich ihr Grad um 1 vermindert. Das

bedeutet,

^{daß unsere Grade die Kurve im}

Punkte v ⁼ vk einmal schneidet, ^was wir zwar bereits

wissen;

denn sie ist

ja

^zu

Q parallel.

^{Soll die Gerade die Kurve im}

Punkte v^—rk

berühren,

^{so muß die Gl.}

(6)

^{den Faktor}(v^—

v,)2 enthalten;

^{das ist aber auch der}

Fall;

^{wir können nämlich}

zeigen,

^daß

jedes Summenglied

^den Faktor (v ^—

vk)

^{auch enthält.}

r

Zunächst ist diesoffensichtlichfür dieGlieder:

"^sp

(ve^— »s);

u ^e

denn

(ve

^—

vke)

^{ist stets durch} (v^—

vk) ^teilbar,

^{ferner ist:}

}

_

J;

^{(p*- O - (» - ra)} __

y ^- rk v-v„ ^vk-v„ (v- va) (vk^- v„) (» ^- va)(rt ^- v„) ^* im Zähler eines

jeden

Summanden steht der Faktor

(/•

^—

vk);

und endlich ist

1

1__

= (Vk-

v,?-

^(v-

vj

(v ^-

vrf

(tt^-

v/

[(» ^-vt)(vh^-

vt)]a

'

'

nun ist

to>-r1?

⁼

i>ti-avlli-i*z+(-))vk'-\*+ +(-l)'-,3.r,rta-1+(-l)V

=

-[(«'-t>*a;

⁺

3(»a-1-t>i'-1)«t+...+(-l)'-1.«(«-»fc)rt4-1]

aus diesem

Polynom

^{kann man wieder}

(»

^—

Ȁ) ausscheiden;

daraus ist also

ersichtlich,

^{daß man den Faktor}

(v

^—

v^j

^überall

ausklammern

kann;

^{somit kommt vor die} Klammer tatsächlich der Faktor

(v

^—

vh)2.

^{Die Gl.}

(6)

^{ist nach}

Kürzung

durch diesen Faktor um 2 in der

Ordnung erniedrigt,

^{w. z. b. w.}

2. Wir haben ferner zu

zeigen,

^{daß man für » ebenfalls}

r

eine

Asymptote erhält,

^{falls das}

Polynom 2e

^{-P„ve linear}

^ist,

o ^s

also etwa Av + ^B

geschrieben

werden kann.

Der Beweis ist leicht zu

führen,

^{wenn wir die} Sub¬

stitution einführen:

l

" ^— i !

was stets erlaubt

ist,

^weil

ja

^v alle reellen WTerte von +oc bis —oo annehmen kann (»0 ⁼

Konstante).

^{Dem Werte «=oc}

entspricht

^{der Wert v =} »0. Die Gl.

(5) geht

^{über in:}

1

+

y,yiBrô^L^L

Bilden wir den dem Vektor

Vk entsprechende

^Vektor

V0'

durch Einsetzen ^{von »' =} _v0, so erhalten wir einfach V ⁼ B.

Durch den

Endpunkt

^{von B ist}

jetzt

^{die Parallele zum}

Vektor A zu ziehen. Wir bilden nun die

(6) entsprechende

Gleichung

^{und erhalten: *}

22

v'-v„ *'jLj l-v„(v'-vtt)

-v0) >* rtt(t/-v0)

-J

^1 ^{[l-r^-vjf}

^a

9io

1-»„(«>'-*„)^{+(»'- »„) >T}

^-1

? (6 a)

-

^ [i-*,(•-*„)]•

und daraus

folgt

^sofort:

rtl «2 + _«x(</^-

v0)>^£(2)

^{+ a,(«' -}

»,)»22(2)

1 l

t d

= ffl «s +

as(v'

^-

v0)*^(l)

⁺

«,(»'

^-

v0f£^(h-

Die Glieder ax-a2, heben sich

auf,

^die

Gleichung

ist wiederum durch den Faktor

(»'

^—

v0f ^teilbar,

wodurch bewiesen

ist,

^daß die Gerade die Kurveim Punkte v ⁼ v0 oder v ^— oo

berührt,

also ebenfalls eine

Asymptote

^ist.

Wir wollen nun weiter

untersuchen,

wie die Verhältnisse sich

gestalten,

^{wenn das}

Polynom

X>P

^#

vom zweiten Grade

ist,

^{also etwa}

geschrieben

^{werden kann:}

Av* + Bv _{+ C.}

Wir

bemerken,

^{daß nun} zwei Glieder in der Gl.

(5')

^für

v = oo unendlich

groß werden,

^nämlich Av% und Bv. Wir führen "wiederum die Substitution ^{v —} —,

ein,

^wenden dasselbe Verfahren wie oben an. Setzen wir v = v0 in die Glieder

ein,

^die nicht unendlich

groß werden,

^so erhalten wir den Vektor

V0'

^{— C. Bilden wir nun diezu}

(6 a) entsprechende Gleichung,

^so finden wir:

+ b, 6i (»'^-v0y ^{' v'-}v0

+

-J-

(6b)

wo in der Klammer uns nicht weiter interessierende Summen¬

ausdrücke stehen. Erweitern wir den Bruch linker Hand mit

{v ^—

voy

und schaffen wir die Nenner weg, ^so

folgt

^nach

Weg¬

lassung

^{der sich} aufhebenden Glieder:

«i

h (°'-"o)

⁺ "i

(v'-vo)3l-

^•

•]

⁼ _«2

h ^("'- üo)

+ «a

(y'-«o)3 [•••]»

diese

Gleichung

^{ist also nur} durch den Faktor

(v

^—

v0) teilbar;

womit

gezeigt

^{ist: die zuA}

parallele

Gerade durch den End¬

punkt

^von C schneidet die Kurve imPunkte _{v'= v0} oder v ⁼ oo, aber berührt sie

nicht,

^sie ist also keine

Asymptote

^derKurve.

Würden wir dieselbe

Betrachtung

^{anstellen für eine}

Gerade,

^{die durch den}

Endpunkt

^{von C}

geht

^{und zu B}

parallel ist,

^{so würden wir}

finden,

^{daß sie die Kurve im} Punkte v' ⁼ v0

überhaupt

nicht schneidet.

Wir bekommen erst dann eine

Gleichung,

^{die durch den} Faktor

(»'

^—

v0)2

^teilbar

^ist,

^{wenn wir die Gerade durch den}

Endpunkt

des Vektors:

v ^- v0

parallel

^{zu A ziehen. Dieser Vektor wird aber selbst für}

v ⁼ v0

unendlich;

^{die zu A}

parallel

^{zu ziehende} Gerade würde somit _ganz ins Unendliche

fallen,

^{d. h. sie} wird selbst zur

unendlich fernen Geraden. M. a. W.: die unendlich ferne Gerade berührt die Kurve im Punkte v ^— v0

(o

⁼

oo)

^und

zwar

dreipunktig;

denn die Gl.

(6)

^{ist dann} sogar durch

(v— v0f

teilbar. Wir bemerken nun

aber,

^{daß die} Kurve im unendlich fernen Punkte v ⁼ w0 bzw. v ⁼ oo sich _genau so verhält wie die einfachere

Kurve,

die durch das

Polynom

^allein

-n-*+-B ^+c

^{bzw- Av2 + Bv +}

definiert ist. Denn die

übrigen

^{Glieder der Gl.}

(5')

^werden

mit wachsendem v immer kleiner und kleiner und für un¬

begrenztes

^v verschwinden sie ganz. Die

ursprüngliche

^Kurve

nähert sich also mit wachsendem v immer mehr der Kurve JU2+ ^Bv + C

und im Punkte ^{o =} oo haben sie die unendlich ferne Gerade

zur

gemeinsamen Tangente;

^woraus

folgt,

^{daß sie sich im}

Punkte v ⁼ oo selbst

berühren.1)

') Der Beweis dafür kann durch Einführung ^einer Substitution analog ^{wie bei der} geradlinigen Asymptote streng geführt ^{werden. Der} ebengeführteBeweis hat aber denVorzug^{derKürze und}Anschaulichkeit.

_ 24 ^—

Man nennt deshalb eine Kurve von der

Eigenschaft

^der

Kurve Av2_{-\- Bv +} eine

Nähertingskurve

^{oder auch eine}

krummlinige Asymptote

^der

gegebenen

^{Kurve. Ganz ent¬}

sprechende Betrachtungen gelten

^{für den}

Fall,

^{daß das}

Polynom

o

höher alsvomzweitenGrade

ist;

^es stellt immer eine

Näherungs¬

kurve für die

gegebene

^{dar. Wir werden}

sehen,

^{daß ein}

Polynom

^{zweiten Grades immer eine Parabel}

darstellt,

^ein

Polynom

^höheren

^Grades,

^{eine Parabel höherer}

Ordnung.

Diese

Überlegungen

^sind unmittelbar auf die

„mehrfachen

reellen Wurzeln"

übertragbar.

^{Für eine} mehrfache Wurzel erhält man nämlich durch die Substitution I ⁼

u)

eben- falls

Polynomen

^der

besprochenen ^Art,

^{so daß} man zusammen¬

fassend sagen kann:

Die

mehrfachen

reellen Wurzeln und der Wert v ⁼ + oc,

r

falls

^das

Polynom ~^»JPnvs ({>

^{> 1) höher als vom ersten Grade}

i)

ùt. bestimmen die

krummlinigen Asymptoten

^{der Kurve.}

Letztere sind

dargelegt

^{durch die}

Gleichungen:

r d

r=

yip

^{v? bzw. f=}

yi ^*«*

§ ^5.

Die Gerade als Ortskurve erster

Ordnung.

Wir haben bereits die Gerade zur

Bestimmung

^{der Ord¬}

nung einer Ortskurve benutzt und zwarin der

speziellen

^Form:

G ⁼

P+Qv, (2)

wobei wir bereits

bemerkten,

daß diese Gerade dadurch _ge¬

kennzeichnet

ist,

^{daß die} Parameterwerte auf ihr

„linear"

^ver¬

teilt sind. Diese

Eigenschaft

^{der Geraden G}

spielte

^{zwar bei}

der

Bestimmung

^der

Ordnung

^{der Kurve V} gar keine

Bolle,

sie ist erst dann von

Bedeutung,

^{wenn die}

Ordnung

^der

Gera.de

G

selbst

bestimmt werden

muß. Sol}

^{nun die Gerade G}

eine Qrtskurve erster

Ordnung darstellen,

^{so ist}

notwendig,

daß v linear auf' ihr verteilt sei. Denn nur in diesem Falle