ZARISKI CHAMBERS AND STABLE BASE LOCI
Volltext
where Σ P = Σ P0
Σ Q2
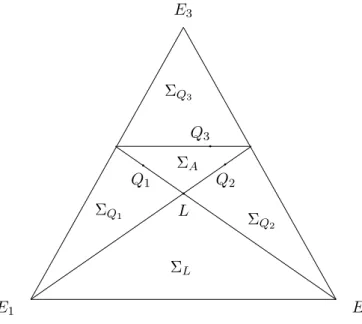
Figure 1. Two-point blow-up of the projective plane. The big cone con- sists of five chambers: Σ A , Σ Q1
• chambers Σ Q1
Abbildung
ÄHNLICHE DOKUMENTE
Additionally, almost all single indicators for option 2 showed larger satisfaction levels compared to the other two options, with the exception of solidarity, equity and
The aim of the BONN-IIASA Research Project is to analyse and forecast economic growth and economic structural change of Lhe most important countries (or groups of countries) in the
1) For some purposes it is too fast - the longest OPERATE cycle obtainable is 200 milliseconds, which makes readout on an X- Y plotter impractical. Also, many
1) Compared to CPY, most of the strains harbouring the D-Ldh gene, showed significant growth in D-lactate as well as three strains without the D-Ldh gene [significant growth at p
This argument is essentially correct, but with the reservation that from the statement (1) "There are judgements formed as a result of self-evidence but false" it only
(2009): Kohnen Station - the Drilling Camp for the EPICA Deep Ice Core in Dronning Maud Land.. (2007): Surface topography and ice flow in the vicinity of the EDML deep-drilling
Inexpediency of developments in the previous years of the monetary rule for the interest rate was explained by the lack of comprehensive reforms aimed at introducing
The modernization of the technical-material base in agriculture is a complex process which includes the expanding of engine uses, chemistry, the raising of high