Exercise sheet I

(1)

Quantenmechanik I – WS 06/07 – Prof. M. Gaberdiel

Exercise sheet I

Return: 7.11.2006

Question 1 [Compton effect]:

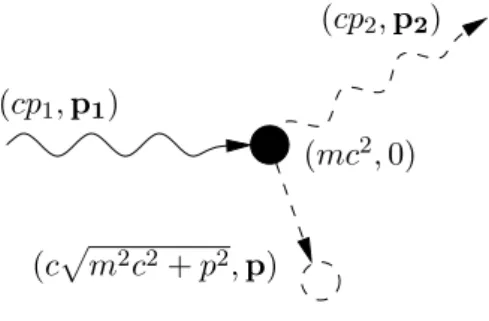
Consider the elastic scattering of a photon of energy and momentum (cp₁,p₁) off an electron at rest, whose energy and momentum are (mc²,0). Let us denote by (cp₂,p₂) the energy and momentum of the scattered photon, and by (cp

m²c²+p²,p) the energy and momentum of the electron after the collision. Since the scattering is assumed to be elastic, total energy and momentum are conserved. Under this assumption, show that

1 ν₂ − 1

ν₁ = h

mc²(1−cosθ), (1)

whereν_i are the frequencies of the photons before and after scattering,cp_i =hν_i, and θis the scattering angle,i.e. the angle between p₁ and p₂. The quantityh/mcis often called the “Compton wavelength” of the electron.

(cp2,p2) (cp1,p1)

(mc²,0)

(c^!m²c²+p²,p)

1

Figure 1: Schematics of the Compton effect.

Question 2 [Bohr atom ]:

Inspired by Rutherford’s experiments (1911), in which he showed that the atom con- sisted of a small, positively charged core surrounded by the negatively charged electrons, Niels Bohr in 1913 introduced his model of the atom, in which the electrons orbit the proton on circular paths at a radius r. The values of the orbital kinetic moment and of the allowed radii are quantized according to

mvnrn = n~, (2)

r_n = n²~²

me². (3)

(a) Use the De Broglie relation,λ= ^h_p, wherep=mvis the momentum of the electron, to show that

λ r_n = 2π

n , (4)

(2)

thus that the waves of the electron “fit around the orbit”,

(b) Show that the speed of an electron in a Bohr orbit is much less than the speed of light (thus demonstrating that it is reasonable to neglect relativistic effects).

(c) Show that the wavelength of light emitted from a Bohr atom (taking, for example, the transition from the orbit with n =∞ to the orbit with n = 1) is much greater than the size of the Bohr atom (which you can take to be the radius of the first Bohr orbit, the “Bohr radius”).

Question 3 [Galileo invariance of Schr¨odinger equation ]: Suppose that Ψ(x, t) is a solution of the time-dependent Schr¨odinger equation for a free particle, i.e.,

i~∂_tΨ(x, t) =−~²

2m∂_x²Ψ(x, t). (5)

Show that, for any constant u,

Ψ_u(x, t) = Ψ(x−ut, t) exp im

~

ux− im 2~

u²t

(6) is also a solution of the time-dependent Schr¨odinger equation.