Über den Verlauf des Drehmomentes bei asynchronen Drehfeldmotoren mit Käfiganker

Research Collection

Doctoral Thesis

Über den Verlauf des Drehmomentes bei asynchronen Drehfeldmotoren mit Käfiganker

Author(s):

Andronescu, Plautius Publication Date:

1921

Permanent Link:

https://doi.org/10.3929/ethz-a-000089690

Rights / License:

In Copyright - Non-Commercial Use Permitted

This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use.

ETH Library

über den Verlauf des Drehmomentes

bei asynchronen Drehfeldmotoren

mit Käfiganker

Von der

Eidgenössischen Technischen Hochschule in Zürich

zur

Erlangung

^der

Würde eines Doktors der technischen Wissenschaften

genehmigte

Promotionsarbeit

vorgelegt ^von

Dipl. Elektro-Ingenieur ^{Plautius N. Andronescu}

aus Bukarest

No.275 Referent: Herr Prof. Dr. K. Kuh 1man n

Korreferent: Herr Prof. Dr. P.

Debye

DruckvonRobertNoske,

Borna-Leipzig

Großbetrieb für Dissertationsdruck

1921.

Leer

^-

Vide

^-

Empty

/

Meiner lieben Frau.

Leer

^-

Vide

^-

Empty

*

Meinem verehrten Lehrer,

Herrn Prof. Dr. Ing. ^K. Kuhlmann,

bin ich für das wohlwollende Interesse und für den

gütigen Rat bei dieser Arbeit

zu

ganz besonderem

Dank verpflichtet.

Leer

^-

Vide

^-

Empty

/

Einleitung.

In der

vorliegenden

^{Arbeit soll} die Theorie des Drehmomentes

von

Asynchronmotoren

^mit

Käfiganker

^{behandelt werden.}

Die

nächstliegende Frage

^{bei der}

Lösung

^dieser

Aufgabe

^ist

folgende

^:

Welches ist der

Zusammenhang

^zwischen

elektromagnetischer Energie

^{und den} Induktivitäten in dem

Falle,

^{wo man es im Rotor}

nicht mit reinen Schleifen zu tun hat?

Ist einmal diese

Frage gelöst,

^{so kann man zu dem Problem}

des Drehmomentes

übergehen

und ist dann

imstande,

den Einfluß der

verschiedenen

Harmonischen des Feldes zu überblicken.

Auf Grund der entwickelten Theorie habe ich einen Ersatz¬

rotor

gebildet,

^der Schleifen besitzt und in seiner

Wirkung

^{mit dem}

Käfiganker gleichwertig

^ist.

Darausbildete ich die

Induktivitäten,

^und mit deren Hilfe wurde der Ausdruck für die

elektromagnetische Energie festgelegt.

Die Formel des Drehmomentes wurde daraus

abgeleitet.

Im weiteren soll der Verlauf des Drehmomentes in

Abhängigkeit

vom

Schlupfe gezeigt

^{werden. Diese,}

Frage

^{ist für die Praxis von}

großer Bedeutung,

denn beim Anlauf eines

Asynchronmotors

^mit

Käfig-

"anker kann es

vorkommen,

^{daß eine}

Sattelung

^des Drehmomentes besteht.

Durch

Beispiele

^wurde

gezeigt,

^{wie man solche}

Erscheinungen

verhindern kann.

Überblickt

man die

Literatur,

^{die eine}

Beantwortung

^dieser

Themata, bis

jetzt

^zu

geben

^versucht

hat,

^{so muß man} sagen, daß genaue

Erklärungen

^nicht

vorliegen.

Wie aus der Literatur zu ersehen

ist,

^{wurde der}

Jîafiganker

ⁱⁿ Deutschland vonDobrowolski erfunden. Darüber findet man schon im Jahre 1898 in

ETZ.,

^{S. 750 u.}

766, Angaben:

Rößler:

Über Stromverteilung

^imd

Energieaufnahme

^{von Kurz-}

schlußanker.

An dieser Stelle möchte ich noch

erwähnen,

^{daß die}

Beziehungen

zwischen

elektromagnetischer Energie

^{und Drehmoment}

(wohl

^eine

der

wichtigsten Grundlagen

^zur

Beurteilung

^der

Maschinen)

^{in der} Literatur sehr kurz behandelt sind.

Dieses Problem bildet für mein Thema die

Hauptaufgabe,

^und

dank der

Vorlesungen

^von Herrn Prof. Dr. K. Kuh 1m a nn konnte ich meine

Abhandlung

vollkommen auf die von ihm

gegebene

^Grund¬

lage

^aufbauen.

Die

Anregung

^{zu dieser} Arbeit wurde mir ebenfalls von Herrn Prof. Kuhlmann

gegeben.

Es war zuerst die

Frage

^zu

untersuchen,

^{ob im Falle des}

Käfig¬

ankers die Anzahl Phasen im Rotor für die

Grundharmonische

des Feldes

gleich

^{mit der Anzahl} Stäbe pro

Polpaar

oder pro Pol sei.

Aus der Literatur

ergab sich,

^daß die Stäbezahl _pro

Polpaar gleich

^{der Phasenzahl ist. In} dieser Hinsicht war die

Meinung

^von Herrn Prof. Kuhlmann

anders,

^{denn er} betrachtete die

Phasenzahl' gleich

^{der Stäbezahl} pro

Pol, gestützt

^{auf die}

Ansicht,

^{daß auch im}

Rotor eines

Käflgankers

^{mit Schleifen zu rechnen sei.}

Da nun pro Schleife

je

^{2 Stäbe}

nötig sind, ergibt

^{sich diePhasen¬}

zahl

gleich

^der

^Stäbezahl

pro Pol. Die

Aufgabe

^war

jetzt,

^{ein klares} Bild über solche Schleifen sich zu

verschaffen,

^{welche ich zu lösen}

versucht habe.

Erster Teil.

Aufstellung ^der Differentialgleichungen ^{für den} Käfiganker.

Bei der

Untersuchung

dieses Problems ist angenommen,

daß

der

Käfiganker

ⁱⁿ seiner Bauart

vollständig symmetrisch

^{ist. Der Stator}

besitzt

^{eine 2}

p-polige Dreiphasenwicklung.

Dabei ist

vorausgesetzt,

^{daß die} einer

Sinusfunktion

der Zeit verlaufen.

Statorströme

ia, ib, ic

^nach Es ist

Ja

⁼

Jb

^—

Je

^=J- Abb. 1 stellt schematisch einen

Käfiganker

mit m-Stäben dar.

fj fr i* J* ,i'j fi l>

^{Im tm-i}

<*? % "S °* ai «* ^«,.. ^

U U U u is i2 i«

Im

e, ^{e. e> e-.} es e2 e. Cm C"H

4. 4. ⁺

.

4. ^{4 A 4}

^$<m

a„.,

Irn-i

i» U Cs l* l's 1»

Abb. 1.

U Lm

Durch

Anwendung

^des

Induktionsgesetzes

^{in dem}

Falle,

^{wo das}

Magnetfeld

^rotiert

(Drehfeld),

^{erhält man durch}

Auswertung

^des

Linienintegrals/@da =/([ü ^{33] da)}

^{über die Schleifen}

(a^mb^), (ajbjbja.,)...

^{usw. die in den Stäben} induzierten EMKte ei; e2, e3...^em.

Dabei bedeutet o die

relative Geschwindigkeit

des Stabes gegen¬

über dem Feld und

93

die Induktion.

Unter

Voraussetzung

^der

Symmetrie

sind die Widerstände _rs aller Stäbe

a1b1, a.2b2,

^{...usw. sowie die}

Widerstände

_rr aller

Eingstücke

aj ajj,

\ \,

^{... usw. unter sich}

gleich groß.

In der

nachfolgenden Kechnung

^{ist der} Streufluß mit berück¬

sichtigt.

^{Es bedeutet}

^ls

^die Streuindaktivität des

Stabes, Ar

^des

King¬

stückes.

Unter

Benutzung

^{der Abb. 1 können wir}

jetzt folgende

^Be¬

ziehungen festlegen:

I.

Beziehungen

^zwischen

King-

^und Stabströmen.

i/^im'+ii V=imr+i1 + l2

i3'

⁼

im'-K+i2+i8 ^b) i8»=im»+i1+is+iil

im'=im'+i1+ii! + i3H h im im"=im"4-ii+i2+i3H hi«

Daraus

ergibt

^sich:

c) ia + i2 + ia

^-J

1- ^i,„

^{= 0.}

IL

Beziehungen

^zwischen EMKten: ex. e2, e3 ^{... em} Stab- und

Eingströmen.

Asdl('i_is) ⁺ rs,ii_i^+^^'W+ vAl'+^"]

⁼e*_e?

^ ^{(i,-is) + rs(i2-i8) +} ^(V+V) ^{+ r.(V+V)}

^-e2-e,

^^li8—U ^{+ rs(i8—i4) +} AId t(i„4-V') ⁺ rr(i3'+i3")

⁼e8-e,

b)

h j7 (im-

i

—im) + i"s(im-i —im)+hd~t ^(i'm -i+i"m-1) -fc- rr(i'm_ !+i"m-_i)

⁼em_i—e

Às^Ûm— ^{\) +rs(im—\)} +/.rd--(im'-fim") +rr(im'-fim")

⁼era—e^

2^(1/ ^{+ i2' + V H} hi."') +rrli1' + V + VH him')

⁼⁰

^r/t (i/'-f- i,"+ i8"+

^•••

+ im") +

^rr

oy+ i2"+ i3'H {- im")

^=0.

Die Summe

V + V+V+•+!.»'

^bezw.

i/' ⁺ V' + V'H him"

läßt sich aus den

Gleichungen

^{I in Funktion der} Stabströme schreiben:

V + i,' + i,H h ^im'

^=m

im' +

^m\

+ (m—1) ^i, + (m—2) i3 +

^•••

-f (m

^—

^(m— l))im

ii"+ V'+ h"-\ h ^im"

^=m

im"+

^m

i, + (m—1) i, + (m—2) i, +

^••

+ (m—(m—l))im.

Man erhält somit für die

Gleichungen

^IIb

folgende

^Ausdrücke:

4^(mim') ^{+ rr(mim')}

⁼

—Ar^fmijH ^{1- (m— (m—l))im]}

—rr

[m^-l

^k

(m— (m—l))im]

Ar^(niim")+rr(mim") =—A,.^ ^{\m\-\ 1- (m—(m—1)) im]}

—

r^mi^ (-(m—(m—l))im]

^.

Daraus läßt sich

erkennen,

^daß

im'

⁼

im" ist,

^{und aus den}

Gleichungen

^I

ergibt

sich weiter

ia'

⁼⁼

ij^'% i2'

⁼

i.2",

^{. . . usw.}

Die

Differentialgleichungen

^IIa lassen sich dann schreiben:

. d .

/sdt( ⁱⁱ

^—

^{h) + rs(ii}

^—

^{h) +} 2;''(ftii' ^{+ 2r''V}

^{= ei— e2}

isdt(i* ~~is) ~^~ Ts{i* ~~is> ^~ 2Ard t*2' ^{^~ 2rri*'}

^=e2—e«

^dt(im—it) ^{+ rs(im}

^—

^{\) -f-} 2ir^im' ^{+ 2rrim'}

^{=em—e^}

Diese

Gleichungen

^{enthalten neben den} Stab-EMKten und Stab¬

strömen auch die

Ringströme.

Um die

Beziehung

zwischen den Stab EMKten und Stabströmen allein zu

ermitteln,

^{muß man die}

ßingströme

^aus

obigen Gleichungen

eliminieren.

Wir benützen dazu die

Gleichungen

^{Ia und IIc. Unter Zuhilfe¬}

nahme

dieser Gleichungen

^{kann man die}

Eingströme

^{aus IIa elimi¬}

nieren,

^{und somit}

ergeben

^{sich für die}

Beziehung

^{zwischen Stäb-} EMKten und Stabströmen

folgende

^Ausdrücke:

III.

^itÜi- i,) + r,(i,

^—

y+ 2^-^ ⁺ 2^

—/r-r-lm^H

Min—(m—l))im] ^— i

m d tl ^{y 'ii} m

^d^(i2-i8) + r3(i2-iï) + 2Ard^(i1+i!!) ^{+ 2rr(i1 + i2)}

~m"rdtlmi]~i l-(m-(m-l))im]-inrr[.--]=e.2-e$

^^(i3 ^{—i4) +} rs(i3—i4)'+2Ar^t(i1 ^{+ i., +} i3) + 2rr(i1+i.2 + i3)

~mArdtlmilH ^h (m-(m-l))ira]-mrr ^[••]

⁼

4;n:(im

—i:i) + rs(im —ij+

^O

+

O

sdtv

_

m

Àl'dt'm^ ^{"I ^} (m—(m—1))im]

^—_m^rr

[

^{• •}

j

^==em—e,.

Diese

Gleichungen

lassen sich noch etwas

umformen,

^{wenn man}

von

je

^zwei

Gleichungen

die Differenz bildet.

Man erhält somit als

Endresultat

für die oben

genannten

^Be¬

ziehungen:

IV.

^ä+Gi- ^{2i-2 + i3) + rs(ii}

^—

^2h+h)

^—

2^t ⁱ²

^—

2rri2

⁼ e1^—

2e2 +

e3

^^2

^—

2i3+iJ + rs(i2

^—

2i8 + iJ

^—

2^^

^—

^2rri3

^=e2—

^2e3-fe4 4^(i3 ^{—2i4+i5) + rs(i3} —2i4+is) —2xr--i4 —2rri4

⁼e3

—2e4 +

ef)

isdl (i4-2i5+y + rs(i,-2i.->+i(i)

^-

2;vrAi5 _2rri5

⁼

e4-2e5 +

es

As^(im_i

^—

^{2im + ij) -)-rs(im_i}

^—

^2im+y

^—

2Xr-^im

^—

^2rrim

= em„i^—

2era-f

et.

Die

Gleichungen

^{Ic und IV}

geben

^ein

System

^von m-Differental-

gleichungen

^mit m-Unbekannten

ix, i2, i3

^{. . .}

^im.

Um diese

Differentialgleichungen

^{lösen zu}

können,

^{wollen wir}

uns zuerst an

einige

mathematische Sätze erinnern:

"Wennmanzwei

Differentialgleichungen

^{von kter}

Ordnung

^{in i hat:}

dki dk~xi di

ak^ ⁺ ak_1^_T ⁺

^....

⁺ a1(ft ^{+ a0i}

^=A

wobei ak, ak_i,

bk, bk_i,

^{. . .}

Konstante, A,

^B

hingegen

^Funk¬

tionen der Zeit

sind,

^{erhält man durch} Elimination ^von:

dki dk-xi

. . l

dtk' dtk"!

eine

Differentialgleichung

^{von ktei}

^Ordnung

^{in A und B:}

dkA .

dk-xA

. . dA . . ,

akdtk ^{^ K_1}

dt*-1

^{^ ' 1} dt

.dkB,Ä dk-!ß ^XJB

*de + /,k dtFï +

^{" -}

+ ßi1I ^{+ ßo*}

^=0-

wobei _{ak, ak_i,} . . . .,

ßk. ßt-i

^{.... Konstante sind.}

In unserem Falle haben wir

m-Differentialgleichungen

^:

., „

/di1 di„ dim

^{. . .}

\

...

11

'(dt' dt"---"ÎT'

^'"

•••••-)

⁼

^«•.('»

.

/d^ di2 ^dim

^{. . . \}

Durch

Elimination

von

ij

^und

-rf

^{aus 1 und}

^2,

^{1 und}

^3,

^{1 und 4}

. . .. 1 und m erhält man

(m—1)-Gleichungen

^2.

Ordnung

ⁱⁿ

i2, i3,

h ^....

im.

Durch Elimination von

i2

^{und -~ aus den neu}

gebildeten

^Glei¬

chungen

^{erhält man}

(m—2)-Gleichungen

^3.

Ordnung

ⁱⁿ

i3, i4, i5

^...

^im

und endlich durchElimination von

im_i

und ^—-

ira-i

^{erhält man eine}

dt

Differentialgleichung

^{von mter}

Ordnung

^von

im

_

dmim dm-xim dm-2im dim

+am-i _..„^ ⁺am-2 ^,tm_2

H h_ai-^r-

+

a0im⁼

<p(t),

m dtm ^' ""-'dt"-1

'

m-*dtm-2

' ' xdt

wobei am, am-i, ^{• • • •} a0 konstante Größen sind.

Analog ergibt

^{sich für}

jeden

^{der Ströme:}

ii; ^1,

^....

je

^eine

Differentialgleichung

^{von mter}

Ordnung.

Wenn e1, e2, e3 ^{. . ..em} Sinusfunktionen der Zeit

sind,

^{dann ist}

q>

(t)

^eineSinusfunktion, und somit sind \,

i2, i3

^{... .}

^im

^im

Beharrungs¬

zusstande auch Sinusfunktionen.

Es sei angenommen:

et ⁼

E,/,

^{sin cot}

e2 ⁼

E<p

^sin

(cot

^—

ß)

e3 ⁼

E<psin(t»t— 2ß)

em⁼

E</>

^sin

(cot— (m—l)ß),

wobei

ß

^— p^•--

m

i,, i.2, i:,

^{.. . .}

^im

^{werden von} der Form sein:

ix

^{= Jsin}

(co

^t—

(p) i3

^{= Jsin}

(co

^t—c/'^—

ß) i8

^—

Jsin(cot

^—cp^—

2ß) im

^{= Jsin}

(cot

^—cp—

(m—\)ß)

Gesucht werden _{J und q.}

Aus den

Gleichungen

^{IV kann man die} Unbekannten J und _cp bestimmen. Wir hatten:

Asdl(il

^—

^{2i2 + y +} rsk—2i.2+i8)

^—

2Ardti*

^~~

^{2Tt^}

^{=ei ~ 2 e2}

⁺

^es

Für e1^—2e„

-f- e;J

^{hat man:}

e±^—

2e2-)-e8

⁼

E</>(sincot—

^{2 sin}

^(cot

^—

^{ß) -\-}

^sin

^(cot

^—

2ß))

=

E*(2cos/?sin(cot

^—

^ß)

^—2sin

^(cot

^—

ß))

—

E</,

sin

(co

^t—

ß) (cos ß

^—

1)

=—

4EfJ5sinä^ ^sin(cot

^—

^ß).

Li

Analog

^{erhält mau für} \^—

21,-j-i3:

\ ^—

2i2 --(- ig

^{= —}

4Jsin'2(j ^sinfcot

^—co—

^ß).

Setzen wir diese Werte der

Spannungen

und Ströme in

obige

^Diffe¬

rentialgleichung ein,

^so erhalten wir:

—

4coj;tgsin2£

^{cosfcot—cp—}

^ß)

^—

^4Jrssin'2 £

^sin

^(cot—

cp^—

ß)

—2co

J?.r

cos

(cot

^—cp^—

ß)

^—

2Jrrsin(cot

^—_cp^—

ß)

=^— 4

E<£

^sin2

'1-

sin

(cot

^—

ß)

Jco(2Assin2^--j-^r (cos (cot—q>—/?)-{- J|2rssin'2 ^{~-|-rr 1}

^sin

(cot—cp— ß)

^„

=2 E_$sin'2^~sin

(<»

^t—

/J)

^.

Aus dieser

Gleichung ergibt

^{sich J und}

tgc«,

^{wenn man z. B.}

cot^—

ß

⁼q und cot^—

ß

^{= 0 macht.}

Für mt^—

ß

⁼<p hat man:

E^.2sin2^sinç5

T Li

24sin-g ^-f-

^{/, |co}

für cot ^—

£

⁼⁰

co

(2/ssin2 ^{-)- Ar} jcosc/

⁼

(2rçsin'2^ ^-f~

^rr

J ^sin90.

Daraus

ergibt

^sich:

col2;.ssin^ ⁺

^/

tg^

^{=- —}

2rssin2' -f-

^rr

co2(2/,sin^ _{+ Â}

• 1

tg <P \ 2

sm2(p^{= ö ^ — x}

1

+ tgV /2rssin2 ^ ⁺

^rr

^{Y +} w^^sin» ^{| + Ar}

Durch Elimination von sin_cp aus der Formel von J

ergibt

^sich:

J⁼

E*.2sins§

|/(2r,sin8^

^-t-

^{r,)2 +} ws(2Â3sins| ^{+ A,}

Was hier an dem einen

Beispiel

ausführlich entwickelt

wurde,

ist nun in dem

Fall,

^wo elf e.2 ^{.... em} ganz

allgemeine periodische

Funktionen der Zeit

sind,

^ähnlich

durchzuführen,

^indemmane,, e2 em in eine Fourriersche Reihe

zerlegt.

Für die weitere

Behandlung

^der

Aufgabe

^scheint zunächst eine

Schwierigkeit

^{darin zu}

liegen,

^{daß wir es im Rotor mit keinem}

Schleifensystem

^{zu tun}

^haben.

Um die

Umsetzung

^von elektrischer

Energie

in mechanische be¬

urteilen zu

können,

^{müssenwirdenAusdruckfür die}

elektromagnetische Energie aufstellen.

Dafür hat man

folgenden allgemeinen Ansatz,

^{der sich aus den} Stator- und Kotorströmen sowie den Selbst- und

Gegenseitigen-In-

duktivitäten aufbaut:

1 k=m 5.⁼n

ü⁼ _9ü

2 ^{2 iki;.L/.k-}

k=l /.=1

t

Zweiter Teil.

Bestimmung ^der Induktivitäten.

Es ist zuerst nicht

leicht,

^{sich von dem} Vorhandensein der

Rotorinduktivitäten

eine klare

Vorstellung

^zu verschaffen.

Am einfachsten läßt sich die

Aufgabe lösen,

^{wenn man den}

Käfiganker

^{durch ein}

Schleifensystem ersetzt,

^{welchesinseiner}

Wirkung

dem

Käfiganker

vollkommen identisch ist.

Abb.2.

Die

Wirkungsweise

^dieses

Ersatzspulensystems geht

^{aus der} schematischen Abb.2 klar hervor.

Es sei die Anzahl der Stäbe m= 6.

Alsdann hat man 6

Spulengruppen

^{zu bilden:}

Andronescu. 2

Spulengruppç

1 besitzt 2

Schleifen,

ⁱⁿ welchen die Ströme

it

^u.

^im' fließen,

Li „ O _{,. ,. „} „ „ lj, lg ^{U. lm „}

3 4 i i

6

DasGesetz vom

magnetischen

^Kreis

§!q

^{do für}

irgendeinen Weg

z. B.

(a)

^{Abb. 2 ist identisch mit der}

magnetischen Wirkung

^des Stromes

i5

^allein.

Ebenso das Gesetz der

elektromagnetischen

^Induktion

/@do=/([o©]da)

behält seine

Gültigkeit.

Auf diese Weise können wir die Selbst- und

gegenseitigen

^In¬

duktivitäten des Rotors bestimmen.

Wir

zerlegen

die Induktivitäten in 4 Teile:

1. Die Selbst- und

gegenseitigen

Induktivitäten des Stators allein

L^k,

wobei ^A=_a,

b,

^{c k=}a,

b,

^c.

2. Die

gegenseitigen Induktivitäten,

^{die sich auf}

gegenseitige Wirkung

^von Stator und Rotor beziehen

M;k,

wobei l⁼a,

b,

^{c k=1 : m.}

3. Die Selbst- und

gegenseitigen

Induktivitäten des Rotors allein

(Die Streuungsinduktivitäten

^erster

Ordnung

^nicht

inbegriffen.)

wobei A⁼ 1 : m k=l-^m.

Auf S. 15

ergab

^{sich aus der}

Beziehung

^{zwischen Strom J und}

Spannung E,p

^{als effektiver Widerstand und effektive}

Streuungs¬

induktivität:

und

2sm2|

²

sin3|

Wir können somit für die Rotorstreuinduktivität den Ausdruck

2

sin21

^einsetzen.

Für die

Bestimmung

^derInduktivitäten ist angenommen, daß ^im ganzen Raum des

Spulensystems,

^diePermeabilität u dieselbe ist und

somit das Feld mit der

MMK (magnetische

^Umlauf

Spannung)

pro¬

portional

^wird.

Das Feld nimmt

infolgedessen rechteckige

^{Form an.}

Unter dieserAnnahme sollzunächst untersucht

werden,

^wiesich die Induktivitäten von zwei

Spulen

^von

beliebigen

^Breiten

verhalten,

erstens in

bezug

^{auf die}

rechteckigen Felder,

^{zweitens in}

bezug

^auf

die Harmonischen des Feldes.

Man denke sich im Stator und im Kotor

je

^eine

Spule

^mit g±

bezw.

e'x Windungen. (Abb. 3.)

Es sei i⁼i'⁼ 1

Amp.

b;

SUIorumtôn

M-

b:

b RotorumMrig

Abb. 3.

Wir haben dann eine

magnetische Umlaufspannung (in Gauss-cm)

im Stator MMK⁼4.T

-^

^gt

im Rotor MMK ⁼_v?r Q\- in

10

In

bezug

^{auf den}

Ankerumfang

^{teilt sich die MMK für den}

Stator in

4:71 b

für den Rotor in

471 a ,

ïëfc2nnd

47t ,a'

10 ^-1à ^'

wobei AB ⁼ a

ÄJB'

⁼ a'

BC ==b

WU=b'

AC

⁼

A'C

^=A

Umfang ^{des Ankers}

^bezw.

^{Stators. Für}

^ein

^Flußrohr

2*

von

Querschnitt

1 und magn.

Permeabilität

_n⁼ 1 und

Länge

^{=d er¬}

gibt

sich ein magn. Widerstand ⁽⁵

cm/cm'2.

Die Induktion B wird

am

Statorumfang

^ttcQ'~ä t^—

&i

am

Rotorumfang tö-Si'

_-j ^t=

Bi'

ioei2"a~~

^B»"

Wir können somit schreiben

für

das

Statorfeld B⁼

ît (a0)

für das Rotorfeld B'⁼

tj (a0)

a0⁼

Bogen,

welcher für _a0⁼A=2n wird

«oi=^-a

^{und «oi}

=^"a ⁽²ⁿ

^—

«oi)=-Xb-

Die

Zerlegung

^der

rechteckigen

Kurven in ihre Harmonischen läßt sich mittels der Fourierschen Reihen durchführen.

Nach Fourier hat man

B ⁼

B0 -f ^ ^(Bsh„

^sin

^h0

^a0

^{-f Bch„}

^cos

^{h0 a0),}

h„=l

wobei

BSb0

^und

Bei><)

^die

Amplituden

^{der Sinus- bezw.} Kosinuslinien der

ho*611

Harmonischen des Feldes bedeuten.

Dabei ist

h0

^eine

gerade

^oder

ungerade

^•Zahl.

Bn

⁼

^ J ^B2da0— J ^Bid«,,

B,

_sh„

B,

ch«

1_

71

1

71

2n

sin

h0

a0 d a0

j ^B2

^sin

h0a0äa0—j ^Bt

0 _«Ol

«oi 2:rr

,

I

B2 cosh0a0da0—

^l

Bx

^cos

ho^da,,

In unseremFall

ergeben

^{sich für}

B0, BSh„

^und

Bcho folgende

^Werte:

B»

⁼

^[B4Si ⁺ BiKi-2«)]=-^[B,(o„l-a«i)]-0

ßsh„

Beb,,

1

Jl

1

71

1

7rh0

1

TT

j-1 (1

^—cos

h0 «01)

^—r~

^{(cos h0}

a01 ^{— cos}

h0

²

«)

"0 "0

(B, + BJ ^

^-

^{(B2 + BJ A-} _h0

^cos

^hu

^«01

ÏOQïô ^{1

^cos

^{h0 a01)} (B2 + Bx)

^{r- sin}

h0

uä

"o

1 4tt 1 . ,

Wir können somit für B

folgenden

Ausdruck schreiben:

B⁼

Bsi

^sin _a0

-(- ^Bei

^cos a0

-\- BS2

^sin

2a„4- ^B02

^cos 2 «0

-(-

4 ^{. . . .}

-)-... ⁺ Bsh„

^sin

h0

a0

-f Bcho

^cos

h0

a0 -4- ^{. . .}

wobei das

allgemeine

Glied dieser

trigonometrischen

^Eeihe

BSb0

^sin

h0a0 + BCb„

^cos

h,,

a0 inunseremFalle sich in

folgender

Weise schreiben läßt:

1 \ji 1

Bsb(1

^sin

h0a0 -f Bcb„

^cos

h0

a0⁼

-^ -^Ql

^-

^{[sin hc}

^{u0-4- sin}

^{h„ (a0l}

^—

^«„)]

Aus dieser

Gleichung

^{ersieht man}

sofort,

^daß für a01 ⁼0 oder k^•2Ji

(k

eine ganze

Zahl)

keine Harmonische

existiert,

^{und für} ani ^{= n}

1 4tt 1

ergibt

^{sich —} _{-p- qx~}

[sin h0a0

^—sin

h0a0

^cos

h0;i],

^{wobei für}

h0

⁼

gerade Zahl,

der Ausdruck null

wird,

^{und für}

h0

^=li=

ungerade

^Zahl

hat man —=- ^r^o,~ sin

h„

^{an ein bekannter}

Ausdruck,

der sich ^er-

7ia 10 ^'o ^u

gibt,

^{wenn man die}

Spulenbreite gleich

^{n annimmt.}

Analog ^erhält

^{man für die}

hftte

Harmonische des Rotorfeldes 1 4n 1

B's

_ho^sin

h0

a0

-f B'c

,,0^cos

h0

aa^{= —}

-^ o,'- ^sin h0

a0^-J-sin

h0 (a'01

^—

«„)].

Jetzt soll bewiesen

werden,

^{daß die}

Gleichung M1X'

⁼

M^

^für

die

rechteckigen

^Feldersowie auch fürdie

entsprechenden

Harmonischen des Feldes

gilt.

Für die

rechteckigen

^Felder

ergibt sich,

^{wenn man}

Mu'

⁼

M1'l bildet,

BBa'e1'

⁼

(Bt'a'-B1'(a-a'))e1.

Setzt man die Werte von

B2, B2', B/

^{in die}

Gleichung ein,

^dann erhält man

4» b 1* _{, ,}

4ji,b'l,

^4sr

,a'

¹ ,

ïo^i^^-ïo01 Jda

^ffl

~ÏO~01 Jä(a

^~a)Ö1

4tt b 1 _{, ,} 4ji

,1

, 4ot

,a'

¹

iö-ei7äaffi

^-

ïô*i ä

^{a ft -}

ïoe* 2

* ai?1 4tt b 1 _{, ,} 4ti

,1

, / a\ 4ti

,1

, b

was zu beweisen war.

Wenn man

Mj°,

⁼

MJ1,01

^setzt

^(wobei MjJ,

^die

gegenseitige

^In¬

duktivität der

h0ten

Harmonischen des Feldes

bedeutet),

^{so erhält}

man

analog

, «Ol' A p ^'

— I

(Bsho sinh0a0-f Bcho cosh0a„) dag/

«oi

*

—

/ _(B'sho

sin

h0

a0

+ B'cbo

^cos

h0

_a0

) da0

6l.

0

Das linksstehende Glied dieser

Gleichung

^{kann man in}

folgender

Art schreiben:

2?l(

«Ol

/

^—

~^Ql ^{-(sin h0a0 +}

^sin

^{h() (a01}

^—

^{a0)) d«0 q,'}

0 ^"o

==

2^ ^i" Jo"

^ft

Qi'jI1

^—cOs

^{ho «oi' +}

^{cos üo}

^(«oi

^—

^«oi)

^—cos

^K«oi]

=

Mh°

Das Glied rechts wird A f«i ^{1 in} , 1

2 Ö

^1 ~T^?i'l(sin h«ao +

^sinflo

Ki'

^—

«o) ) d«o

ft ^~

-

^~ä jq^ ^ft' ftj[

^!—COS

^{h0 a01.-f}

^COS

^{h„ (a01'}

^—

^a01,)

^—

^C0sh0

^a„

=Mb°

mi'i

Daraus ersieht _man, daß die

obige

^Annahme

berechtigt

^ist.

Nachdem wir

gesehen haben,

wie sich die

Induktivitäten

von

zwei

Spulen

^von

beliebigen ^Breiten verhalten,

^{wollen wir}

jetzt

^die Stator-Induktivitäten bestimmen:

L;k

^{für l=}a,

b,

^c; k⁼a. b. c.

w

H

0-9-9- ^0-0-0" *-"9"Y"S>

û Sratorumfan?

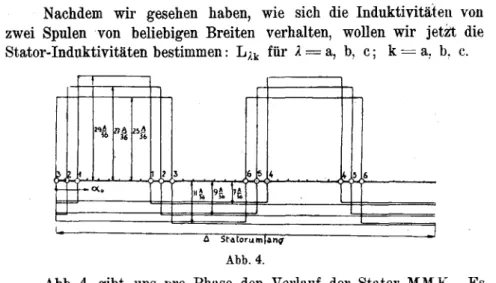
Abb.4.

Abb. 4

gibt

^uns pro Phase den Verlauf der Stator-MMK. Es sei

angenommen

2 p ⁼

4,

^{q = 3}

(Anzahl

^Nuten pro

Pol

und

Phase).

Wir haben somit im Stator 36 Nuten. Die

Leiterzahl

_pro Nut in Serie _{sei qv}

Die

MMK, erzeugt

^{vom Strom}

ia

^{in der}

Spule

^1—

1,

^{ist A =}

in .

iö

^{la Ql"}

Mit Rücksicht auf den Verlauf dieser MMK am

Umfange

^wird

A in zwei Teile

geteilt

SV UDdâ29-

Analog

^{werden wir} die MMK der zweiten

Spule (2

^—

2)

und der dritten

Spule (3

^—

3)

^{ebenfalls teilen in}

à9

^und

à27

All

und

A25.

Die

Superposition

^von allen drei MMKten

gibt

eine resultierende'

MMK,

deren Verlauf in

bezug

^{auf den}

Umfang symmetrisch

^ist.

Abb. 5

zeigt

^den Verlauf dieser res. MMK.

Bezüglich

^des

symmetrischen

^{Verlaufes dieser res. MMK. kann}

man sie entstanden denken durch

folgende Verbindungen

^der

Spulen¬

seiten

(3

^—

1), (2

^—

2)

^und

(1

^—

3), ^wobei

die MMK einersolchen

Spule

in Funktion des

Ankerumfanges gleich

^{•=- sein muß.}

Man denke sich ein

bewegliches Spulensystem (1, 2, ³⁾

genau wie das

erzeugende ^(im

Felde des ersteren

beweglich), wobei,

^{wie wir}

Verlauf des

ae<re.mei(iqen

IndaKtivilchKoeU als \w*XU*w 'map*

Abb. 5.

Abb.6.

wissen,

^es'

gleichgültig ist,

^{wie die}

Verbindungen

^der

Spulenseiten

ausgeführt werden;

^dann

^erhält

^{man für eine}

beliebige Lage

^des

zweiten Spulensystems

^{den Verlauf der}

gegenseitigen Induktivität

zwischen dem ersten und zweiten

Spulensystem gemäß

^{Abb. 5.}

Der Verlauf der

gegenseitigen

Induktivität wurde in der Art

festgelegt,

^{daß man für}

jede Spule (1

^—

1), (2

^—

2), (3

^—

3)

^{die Summe} der

Quadrate

^{des karrierten}

Papiers gebildet hat,

welche Summe als Maß für den

Fluß,

der durch die

Spule hindurchgeht,

^zu betrachten ist.

Für die weitere

Behandlung

^des Problems ist es

zweckmäßiger,

das Feld in seine Harmonischen zu

zerlegen

und die Induktivitäten in

bezug

^auf die betreffende Harmonische des Feldes zu bestimmen.

Es sei für

ia

^{= 1}

Ampère

IÏ^

^{= B-}

^(Abb-6)

Wir

zerlegen

^{B in} seine Harmonischen

6⁼

6!

^{sin a!}

-f B8

^{sin 3 a'}

-+- B5

^{sin 5 a!}

-\-

^{. . .}

-f Bh

^{sin ha'}

+

^{. . .}

B⁼

Bx

^sin

(a'

^—

y) -f B3

^{sin 3}

(a'

^—

y) +

^...

+ Bh

^{sin h}

(a'

^—

y) -f

^{. . .}

8⁼

6!

^sin

(a'

^—

2y)-f B3sin3(a'

^—

2y)-L...+Bhsinh(a'

^—

2y)+

^...

B^Bi

^sin

(a' ^{—(q —1)} y) ^{+ B8}

^{sin 3}

(«'

^—

^(q

^—

¹⁾ /)+...

-f Bhsinh(a' —(q —l)y) +

^...

Dabei bedeutet h eine

ungerade

^Zahl.

Die hteHarmonische des resultierenden

Wechselfeldes

für

ia

⁼

1

Amp.

^sei

93ah

SBah=Bh[sinha'-i-sinh(a'—y) ⁺ siQh(a'—2y)+...4-sinh(a'—(q—l\y)l

sin h

Bh-

-. ~sin^y

h(a'-(q —1)£)

sm h ^~

tiYl ^'

2 f 4

wobei

Bh

^{= -} I B sin h a' d a' = B jiff

0

Es sei a=a'^—

(q

^—

1)

^{7 .} Dann erhält man

sin h

S3

ah⁼

Bh

^{—sin h « .} sin h „

In der

gleichen

^Weise

ergeben

^{sich für}

ia

⁼

ib

⁼

ic

^{= 1A} die hten Harmonischen der res. Felder der Hten und IIIten Phase zu

. sin h _{ö / a ,}

S3bh=—r-B

sin h a^—

Q sin h ^'

. sin h _-s

4 . 2

Soh

⁼_-t:B ^—sin h

Tth . , y

sm h ^'

(-«•£)

a' bezw. a sind elektrische

Winkel,

^{denn sie} beziehen sich auf den

^ten Teil des

Umfanges.

Der räumliche

Winkel

ist _an⁼—.

P

Mit Hilfe dieser Harmonischen der Felder kann man

jetzt

^die Induktivitäten

Lh

,

iA

,

Lh

bestimmen. Die Ankerlänge sei ⁼ 1^•

aa^' ab^" ac °

u^

. sm hV

Th ^{r 4 2}

-L'a. ⁼ Qi ^ü B

sm h ^

JT-(l-l)|-+2

.t-(h-I)-!

*-<q-i)-|

^{+ r}

/

sin hada

-\- ⁱ

^{sin hada}

-ta-«',

(q-i)-|

⁺⁷

-T+(q-l)-5-

-j-

^{i sin hada}

-| |-

^{I sin hada}

-(1-1)

1+23'

(q-1)

l

Man hat

—

(q —1)

⁼

d-q)

₂

.(q —l)£+y

⁼

(3-q)£

_-(q_l)| ^{+ 2y}

⁼

(5-q)|

(q—1)

^Y

((2q-l)-q)|

Wir können somit schreiben:

sin h _^r-

•

t 4 „ 2

,-B-

sin h

^

yq

:i4-(l_q) ^-T t-((2q-l)-q)-l

l sin ha

da-| j-

^{I sin had«}

<i-<i>i ((2q—l)-q)

_1'V

. sin h _

,

t 4

._, 2 . lui

^ 7i\v jih . , y 2

sin h jj-

Li

sinh(^+(l-q)|)

T 4

Tl

sm h ^Se

+ sinh(2+(3-q)|) ⁺ sinh(j ⁺ (5-q)|) ^{+ ...+} sinh(|+((2q-l)-q)^

in h

(J ⁺ #)+••

^.

⁺ smh(j ⁺ #+(q-l)y)

2 _„ . hjr

, ^-

—2 sin-^r-

jrn Jill . , y ^Z

sm h ⁼

Li

yq

. sin h

t 4 2 . hTi

=q± ^--,—rB 2 sin

sin h 2 .

7i\i jrh

sin h _s 2 •

i y

sin h

^

sin h Wir erhalten somit:

Laa

^=Öl ZS« ^T B

sin h j'q

sin h

^

2 » . , 71 . - 71 sin h sin h

Li Li

In

gleicher

^{Art werden}

Lab

^und

Lae

^ermittelt:

yq^

b ; sin h

o .

L"v_ab=0-,_tl —rr„ ^t B

st* h

^-^

^tB

sin h

sin h _^ sin h

Li

sin h

sin h

7Q_

smh2Smhl2+2

3

/

sin h wobei et -jT-j ^t B

sin h

2 i . .T sin h _

}' ^{/ 2}

L"

ist.

m

Wir können somit für eine

Spule k,

die genau wie die Stator¬

spule gebaut ist,

^die

gegenseitige

Induktivität für die hte Harmonische des

Feldes

in

folgender

^{Art schreiben:}

L:k

⁼

^^(h(« ^{+ ^ +} ,k-a,h^j

=

Lhmsin(h(« ^{+ ^-^) +} «k_a)h^)

(h(a+2-2¥)+^h¥)- 'ck=^m Sln| n(«

⁺

^

Dabei

hat man a^—a⁼

0,

^b—a—

1,

^c•—a=2.

Bekanntlich ergibt

^{sich durch}

Zusammenwirken

von allen drei Phasenströmen des StatorseinDrehfeld und auf Grund dieses Drehfeldes kann man eine Drehinduktivität

bestimmen,

^{welche die}

Beziehung

zwischen

Drehfluß

und Phasenstrom darstellt.

Die Wechselfelder von allen drei Phasen des Stators _a,

b,

^c

lassen sich in

folgender

^{Art durch zwei}

gegenläufige

^{Drehfelder von}

halber

Amplitude

ausdrücken:

Das

Wechselfeld

von Phase a sin h

S3(ah) ^Ja

sin »i t^{= t} BJ sin h

JLI

72

^cos

^(ajjt—ha)

^cos

^{(w1t -f- ha)}

das

Wechselfeld

von Phase b ^•

/

2n\

ⁱ

23(bh) ^Jb

^sin

^o),

^t

çrj

^—

^

^{B J}

sin h 2 1

sin h ⁷ 2 ^{COS CO}

2n

J 2n\\

,ït___h(a___)j

COS

j

^{ö>± t}

^;+ >(-£))

das

Wechselfeld

von Phase c

33(oh) Jb

^sin

(a^t

^—2-

_{-jH= -^}

^{B J}

sin h

^

2 1 sin h ⁷ 2

cos

|ö>it_2.^-h(a-2-^)j_cos(«>1t-2.^+h(«-2.^))

Das Drehfeld entsteht durch

Superposition

^{von allen drei Wechsel¬}

feldern.

Die Summe aller Cosinus-Ausdrucke wird

cos

(û^t—ha) + cosl (Ott—ha -(--^ ^(h—1) ]+ ^{cos( a^t—ha -j-}

^2~

^(h

^—

¹⁾ j

—

cos^t-f- ^ha)— cos( _ft^t-j-

ha—

^(h+l)l—cosla^t-j-

^ha—2-

^-«-(M" 1))

r=

(— lp

^{+1 3 cos}

(cott + (— l)n

^h

a),

wobei n eine

gerade

^oder

ungerade

^{Zahl sein kann.}

Es istzu

beachten,

^{daßfür h= 3}

(2

^n—

1),

^wobein=

1, 2,

^3•• ao, das resultierende Drehfeld

93jh

^null

wird,

^{wobei h stets}

ungerade vorausgesetzt ist;

nur für h⁼ 1

-\-

³

⁽ⁿ

^—

^1),

^{wobei n=}

^1, 3,

^{5-•• oo}

(ungerade Zahl)

oder h^—5

-f-

³

⁽ⁿ

^—

^2),

^{wobei n=}

^{2, 4,}

^{6-•• oo}

(gerade Zahl) gibt

^{es ein Drehfeld.}

Weil h solchen

Bedingungen

unterworfen

ist,

^{ersetzen wir h}

durch v,

wobei v⁼1

+

³

(n

^—

1)

^{für n=}

1, 3, 5,

^{7••• oo}

v⁼5

+

³

(n —2)

^{für n=}

2, 4, 6,

^{8-•• oo}

h stellt somit nur eine

beliebige ungerade

^Zahl

dar,

^v

dagegen

^muß

die

obigen Gleichungen

^{erfüllen. -}

Das resultierende Drehfeld kann somit in

folgender

Art ge¬

schrieben werden:

4

smVlT3

/ \

»4y==(_l)n-i_ BJ ^cos ß, t

+ ^(— l)n

^{v« .}

7iV y £ \ I

smv g

Dieses Drehfeld der v-fachen

Polpaarzahl

^{rotiert mit einer}

Winkelgeschwindigkeit

^{—- und an der Stelle a}

pulsiert

^{es mit der}

Kreisfrequenz wl-\-(

^—

l)n

^—

(v

^a).

Zur

Bestimmung

^der Drehinduktivität

IA

bilden wir zuerst die resultierende

Flußverkettung !Pjk

^{für eine}

Spulengruppe

^{der Phase}

k,

welche der vten Harmonischen des Statordrehfeldes

entspricht

^=iaL;k ⁺ ibL;k + ici4.

Hierin kann k⁼ a, b oder ^c

sein, wobei ia

⁼

Ja

^sin

œ,1, ib

⁼

^Jb

^{sin (}o\ t ^s-

ic

⁼

Jc

^sin

Iw11

^{— 2•}

-~-l

Ja

^=Jb⁼⁼Je ⁼⁼«•

Bei

der'gewählten Lage

^des

Koordinatenanfanges

^{ista=konst=0.}

Setzen wir daher die Werte von S. 28 von

L*k, L^k

^und

L^t

in die

obige Gleichung ein,

^{so erhält man:}

!Pjk

⁼

^(-l)»

⁺ⁱ

JL; \

^cos

(œtt ^{+ (-1)"} (v| ^{+ (k-a)} Y~fj.

Der Ausdruck

/

sin v -s-

\

^«

TV3

„8/ ^{21. v* 3} TV

Lm ₂ ^{--= *B}

^vm —r 'sm^"?1

^{" = '}

\sin

^v

^T

stellt die Drehinduktivität dar.

Da

jetzt

^die Induktivitäten des Stators bekarint

sind,

^können wir zur

Ermittlung

^{der EMkten im} Stator schreiten.

Die induzierte EMK in einer

Spule

^{k des Stators}kann entweder aus der Formel

;.=a

oder aus der Formel @⁼

[v 33]

^{bestimmt werden.}

Aus der ersten Formel

ergibt

^sich:

pv sk

-

*^— dt

~

-1)»+»

^J

VA

co,

sin^

^t

^{+ (-l)n (v| + (k-a)}

^v

^)|

Wir kommen zum

gleichen Resultat,

^{wenn wir die induzierte}

EMK aus der Formel

@

⁼

[o 33]

^ableiten.

Indiesem Falle wird für

g1-Stäbe

^{an der Stelle a} die induzierte EMK

e^a

ⁱⁿ

folgender

^Art

ausgedrückt:

e„a

=

vB/ivQ1,

^{wobei v die}

relative

Geschwindigkeit

^{bedeutet. Die}

Ankerlänge

^{ist = 1.}

Für v hat man den Ausdruck:

, , -, d

\

^{1 Ttr}

co.114- ^—l)a-T7^{va —r, —=t.}

'dt

lp-v

^' p