Mean-Field-Theorie für den Ferromagneten

(1)

Mean-Field-Theorie für den Ferromagneten

Sebastian Lüker 1. Dezember 2009

Inhaltsverzeichnis

1 Paramagnetismus 2

2 Ferromagnetismus 4

3 Berechnung der kritischen Exponenten 6

3.1 Kritischer Exponent des Ordnungsparameters . . . . 6

3.2 Kritischer Exponent der kritischen Isotherme . . . . 7

3.3 Kritische Exponenten der Suszeptibilität . . . . 7

3.4 Kritische Exponenten der Wärmekapazität . . . . 8

3.5 Zusammenfassung der kritischen Exponenten . . . . 8

(2)

1 Paramagnetismus

Als Paramagnetismus bezeichnet man die Reaktion von magnetischen Momenten auf ein äuÿeres Magnetfeld B ~ . Das magnetische Moment einer Ladung (z. B.: eines Elektrons) hängt von seinem Drehimpuls ab. Aus diesem Grund wird im folgenden ein Modell angenommen, in dem sich die Spins bzw. Drehimpulse auf den Gitterplätzen eines Festkörpers benden. Für die Herkunft der Drehimpulse sind z. B. ungefüllte Elektronenschalen ver- antwortlich, wie etwa die 3d-Schale der Übergangsmetalle, die 4f-Schale der Seltene Erden oder die 5f-Schale der Actinide.

Als Ausgangspunkt für alle weiteren Berechnungen wird das Heisenberg-Modell benutzt:

H = − X

i,j

J

_ij

J ~

_i

J ~

_j

− gµ

_B

X

i

J ~

_i

B ~ (1)

Hier bezeichnet J

_ij

die Austauschintegrale mit J

_ij

= J

_ji

und J

_ii

= 0 , J ~

_i

einen Drehimpuls J am Gitterplatz i, B ~ das äuÿere Magnetfeld, µ

_B

das Bohrsche Magneton und g den gyromagnetischen Faktor.

Für den Paramagnet wird angenommen, dass die Spins nicht miteinander Wechselwirken, sodass sich der Hamiltonoperator (1) vereinfacht zu:

H

0

= −gµ

_B

X

i

J ~

_i

B ~ B ~ = B · ~ e

_z

(2) Da für einen Spin im Magnetfeld J ~

_i

· B ~ = m

_i

B mit m

_i

= −J, −J + 1, ..., J gilt, vereinfacht sich dieser Hamitonoperator zu:

H

0

= −gµ

_B

X

i

m

_i

B (3)

Daraus lässt sich mit x = gµ

B

βB und β =

_kT¹

die kanonische Zustandssumme berechnen Z:

Z =

J

X

m1=−J

· · ·

J

X

mN=−J

exp(x

N

X

i=1

m

_i

) =

"

_J

X

m=−J

e

^xm

#

N

=

e

^{J x}

+ e

^(J−1)x

+ ... + e

^{−J x}

N

=

e

^{J x}

(1 + e

^−x

+ ... + e

^{−2J x}

)

N

· e

¹²^x

e

¹²^x

!

N

· 1 − e

^−x

1 − e

^−x

N

=

"

e

^(J+¹²^)x

e

¹²^x

· 1 − e

^−(2J+1)x

1 − e

^−x

#

N

=

"

e

^(J+¹²^)x

− e

^−(J+¹²^)x

e

¹²^x

− e

⁻¹²^x

#

N

=

sinh[(J +

¹₂

)x]

sinh[

¹₂

x]

^N

⇒ Z =

sinh[(J +

¹₂

)x]

sinh[

¹₂

x]

^N

Insbesondere gilt für J =

¹₂

: Z

_J=¹

2

=

sinh(x) sinh(

¹₂

x)

N

=

2 sinh(

¹₂

x) cosh(

¹₂

x) sinh(

¹₂

x)

^N

= 2

^N

· cosh

^N

( 1

2 x) (4)

(3)

Aus der kanonischen Zustandssumme lässt sich die freie Energie F berechnen:

F = −kT ln(Z) = −N kT ln

sinh[(J +

¹₂

)x]

sinh[

¹₂

x]

(5) Über die freie Energie lässt sich die Magnetisierung M = −

^∂F_∂B

T

berechnen:

M = M

₀

2J + 1 2J coth

2J + 1 2J J x

− 1 2J coth

1 2J J x

≡ M

₀

· B

_J

(J βµ

_B

gB) (6) Hier bezeichnet M

₀

= N J gµ

_B

die Sättigungsmagnetisierung und B

_J

(J βµ

_B

gB) die Brillouin-Funktion:

B

_J

(x) = 2J + 1 2J coth

2J + 1 2J x

− 1 2J coth

1 2J x

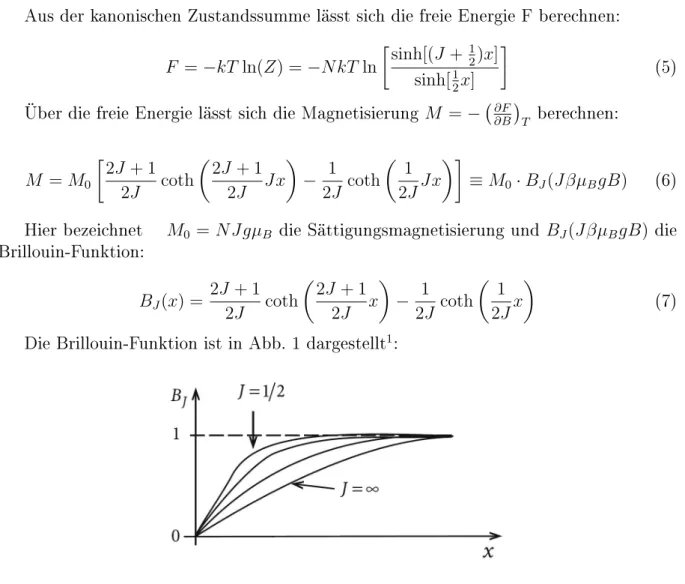
(7) Die Brillouin-Funktion ist in Abb. 1 dargestellt

¹

:

Abbildung 1: Die Brillouin-Funktion für verschiedene Werte von J

Für x → 0 gilt B

_J

(x) → 0 und somit M → 0 , der Paramagnet besitzt somit keine spontane Magnetisierung.

Für J → ∞ gilt B

∞

(x) = coth(x) −

_x¹

, dies ist die Langevin-Funktion, die schon in der klassischen Thermodynamik zur Beschreibung von magnetischen Phänomenen benutzt wird.

Die Brillouin-Funktion ist ungerade, das heiÿt es gilt B

_J

(x) = −B

_J

(−x) . Dies bedeutet, dass das Umpolen des äuÿeren Magnetfeldes auch die Magnetisierung umpolt.

Es gilt B

_J

(x)

^x→∞

−→ 1 . Dies bedeutet, dass die Magnetisierung für groÿe Magnetfelder gegen die Sättigungsmagnetisierung konvergiert.

Für kleine Argumente lässt sich die Brillouin-Funktion als Reihe entwickeln:

B

_J

(y) = J + 1

3J y − J + 1 3J

2J

²

+ 2J + 1

30J

²

y

³

+ O (y

⁵

) (8) Somit gilt für die Magnetiseirung M bei hohen Temperaturen ( βµ

_B

gB =

^µ^B_kT^gB

<< 1 ):

M (T, B) ≈ C

T B → Curie-Gesetz (9)

Dies ist das Curie-Gesetz mit der Curie-Konstante C =

^J(J+1)_3k

N (gµ

_B

)

²

.

1

Quelle: Nolting, Grundkurs theoretische Physik 6, 6. Au., p. 330

(4)

2 Ferromagnetismus

Im folgenden wird die Wechselwirkung zwischen den einzelnen Spins berücksichtigt. Des- halb muss der gesamte Hamitonoperator betrachtet werden:

H = − X

i,j

J

_ij

J ~

_i

J ~

_j

− gµ

_B

X

i

J ~

_i

B ~ ≡ H

₁

+ H

₀

(10) Zur Auswertung des Hamiltonoperators folgen wir der Weiss'schen Theorie des Fer- romagnetismus. In dieser Theorie wird die Mean-Field-Näherung bzw. die Molekularfeld- Näherung durchgeführt. Die Idee hinter dieser Näherung ist, dass die Spin-Spin-Wechselwirkung durch ein mittleres Magnetfeld ersetzt werden soll. Die Spins werden somit voneinander entkoppelt und wechselwirken nur noch mit dem mittleren Feld.

Zunächst wird der Wechselwirkungsterm umgeformt:

H

₁

= − X

i,j

J

_ij

J ~

_i

J ~

_j

= − X

i,j

J

_ij

(J

_i^x

J

_j^x

+ J

_i^y

J

_j^y

+ J

_i^z

J

_j^z

) = − X

i,j

J

_ij

(J

_i⁺

J

_j⁻

+ J

_i^z

J

_j^z

) (11) Hier wurden die Auf- und Absteigeoperatoren J

^±

= J

^x

± iJ

^y

benutzt.

Für die Mean-Field-Näherung erweist sich folgende Operator-Identität als Zweckmä- ÿig:

A · B = (A− < A >)(B− < B >)

| {z }

F luktuationen

+A < B > +B < A > − < A >< B >

| {z }

Konstante: c˜

(12)

Damit ergibt sich für den Wechselwirkungsanteil des Hamiltonoperators:

H

₁

= − X

i,j

J

_ij

J ~

_i

J ~

_j

= − X

i,j

J

_ij

(J

_i⁺

J

_j⁻

+J

_i^z

J

_j^z

) ≈ − X

i,j

J

_ij

(J

_i^z

< J

_j^z

> + < J

_i^z

> J

_j^z

) (13) Im letzten Schritt wurde die Mean-Field-Näherung durchgeführt:

1. Die Fluktuationen werden vernachlässigt

2. Wegen der Drehimpulserhaltung: < J

_i⁺

>=< J

_i⁻

>= 0 folgt J

_i⁺

J

_j⁻

→ 0

3. Die Konstante ˜ c wird vernachlässigt, da sie nur einen konstanten Beitrag zur Energie liefert

Bei genauerer Betrachtung des Wechselwirkungsanteils zeigt sich, dass die Spin-Spin- Wechselwirkung durch ein mittleres Feld B

_{M F}

ersetzt wurde:

H

_{M F}

= (−2J

₀

< J

^z

> −gµ

_B

B)

N

X

i=1

J

_i^z

≡ −gµ

_B

B

_{M F}

N

X

i=1

J

_i^z

(14) Hier wurde J

₀

≡ P

i

J

_ij

= P

j

J

_ij

benutzt.

B

M F

= B +

^2J⁰_gµ^<J^z^>

B

≡ B + B

ex

bezeichnet das mittlere Feld, und B

ex

das Austauschfeld, das die Wechselwirkung der Spins untereinander ersetzt.

Das Austauschfeld ist proportional zur Magnetisierung, es gilt:

2J 2J

(5)

Mit diesem Feld ist die Berechnung der Magnetisierung analog zum Paramagneten, wenn man B → B

_{M F}

ersetzt. Damit ergibt sich für die Magnetisierung:

⇒ M = M

₀

B

_J

[βgµ

_B

J(B + λM )] (17) Im Nullfeld (B=0) gilt:

M = M

₀

B

_J

(βgµ

_B

J λM ) (18)

Dies ist eine implizite Gleichung zur Bestimmung der spontanen Magnetisierung M

_S

. Oensichtlich existiert immer eine Lösung für M = 0 , was bedeutet, dass keine spontane Magnetisierung vorliegt. Um weitere Lösungen zu nden, wurde die linke Seite von (18) gegen die rechte Seite aufgetragen

²

:

Man erkennt, dass zwei weitere Lösungen der Gleichung existieren, wenn die Stei- gung der Brillouin-Funktion im Ursprung gröÿer als die Steigung der Geraden ist. Zur Berechnung der Steigung der Brillouin-Funktion bietet sich somit die Reihenentwicklung an:

d dM

S

[M

₀

B

_J

(βgµ

_B

J λM

_S

)] ≈ d dM

S

M

₀

J + 1 3J

gµ

_B

J λ kT M

_S

= C λ

T (19)

Hier bezeichnet C =

^J^(J_3k⁺¹⁾

N (gµ

_B

)

²

die Curie-Konstante. Für

^Cλ_T

> 1 existieren zwei weitere Lösungen.

Über diese Ungleichung deniert sich die Curie-Temperatur zu T

_C

= Cλ . Bei T = T

_C

n- det ein Phasenübergang statt. Unterhalb der Curie-Temperatur besitzt das System eine spontane Magnetisierung M

_S

, oberhalb von T

_C

verschwindet diese Magnetisierung. Die spontane Magnetisierung eignet sich daher als Ordnungsparameter. Für eine verschwin- dene Spin-Spin-Wechselwirkung λ → 0 geht T

_C

→ 0 , das System verhält sich in diesem Grenzfall erwartungsgemäÿ paramagnetisch. Es fällt auf, dass die Curie-Temperatur nicht von der Gitterdimension abhängt. Dies ist ein Widerspruch zum Experiment, wo eine sol- che Abhängigkeit gemessen wird.

2

Quelle: Nolting, Grundkurs theoretische Physik 6, 6. Au., p. 334

(6)

3 Berechnung der kritischen Exponenten

Im folgenden werden die kritischen Exponenten des Ferromagneten in der Mean-Field- Näherung berechnet. Zur Vereinfachung der Rechnung wird im folgenden J =

¹₂

angenommen, die kritischen Exponenten sind aber für alle J dieselben. Für die Magnetisierung ergibt sich für J =

¹₂

:

⇒ M = M

0

tanh 1

2 βgµ

B

(B + λM )

(20) Um die folgenden Berechnungen übersichtlicher zu gestalten werden die reduzierten Variablen σ =

_M^M

0

und T e =

_T^T

C

deniert. Damit wird (20) zu:

⇒ σ = tanh 1

2 gµ

B

kT + σ T e

(21) Für die Berechnung der kritischen Exponenten ist es zweckmäÿig, die Hilfsfunktion h einzuführen:

h ≡ tanh

gµ

_B

B 2kT

= σ − tanh(

^σ

Te

) 1 − σ tanh(

^σ

Te

) (22)

Man überzeugt sich leicht von der Gültigkeit dieser Funktion mit folgender trigono- metrischen Identität:

tanh(x + y) = tanh(x) + tanh(y)

1 + tanh(x) tanh(y) (23)

In der Nähe des kritischen Punktes (B=0, M=0, T = T

_C

) lässt sich die Hilfsfunktion entwickeln:

h = σ

1 − 1 T e

+ σ

³

1 3f T

³

+

1 − 1

T e 1

T e

+ O (σ

⁵

) (24) Hier wurde die Entwicklung des Tangens-Hyperbolicus benutzt:

mit tanh(x) = x − 1

3 x

³

+ 2

15 x

⁵

+ O (x

⁷

) (25)

3.1 Kritischer Exponent des Ordnungsparameters

Der kritische Exponent der Ordnungsparameters ist deniert durch:

M

S

∝ (−)

^β

für B = 0, T → T

C

T < T

C

, = T − T

_C

T

_C

(26)

Für B=0 ergibt sich für die Hilfsfunktion:

h = tanh

gµ

_B

B 2kT

= 0 (27)

Damit folgt aus (24):

σ

²

=

TC

T

− 1

T_C³

3T³

+

^T_T^C

(1 −

^T_T^C

)

+ ... ≈ 3 T

T

_C

2

T

C

− T

T

_C

(28)

(7)

3.2 Kritischer Exponent der kritischen Isotherme

Der kritische Exponent der kritischen Isotherme ist deniert durch:

B ∝ M

^δ

für T = T

C

, T e = 1 (30) Für T e = 1 gilt

h = tanh

gµ

_B

B 2kT

= σ

1 − 1 T e

| {z }

=0

+σ

³





 1 3f T

³

+

1 − 1 T e

| {z }

=0

1 T e







+ ... (31) Damit ergibt sich der Zusammenhang zwischen dem Magnetfeld B und der Magneti- sierung M zu:

⇒ gµ

B

2kT B + O (B

³

) = σ

³

3 + O (σ

⁵

) mit σ ∝ M (32) Hieraus folgt der kritische Exponent der kritischen Isotherme zu:

δ = 3 (33)

3.3 Kritische Exponenten der Suszeptibilität

Die kritischen Exponenten der Suszeptibilität sind deniert durch:

χ

_T

∝ (−)

^−γ⁰

für T → T

_C

, T < T

_C

, B = 0, = T − T

_C

T

_C

(34)

χ

T

∝

^−γ

für T → T

C

, T > T

C

, B = 0, = T − T

_C

T

_C

(35)

Für die Suszeptibilität gilt:

χ

_T

= ∂M

∂B

T

= ∂M

∂σ

T

∂σ

∂h

T

∂h

∂B

T

(36)

= 1

2 N gµ

_B

∂σ

∂h

T

1 2 βgµ

_B

= C T

∂σ

∂h

T

(37) Die Ableitung

^∂σ_∂h

T

lässt sich mit der Hilsfunktion berechnen:

h = σ

1 − 1 T e

+ σ

³

1 3 T f

³

+

1 − 1 T e

1 T e

+ O (σ

⁵

) Dierentiation auf beiden Seiten ergibt:

1 = ∂σ

∂h

1 − 1 T e

+ 3σ

²

1 3 T e

³

+ O (σ

⁴

)

(38) Damit ergibt sich für die Suszeptibilität:

⇒ χ

_T

= C T

T e + σ

²

T e

³

+ O (σ

⁴

)

−1

(39) Für T < T

C

gilt σ

²

≈ −3 . Damit ergibt sich:

⇒ χ

_T

≈ 1 2

C

T (−)

⁻¹

⇒ γ

⁰

= 1 (40)

(8)

Für T > T

_C

und B=0 gilt σ = 0 . Damit ergibt sich das Curie-Weiss-Gesetz:

⇒ χ

_T

= C T

T

_C

T

T − T

_C

T

_C

−1

= C

T − T

_C

= C

T

_C

⁻¹

(41)

Damit ergeben sich die kritischen Exponenten der Suszeptibilität zu:

γ

⁰

= 1 für T < T

_C

(42)

γ = 1 für T > T

_C

(43)

3.4 Kritische Exponenten der Wärmekapazität

Die kritischen Exponenten der Wärmekapazität sind deniert durch:

C

H

∝ (−)

^−α⁰

für T → T

C

, T < T

C

, B = 0, = T − T

_C

T

_C

(44)

C

_H

∝

^−α

für T → T

_C

, T > T

_C

, B = 0, = T − T

_C

T

_C

(45)

Für die Wärmekapazität C

_H

gilt:

C

_H

= T χ

⁻¹_T

∂M

∂T

H

2

(46) Da für T > T

_C

die spontane Magnetisierung M

_S

= 0 ist, folgt sofort C

_H

= 0 und damit α = 0 .

Für T < T

_C

ergibt sich mit C

_H

= −T

∂²F

∂T²

H

durch eine elementare aber lange Rechnung:

C

_H

= 3 2 N k

1 − O

T

_C

− T T

_C

(47) Damit ergeben sich die kritischen Exponenten der Wärmekapazität zu:

α

⁰

= 0 für T < T

_C

(48)

α = 0 für T > T

C

(49)

Oensichtlich ist die Wärmekapazität unstetig beim Phasenübergang, sie macht einen Sprung um ∆C

_H

=

³₂

N k für J =

¹₂

.

3.5 Zusammenfassung der kritischen Exponenten

Die kritischen Exponenten des Ferromagneten in der Mean-Field-Näherung:

Kritischer Exponent Wärmekapazität C

H

α = α

⁰

= 0 Ordnungsparameter M

_S

β =

¹₂

Suszeptibilität χ

_T

γ = γ

⁰

= 1

Kritische Isotherme B δ = 3

Die kritischen Exponenten sind identisch mit den kritischen Exponenten des Van der Waals-Gases und der Landau-Theorie. Diese drei Theorien werden auch als klassische Theorien bezeichnet, sie sind äquivalent.

Wie beim Van der Waals-Gas lässt sich auch für den Ferromagneten zeigen, dass die