Wie Geometrie zu einem anwendungsbezogenen und alltagsrelevanten Mathematikunterricht beitragen kann
Volltext
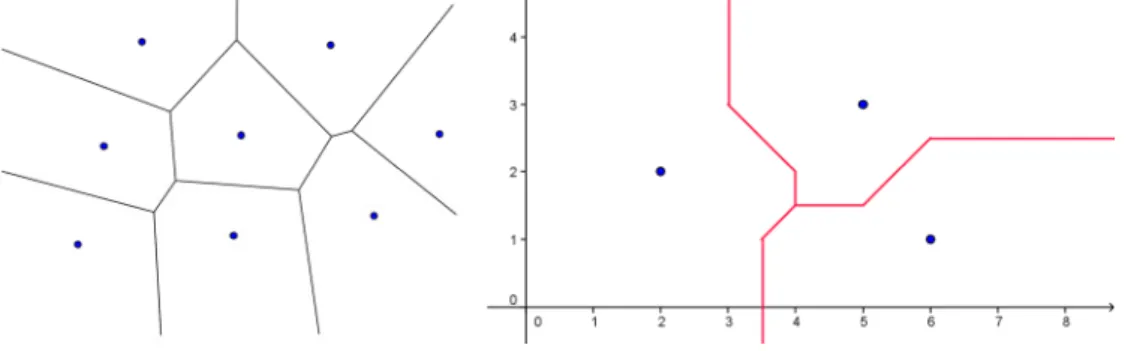
Abbildung
ÄHNLICHE DOKUMENTE
(meist uneingestandene) Risikoscheu mancher Kollegen wird verständlich, wenn man bedenkt, daß die Hochschule das schulübliche bloße Reagieren auf vorgelegte Aufgaben
• für das Lösen mathematischer Probleme geeignete Darstellungen auswählen und nutzen. Nutzung mathematischer Hilfsmittel
Diese und weitere Verstehenselemente müssen Schülerinnen und Schüler in einem kognitiven Aufbauprozess geeignet miteinander verknüpfen, da- mit sie den Satz des
In diesem Zusammenhang ist bisher wenig untersucht, wie sich der aus ma- thematik-didaktischer Sicht wichtige Einsatz graphischer Repräsentationen tatsächlich im Unterricht
Hält sich zu diesem Zeitpunkt die Lehrperson mit ihren regulä- ren Vorstellungen zurück, kann sie durch geeignete Fragen die Reflexion über die singulären
auch aus dem Fach Mathematik selbst heraus definieren muss, stellt sich die Frage, inwiefern sich eine Beschreibung schöner Mathematik auf etwaige Schön- heit von
Vielmehr geht es um eine Urteilskraft gegenüber Algorithmen in unserer Welt: „I refer to be- ing aware of the presence of algorithms in their lives, and the increasing role they
Um zunächst Einblicke zu erhalten, wie viele Zeichnungen von Ler- nenden selbst angefertigt werden, wurde mittels einer Pilotstudie eine Be- standsaufnahme erstellt, wie