1 9 1 1 1 0 1 [ill 1 1 2 1
[I31 [I41
1 1 5 1 1 1 6 1
MA: MIT, 1963.
P. R. Chevillat, “Fast sequential decoding a n d a new complete [17]
decoding algorithm,” Ph.D. dissertation, Dept. Elec. Eng., Illinois [18]
Institute of Technology, Chicago, IL, May 1976.
K. Zigangirov, “Some sequential decoding procedures,” ProbZemy Peredachi Znformatsii, vol. 2, pp. 13-25, 1966. 1 1 9 1
F. Jelinek, “A fast sequential decoding algorithm using a stack,”
IBM J. of Res. a n d Dev., vol. 13, pp. 675-685, NOV. 1969.
J. Geist, “Algorithmic aspects of sequential decoding,” Ph.D. dis- [20]
sertation, Dept. Elec. Eng., Univ. Notre Dame, Notre Dame, IN, Aug. 1970.
W. W. Peterson a n d E. J. Weldon, Error-Correcting Codes, 2 n d Ed. [21]
Cambridge, MA: MIT, 1972.
P. R. Chevillat a n d D. J. Costello, “Distance a n d computation in sequential decoding,” IEEE Trans. Commun., vol. COM-24, pp. [22]
440-447, Apr. 1976.
R. Johannesson, “Robustly optimal rate one-half binary convolu- tional codes,” IEEE Trans. Inform. Theory, vol. IT-21, pp. [23]
464-468, July 1975.
D. J. Costello, “Free distance bounds for convolutional codes,”
IEEE Trans. Znform. Theory, vol. IT-20, pp. 356-365, May 1974.
J. M. Wozencraft, Private Communication. Oct. 1974.
J. L. Massey a n d D. J. Costello, “Nonsystematic convolutional codes for sequential decoding in space applications,” IEEE Trans.
Commun. Tech., vol. COM-19, pp. 806-813, Oct. 1971.
L. R. Bahl a n d F. Jelinek, “Rate l/2 convolutional codes with complementary generators,” IEEE Trans. Znform. Theory, vol.
IT-17, pp. 718-727, Nov. 1971.
K. J. Larsen, “Short convolutional codes with maximal free dis- tance for rates l/2, l/3, a n d l/4,” IEEE Trans. Inform. Theoy, vol. IT-19, pp. 371-372, May 1973.
E. Paaske, “Short binary convolutional codes with maximal free distance for rates 2/3 a n d 3/4,” IEEE Trans. Inform. Theory, vol.
IT-20, pp. 683-689, Sept. 1974.
D. Haccoun a n d M. J. Ferguson, “Generalized stack algorithms for decoding convolutional codes,” IEEE Trans. Inform. Theory, vol. IT-21, pp. 638-651, Nov. 1975.
R. Johannesson, “O n the computational problem with sequential decoding,” presented at the IEEE International Sym. o n Inform.
Theory, Ronneby, Sweden, June 21-24, 1976.
The Gaussian W ire-Tap Channel
s. K. LEUNG-YAN-CHEONG, MEMBER, IEEE, AND MARTIN E. HELLMAN, MEMBER, IEEE
Abstract-Wyner’s results for discrete memoryless wire-tap channels are extended to the Gaussian wire-tap channel. It is shown that the secrecy capacity C, is the difference between tbe capacities of the main a n d wire-tap channels. It is further shown tbat Rd= C, is the upper boundary of the achievable rate-equivocation region.
I. INTRODUCTION
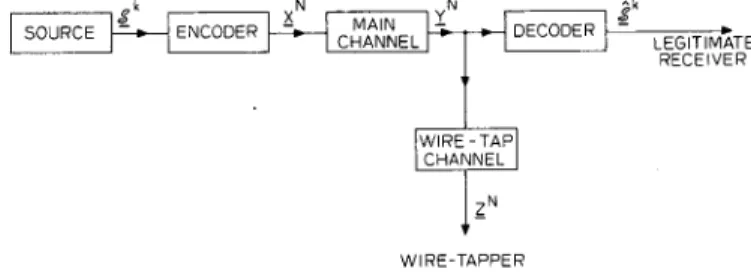
1 N A RECENT insightful paper [l] Wyner introduced 1 the wire-tap channel shown in F ig. 1. It is a form of degraded broadcast channel [2], with the novel difference that o n e information rate is to b e maximized a n d the other m inimized. T h e object is to maximize the rate of reliable communication from the source to the legitimate receiver, subject to the constraint that the wire-tapper learns as little as possible about the source output. T h e wire-tapper knows the encoding scheme used at the trans- m itter a n d the decoding scheme used by the legitimate receiver, a n d is kept ignorant solely by the greater noise
Manuscript received June 4, 1976; revised November 9, 1977. This
work was supported in part by the National Science Foundation under Grant ENG-10173. in Dart bv the United States Air Force Office of Scientific Research under Contract F44620-73-C-0065, a n d in part by the Joint Service Electronics Program under Contract NOC014- 75-c-0601.
S. K. Leung-Yan-Cheong was with the Department of Electrical Engineering, Stanford, CA. He is now with the Department of Electrical Engineering, Massachusetts Institute of Technology, Cambridge, MA.
M. E. Hellman is with the Department of Electrical Engineering, Stanford University, Stanford, CA. -
S O U R C E E N C O D E R D E C O D E R 1 ” .
LEGITIMATE RECEIVER
WIRE-TAPPER
Fig. 1. General wire-tap channel.
present in his received signal. Thus while the objective is the s a m e as in cryptography, the technique used to achieve privacy is very different.
T h e source is stationary a n d ergodic, a n d has a finite alphabet. T h e first k source outputs tik are encoded into a n N-vector xN which is input to the m a in channel. T h e legitimate receiver makes a n estimate ^,” of 9 based o n the output yN of the m a in channel, incurring a block error rate
P,=Pr(hk#Zk). (1)
yN is also the input to the wire-tap channel a n d the wire-tapper has a n average residual uncertainty H(Sk IZN) after observing the output z N of the wire-tap channel. O f course it does not change the problem if z N is the output of a single channel with input x N, which is statistically equivalent to the cascade of the m a in a n d wire-tap chan- nels, since dependencies between z N a n d y N are im- 001%9448/78/0700-451$00.75 0 1 9 7 8 IEEE
452 IEEE TRANSACTIONS O N INF’ORMATION THEORY, VOL. IT-M, NO. 4, JULY 1978
material. We define the fractional equivocation of the wire-tapper to be
A=H(SkIZN)/H(Sk) (2)
and the rate of transmission to be
R = H(Sk)/N. (3)
We shall say that the pair (R*,d*) is achievable if for all e > 0 there exists an encoder-decoder pair such that
R>R*-e, Ah)*-e, and P,<e. (4) Our definitions are slightly different from Wyner’s origi- nal definitions. For example, Wyner defines A = m Wk. w e will drop superscripts when the context permits.) The new definitions have the advantage that the achievable (R, d) region depends only on the channels and not on the source.
Wyner has determined the achievable (R, d) region when both channels are discrete memoryless channels. He shows that in most cases there is a secrecy capacity C, > 0 such that (R,d)=(C,, 1) is achievable. By operating at rates below C,, it is possible to ensure that the wire-tapper is essentially no better informed about a after observing z than he was before.
A particularly simple example results when both the main and wire-tap channels are binary symmetric chan- nels (BSC) with crossover probabilities of 0 andp respec- tively, and the source is binary symmetric. (Then H @ ‘)=
k, and our definition is equivalent to Wyner’s.) Wyner shows that
R<l (5)
d<l (6)
Rd(h(p) (7)
defines the set of achievable points. As noted by Wyner, this region is not convex. Surprisingly, however, Rd= c as in (7) corresponds to a time-sharing curve as established in the following lemma.
Lemma I: Let R,d, = R,d,= c, a constant. Assume R,
>R, and hence d,<d,. If the points (R,,d,) and (R,,d&
are achievable, then by time-sharing any point (R,d) with R2 < R < R,, d, < d 6 d,, and Rd = c is achievable.
Proof: Consider a block of N channel uses. Assume that for cwN transmissions we operate at (R,,d,) and for (1 - cr)N transmissions we operate at (R,,d&. Then the effective equivocation is
d aNR,d, + (1 - a)NR,d,
= aNR,+(I-a)NR, ’ (8)
The effective transmission rate is
R=[aNR,+(l-a)NR,]/N (9)
so that
Rd=aR,d,+(l-a)R2d2. (10)
We see that time-sharing averages the product R&, so if
R,d, = Rzdz = c, then Rd = c. Q.E.D.
This lemma will be of importance in establishing the achievable (R,d) region for the Gaussian wire-tap chan-
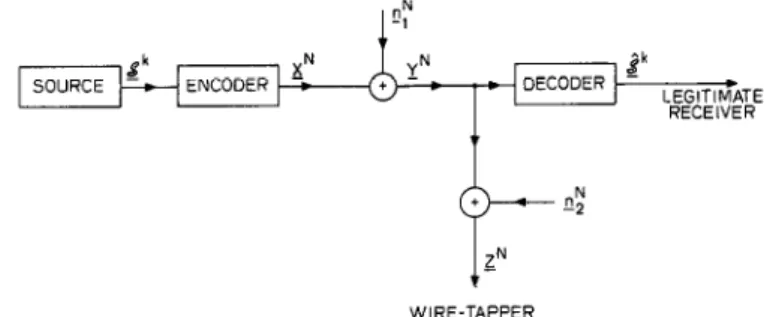
S O U R C E E N C O D E R D E C O D E R Jk - .
LEGITIMATE R E C E I V E R
r + N
“2
ZN WIRE-TAPPER
Fig. 2. Gaussian wire-tap channel.
nel, shown in Fig. 2. As before the source is a stationary ergodic finite alphabet source. The noise vectors $ and II” are independent and have components that are i.i.d.
%(O,a:) and GJ(O,u$), respectively. The channel is power lim ited in that
(11)
In the following two sections we utilize Wyner’s framework to completely characterize the achievable (R,d) region for this Gaussian wire-tap channel. Letting
cM=1/210g(1+P/a:) (12)
and
C M W = l/2 log (1 + P/( uf + 0;)) (13)
denote the capacities of the main and overall wire-tap channels, respectively, we shall show that the secrecy capacity is given by
cs=&f-&/ (14
and that in general we have the following result.
Theorem I: For the Gaussian wire-tap channel, the set 3, of all achievable (R,d) pairs is defined by
R<C, (15)
d<l (16)
Rd < C,. (17)
In the next section, we establish the achievability of this region by showing that the extreme points of 3,
UW4)=G.&/Cd (18)
and
(&d,)=WsJ) (19)
are both achievable. We then invoke the tim e sharing argument, and say that since R,d, = Rzdz= C, the entire region ‘3, defined in Theorem 1 is achievable.
In Section III we establish the converse, that any point outside 3, is not achievable.
II. DIRECT HALF OF THEOREM 1
As noted above we need only establish that the two points (R,,d,) and (R,,d,) defined by (18) and (19) are achievable, since time-sharing then implies the achievabil- ity of the entire region $Il of Theorem 1.
T h e point (R,,d,) is trivially achieved by coding as if the wire-tapper was absent. Usual source a n d channel coding arguments show that it is possible for R to b e arbitrarily close to C M = R, a n d P, to b e arbitrarily close to 0. But the information gained by the wire-tapper is lim ited by the capacity of his channel so that
A=H(SkIZN)/H(S~))(H(Sk)-NC~W)/H(S’)
=I-(C&R). (20) As R approaches CM, this lower b o u n d o n A approaches CJ CM= d,. Thus the point (R,,d,) is achievable.
W e will establish the achievability of (R,,d& =(C,, 1) by proving a somewhat stronger result, similar to that of Hellman a n d Carleial [3]. If C, = CM/2, T h e o r e m 1 states that, by cutting our rate in half, we can completely foil the wire-tapper. Instead, we will show that it is possible to send two independent messages reliably, each at a rate near C, = CM/2, a n d each totally protected from the wire-tapper o n a n individual basis. T h e penalty is that, if the wire-tapper learns o n e message through other means, h e can then also determine the other message. In general, if C, > CM/L, we will show that L independent messages can b e simultaneously a n d reliably communicated to the legitimate receiver, each at a rate near CM/L, a n d each totally protected o n a n individual basis. However, if the wire-tapper learns any o n e message, h e m a y b e able to determine all of the others. By using random noise for all but the first message, we can obtain the direct half of T h e o r e m 1 as a special case of T h e o r e m 2.
T h e o r e m 2: Let urn b e a sequence of m outputs from a finite-alphabet stationary ergodic source with per letter entropy H(Q), a n d let aP b e any p consecutive compo- nents of urn. T h e n provided
it is cate uses
R,=H(%f”)/N< C M (21)
Rs=H(sP)/N< C,, (22)
possible, by choosing N large enough, to communi- urn to the legitimate receiver reliably in N channel a n d yet to ensure that
As=H(t$IZN)/H(bP) (23)
is arbitrarily close to 1.
Further, if { af }f-, are L such consecutive p-tuples of urn, it is possible to ensure that
A,i~H(~lZN)/H(SP) (24)
is arbitrarily close to 1 for 1 <i < L, with L fixed as N+CQ.
Remarks:
1) An alternative notation would b e to use s”’ in place of am, but then superscripts would b e necessary to dis- tinguish between the entire ergodic source output a n d its projection, Sp, to b e kept secret. It is h o p e d that this remark will remove any confusion caused by our choice of notation.
2) Until now, the entire sequence urn was to b e pro- tected so that m =p, R, = R,, a n d As = Ar. Now the distinc-
tion between urn a n d its projection sp requires us to distinguish between the total rate RI a n d the secrecy rate 4
3) For memoryless sources thep outputs in Sp n e e d not b e consecutive, a n d more general p-dimensional projec- tions are possible. See [3] for a generalization to linear projections.
T h e o r e m 2 will b e established by proving a sequence of lemmas. F irst, since the source is ergodic, we have:
L e m m a 2: It is possible to source code n ”’ into a binary n-vector u ” such that each of the $ ’ are determined reliably (i.e., as N-co the probability of error tends to 0) by k consecutive components s/‘ of u ” a n d
n=N(C,-29 (25)
k=N(C,-c) (26)
with e > 0.
Remarks: urn denotes the entire ergodic source output, a n d sp denotes a p-dimensional projection thereof; u ” denotes the binary source-coded version of urn, a n d sk denotes a k-dimensional projection thereof. Further sk is a binary source-coded version of a ’.
Proof From (21) a n d (22), we can define
e=min {(CM- R,)/3,(C,- R,)/2} >O. (27) In proving that R, a n d RI can b e m a d e to approach C, a n d CM, while As is kept arbitrarily close to 1, we can redefine R, a n d R, so that
(CM-R,)/3=(C,-R,)/2=r (28)
where e is given by (27) since excess rate can b e discarded.
T h e noiseless source coding theorem for ergodic sources [4, theorem 3.5.31 then implies that (25) a n d (26) can b e satisfied. There is a m inor problem in ensuring that sk consists of k consecutive bits of u ”, but this is easily overcome.
If, the { tir } are disjoint, we clearly can code in sub- blocks while satisfying (26) a n d the condition that s, b e consecutive bits of u. Even if the {a:} are not disjoint, we can still satisfy these conditions. For example, if ay con- stitutes the first 3/4 of urn a n d 4 constitutes the last 3/4 of urn, we can code u ”’ in four equal subblocks to obtain u ”. T h e union b o u n d guarantees that the overall coding from u to u is reliable since each of the four subcodings is
reliable. Q .E.D.
W e will henceforth deal with only o n e of the si (or bi) that we shall denote as s (or a). W e shall show that, over a suitable ensemble of codes, u can b e communicated reli- ably to the receiver a n d As kept arbitrarily near 1, with probability that approaches 1 as N+w. Use of the union b o u n d then allows us to state that, with probability ap- proaching 1, all L of the A, can b e kept near 1. Now define a n ensemble of channel codes as follows. Each code in the ensemble has 2 ” codewords with blocklength N,
c= {X’,X2; * * ‘X2”}. (2%
454 IEEE TRANSACTIONS O N INFORMATION THEORY, VOL. IT-24, NO. 4, JULY 1978
Each component of each codeword is an i.i.d. random variable with a %(O, P- a) distribution, where (Y >0 is chosen so that
c,(+1/210g(1+(P-a)/a~)>C,-e (30)
and
CM,(+1/210g(1+(P-a)/(a:+a;))>C,,-e.
(31) Since n = N(C, - 2e), the normal coding theorem for Gaussian channels [4, theorem 7.4.21 states that u” is reliably transmitted to the receiver by almost all codes in the ensemble as N+oo. And as N+oc almost all codes in the ensemble satisfy the power constraint (1 l), so almost all codes satisfy both conditions as N-+X.
All that remains is to show that $ A 1 for almost all codes in the ensemble.
Lemma 3:
As>[H(U)TH(UIS,Z)-I(U;Z)]/NCs. (32) Proof: Since s is a deterministic function of ti,
As=H@ W/H(S) (33)
> H(SIZ)/H(S), (34)
and from (22)
H(S) < NC,. (35)
We complete the proof by showing that
H(SfZ)=H(U)-H(UIS,Z)-I(U,Z). (36)
By definition
H(UIZ)=H(U)-I(U;Z) (37)
and, since s is a function of u,
H(UIZ)=H(U,SIZ)=H(SIZ)+H(UIS,Z). (38) Q.E.D.
We now proceed to bound the three terms in (32).
Lemma 4: There exists a sequence of source codes of increasing blocklength such that
H(U)> N&(1-~‘-6) (39 where E’ stands for any term which tends to 0 as e+O, and 6 stands for any term which tends to 0 as N-cc with e > 0 fixed.
Proof From (21) (27), and (28)
H(%)=NR,=N(C,-3c)=NC,(l-c’). (40)
Since u is a deterministic function of u,
H(U)=H(%)-H(‘% IU). (41)
Using the noiseless source coding theorem for ergodic sources [4, theorem 3.5.31 and Fano’s inequality [4, theo- rem 4.3.11, we get
H(%IU)<l+GN, (42)
so that
H(U)>NC,(l-e’)-l-6N=NC,(l-~‘-6). (43) (Note that the two 6’s are not equal.) Q.E.D.
We now bound the second term in (32).
Lemma 5: As N-+cc almost all codes in the ensemble obey
H(UlS,Z)<SN. W)
Proof Since s is a k-dimensional projection of the n-vector u, given s there are only 2”-k =2N(c~w-‘) u’s to be decided among on the basis of z. But the codewords associated with each of these u’s were chosen according to the capacity-achieving distribution, and from (31) we know the error probability given s and z tends to 0 as N+cc for almost all codes. Use of Fano’s inequality completes the proof.
Finally, the data processing theorem and the definition of C,;yield a bound on the third term in (32):
I(U,Z) < NC,,. (45)
Combining (45) and the preceding three lemmas we find that for almost all codes
4>[NC,(l-e’-6)-6N-NC,,]/NC,
=NC,(l-+&)/NC,
= 1 - E’ - 8.
Then letting N+cc with fixed e > 0 we find that lim A,>l-e’
N-CC
and
liio ,lilim A, = 1 for almost all codes.
(46)
(47)
(48) This completes the proof that (R,, d2) = (C,, 1) is achiev- able. An intuitive partial interpretation of the proof is as follows. Suppose the wire-tapper could determine s from z. The residual rate of u is then below the capacity CM, of his channel, and the code is designed so that then the wire-tapper could reliably learn the rest of u. But then the wire-tapper would be gaining information at an overall rate above his channel’s capacity, which is impossible.
Therefore, the initial assumption (that the wire-tapper could determine s) is wrong.
III. CONVERSE THEOREM
In this section we prove the converse part of Theorem 1, that any point (R,d) outside 9. is not achievable. That R < C,,, and d < 1 is self-evident from the definitions. Our real task is to show that
Rd< C, (17)
must hold if P, is arbitrarily close to 0. (Note that in this section we are dealing solely with s, and not at all with the u of the last section. We can therefore use R in place of R, and A in place of $ without ambiguity. The formulation of the last section led to a stronger forward theorem, but would yield a weaker converse if used here.) The proof of the following theorem is therefore the goal of this section.
T h e o r e m 3: W ith R, A, a n d P, defined as in (l), (2), a n d (3)
it is known that differences in entropy are still physically m e a n ingful as mutual informations: e.g., H(A) - H(A (B)
= Z(A ; B) (see [5] for a full development). W e m a y thus write
Z(X; YIZ) = H(XIZ) - H(XI Y,Z)
= H(XIZ) - H(XI Y) (60) since X is conditionally independent of Z given Y. Using
H(A,B)=H(A)+H(BJA)=H(B)+H(AJB), (61)
we can recast (60) as A- kp, log 6’>+ htPe) < c
H(Sk)
1
’ ’ (49)where v is the size of the source alphabet a n d C, is defined by (14).
If instead the per digit error rate pe=l/k 9 Pr (ai#zi)
i=l (50)
is used, (49) becomes
A- k[h(pe)+P&g (v--l)]
H(Sk ) I
<c
3. (51) Thus the use of this more lenient measure of reliability would not expand the region ? % .
T h e proof of this theorem will b e established through a sequence of lemmas.
L e m m a 6:
A- kpe 1s tv> + W e )
RN
1 < W N ; yNIZN) \
Nt52j
a n d
A- +tp,)+pelogtv-l)] ~ Z(X;Y[Z)
RN
1
N*
(53)Proof: F irst note that, through use of the data processing theorem 14, theorem 4.3.31 a n d F a n o ’s inequal- ity [4, theorem 4.3.11,
H($ (Z, Y) < H(S 1 Y) = G H(S I$)
< h(P,) + kP, log (v). (54) T h e n RNA= H(S IZ) from the definitions (2), (3) of R a n d A. Using (54) we obtain
RNA < H($ IZ) - H($ IZ, Y) + h(P,) + kP, log (v)
=I($; YIZ)+h(P,)+kP, log(v). (55) Since 5, X, Y, Z form a Markov chain, the data process- ing theorem implies
I($ ; YIZ) < 1(X; YIZ), (56) so
RNA < Z(X; YIZ) + h(P,) + kP, log (v) (57) which with m inor algebra establishes (52). Equation (53) is established in exactly the s a m e manner using the per digit error rate version of F a n o ’s inequality [4, theorem 4.3.21.
L e m m a 7:
Z(X; YIZ) = $log -[H(Z)-H(Y)].
(58) Proof: Although the entropy of a continuous random variable is lacking in physical significance, if we define
H(A) = - JPW 1 % [da>] d a (59
Z(X; YIZ)= [H(X)+ H(ZIX)- H(Z)]
- [H(X)+HtYlX)-H(Y)]
=H(ZIX)-H(YIX)-[H(Z)-H(Y)].
(62) Because the channel is memoryless,
H( Y[x)=igl H(YilXi)=(N/2) log (2reuf) (63) where the last expression comes from integration as in (59) [4, p. 321. Similarly
H(ZIX)=(N/2) log [2ne(u:+az)].
Substituting (63) a n d (64) into (62) yields (58).
L e m m a 8: Define
g(P) = l/2 log (2reP), P>O, g-l(a)=(1/2re)e2*,
A(o)=g[ u;+g-‘(v)] -Il.
T h e n A(u) is decreasing in 0.
Proof:
A(o)=1/2log 2 a e uz+&e2’
[ (
)I
--.Differentiating (68) yields
2 = [ e 2 ”/(2 meu,2+e2”)] - 1 G O . L e m m a 9:
(64) Q .E.D.
(65) (66) (67)
033)
(69)
H(Y)<Ng(P+uf)=(N/2) log [2ve(P+u:)]. (70) Proof: W e know that
Z(X;Y)=H(Y)-H(YjX)<NC, (71)
or
H(Y)G(N/2)log [(P+u~)/u:]+(N/2)log(2~euf)
=(N/2) log [2re(P+uf)]. (72) L e m m a IO: If
H(Y)=Nv, (73)
then
H(Z)-H(Y)>NA(u)=Ng[uf+g-l(u)]-Nv. (74) Proof See S h a n n o n [6, theorem 151, Blachman [7], a n d Bergmans [8].
456 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. IT-24, NO. 4, JULY 1978
Combining Lemmas 8; 9, and 10 we see that H(Z)-H(Y)>NA[g(P+o;)]
=Ng[u;+g-‘g(P+u:)]-Ng(P+u;)
=(N,2) log ( ‘:“:‘;“‘). (75) Using (75) with Lemma 7 yields
= N( CM - CM,) = NC,, (76) which together with Lemma 6 completes the proof of Theorem 3.
IV. DISCUSSION
It is interesting that the secrecy capacity C, = C,,, - C,, completely characterizes the achievable (R,d) region of a Gaussian wire-tap channel, just as in the case of binary symmetric channels. Motivated by this observation, Leung [9] has shown that this is true whenever both the main channel and the cascade of the main and wire-tap channels are symmetric [4, p. 941. (Strictly speaking, Leung only shows this for discrete memoryless channels.) Wyner’s results [ 11, although derived for discrete memory- less channels, can also be combined with Lemmas 8, 9, and 10 to yield Theorem 1.
In the power limited region, when P<<u2,
CM G P/( 42 In 2), (77)
C MW G P/[(u:+42 In 21, (78) and
CJC, G u;/(u:+ u;).
In the bandwidth limited region, when P>>u’, CM -I 1/2 log (P/u?),
C MWw2log [p/(u:+G)], so that
(79)
(80) (81)
c,~1/210g [(u:+u;)/u:] (82)
and
C,/C,l =o. (83)
For a fixed bandwidth C, is increasing in P, but there is a finite limit on C, no matter how large we make P. Our results are therefore of most use on power limited chan- nels. Of course, if the main channel is bandwidth limited
(P/u:>> 1) and the wire-tap channel is power limited (P/(u:+ u,‘><l), then C’/C, will be even closer to 1. It is really only the wire-tap channel that must be power limited.
There is a potential problem if the SNR’s on the chan- nels are somewhat uncertain. Then the system may oper- ate several dB below the actual capacity of the main channel, but if the wire-tap channel’s SNR is only several dB below the main channel’s nominal SNR, then secrecy is lost. In spite of this problem there may be practical applications for these results. If, for example, the wire- tapper is listening to unintentional electromagnetic radia- tion from a terminal or computer, his SNR may be tens of dB down from that of the “main channel.” Such a wire- tap channel allows almost no reduction in rate of informa- tion flow to be coupled with high uncertainty on the part of the wire-tapper.
We are currently investigating the wire-tap channel with feedback and have shown that even when the main channel is inferior to the wire-tapper’s channel it is possi- ble to transmit reliably and securely [lo]. This would obviously eliminate many of the above problems.
ACKNOWLEDGMENT
The authors wish to thank Prof. Thomas Cover and Dr.
Aaron Wyner for several valuable discussions on this problem.
111 121
I31
I41
ti/
I71
181
I91
1101
REFERENCES
A. D. Wyner, ‘The wire-tap channel,” Bell Cyst. Tech. J., vol. 54, pp. 1355-1387, Oct. 1975.
P. P. Bergmans, “Random coding theorem for broadcast channels with degraded components,” IEEE Trans. Inform Theory, vol.
IT-19, pp. 197-207, Mar. 1973.
M. E. Hellman and A. B. Carleial, “A note on Wyner’s wire-tap channel,” IEEE Trans. Inform. Theory, vol. IT-23, pp. 387-390, May 1977.
R. G. Gallager, Information Theory and Reliable Communication.
New York: Wiley, 1968.
R. Ash, Information Theory. New York: Interscience, 1965.
C. E. Sharmon, “A mathematical theory of communication,” Bell
Syst. Tech. J., vol. 27, pp. 623-656, 1948.
N. M. Blachman, “The convolution inequality for entropy powers,” IEEE Trans. Inform Theory, vol. IT-I 1, pp. 267-271,
Apr. 1965. _ --
P. P. Bergmans, “A simple converse for broadcast channels with additive white Gaussian noise.” IEEE Trans. Inform Theory. vol.
IT-20, pp. 279-280, Mar. 1974. _
S. K. Leung-Yan-Cheong, “On a special class of wire-tap chan- nels,” IEEE Trans. Inform Theory, vol. IT-23, pp. 625-627, Sept.
1977.
S. K. Leung-Yan-Cheong, Multi-User and Wire-tq Channels In- cludina Feedback. Ph.D. thesis. Stanford Universitv. Stanford. CA.
1976. -