Allgemeiner ist eine Umgebung U von x eine Menge, die eine ε-Umgebung B ε (x ) enth¨ alt.
Volltext
Abbildung
ÄHNLICHE DOKUMENTE
• Selbst wenn Sie eine Denition oder eine Aussage kennen, hilft es, sich diese mit Beispie- len zu veranschaulichen. • Manche Aussagen lassen sich leichter per Widerspruchsbeweis
Peter Junghanns Technische Universit¨ at Chemnitz Dr. Ralf Hielscher Fakult¨ at f¨ ur Mathematik.. PD Dr.. Die Menge aller Randpunkte von A bezeichnen wir mit ∂A. abgeschlossen)
Bool mit false < true ist
[r]
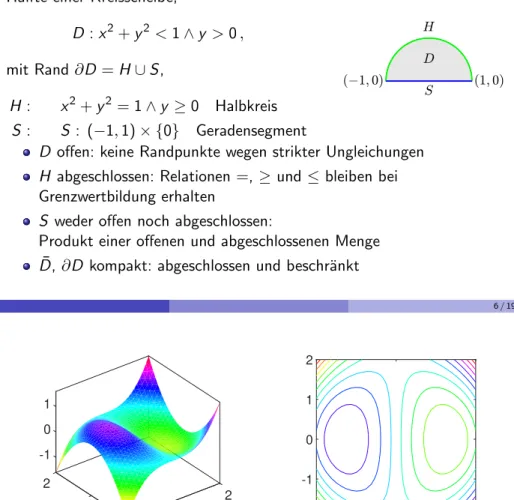
Eine hinreichende Bedingung f¨ ur ein lokales Minimum (Maximum) in einem kritischen Punkt x ∗ im Innern des Definitionsbereichs D ist, dass ebenfalls die zweiten partiellen
Eine hinreichende Bedingung f¨ ur ein lokales Minimum (Maximum) in einem kritischen Punkt x ∗ im Innern des Definitionsbereichs D ist, dass ebenfalls die zweiten partiellen