Equational Termination by Semanti Labelling
HitoshiOhsaki 1
,AartMiddeldorp 2
, andJurgenGiesl 3
1
ComputerSieneDivision,EletrotehnialLaboratory
Tsukuba305-8568, Japan
ohsakietl.go.jp
2
InstituteofInformationSienesandEletronis
UniversityofTsukuba,Tsukuba305-8573,Japan
amiis.tsukuba.a.jp
3
ComputerSieneDepartment
UniversityofNewMexio,Albuquerque,NM87131,USA
giesls.unm.edu
Abstrat. Semantilabellingisapowerfultoolforprovingtermination
oftermrewrite systems.The usefulnessof the extensionto equational
termrewriting desribed inZantema [24℄ is howeverratherlimited. In
this paperwe introdueastronger version ofequational semantial la-
belling,parameterized bythreehoies:(1)theorderontheunderlying
algebra(partial ordervs.quasi-order),(2)the relationbetweenthe al-
gebraand the rewrite system (modelvs.quasi-model),and (3)the la-
bellingofthefuntionsymbolsappearingintheequations(forbiddenvs.
allowed).Wepresentsoundnessandompletenessresultsforthevarious
instantiationsandanalyzetherelationshipsbetweenthem.Appliations
ofourequationalsemantilabellingtehniqueinludeashortproofofthe
mainresultofFerreiraetal.[7℄|theorretnessofaversionofdummy
eliminationforAC-rewritingwhihompletelyremovestheAC-axioms|
andanextensionofZantema'sdistributioneliminationtehnique[23℄to
theequationalsetting.
1 Introdution
This paper is onerned with termination of equationalterm rewrite systems.
Terminationofordinarytermrewritesystemshasbeenextensivelystudied and
several powerful methods for establishing termination are available (e.g. [1,4,
21℄).Forequationaltermrewritingmuhlessisknown,althoughinreentyears
signiantprogresshasbeenmadewith respetto AC-termination,i.e., termi-
nationof equationalrewritesystemswhere the set ofequations onsists ofthe
assoiativityandommutativityaxiomsAC(f)=ff(f(x;y);z)f(x;f(y;z));
f(x;y) f(y;x)g for (some of) the binary funtion symbols ourring in the
rewrite rules. An early paper ontermination ofequational rewriting is Jouan-
naud andMu~noz[11℄.Inthat papersuÆientonditionsaregivenforreduing
?
Proeedings of the Annual Conferene of the European Assoiation for Computer
SieneLogi(CSL'00),Fishbahau,Germany,LNCS1862,pp.457-471,2000.
ingtermrewritesystem.Inanotherearlypaper(BenCherifaandLesanne[2℄)
aharaterizationofthepolynomialsisgiventhat anbeused inapolynomial
interpretation proof of AC-termination. In morereentpapers[12,19{21℄syn-
tatimethodslikethewell-knownreursivepathorderforprovingtermination
of rewriting are extended to AC-rewriting. Marhe and Urbain [14℄ extended
thepowerfuldependeny pairtehniqueof Artsand Giesl[1℄to AC-rewriting.
In [6,7℄twoextensions of dummy elimination([8℄) to equationalrewriting are
presented.In[15℄ the typeintrodutiontehniqueof Zantema [23℄ isextended
to equationaltermrewriting.
Inthis paper weextend another tehnique of Zantema to equational term
rewriting.Bylabellingfuntionsymbolsaordingtothesemantisoftherewrite
system,semantilabelling([24℄)transformsarewritesystemintoanotherrewrite
systemwiththesameterminationbehaviour.Theaimistoobtainatransformed
rewritesystemwhereterminationiseasiertoestablish.Thestrengthofsemanti
labelling is amply illustrated in [16,24℄. Here we present powerful extensions
of semanti labelling to equationalrewriting and analyze their soundness and
ompleteness.Ourequationalsemantilabellingyieldsashortorretnessproof
of aversionof dummy elimination forAC-rewriting. This result of Ferreiraet
al. was obtained in [7℄ by onsiderably more ompliated arguments. Another
appliationofourtehniqueistheextensionofsomeoftheresultsofZantema[23℄
onerningdistributioneliminationto theACase.
2 Preliminaries
Familiarity with the basis of term rewriting ([3℄) is assumed. An equational
system(ESforshort)onsistsofasignatureF andasetE ofequationsbetween
terms in T(F;V). We write s !
E
t if there exist an equation l r in E,
a substitution , and a ontext C suh that s = C[l℄ and t = C[r℄. The
symmetri losureof !
E
is denoted by `a
E
andthe transitivereexivelosure
of `a
E by
E
. A rewriterule is anequation lr suh that l isnot avariable
andvariableswhihourinralsoourinl.Rewriteruleslrarewrittenas
l!r.A term rewrite system (TRSforshort) isan ESwith theproperty that
allitsequationsarerewriterules.Anequationaltermrewritesystem (ETRSfor
short)R=E onsistsofaTRSRandanESE overthesamesignature.Wewrite
s!
R=E
tifthere existtermss 0
andt 0
suhthat s
E s
0
!
R t
0
E
t.Similarto
ordinarytermrewritesystems,anETRSisalled terminating ifthere doesnot
exist aninnite!
R=E
redution.
LetF beasignatureand A=(A;ff
A g
f2F
) anF-algebraequippedwitha
quasi-order (i.e., areexive and transitiverelation) %on its (non-empty) ar-
rier A. For any variable assignment : V ! A we dene the term evaluation
[℄
A
: T(F;V) ! A indutively by [℄
A
(x) = (x) and [℄
A (f(t
1
;:::;t
n )) =
f
A ([℄
A (t
1
);:::;[℄
A (t
n
))for x 2 V, f 2F, andt
1
;:::;t
n
2 T(F;V). If A is
lear from the ontext, then we often write [℄ instead of [℄
A
. We say that
A ismonotone ifthe algebraoperationsof Aare monotone withrespetto %
A 1 i n
f
A (a
1
;:::;b;:::;a
n
) for all a
1
;:::;a
n
;b 2 A and i 2 f1;:::;ng with a
i
% b.
An ETRS R=E over a signature F is ompatible with a monotone F-algebra
(A;%) ifl%
A
rforeveryrewriterulel!r2Randl
A
rforeveryequation
l r 2 E. Here the relation %
A
is dened by s %
A t if [℄
A
(s)% [℄
A (t) for
everyassignmentand
A
is theequivalenerelationindued by %
A
.If R=E
and(A;%)areompatible,wealsosaythat(A;%)isaquasi-model ofR=E.We
all(A;%)amodel ofR=E ifl
A
rforalll!r2Randlr2E.
ATRSRispreedeneterminatingifthereexistsawell-foundedorder=on
itssignatureFsuhthatroot(l)=f foreveryrulel!r2Randeveryfuntion
symbolf ourring in r. Preedene terminating TRSs are terminating ([16℄).
Thenextlemma statesthat thisremainstrueinthepreseneofAC-axioms.
Lemma1. LetR=EbeanETRSoverasignatureFsuhthatE= S
f2G AC(f)
forsomesubsetG ofF.IfRispreedeneterminatingthenR=E isterminating.
Proof. Bydenitionthereisawell-foundedorder=onF suhthat root(l)=f
for every rule l ! r 2 R and every funtion symbol f ourring in r. Any
AC-ompatiblereursivepathorderinduedby=thatisdenedontermswith
variables(e.g.[13,19℄)orientstherulesofRfromlefttoright.(Theompliated
aseinwhihtwotermswithequalrootsymbolsinGhavetobeomparednever
arisesduetotheassumptionon=.)WeonludethatR=E is terminating. ut
3 Semanti Labelling for Equational Rewriting
Inthissetionwepresentourequationalsemantilabellingframeworkbyappro-
priatelyextendingthedenitionsofZantema[24℄forordinarysemantilabelling.
Denition1. Let F be a signature and A an F-algebra. A labelling L for F
onsists of sets of labels L
f
A for every f 2 F.The labelledsignature F
lab
onsists of n-ary funtion symbols f
a
for every n-ary funtion symbol f 2 F
and label a2 L
f
together with all funtion symbols f 2 F suh that L
f
= ?.
A labelling ` for A onsists of a labelling L for the signature F together with
mappings `
f : A
n
!L
f
for every n-ary funtion symbol f 2F with L
f
6=?.If
A isequipped with aquasi-order %then the labellingis said tobe monotone if
itslabellingfuntions`
f
aremonotone(with respetto%)in allarguments.
Denition2. LetR=E be an ETRS overasignature F,(A;%) anF-algebra,
and`alabellingfor A.Foreveryassignmentweindutivelydene alabelling
funtion lab
from T(F;V) to T(F
lab
;V): lab
(t) =t if t 2 V and lab
(t)=
f
`f([℄(t1);:::;[℄(tn)) (lab
(t
1
);:::;lab
(t
n
)) if t = f(t
1
;:::;t
n
). We dene TRSs
R
lab
,De(F;) andESsE
lab
,Eq(F;) overthesignatureF
lab
asfollows:
R
lab
=flab
(l)!lab
(r)jl!r2Rand:V!Ag;
E
lab
=flab
(l)lab
(r)jlr2E and:V!Ag;
De(F;)=ff
a (x
1
;:::;x
n )!f
b (x
1
;:::;x
n
)jf 2F;a;b2L
f
; abg;
Eq(F;)=ff
a (x
1
;:::;x
n )f
b (x
1
;:::;x
n
)jf2F;a;b2L
f
;ab;a6=bg:
trivial equations. When the signature F and the quasi-order %an be inferred
from the ontextwe just writeDe and Eq.We write Rfor the union of R
lab
andDeandE for the unionofE
lab
andEq.
Thenexttheoremstatesourrstequationalsemantilabellingresult.
Theorem1. LetR=E beanETRS overasignatureF,(A;%) amonotoneF-
algebra, and ` a monotone labelling for A. If A is a quasi-model of R=E and
R=E isterminatingthenR=E isterminating.
Proof. Weshowthatforalltermss;t2T(F;V)andassignmentswehave
1. ifs!
R
tthenlab
(s)
E
+
!
R lab
(t),
2. ifs`a
E
tthenlab
(s)
E lab
(t).
Supposes=C[l℄andt=C[r℄forsomerewriterulel!r2R,ontextC,and
substitution.Weshow(1)byindutiononC.IfC=thenlab
(s)=lab
(l)
and lab
(t) =lab
(r). Dene the assignment =[℄
A
Æ and thesubstitu-
tion = lab
Æ (i.e., is applied rst). An easy indution proof (e.g. [23,
Lemma 2℄) reveals that lab
(l)=lab
(l) and lab
(r)=lab
(r). Byde-
nitionlab
(l)!lab
(r)2R
lab
andhenelab
(s)=lab
(l) !
Rlab lab
(r) =
lab
(t).Fortheindutionstep,letC=f(u
1
;:::;C 0
;:::;u
n
).Theindutionhy-
pothesisyieldslab
(C
0
[l℄)
E
+
!
R lab
(C
0
[r℄).BeauseAisaquasi-model
ofR=E and C 0
[l℄!
R C
0
[r℄,wehave[℄
A (C
0
[l℄)%[℄
A (C
0
[r℄).Let
a=`
f ([℄
A (u
1
);:::;[℄
A (C
0
[l℄);:::;[℄
A (u
n ))
and
b=`
f ([℄
A (u
1
);:::;[℄
A (C
0
[r℄);:::;[℄
A (u
n )):
Monotoniityofthelabellingfuntion`
f
yieldsa%b.Wedistinguishtwoases.
Ifabthen
lab
(s)
E
+
!
R f
a (lab
(u
1
);:::;lab
(C
0
[r℄);:::;lab
(u
n ))
!
De f
b (lab
(u
1
);:::;lab
(C
0
[r℄);:::;lab
(u
n ))
= lab
(t):
Ifabthen
lab
(s)`a
=
Eq f
b (lab
(u
1
);:::;lab
(C
0
[l℄);:::;lab
(u
n ))
E
+
!
R f
b (lab
(u
1
);:::;lab
(C
0
[r℄);:::;lab
(u
n ))
= lab
(t):
Here`a
=
Eq
denotes`a
Eq
[=.Sine
E
+
!
R !
De
E
+
!
R and`a
=
Eq
E
+
!
R
E
+
!
R
,inbothasesweobtainthedesiredlab
(s)
E
+
!
R lab
(t) .
Theproofof (2)followsalongthesamelines. Intheindution stepwehave
[℄
A (C
0
[l℄) [℄
A (C
0
[r℄). Monotoniity of `
f
yields both a %b and b % a.
Hene ab andthus
lab
(s)= f
a (lab
(u
1
);:::;lab
(C
0
[l℄);:::;lab
(u
n ))
`a
=
Eq f
b (lab
(u
1
);:::;lab
(C
0
[l℄);:::;lab
(u
n ))
E f
b (lab
(u
1
);:::;lab
(C
0
[r℄);:::;lab
(u
n ))
= lab
(t)
From(1)and(2)itfollowsthatanyinniteR=E-rewritesequenegivesrise
toaninniteR =E-rewritesequene. ut
Theonverseoftheabovetheoremdoesnothold.Considertheterminating
ETRS R=E with R= ? and E = ff(a) ag. Let A be the algebra overthe
arrierf0;1gwith10andoperationsf
A
(x)=xforallx2f0;1ganda
A
=1.
Note that A is a(quasi-)model of R=E. By letting `
f
bethe identity funtion
and by hoosing L
a
= ?, weobtain the labelled ETRS R=E with R
lab
= ?,
De=ff
1 (x)!f
0 (x)g,E
lab
=ff
1
(a)ag,andEq=?.TheETRS R =E isnot
terminating: a
Elab f
1 (a) !
De f
0 (a)
Elab f
0 (f
1 (a)) !
De
Nevertheless, in
thisexampletherearenoinniteR =E-rewritesequenesthatontaininnitely
many R
lab
=E-steps,whih is known astherelative termination (Geser[10℄) of
R
lab
=E withrespettoDe.ItisnotdiÆulttoshowthatundertheassumptions
ofTheorem1terminationofR=EisequivalenttorelativeterminationofR
lab
=E
withrespetto De.
Zantema [24℄ showed theneessityof theinlusion ofDe inRfor theor-
retness of Theorem 1(with E = ?) by means of the TRS R = ff(g (x)) !
g (g (f(f(x))))g, the algebraAoverthearrier f0;1g withoperationsf
A (x)=1
andg
A
(x)=0forallx2f0;1g,andtheorder10.Bylabellingfwiththevalue
ofitsargument,weobtaintheTRSR
lab
=ff
0
(g (x))!g (g (f
1 (f
0 (x))));f
0 (g (x))
!g (g (f
1 (f
1
(x))))gwhihisompatiblewiththereursivepathorderwithpree-
denef
0
=f
1
;g .However,Risnotterminating:f(f(g (x)))!f(g (g (f(f(x)))))!
g (g (f(f(g (f(f(x)))))))!
Theinlusion of Eq in E isalso essentialfor theorretness ofTheorem 1.
ConsidertheETRSR=E withR=ff(a;b;x)!f(x;x;x);g (x;y)!x;g (x;y)!
yg and E = ?. Let A be the algebra over the arrier f0;1g with 0 1 and
operationsf
A
(x;y;z)=1,g
A
(x;y)=0,a
A
=0,andb
A
=1.Welabelfuntion
symbolf as follows: `
f
(x;y;z) =0 if x = y and `
f
(x;y;z) =1 if x 6= y. Note
that Ais aquasi-modelforR=E and `
f
is triviallymonotone.WehaveR
lab
=
ff
1
(a;b;x) ! f
0
(x;x;x);g (x;y) ! x;g (x;y) ! yg, De = ?, and E
lab
= ?.
Terminationof Riseasily shown.It iswell-known(Toyama[22℄)thatRisnot
terminating.NotethatinthisexampleEq=ff
0
(x;y;z)f
1
(x;y;z)gandhene
R=E isnotterminating.
Finally,bothmonotoniityrequirementsareessential.ConsidertheTRSR=
ff(g (a)) ! f(g (b));b ! ag. Let A be the algebraoverthe arrier f0;1g with
1 0 and operations f
A
(x) = 0, g
A
(x) = 1 x, a
A
= 0, and b
A
= 1. We
have l %
A
r for both rules l ! r 2 R. If `
f
(x) = x then weobtain the TRS
R= ff
1
(g (a))! f
0
(g (b));b ! a;f
1
(x) !f
0
(x)gwhih is ompatible with the
reursivepath order withpreedene f
1
=f
0
;g and f
1
=b=a. However,R is
not terminating. Note that g
A
is not monotone. Next onsider the algebra B
overthearrierf0;1gwith10and operationsf
B
(x)=0,g
B
(x)=x,a
B
=0,
and b
B
=1.If`
f
(x)=1 x then weobtainthe sameTRS Rasbefore. Note
that now`
f
isnotmonotone.
If the algebra A is a model of the ETRS R=E then (similar to ordinary
semantilabelling [24℄) we an dispense with De. Moreover, in this ase the
Theorem2. Let R=E be an ETRS over a signature F, (A;%) a monotone
F-algebra, and ` amonotonelabelling for A. If A isa model of R=E thenter-
mination of R
lab
=E isequivalenttoterminationof R=E.
Proof. Thefollowingstatementsareobtainedbyastraightforwardmodiation
oftheproofofTheorem1:
1. ifs!
R
tthenlab
(s)
E !
Rlab lab
(t),
2. ifs`a
E
tthenlab
(s)
E lab
(t).
Note that sine A is a model we have [℄
A (C
0
[l℄) [℄
A (C
0
[r℄) and hene
a b in the indution step. This explains why there is no need for De. So
termination of R
lab
=E implies termination of R=E. The onverse also holds;
eliminating all labels in an innite R
lab
=E-rewrite sequene yields an innite
R=E-rewritesequene(beausethere areinnitelymanyR
lab
-steps). ut
Ifthequasi-modelA in Theorem1is equipped withapartial order (i.e.,a
reexive, transitive,andanti-symmetrirelation)insteadof aquasi-order%
thenwean dispensewithEq.
Theorem3. LetR=E beanETRS overasignatureF,(A;) amonotoneF-
algebra, and ` a monotone labelling for A. If A is a quasi-model of R=E and
R=E
lab
isterminatingthen R=E isterminating.
Proof. TheproofofTheorem1applies;beausetheequivaleneassoiatedwith
apartialorderistheidentityrelationwehaveEq=?. ut
TherstexampleinthissetionshowsthattheonverseofTheorem3does
nothold.Combiningthepreedingtwotheoremsyieldsthefollowingresult.
Corollary 1. Let R=E be an ETRS over a signature F, (A;) a monotone
F-algebra, and ` amonotonelabelling for A. If A isa model of R=E thenter-
mination of R
lab
=E
lab
isequivalent toterminationofR=E. ut
Notethatifthepair(A;)isamodelofR=E thensois(A;=).Sineinthis
asemonotoniityofboththealgebraoperationsandthe labellingfuntions is
triviallysatised,weanrephrasetheaboveorollaryasfollows.
Corollary 2. Let R=E be an ETRS overa signature F, A an F-algebra, and
` a labelling for A. If A is a model of R=E then termination of R
lab
=E
lab is
equivalent totermination ofR=E. ut
Notethattheunspeiedquasi-orderisassumedtobetheidentityrelation,
somodelheremeansl=
A
rforallrulesl!r2Randallequationslr2E.
Letusonludethissetionbyillustratingthepowerofequationalsemanti
labelling onaonrete example.ConsidertheETRS R=E withR=fx 0!
x;s(x) s(y) ! x y;0s(y) ! 0;s(x)s(y) ! s((x y)s(y))g and
order>,andoperations0
A
=0,s
A
(x)=x+1,andx
A
y=x
A
y=x.This
algebraisaquasi-modelofR=E. If`
(x;y)=xthenwehaveR
lab
=fx 0!
x;s(x) s(y)!x y;0
0
s(y)!0g[fs(x)
n+1
s(y)!s((x y)
n s(y))j
n > 0g, De = fx
m
y ! x
n
y j m > ng, and E
lab
= f(x
n y)
n z
(x
n z)
n
y j n >0g. Termination of R=E
lab
anbeshown by the following
polynomial interpretation: [0℄ = 0, [s℄(x) = x+1, x[ ℄y = x+y +1, and
x[
n
℄y = x+ny+n+y for all n >0.Aording to Theorem 3the original
ETRS R=E is terminating as well. Note that a diret termination proof with
standardtehniquesisimpossiblesineaninstane ofthelastruleof Risself-
embedding.Inordertomakethisrulenon-self-embeddingitisessentialthatwe
label.ThisexplainswhyZantema'sversionofequationalsemantilabelling|
presentedin thenextsetion|willfailhere.
4 Semanti Labelling Cube
Theoriginalversionof equationalsemantilabellingdesribedin Zantema [24℄
ispresentedbelow.
Theorem4 ([24℄).LetR=E beanETRS overasignature F,AanF-algebra,
and`alabellingforAsuhthatfuntion symbolsourring inE areunlabelled.
If AisamodelofR=E thenterminationofR
lab
=E isequivalent totermination
of R=E. ut
In[24℄itisremarkedthattherestritionthatsymbolsinE areunlabelledis
essential.Corollary2,ofwhihTheorem4isanimmediateonsequene,shows
that this is nottrue. Zantema provides the non-terminating ETRS R=E with
R=f(x+y)+z !x+(y+z)g and E =fx+y y+xg, and themodel A
onsistingofthepositiveintegersN
+
withthefuntionsymbol+interpretedas
addition.Bylabelling+with thevalueofitsrstargument,weobtainR
lab
=
f(x+
i y)+
i+j
z!x+
i (y+
j
z)ji;j2N
+
gandE
lab
=fx+
i
yy+
j
xji;j2
N
+
g.Aordingto Corollary2thelabelledETRS R
lab
=E
lab
is notterminating
andindeedthere areinniterewritesequenes,e.g.
(x+
1 x)+
2
x!x+
1 (x+
1
x)(x+
1 x)+
2
x!
In [24℄ it is remarked that R
lab
=E 0
with E 0
= fx+
i
y ! y+
i
x j i 2 N
+ g is
terminating,sineitisompatible withthepolynomialinterpretationin whih
the funtion symbol +
i
is interpreted as addition plus i, for every i 2 N
+ .
However,E 0
isnot alabelledversionofE.
Thevariousversionsofequationalsemantilabellingpresentedabovedier
in three hoies:(1) theorder onthealgebraA(partialorder vs.quasi-order),
(2) the relation between the algebra A and the ETRS R=E (model vs. quasi-
model),and(3)thelabellingofthefuntion symbolsappearinginE (forbidden
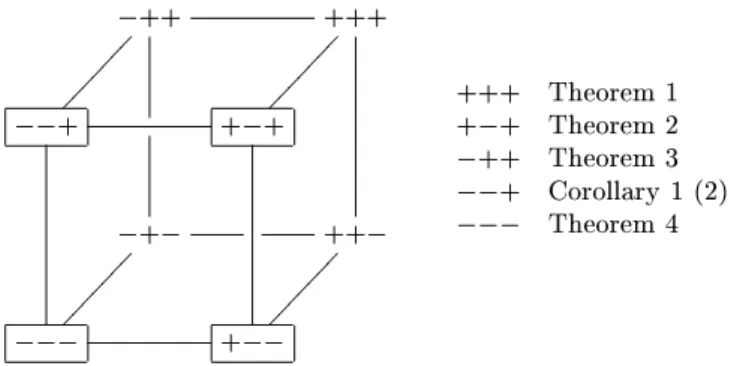
vs.allowed).Thisnaturallygivesrisetotheubeofeightversionsofequational
semantilabelling possibilities shown in Figure 1.Everypossibility is given as
so ++denotestheversionofequationalsemantilabellingwithpartialorder,
quasi-model,and(possibly)labelledfuntionsymbolsinE.Alleightversionsof
equationalsemantilabellingaresound, i.e., termination ofthelabelled ETRS
implies termination of the original ETRS. The versions in whih termination
of the labelled ETRS is equivalent to termination of the original ETRS are
indiatedbyasurroundingbox.
++ +++
+ + +
+ ++
+
+++ Theorem1
+ + Theorem2
++ Theorem3
+ Corollary1(2)
Theorem4
Fig.1.Equationalsemantilabellingube.
Wepresentone moreversionof equationalsemantilabelling, stating that
the impliation of Theorem 1 beomes an equivalene in the speial ase that
E is variablepreserving (i.e., everyequationl r 2E hasthepropertythat l
and r have the samenumber of ourrenesof eah variable), the(strit part
of the) quasi-order%is well founded,and funtion symbolsourring in E are
unlabelled.Inotherwords,ifEisvariablepreserving(whihinpartiularistrue
for AC)and the quasi-order %is well foundedthen wean put a boxaround
++ in Figure 1. Before presenting the proof, we show the neessity of the
threeonditions.FirstonsidertheETRSR=E withR=?andE =ff(x;x)
xg where the signature ontainsa unary funtion symbolg in addition to the
funtion symbolf. LetAbethealgebraoverthearrierf0;1g with10and
operationsf
A
(x;y)=xandg
A
(x)=x.NotethatAisa(quasi-)modelofR=E.
Bylabellingg with the valueof its argument, we obtainthe ETRS R=E with
R=De=fg
1
(x)!g
0
(x)gandE=E.TheETRSR=Eistriviallyterminating,
but R =E admitsthefollowinginniterewritesequene:
g
1
(x)f(g
1 (x);g
1
(x))!f(g
0 (x);g
1
(x))f(g
0 (x);f(g
1 (x);g
1
(x)))!
Notethat E isnotvariablepreserving.Theneessityofthewell-foundednessof
the quasi-order% followsby onsidering theterminating TRS R=E with R=
ff(x)!g (x)gandE=?,thealgebraAoverthearrierZwithstandardorder
>and operationsf
A (x) =g
A
(x)=x,and thelabelling`
f
(x)=x.In thisase
wehaveR
lab
=ff
i
(x)!g (x)ji2ZgandDe=ff
i (x)!f
j
(x)ji>jg,soR
E mustbeunlabelledisjustiedbytheounterexamplefollowingTheorem1.
Theorem5. Let R=E be an ETRS over a signature F with E variable pre-
serving, (A;%) amonotone F-algebra with % well-founded, and ` a monotone
labelling for (A;%) suh that funtion symbols ourring in E areunlabelled. If
Aisaquasi-modelofR=E thenterminationofR=E isequivalenttotermination
of R=E.
Proof. First notethat R =E =(R
lab
[De )=(E[Eq)beausefuntion symbols
ourringinE areunlabelled.The\if"partisaonsequeneofTheorem1.For
the\only if"partweshowthat the ETRSDe=(E[Eq)is terminating.Fora
termt2T(F
lab
;V)let(t)denotethemultisetofalllabelsourringin t.The
followingfats arenotdiÆulttoshow:
{ ifs!
De
tthen(s)
mul (t),
{ ifs`a
Eq
tthen(s)
mul (t),
{ ifs`a
E
tthen(s)=(t).
Here
mul
denotesthemultisetextensionof([5℄)and
mul
denotesthemulti-
setextensionoftheequivalenerelation(whihoinideswiththeequivalene
relation assoiated with the multisetextension %
mul
of %, see e.g.[17, Deni-
tion5.6℄).ForthevalidityofthelastobservationitisessentialthatEisvariable
preservingandthatfuntionsymbolsourringin E areunlabelled. Fromthese
fatsandthewell-foundednessof%
mul
weobtaintheterminationofDe=(E[ Eq).
Now,ifR =E isnotterminatingthenitadmitsaninniterewritesequenewhih
ontains innitely many R
lab
-steps. Erasingall labels yields an innite R=E-
rewritesequene,ontraditingtheassumptionthatR=E is terminating. ut
5 Dummy Elimination for Equational Rewriting
Ferreira,Kesner,andPuel [7℄extendeddummyelimination[8℄toAC-rewriting
byompletelyremovingtheAC-axioms.Weshowthat theirresultiseasilyob-
tained in our equational semanti labelling framework. Our denition of
dummy (R) isdierentfromtheonein[7,8℄,buteasilyseentobeequivalent.
Denition3. Let R be a TRS over a signature F. Let e be a distinguished
funtion symbolin F of aritym>1andletbeafreshonstant.WewriteF
for(Fnfeg)[fg.Themappingap: T(F;V)!T(F
;V)isindutivelydened
as follows: ap(t)=t if t2V,ap(e(t
1
;:::;t
m
))=, andap(f(t
1
;:::;t
n ))=
f(ap(t
1
);:::;ap(t
n
))if f 6=e.Themapping dummy assignstoevery term in
T(F;V)asubset ofT(F
;V):
dummy (t)=fap(t)g[fap(s)js isanargumentofan esymbol intg:
Finally, wedene
dummy (R)=fap(l)!r 0
jl!r2Randr 0
2dummy (r) g:
havefewervariablesthanl.Inthatase,however,dummy (R)isnotterminating
andtheresultspresentedbelowholdvauously.FerreiraandZantema[8℄showed
that ifdummy (R)is terminatingthenRisterminating.Asimpleproofof this
fat using self-labelling, a speial ase of semanti labelling, an be found in
Middeldorpet al.[16℄.Twoextensionsofthis resulttoequationalrewritingare
known.In[6℄FerreirashowedthatterminationofR=E followsfromtermination
ofdummy (R)=EprovidedthatEisvariablepreservinganddoesnotontainthe
funtionsymbole.TheextensionpresentedinFerreiraetal.[7℄isstatedbelow.
Theorem6. LetR=E beanETRS withE=AC(e).If dummy (R)isterminat-
ingthen R=E isterminating.
Inotherwords,AC-terminationofRisreduedtoterminationofdummy (R).
Proof. We turn the set of terms T(F
;V) into an F-algebra A by dening
e
A (t
1
;:::;t
n
)=andf
A (t
1
;:::;t
n )=f(t
1
;:::;t
n
)forallother funtion sym-
bolsf 2Fandtermst
1
;:::;t
n 2T(F
;V).WeequipAwiththe(well-founded)
partialorder=!
dummy(R)
.OneanverifythatAismonotonewithrespetto
.Aneasyindutionproofshowsthat[℄(t)=ap(t)foralltermst2T(F;V).
Weshowthat Aisaquasi-modelofR=E.Let:V !T(F
;V)beanarbitrary
assignmentandletl!r2R.Wehave[℄(l)=ap(l)and[℄(r)=ap(r)by
theaboveproperty.Therewriteruleap(l)!ap(r) belongsto dummy (R)by
denition andhene[℄(l)[℄(r).Forthetwoequationslr2E welearly
have[℄(l)==[℄(r).HeneAisaquasi-modelofR=E.
Denethe(monotone)labelling`asfollows:`
f
=f
A
forallfuntionsymbols
f 2F.AordingtoTheorem3itissuÆienttoshowthatR =E
lab
isterminating.
Dene apreedene =on F
lab
asfollows: f
s
=g
t
if andonly ifs ([B) +
t,
whereBisthepropersupertermrelation.Notethat=inheritswell-foundedness
from.WelaimthatRispreedeneterminating withrespetto=.Rewrite
rulesinDeareoftheformf
s (x
1
;:::;x
n )!f
t (x
1
;:::;x
n
)withstandthus
f
s
=f
t
.ForrulesinR
lab
wemakeuseofthefollowingproperty:
iftErthenap(t)Er 0
forsometermr 0
2dummy (r). ()
Nowletl!r2R
lab
.Bydenitionthereexistanassignment:V !T(F
;V)
and arewrite rule l 0
! r 0
2 R suh that l = lab
(l
0
) and r = lab
(r
0
). The
labeloftherootsymboloflis[℄(l 0
)=ap(l 0
).Letsbethelabelofafuntion
symbol in r. By onstrution s = [℄(t) = ap(t) for some subterm t of r 0
.
Aording to (1)wehaveap(t) Er 0 0
forsomer 0 0
2dummy (r 0
).By denition
ap(l 0
) ! r 0 0
2 dummy(R) and hene ap(l 0
) r 0 0
D ap(t) = s. Conse-
quently,root(l)=f foreveryfuntionsymbolf inr.Thisompletestheproofof
preedeneterminationofR .SineE
lab
=AC(e
),terminationofR =E
lab follows
fromLemma 1. ut
Thereaderisinvitedtoompareourproofwiththeonein[7℄.Fortheabove
simpleproofweindeed neededournewpowerfulversionofequationalsemanti
labelling,i.e.,Zantema'srestritedversion(Theorem4)wouldnothaveworked.
dummyeliminationpresentedin[6℄analsobesimpliedbyequationalsemanti
labelling.Thisturnsoutnottobethease.Onereasonisthatfuntionsymbols
ofEthatalsoappearinRwillbelabelled,ausingE
lab
(andE)tobeessentially
dierent from E. In partiular, if E onsists of AC-axioms then E
lab
ontains
non-AC axioms and hene AC-ompatible orders are not appliable to R=E.
Moreover,Lemma1doesnotextendtoarbitraryESsEanditisunlearhowto
hangethedenition ofpreedenetermination suhthat itdoes.
Reently, Nakamuraand Toyama[18℄ improved dummy elimination by re-
stritingr 0
inthedenition ofdummy (R)totermsin(dummy(r)nT(F
C
;V))[
fap(r)g with F
C
denoting the onstrutors of R. In other words, elements
of dummy (r)nfap(r)g that do not ontain a dened funtion symbol need
not be onsidered when forming the right-hand sides of the rewrite rules in
dummy (R). For example, the TRS R = ff(a) ! f(b);b ! e(a)g is trans-
formedintothenon-terminatingTRSdummy(R)=ff(a)!f(b);b!;b!ag
by dummyelimination whereas theabove improvementyields theterminating
TRS ff(a) ! f(b);b ! g. Aoto 1
suggested that a further improvement is
possiblebystripping otheoutermostonstrutor ontextof everyelementin
dummy (r)nfap(r)g. ForR=ff(a(x))!f(b);b!e(a(f()))gthiswouldyield
theterminatingTRSff(a(x))!f(b);b!;b!f()gwhereasthetransforma-
tionof [18℄produesdummy (R) =ff(a(x))!f(b);b!;b!a(f())g,whih
islearlynotterminating.
Theseideasareeasily inorporatedinourdenition ofdummy elimination.
HereF
D
=FnF
C
denotesthedened symbolsofR.
Denition4. Let Rbe aTRS over asignature F. The mapping dummy 0
as-
signs toeveryterm inT(F;V)asubset ofT(F
;V),asfollows:
dummy 0
(t)=ap(t)[
ap(s)
sisamaximalsubterm of anargument
ofein tsuhthat root(s)2F
D nfeg
:
Wedene
dummy 0
(R)=fap(l)!r 0
jl!r2Randr 0
2dummy 0
(r)g:
Theorem7. Let R=E be an ETRS with E =AC(e). If dummy 0
(R) is termi-
natingthen R=E isterminating.
Proof. VerysimilartotheproofofTheorem6.Thediereneisthatwedonot
label thefuntion symbolsin F
C
. Inorderto obtainpreedenetermination of
Rweextendthepreedene=onF
lab byf
t
=gforeveryf 2F
D
,t2T(F
;V),
andg2F
C
.Inaddition,() isreplaedbythefollowingproperty:
iftErandroot(t)2F
D
thenap(t)Er 0
forsometermr 0
2dummy 0
(r).
Taking these hanges into onsideration, termination of R=E is obtainedasin
theproofofTheorem6. ut
1
Remarkmadeatthe14thJapaneseTermRewritingMeeting,NaraInstituteofSi-
eneandTehnology,Marh15{16,1999.
Nextweshowthatourresultsonequationalsemantilabellinganalsobeused
to extend the distribution elimination transformation of [23℄ to the AC ase.
Again, for that purpose we need our powerful version of equational semanti
labelling, i.e., Theorem4doesnot suÆe.LetRbeaTRS overasignature F
and let e 2 F be a designated funtion symbol whose arity is at least one. A
rewriterulel!r2Risalled adistribution rule foreifl=C[e(x
1
;:::;x
m )℄
and r = e(C[x
1
℄;:::;C[x
m
℄) for some non-empty ontext C in whih e does
not ourand pairwise dierent variables x
1
;:::;x
m
. Distribution elimination
isatehniquethattransformsRbyeliminating alldistributionrulesfor eand
removingthesymbolefromtheright-handsidesoftheotherrules.LetF
distr
=
F nfeg. We indutively dene amapping distr that assigns to everyterm in
T(F;V)anon-emptysubsetofT(F
distr
;V),asfollows:
distr(t)= 8
>
>
>
<
>
>
>
:
ftg ift2V;
m
[
i=1 distr(t
i
) ift=e(t
1
;:::;t
m );
ff(s
1
;:::;s
n )js
i
2distr(t
i
)g ift=f(t
1
;:::;t
n
)withf 6=e:
Itisextendedtorewritesystemsasfollows:
distr(R)=fl!r 0
jl!r2Risnodistributionrule foreandr 0
2distr(r) g:
A rewrite system is alled right-linear if no right-hand side of arule ontains
multiple ourrenesofthesamevariable.Thefollowingtheoremextends Zan-
tema'ssoundnessresultfordistributionelimination totheACase.
Theorem8. LetR=E bean ETRSwith E =AC(e) suhthat edoesnot our
in the left-handsides of rewrite rules ofR thatarenotdistribution rulesfor e.
If distr(R) isterminatingandright-linear thenR=E isterminating.
Proof. We turn the set of nite non-empty multisets over T(F
distr
;V) into an
F-algebraAbydening
f
A (M
1
;:::;M
n )=
(
ff(t
1
;:::;t
n )jt
i 2M
i
forall16i6ng iff 6=e;
M
1 [M
2
iff =e
for all funtion symbols f 2 F and nite non-empty multisets M
1
;:::;M
n of
terms in T(F
distr
;V). (Notethat n=2if f = e.)We equip Awith the (well-
founded)partial order =
=
mul
where =! +
distr(R)
. Oneeasily shows that
(A;) is amonotone F-algebra. It an be shown (f. the nontrivial proof of
Theorem12in [23℄)that
1. l=
A
rforeverydistributionrule l!r2R,
2. l
A
rforeveryotherrulel!r2R.
e
A
weobtaine(x;y)=
A
e(y;x)and e(e(x;y);z)=
A
e(x;e(y;z)).Hene(A;)
isaquasi-modelofR=E.
Denethe(monotone)labelling`asfollows:`
f
=f
A
forallfuntionsymbols
f 6=e.AordingtoTheorem3itissuÆienttoshowthatR=E
lab
isterminating.
Dene the preedene =on F
lab
asfollows:f =g if and only ifeither f 6= e
andg=eorf =f 0
M
andg=g 0
N
withM(([B) +
)
mul
N.Notethat=iswell
founded.WelaimthatRispreedeneterminatingwithrespetto=.Rewrite
rulesin De areof theform f
M (x
1
;:::;x
n )!f
N (x
1
;:::;x
n
)withM
mul N
and thus f
M
= f
N
. Forrules in R
lab
we make use of the following property,
whihisnotdiÆultto prove:
3. iftCrthen[℄(r)B
mul
[℄(t)foreveryassignment.
Nowletl!r2R
lab
.Bydenition thereisanassignment:V !T(F
distr
;V)
and a rewriterule l 0
!r 0
2 R suh that l=lab
(l
0
) and r =lab
(r
0
). Sine
root(l 0
) 6=e, the label of the root symbolof l is [℄(l 0
). If e ours in r 0
then
root(l) = e by denition. Let M be the label of a funtion symbol in r. By
onstrutionM=[℄(t)forsomesubtermtofr 0
.Wedistinguishtwoases.First
onsidertheasethatl 0
!r 0
2Risadistributionrule.Beauseroot(r 0
)=e,tis
apropersubtermofr 0
.Property(3)yields[℄(r 0
)B
mul
[℄(t).Wehave[℄(l 0
)=
[℄(r 0
)by(1). Hene[℄(l 0
)(([B) +
)
mul
M asrequired.Next letl 0
!r 0
2R
beanon-distribution rule.From(3) we inferthat [℄(r 0
)D
mul
[℄(t) (if t =r 0
then[℄(r 0
)=[℄(t)holds).Aordingto(2)wehave[℄(l 0
)
mul [℄(r
0
).Hene
also in this asewe obtain[℄(l 0
)(([B) +
)
mul
M. This ompletes the proof
ofpreedeneterminationofR .SineE
lab
=E=AC(e), terminationofR=E
lab
followsfrom Lemma1. ut
Nextweshowthat theright-linearityrequirementin thepreeding theorem
an be dropped if terminationis strengthened to total termination. A TRS is
alled totally terminatingifit is ompatible with awell-founded monotoneal-
gebra in whih the underlying order is total. Sine adding a onstant to the
signature does not aet total termination, from now on we assume that the
set ofgroundterms isnon-empty. Totaltermination isequivalent (see[9,The-
orem13℄)toompatibilitywithawell-foundedmonotonetotalorderonground
terms.Here,\ompatibility" meansthat l r holds forallrules l!r2R
and all substitutions suh that l is a ground term. It should be noted that
standardterminationtehniqueslikepolynomialinterpretations,reursivepath
order,and Knuth-Bendixorderallyieldtotaltermination.
Theorem9. LetR=E bean ETRSwith E =AC(e) suhthat edoesnot our
in the left-handsides of rewrite rules ofR thatarenotdistribution rulesfor e.
If distr(R) istotally terminatingthenR=E isterminating.
Proof. There is a well-founded monotone total order on T(F
distr
) whih is
ompatible with distr(R). We turn T(F
distr
) into an F-algebra A bydening
f
A (t
1
;:::;t
n ) =f(t
1
;:::;t
n
)if f 6= eand f
A (t
1
;:::;t
n
)=maxft
1
;t
2
gif f =
1 n distr
the (well-founded) partial order . One an show that (A;) is a monotone
F-algebra. It is not diÆult to verify that l =
A
r for every distribution rule
l!r2Randthetwoequationslr2E.An easyindutionproofshowsthat
1. foralltermsr2T(F;V)andassignmentsthereexistsaterms2distr(r)
suhthat [℄(r)=[℄(s).
Using this property, weobtain (by indution on r)that l
A
r for everynon-
distributionrulel!r2R.Hene(A;)isaquasi-modelofR=E.
Denethe(monotone)labelling`asfollows:`
f
=f
A
forallfuntionsymbols
f 6=e.AordingtoTheorem3itissuÆienttoshowthatR=E
lab
isterminating.
Denethepreedene=onF
lab
asfollows:f =gifandonlyifeitherf 6=eand
g=eorf =f 0
s
andg=g 0
t
withs([B) +
t.Notethat=iswellfounded.The
followingpropertyisnotdiÆulttoprove:
2. iftCrthen[℄(r)D[℄(t)foreveryassignment.
However,[℄(r)B[℄(t) neednot hold (onsidere.g.t Ce(t;t)) andasa on-
sequene the labelled distribution rules in R are not preedene terminating
withrespetto=.Nevertheless,thepreedeneterminationofthelabellednon-
distributionrulesinR
lab
aswellastherulesinDeisobtainedasintheproofof
Theorem8.HeneanyAC-ompatiblereursivepathorder= AC
rpo
induedbythe
preedene=thatisdenedontermswithvariables(f.theproofofLemma1)
will orientthese rulesfrom leftto right.Letl=C[e(x;y)℄!e(C[x℄;C[y℄)=r
beadistributionruleinRandletbeanarbitraryassignment.Welaimthat
lab
(l)=
AC
rpo lab
(r). SineC 6=,root(lab
(l))=e=root(lab
(r))bydeni-
tion.ItsuÆestoshowthatlab
(l)=
AC
rpo lab
(C[x℄)andlab
(l)=
AC
rpo lab
(C[y℄).
Wehave lab
(C[x℄)=C
1 [x℄, lab
(C[y℄)=C
2
[y℄ forsomelabelled ontextsC
1
andC
2
,andlab
(l)=C
1
[e(x;y)℄if(x)(y)andlab
(l)=C
2
[e(x;y)℄other-
wise.Weonsideronlythease(x)(y)here.WehaveC
1
[e(x;y)℄= AC
rpo C
1 [x℄
by the subterm property of = AC
rpo
. If (x) = (y) then C
2
[y℄ = C
1 [y℄ and
thus also C
1
[e(x;y)℄ = AC
rpo C
2
[y℄ by the subterm property. If (x) (y) then
C
1
[e(x;y)℄ = AC
rpo C
2
[y℄ beause the rewrite rule C
1
[e(x;y)℄ ! C
2
[y℄ is pree-
dene terminating. This anbe seen as follows. The label of the root symbol
of C
1
[e(x;y)℄ is [℄(C[x℄). Let q be the label of a funtion symbol in C
2 [y℄.
Byonstrution q =[℄(t) for somesubterm t of C[y℄. We obtain[℄(C[y℄)D
[℄(t)=q from (2). Themonotoniity ofAyields [℄(C[x℄)[℄(C[y℄).Hene
[℄(C[x℄)([B) +
q asdesired.WeonludethatR=E
lab
isterminating.The-
orem3yieldstheterminationofR=E. ut
Theabovetheorem extends asimilar result forTRSs in Zantema [23℄.A-
tually, in [23℄ it is shown that R is totally terminating if distr(R) is totally
terminating. Our semanti labelling proof does not give total termination of
R=E. Nevertheless,themoreompliatedproof in[23℄ anbeextended todeal
withAC(e),soR=E isin fattotallyterminating.
InMiddeldorp et al. [16℄ it is shown that forE = ? theright-linearityre-
quirementinTheorem8anbedroppediftherearenodistribution rulesinR.
thatthesemantilabellingproofin[16℄doesnotextendtoR=E beausethein-
terpretationof edened there,anarbitraryprojetionfuntion,isinonsistent
withtheommutativityofe.
Aknowledgements. We are grateful to the anonymous referees for their areful
reading. Aart Middeldorp is partially supported by the Grant-in-Aid for Sienti
ResearhC(2)11680338oftheMinistryofEduation, Siene,SportsandCultureof
Japan.JurgenGieslissupportedbytheDFGundergrantGI274/4-1 .
Referenes
1. T. Arts and J. Giesl, Termination of Term Rewriting Using DependenyPairs,
TheoretialComputerSiene236,pp.133{178,2000.
2. A.BenCherifaandP.Lesanne,TerminationofRewritingSystemsbyPolynomial
Interpretationsand itsImplementation,SieneofComputerProgramming9(2),
pp.137{159,1987.
3. F. BaaderandT. Nipkow,Term Rewriting andAll That,CambridgeUniversity
Press, 1998.
4. N. Dershowitz, Termination of Rewriting, Journal of Symboli Computation 3,
pp.69{116,1987.
5. N.DershowitzandZ.Manna,ProvingTerminationwithMultisetOrderings,Com-
muniationsoftheACM22(8),pp.465{476,1979.
6. M.C.F. Ferreira, Dummy Elimination in Equational Rewriting, Pro. 7th RTA,
LNCS1103,pp.78{92, 1996.
7. M.C.F. Ferreira, D.Kesner, andL. Puel,Reduing AC-Termination toTermina-
tion,Pro.23rdMFCS,LNCS1450,pp.239{247,1998.
8. M.C.F.FerreiraandH.Zantema,DummyElimination:MakingTerminationEas-
ier,Pro.10thFCT,LNCS965,pp.243{252,1995.
9. M.C.F.FerreiraandH.Zantema,TotalTerminationofTermRewriting,Appliable
AlgebrainEngineering,CommuniationandComputing7,pp.133{162,1996.
10. A.Geser,RelativeTermination,Ph.D.thesis,UniversitatPassau,1990.
11. J.-P.Jouannaud and M. Mu~noz, Termination of aSet ofRules Modulo aSet of
Equations,Pro.7thCADE,LNCS170,pp.175{193,1984.
12. D.KapurandG.Sivakumar,A Total,GroundPathOrderingfor ProvingTermi-
nationofAC-RewriteSystems,Pro.8thRTA,LNCS1232,pp.142{155,1997.
13. D.Kapur,G.Sivakumar,andH.Zhang,ANew MethodforProvingTermination
ofAC-RewriteSystems,Pro.10thFSTTCS,LNCS472,pp.133{148,1990.
14. C.MarheandX.Urbain,TerminationofAssoiative-CommutativeRewritingby
DependenyPairs, Pro.9thRTA,LNCS1379,pp.241{255,1998.
15. A.MiddeldorpandH.Ohsaki,TypeIntrodutionforEquationalRewriting,Ata
Informatia,2000.Toappear.
16. A. Middeldorp, H. Ohsaki, and H.Zantema, TransformingTermination by Self-
Labelling,Pro.13thCADE,LNAI1104, pp.373{387,1996.
17. A.Middeldorp,H.Zantema,SimpleTerminationofRewriteSystems,Theoretial
ComputerSiene175,pp.127{158,1997.
18. M.NakamuraandY.Toyama,OnProvingTerminationbyGeneralDummyElim-
ination, Tehnialreportof IEICE, COMP 98-58 (1998-11), pp. 57{64, 1998. In
Japanese.
1999.
20. A.RubioandR.Nieuwenhuis,ATotalAC-CompatibleOrderingBasedonRPO,
TheoretialComputerSiene142,pp.209{227,1995.
21. J. Steinbah,Termination of Rewriting:Extensions, Comparison and Automati
GenerationofSimpliationOrderings,Ph.D.thesis,Univ.Kaiserslautern,1994.
22. Y.Toyama,CounterexamplestoTerminationfortheDiretSumofTermRewriting
Systems,InformationProessingLetters25,pp.141{143,1987.
23. H.Zantema,TerminationofTermRewriting:InterpretationandTypeElimination,
JournalofSymboliComputation17,pp.23{50,1994.
24. H.Zantema,TerminationofTermRewriting bySemantiLabelling,Fundamenta
Informatiae24,pp.89{105,1995.