Dissertation ETH Zurich No. 27046
Optimality in Distributed Control
from Convex Programming to Reinforcement Learning
A dissertation submitted to attain the degree of Doctor of Sciences of ETH Zurich
(Dr. Sc. ETH Zurich)
presented by
Luca Furieri
M. Sc., Universit` a degli studi di Bologna, Italy born 11.10.1992 in Arezzo
citizen of Italy
accepted on the recommendation of Prof. Dr. Maryam Kamgarpour, examiner Prof. Dr. Antonis Papachristodoulou, co-examiner
Prof. Dr. Giancarlo Ferrari-Trecate, co-examiner
2020
ETH Zurich
IfA - Automatic Control Laboratory ETL, Physikstrasse 3
8092 Zurich, Switzerland c Luca Furieri, 2020 All Rights Reserved ISBN 978-3-907234-43-3
DOI 10.3929/ethz-b-000479163
Ai miei genitori
Acknowledgements
First and foremost, I would like to express my most sincere gratitude to Prof. Maryam Kamgarpour, for choosing me as her Ph.D. student and giving me the opportunity of undertaking a fulfilling and enriching journey under her guidance. I am grateful for the well-balanced mix of close and personalized supervision, especially during the first periods, and freedom to identify and pursue diverse research topics later. You have offered me plentiful of opportunities for professional and personal growth; looking back to four years ago, I genuinely feel proud of having come such a long way, and this is largely thanks to you. I am also thankful for your personal support and useful advice to serenely navigate the more challenging times.
It was an incredible privilege to work together with several outstanding professors and researchers. My deepest thanks go to Prof. Antonis Papachristodoulou for hosting me in Oxford, offering invaluable feedback and advice, and serving as my thesis referee.
His insightful questions and continuous encouragement were key in fully developing the sparsity invariance approach. I specially thank Prof. Giancarlo Ferrari Trecate for the inspiring discussions during conferences and for serving as my other external referee.
It is thanks to Giancarlo’s EECI course in Paris that I first started thinking about sparse Lyapunov functions. My sincere thanks go to Prof. Na Li for working together on controller parametrizations and supporting my grant application. It has been a pleasure to work with Dr. Yang Zheng on many papers; our collaboration has been highly productive and I am thankful for all the insightful brainstorming sessions. I thank Prof.
Elisabetta Tedeschi and Atousa Elahidoost very much for our exchanges and the nice joint works on optimal control for power systems. My thanks extend to Luca Varano for his contribution in developing the numerical simulations for the platooning application.
I also thank Prof. Tyler Summers, Prof. Mihailo Jovanovic, Prof. Claudio De Persis, Prof. Pietro Tesi, Prof. Nikolai Matni, Prof. James Anderson and Prof. John Doyle for all the detailed discussions on exciting research topics.
I am thankful to the other professors at IfA for creating and maintaining an excellent work environment, and for attracting many amazing researchers. I thank Prof. Florian D¨orfler for having me as a teaching assistant in the Advanced Topics for Control course, which has been a really enjoyable and formative experience. I also thank Florian for his valuable feedback on the ECC 2019 presentation and the insightful discussions. I thank Prof. John Lygeros for our collaboration on teaching in Linear System Theory and Prof. Roy Smith for the extremely interesting discussions about control systems,
emerging naturally during each Control Systems 2 teaching meeting.
I would further like to express my gratitude to Prof. Lorenzo Marconi, for first sparking my interest in control theory by allowing me to participate in research projects at the University of Bologna very early on, and for laying solid theoretical foundations that have been essential during my Ph.D. experience. It is thanks to Lorenzo that I had the privilege to conduct my Master Thesis at ETH at the Autonomous Systems Laboratory. Many thanks to Dr. Thomas Stastny, Dr. Igor Gilitschenski and Prof.
Roland Siegwart for guiding me through my work on windy guidance laws for fixed- wing UAVs. It has been an extraordinarily formative, fruitful and fun experience - from crashing a plane on one of the many flowery hillsides in Zurich to winning an award!
I am immensely fortunate for having been part of IfA during these four years, and I would like to thank all of my bright and friendly colleagues. It has been amazing to spend so many memorable and fun moments together!
My gratitude goes to: Or¸cun Karaca, for sharing the vast majority of this Ph.D. jour- ney together, for making every day in the office cheerful, for the enjoyable experience teaching the Linear System Theory course together and for all the support and sugges- tions throughout; Yimeng Lu for all the interesting discussions, for the shared interests and for introducing me to several sport activities; my other office mates Catalin Arghir and Marius Schmitt for all the pleasant memories; Ilnura Usmanova for helping me check a very important proof, the extremely insightful discussions on zeroth-order optimiza- tion, the cakes during group meetings and many enjoyable moments; Pier Giuseppe Sessa, for his helpful and well-thought feedback at each and every meeting, for collabo- rating in teaching Control Systems 2, and for teaching me the side-spin back-hand serve;
Nicol`o Pagan, for the enjoyable times during Linear System Theory, for sharing many SuperKondi sessions and for all the discussions; Andrea Martinelli, for the incredibly great fun at CDC in Miami and ECC in Naples, and for expanding my culinary horizons towards grasshopper tacos and meloncello; Goran Banjac, for the frequent cheerful chats in the corridor and the amusing times at CDC in Nice; Ben Flamm, for organizing many social events, the fun times outside of the lab and inspiring me to recently take up running (next SOLA hopefully); Mohammad Khosravi, for his cheery attitude, for his eagerness to chat about interesting research ideas and for the nice times at ECC in Naples and CDC in Nice; Yvonne St¨urz, for the interesting discussions about distributed control and the fun times at CDC in Nice; Suli Zou and Vasileios Lefkopoulos, for the sightseeing in Pompei; Joe Warrington, Andrea Iannelli, Tony Wood, Sandro Merkli, Jeremy Coulson and Paul Beuchat, for the time at ECC in Naples; Basilio Gentile, for mentoring me dur- ing my first teaching experience; Wenjun Mei for the nice teaching collaboration during Linear System Theory; Samuel Balula for his positive attitude and for organizing the IfA Ping-Pong tournament; Angeliki Kamoutsi, for sharing the IfA coffee talks duties early on, for teaching Linear Systems Theory together and for the support; Ahmed Aboudo-
nia and Lukas Ortmann, for the enjoyable and productive times during Control Systems 2; Mathias Hudoba de Badyn and Menta Sandeep, for starting the Anime club in the Aquarium; and my amazing colleagues Eva Ahbe, Liviu Aolaritei, Georgios Darivianakis, Damian Frick, Adrian Hauwirth, Nicolas Lanzetti, Alexander Liniger, Francesco Micheli, Dario Paccagnan, Anil Parsi, Miguel Picallo Cruz, Bala Kameshwar Poolla, Felix Rey, Irina Subotic, Alexandros Tanzanikis.
Stepping away from Zurich, I would like to thank my friends Francesco D., Francesco B., Raffaele, Cecilia, Giulia, Benedetta, Lorenzo, Margherita, the Bologna gang Fabio, Manuel, Mela and Alessandro, for keeping in touch and finding the time to meet up whenever I visited Italy.
Last, but most definitely not least, I owe my deepest thanks to both of my parents.
It is impossible to acknowledge all the infinite ways in which you have supported me through all these years. It is only thanks to you and your unconditioned and persistent encouragement and trust if I was able to reach this milestone. Thanks for empowering me through the freedom to pursue my path, for always listening and helping find solutions to any issues.
Luca Furieri Zurich, September 2020
Abstract
The recent years have witnessed a steadily increasing deployment of large-scale systems and infrastructures in several cyber-physical domains, ranging for instance from the continent-wide electricity grid to eCommerce platforms. It is expected that in the com- ing years large-scale systems will impact further aspects of our everyday lives: just to name a few examples, from mobility on demand and autonomous guidance to the study of biochemical reaction networks in medicine. One crucial question remains mostly unexplored: how do we optimally and safely operate these systems when their global behaviour depends on the coordination of multiple agents, none of which can observe the overall system?
This thesis intends to focus on the mathematical aspects of the matter presented above. Specifically, the goal of our study is to develop efficient algorithms to synthesize control policies that are optimal and safe. These policies must be based exclusively on measurements that are locally available to each agent; we refer to such control laws as optimal distributed controllers. Motivated by the lack of sufficiently accurate dynamical models for such complex dynamical systems, we additionally wish to investigate how these algorithms can operate without knowing the models. In this sense, we require that they are solely based on the observed data, or as commonly stated in the machine- learning field, that they are data-driven.
In the first part of this thesis, we focus on further refining our understanding of the challenges inherent to using convex programming as a tool for synthesizing globally optimal distributed controllers given a lack of full information. Our main contribution is to reinterpret the classical result of quadratic invariance (QI) to identify more complex decentralization schemes that achieve global optimality. We additionally include robust safety constraints. We finally suggest a new mathematical instrument that allows to parametrize controllers in an input-output way.
In the second part of this thesis we turn our attention to how one can obtain convex approximations in the presence of arbitrary information structures. Our key contribu- tion is a novel method denoted as sparsity invariance (SI) for the synthesis of tight convex restrictions. The main advantages of SI are that i) SI recovers both previous global optimality results given QI and previous heuristics as special cases, ii) SI outper- forms previous methods, as we illustrate through specific examples, and iii) SI is widely adaptable, as it can be naturally encapsulated inside significantly different control frame- works. We study applicability of SI and highlight its benefits on a real-world platooning
scenario.
In the third part of this thesis, we investigate the gradient-descent landscape in order to assess the efficacy of reinforcement learning algorithms when the dynamical model is unknown. The milestone we achieve is to establish sample-complexity bounds to synthesize globally optimal distributed controllers when QI holds. We further show that gradient-descent ensures global optimality for a class of problems that is strictly larger than QI problems. To the best of our knowledge, our works are the first to address global optimality for distributed control in a data-driven setup.
Sommario
Negli ultimi anni abbiamo assistito ad un crescente dispiegamento di sistemi di larga scala ed infrastrutture ciber-fisiche per applicazioni che si estendono, ad esempio, dalla rete elettrica continentale alle piattaforme di eCommerce. Si prevede che nei prossimi anni i sistemi di larga scala avranno impatto su ulteriori aspetti della nostra vita quotidiana:
solo per citarne alcuni, dalla mobilit`a su richiesta, alla guida autonoma e allo studio in medicina di reti di reazioni biochimiche. Una questione cruciale rimane per lo pi`u inesplorata: come possiamo gestire tali sistemi in maniera ottimale e sicura quando il loro comportamento globale dipende dal coordinamento di molteplici agenti, nessuno dei quali pu`o per`o osservare il sistema complessivo?
Questa tesi intende concentrarsi sugli aspetti matematici della questione sopra esposta.
Nello specifico, l’intento del nostro studio `e quello di sviluppare algoritmi efficienti per sintetizzare leggi di controllo ottimali e sicure. Tali leggi devono basarsi esclusivamente su misurazioni che sono disponibili localmente per ogni agente; ci riferiamo a tali leggi di controllo con il termine controllori ottimali distribuiti. Motivati dalla mancanza di modelli dinamici sufficientemente accurati per tali sistemi dinamici complessi, vogliamo in aggiunta investigare come si possa fare in modo che questi algoritmi operino senza conoscere i modelli. In tal senso, richiediamo che essi si basino esclusivamente sui dati osservati, o come si dice comunemente in machine-learning, vogliamo che siano data- driven.
Nella prima parte di questa tesi, ci occupiamo di affinare la comprensione delle difficolt`a insite nell’utilizzo della programmazione convessa come strumento per sin- tetizzare controllori distribuiti globalmente ottimi in mancanza di informazione com- pleta. Il nostro contributo principale consiste nel reinterpretare il risultato classico della quadratica invarianza (QI) per identificare schemi di decentralizzazione pi`u complessi che rendano possibile l’ottimalit`a globale. Includiamo poi vincoli di sicurezza robusta.
Proponiamo infine un nuovo strumento matematico che permette di parametrizzare i controllori in una maniera “input-output”.
Nella seconda parte di questa tesi rivolgiamo la nostra attenzione su come ottenere approssimazioni convesse in presenza di strutture di informazione arbitrarie. Il nostro contributo chiave `e un metodo innovativo denominato invarianza di sparsit`a (SI) per la sintesi di restrizioni convesse molto prossime ad essere esatte. I principali vantaggi della SI sono chei) la SI recupera come sottocasi sia i precedenti risultati di ottimalit`a globale che precedenti approcci euristici,ii) la SI sorpassa in performance i precedenti approcci,
come dimostriamo con esempi specifici, iii) la SI esibisce una ampia adattibilit`a, in quanto pu`o essere naturalmente incapsulata all’interno di scenari di controllo significati- vamente differenti tra di loro. Studiamo anche l’applicabilit`a della SI e ne sottolineiamo i benefici su uno scenario realistico di guida autonoma in formazione.
Nella terza parte di questa tesi, esploriamo il “panorama” della discesa del gradiente al fine di valutare l’efficacia di algoritmi di reinforcement learning quando il modello dinamico `e sconosciuto. Il risultato raggiunto `e quello di stabilire upperbound sulla complessit`a di campionamento per ottenere controllori distribuiti che sono globalmente ottimi quando vale la QI. Dimostriamo inoltre che la discesa del gradiente assicura ot- timalit`a globale per una classe di problemi strettamente pi`u larga dei problemi QI. A nostra conoscenza, i nostri lavori sono i primi a trattare l’ottimalit`a globale per il con- trollo distribuito in un contesto data-driven.
Contents
Acknowledgements i
Abstract v
Sommario vii
Notation xv
1 Overview 1
1.1 Outline and Contributions . . . 2
1.1.1 Part I: parametrizations and global optimality . . . 2
1.1.2 Part II: sparsity invariance . . . 3
1.1.3 Part III: first- and zeroth-order methods . . . 4
1.2 Publications . . . 5
1.2.1 Part I: parametrizations and global optimality . . . 5
1.2.2 Part II: sparsity invariance . . . 6
1.2.3 Part III: reinforcement learning for distributed control . . . 6
1.2.4 Other publications . . . 7
1.3 Code for Numerical Examples . . . 7
I Convex Programming For Robust Distributed Control
Unified Approach to Global Optimality9
2 Introduction 11 2.1 Related Works. . . 123 Preliminaries for Part I and Part II 15 3.1 Preliminaries on Control and Optimization . . . 15
3.1.1 Transfer functions . . . 15
3.1.2 System norms . . . 16
3.2 The Norm-Minimization Problem and LQG . . . 17
3.2.1 State-space formulation. . . 17
3.2.2 The set of stabilizing controllers . . . 18
3.2.3 The norm-minimization problem. . . 19
3.2.4 The LQG problem as a special case and its analytical solution . . 19
3.3 LMI Lyapunov-based Approach for Static Feedback . . . 21
3.4 The Youla Parametrization and Finite-dimensional Approximations . . . 23
3.4.1 Finite-dimensional approximations . . . 24
3.5 Sparse Controller Design . . . 25
3.5.1 Preliminaries on sparsities . . . 25
3.5.2 Quadratic invariance . . . 26
4 Revisiting Youla: The Input-Output Parametrization (IOP) 29 4.1 The Input-Output Parametrization (IOP) . . . 30
4.2 Equivalence with Youla: beyond Doubly-Coprime Factorizations . . . 31
4.3 Quadratic Invariance and the IOP . . . 32
4.4 Implementing the IOP . . . 33
4.4.1 Linear programming for stabilizing controllers . . . 33
4.4.2 Application examples: norm-optimal distributed control . . . 34
4.5 Conclusions . . . 36
4.6 Related Further Work by the Author . . . 37
5 Globally Optimal Robust Distributed Control with Convex Program- ming 41 5.1 The Robust Distributed Control Problem . . . 41
5.2 Convexity For Arbitrary Information Structures . . . 44
5.2.1 Disturbance-feedback parametrization. . . 44
5.2.2 Quadratic invariance for convexity given an arbitrary information structure . . . 46
5.3 The Case of Fixed Sensing and Communication Topologies . . . 50
5.3.1 Sensor information structures . . . 50
5.3.2 Sensor and communication information structures . . . 52
5.4 Conclusions . . . 54
II Sparsity Invariance
Near-Optimal Convex Programming for Arbitrary Sparsities Beyond QI
57
6 Introduction 59
6.1 Related Works. . . 59
7 Sparsity Invariance for Arbitrary Information Structures Beyond QI 63 7.1 Problem Statement . . . 64
7.2 Sparsity Invariance . . . 64
7.2.1 Characterization of SI . . . 66
7.2.2 Optimized design of SI. . . 67
7.3 Beyond Quadratic Invariance . . . 70
7.3.1 Convex restrictions for non-QI sparsity patterns . . . 71
7.3.2 Connections of SI with QI . . . 71
7.3.3 Strictly beyond QI . . . 74
7.3.4 SI for static controller design. . . 75
7.4 Experiments . . . 76
7.4.1 Finite-dimensional approximation . . . 76
7.4.2 Numerical results . . . 77
7.5 Conclusions . . . 78
8 Sparsity Invariance For Separable Lyapunov Functions 81 8.1 Problem Statement . . . 82
8.1.1 Notation on graphs . . . 82
8.1.2 Problem statement . . . 82
8.1.3 A class of convex restrictions. . . 84
8.2 Feasible Convex Restrictions Based on Separable Lyapunov Functions . . 84
8.2.1 Sparsity invariance for convex restrictions . . . 84
8.2.2 Separable Lyapunov functions for feasible convex restrictions . . . 86
8.3 Optimized Lyapunov Sparsities . . . 88
8.4 Network Example . . . 90
8.5 Conclusions . . . 92
9 Sparsity Invariance for Robust Distributed Control 95 9.1 Problem Formulation . . . 95
9.2 Generalized Sparsity Subspaces . . . 97
9.3 Upper Bounds Beyond Quadratic Invariance . . . 100
9.4 Conclusions . . . 101
10 Sparsity Invariance in Practice: The Case of Platooning 103 10.1 The Platooning Problem as Distributed LQG . . . 104
10.2 QI and SI for Platooning . . . 107
10.2.1 QI platooning information structures . . . 107
10.2.2 SI for deployable non-QI platooning information structures . . . . 109
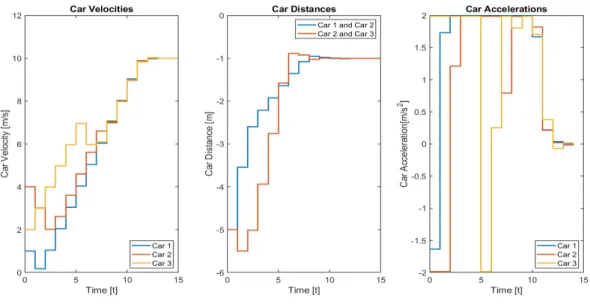
10.3 Numerical Results. . . 110
10.4 Conclusions . . . 112
III Reinforcement Learning For Distributed Control
Global Optimality with First- and Zeroth-order Methods115
11 Introduction 117 11.1 Related Works. . . 11811.1.1 First-order methods for centralized control . . . 118
11.1.2 Data-driven control . . . 118
11.1.3 Learning distributed controllers . . . 119
12 Preliminaries for Part III 121 13 Global Convergence of Gradient-descent for Distributed Control 127 13.1 Preliminaries on QI and Gradient Descent . . . 127
13.1.1 Problem formulation and remarks . . . 128
13.1.2 Strong quadratic invariance . . . 128
13.2 First-order Methods for Globally Optimal Distributed Controllers given QI129 13.2.1 Global optimality of gradient-descent . . . 130
13.2.2 Numerical example . . . 132
13.3 Unique Stationarity: Global Optimality Beyond QI . . . 133
13.3.1 Unique stationarity generalizes QI . . . 134
13.3.2 Tests for unique stationarity . . . 136
13.4 Conclusions . . . 137
14 Reinforcement Learning for Distributed Control 139 14.1 Problem Formulation . . . 139
14.2 Local Gradient Dominance for QI Problems and Beyond . . . 141
14.3 Learning the Globally Optimal Constrained Control Policy . . . 143
14.3.1 Sample-complexity bounds . . . 144
14.3.2 Experiments for distributed control . . . 146
14.4 Conclusions . . . 147
IV Conclusions 155
15 Conclusions and outlook 157 15.1 Part I: Parametrizations and Global Optimality . . . 15715.1.1 Further research directions . . . 157
15.2 Part II: Sparsity Invariance . . . 158
15.2.1 Further research directions . . . 158
15.3 Part III: First- and Zeroth-order Methods . . . 159
15.3.1 Further research directions . . . 160
Notation
Acronyms
GSS generalized sparsity subspace IOP input-output parametrization LMI linear matrix inequality
LP linear program
LQ linear quadratic
LQG linear quadratic gaussian LQR linear quadratic regulator LTI linear time-invariant
PN partially nested/partial nestedness
QI quadratic invariance/quadratically invariant QP quadratic program
SDP semi-definite program SI sparsity invariance US uniquely stationary
Standard symbols
:= equal by definition
N, N[a,b] set of natural numbers, set of x∈N such thata≤x≤b
R set of real numbers
[a, b] interval ofx∈R such that a≤x≤b
C set of complex numbers
<(z) real part of z ∈C
e.g. x and A vectors and matrices, respectively
vec(A)∈Rmn vector stacking the columns of A∈Rm×n into a single vector
vec−1(a)∈Rm×n matrix whose n columns are consecutive sub-vectors in Rm of vector a∈Rmn 0m×n m×n matrix with all entries equal to zero
1m×n m×n matrix with all entries equal to one In identity matrix In∈Rn×n
ei ∈Rn i−th element of the standard orthonormal basis for Rn
A0 (0) positive definite (resp. semi-) A∈Rn×n, i.e., x>Ax >0 (resp ≥0), ∀x6= 0 kxk2 2-norm of x∈Rn, kxk2 :=√
xTx
kAkF Frobenius norm of matrix A∈Rm×n,kAkF :=p
Trace(ATA) xi element in position i of the vector x∈Rn
Ai,j orAij element in position (i, j) of the matrix A ∈Rm×n A⊗B Kronecker product of the matrices A, B
AB Hadamard product of the matrices A, B, (AB)i,j := Ai,jBi,j
x∼ D random variable x∈Rn distributed according to a probability distributionD E[x] expected value of random variable x∈Rn
Sr⊆Rd shell of a sphere in Rd of radius r >0
N(µ,Σ) normal distribution with expected value µ∈Rn, variance Σ∈Rn×n s.t. Σ0 ΠX(A) orthogonal projection of A ∈Rm×n ontoX ⊆ Rm×n
∇f(x)∈Rm×n Jacobian of differentiable f :Rm →Rn,i.e.,∇f(x)i,j := ∂f∂xj(x)
i
∇J(A)∈Rm×n gradient of differentiable J :Rm×n→R, i.e., ∇J(A)i,j := ∂J∂A(A)
i,j
∇2f(x)∈Rn×n Hessian of twice differentiable f :Rn →R,∇2f(x)i,j = ∂x∂2f(x)
i∂xj
K⊥⊆Rm×n orthogonal complement of subspace K ⊆Rm×n
Im(A) range of the linear operator associated with A∈Rm×n Ker(A) kernel of the linear operator associated with A∈Rm×n
Symbols for transfer matrices
Rm×nc set of m×n causal transfer matrices
Rm×nsc set of m×n strictly causal transfer matrices RHm×n∞ set of m×n causal and stable transfer matrices
1
zRHm×n∞ set of m×n strictly causal and stable transfer matrices
e.g. xand G signals and transfer matrices, respectively, in the frequency domain kGkH∞ H∞ norm ofG∈ RHm×n∞ , see def. in (3.1)
kGkH2 H2 norm of G∈ 1zRHm×n∞ , see def. in (3.2)
Symbols for binary matrices and sparsity patterns
{0,1}m×n set ofm×n binary matrices
Sparse(X) subspace of transfer matrices with sparsity X ∈ {0,1}m×n, see def. in (3.22) Struct(G) binary matrix encoding the sparsity ofG∈ Rm×nc , see def. in (3.23)
kXk0 cardinality of X ∈ {0,1}m×n, kXk0 := Pm i=1
Pn j=1Xij
Selected reserved symbols
xk vector of system states at time k ∈N
uk vector of inputs to the system at time k ∈N yk vector of measurement outputs at time k∈N zk (Part I & Part II) vector of performance signals at time k∈N ξk vector of internal controller states at time k∈N wk vector of process noise at time k ∈N
vk vector of measurement noise at time k ∈N
n dimension of xk
m dimension of uk
p dimension of yk
Cstab set of stabilizing controllers
K dynamic controller
K static controller
Q Youla parameter
P, P22 open-loop plant, open-loop input-output response f(K) (Part I & Part II) closed-loop map from w toz
f(z) (Part III) cost as a function of equivalent vectorial decision variable J(K) cost as a function of the controller
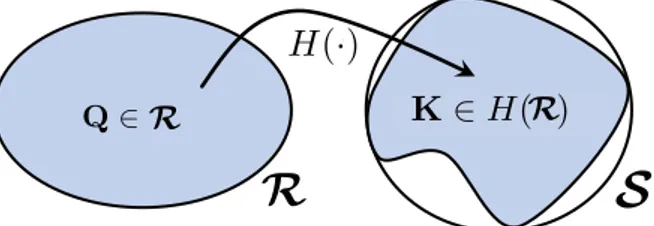
H(·) closed-loop operator over matrix decision variable
h(·) (Part III) closed-loop operator over equivalent vectorial decision variable
CHAPTER 1
Overview
A rising need in modern societies is to safely and efficiently operate several critical large-scale dynamical systems, ranging from the smart grid to biological networks and automated highways; see, for instance, the applications of [D¨or+14; PP14; Zhe+17].
The overall behavior of all these systems is affected by multiple myopic decision-makers in a remarkably intricate way.
CHALLENGE IN COMMON
Communication network
Decentralized controller
Local measurements Micro grid unit
Sys. 1 Dynamical couplings Sys. 2
Decision
Maker 1 Decision
Maker 2
? ?
Figure 1.1: Power grids integrating different sources of renewable energy and platoons of autonomous vehicles are two examples of large-scale dynamical systems. These systems involve multiple decision-makers and are decentralized by nature1.
More specifically, the main challenge in distributed control stems from the presence of multiple decision-making entities. Each of these decision-makers is only able to base its control policy on a small subset of the overall system-wide sensor measurements. This lack of information is typically due to physical distance, privacy concerns or cost-related considerations. Given such inherent limitations and constraints, it is well-known that the corresponding optimal control problems are NP-hard in general [PT86; BT00; Wit68].
In other words, they are not solvable with standard computers in a reasonable time
1Credits for the images and background tohttps://www.flaticon.com/authors/freepik,https:
//www.freepik.com and [PCS19].
even for simple cases. Furthermore, the sheer complexity of critical emerging large-scale dynamical systems leads to a lack of reliable mathematical models to be exploited for control, thus advocating for developing a theory of distributed, learning-based control of dynamical systems.
The goal of this thesis is to address the challenges outlined above:
(a) First, we wish to provide a unified framework for the convex design of distributed controllers that i) are globally optimal and ii) robustly comply with safety con- straints. While providing novel insight and design tools, we note that this goal can only be achieved if a condition known as quadratic invariance (QI) holds.
(b) Second, we aim to go beyond the QI limitations by proposing a generalized convex approach based on a novel notion of sparsity invariance (SI). Our method shall recover QI as a subcase, and outperform previous heuristic approaches.
(c) Third, we want to shift our perspective away from convex optimization towards reinforcement learning algorithms. While investigating fundamental properties of distributed control within a gradient-descent landscape, our goal is to establish the first convergence and sample-complexity results on learning globally optimal distributed controllers.
1.1 Outline and Contributions
1.1.1 Part I: parametrizations and global optimality
In the first part of the thesis we address controller parametrizations and convex pro- gramming techniques for distributed control. We wish to interpret and generalize the conditions needed to synthesize globally optimal controllers in a tractable way, while including safety constraints. We also investigate convex parametrizations of stabilizing controllers beyond the classical Youla parametrization.
Outline. Chapter 2 provides an introduction and an historical overview on opti- mization for distributed control. In Chapter 3 we review preliminary notions on system stability and optimal control formulations in infinite-horizon. We introduce the classical Youla parametrizations of stabilizing controllers, a fundamental tool to design optimal controllers in a convex way. We last define the notion of quadratic invariance (QI) for convexity of distributed control problems. InChapter 4 we suggest a novel parametriza- tion denoted as the input-output parametrization (IOP). We establish its connections with Youla and discuss potential advantages. In Chapter 5 we address the task of de- signing globally optimal distributed controllers that are robustly safe. Furthermore, we provide a unified and generalized understanding of quadratic invariance in finite-horizon.
Contributions. The main contributions of Part I of the thesis are contained in Chapter 4 and Chapter 5, and are detailed as follows.
(a) In Chapter 4 we propose a novel input-output parametrization of the set of in- ternally stabilizing output-feedback controllers for linear time-invariant (LTI) sys- tems. The IOP is designed to avoid the steps of pre-computing a doubly-coprime factorization of the system or an initial stabilizing controller, as required per the Youla and coordinate-free parametrizations. Instead, within the IOP a stabilizing controller is computed by directly solving a linear program (LP). Furthermore, we show that the proposed input-output parametrization allows to compute norm- optimal controllers subject to quadratically invariant (QI) constraints using convex programming.
(b) InChapter 5we unify and generalize the class of systems and information structures for which convexity of the robust distributed control problem in finite-horizon can be certified by finitely many algebraic conditions equivalent to QI. The focus is on deriving the main results of related works as particular cases of the proposed general setup, and characterizing new information structures for which optimal controller synthesis is a tractable problem. Furthermore, we show that polytopic safety constraints on the state and input trajectories can be included in a natural way.
1.1.2 Part II: sparsity invariance
In the second part of the thesis we address optimal and near-optimal sparse controller design given arbitrary information structures. Specifically, we focus on the class of problems that are not QI. To this end, we propose a new notion of sparsity invariance (SI) that allows to develop convex approximations of this generally NP-hard problem that are as tight as possible. The SI notion naturally applies to synthesizing dynamic controllers and static controllers, and it can be encapsulated within the Youla, IOP, SLP or LMI-based parametrizations.
Outline. Chapter 6 introduces the notion of SI as a condition over binary matrices that allows to synthesize sparse controllers. We also review related works. In Chapter 7 we show how the notion SI steps beyond that of QI in several ways that are discussed in detail. Chapter 8 studies the problem of synthesizing static distributed controllers and interprets the notion of SI in terms of designing minimally separable quadratic Lyapunov functions for the closed-loop system. InChapter 9we show that SI can be used to comply with arbitrary spatio-temporal constraints consisting of both sparsity and delays. We validate our results by applying the SI approach to the case of controlling a platoon of autonomous vehicles in Chapter 10.
Contributions. The main contributions of Part II of the thesis are contained in Chapter 7,Chapter 8, Chapter 9, and Chapter 10 and are detailed as follows.
(a) InChapter 7we show that the SI approach offers a direct generalization of previous dynamic controller design methods based on the notion of QI. Specifically, we prove that 1) SI can be directly applied to any systems and sparsity constraints, 2) the recovered solution is globally optimal when QI holds and performs at least as well as the nearest QI subset when QI does not hold, and 3) SI strictly outperforms previous approximations on specific examples.
(b) In Chapter 8 we exploit SI to characterize a novel class of feasible convex restric- tions of the static optimal distributed control problem. We provide necessary and sufficient conditions for the feasibility of these convex restrictions in terms of exis- tence of a corresponding separable Lyapunov function for the closed-loop system.
We show that our approach outperforms previous heuristics.
(c) In Chapter 9 we show that the notion of SI can be applied to arbitrary spatio- temporal constraints in finite-horizon, while complying with safety constraints. In doing so, we define a closely related notion of Generalized Sparsity Subspaces (GSS) approach and discuss its connections with SI.
(d) In Chapter 10 we consider optimal control of a platoon of vehicles complying with hard safety constraints. We first unravel the role played by QI in determining convexity for this problem and we interpret the resulting practical limitations. We then show through simulations that the proposed SI approach recovers near-optimal dynamic controllers that comply with a realistic non-QIpredecessor-follower infor- mation structure.
1.1.3 Part III: first- and zeroth-order methods
In the third part of the thesis we study the properties of the optimal distributed control problem within a reinforcement learning landscape. Our goal is twofold. First, we want to study conditions for convergence of gradient-descent algorithms to globally optimal distributed controllers. We expect such conditions to be less stringent than QI, because QI is a limitation inherent to using convex programming. Second, we turn our attention to establishing sample-complexity bounds of reinforcement learning algorithms to learn globally optimal distributed controllers for unknown dynamical systems.
Outline. Chapter 11provides a literature review of gradient-descent and data-driven methods for control and distributed control. Chapter 12 states important preliminaries on the distributed LQ problem in finite-horizon. In Chapter 13 we study the proper- ties of projected gradient-descent methods as applied to the optimal distributed control problem. Our focus is to characterize conditions for convergence to a global optimum
and study the connections with QI. In Chapter 14 we draw a novel connection between gradient dominance of the cost function and QI, which leads to establishing the first sample-complexity bounds on learning globally optimal distributed controllers using re- inforcement learning.
Contributions. The main contributions of Part III of the thesis are contained in Chapter 13 and Chapter 14, and are detailed as follows.
(a) InChapter 13we first show that if QI holds, a projected gradient-descent algorithm is guaranteed to converge to the global optimum. We then characterize a class of uniquely stationary (US) problems, for which projected gradient descent converges to a global optimum. Furthermore, we show that the class of US problems isstrictly larger than the class of QI problems.
(b) In Chapter 14we provide a framework to learn distributed dynamic linear policies in finite-horizon, without knowing the dynamical model and subject to uncertain initial state, process noise and noisy output observations. Our key contribution is to establish a property of local gradient dominance for a class of distributed control problems that includes 1) all QI problems and 2) some non-QI problems. This local gradient dominance property is crucial to establishing sample-complexity bounds of zeroth-order gradient-descent learning algorithms.
1.2 Publications
This thesis contains a selected collection of the results derived during the author’s studies as a Ph.D. candidate, all of which have already been accepted for publication. The corresponding articles on which this thesis is based are listed below.
1.2.1 Part I: parametrizations and global optimality
The input-output parametrization in Chapter 4 and its equivalence with the Youla parametrization were developed in collaboration with Y. Zheng, A. Papachristodoulou and M. Kamgarpour. The results of Chapter 5 about generalizing and unifying the class of robust distributed control problems solvable through convex programming were developed with the help of M. Kamgarpour.
L. Furieri, Y. Zheng, A. Papachristodoulou, and M. Kamgarpour. “An Input–Output parametrization of stabilizing controllers: amidst Youla and system level synthesis”. In:
IEEE Control Systems Letters 3.4 (2019), pp. 1014–1019
L. Furieri and M. Kamgarpour. “Robust control of constrained systems given an information structure”. In: IEEE Conference on Decision and Control (CDC). 2017,
pp. 3481–3486
L. Furieri and M. Kamgarpour. “Unified approach to convex robust distributed control given arbitrary information structures”. In: IEEE Transactions on Automatic Control 64.12 (2019), pp. 5199–5206
1.2.2 Part II: sparsity invariance
The sparsity invariance approach inChapter 7andChapter 8was developed in collabora- tion with Y. Zheng, A. Papachristodoulou and M. Kamgarpour. The idea of generalized sparsity subspaces in Chapter 9 for robust distributed control was developed with the help of M. Kamgarpour. The numerical results for platooning in Chapter 10 were de- veloped by L. Varano in the context of his Semester Thesis [VD12] at ETH under the direct supervision of the author and M. Kamgarpour.
L. Furieri, Y. Zheng, A. Papachristodoulou, and M. Kamgarpour. “Sparsity invari- ance for convex design of distributed controllers”. In: IEEE Transactions on Control of Network Systems, early access (2020)
L. Furieri, Y. Zheng, A. Papachristodoulou, and M. Kamgarpour. “On separable quadratic Lyapunov functions for convex design of distributed controllers”. In: IEEE European Control Conference (ECC). 2019, pp. 42–49
L. Furieri and M. Kamgarpour. “Robust distributed control beyond quadratic in- variance”. In: IEEE Conference on Decision and Control (CDC). 2018, pp. 3728–3733
1.2.3 Part III: reinforcement learning for distributed control
The convergence analysis of gradient-descent methods for distributed control beyond quadratic invariance was developed in collaboration with M. Kamgarpour. The local gradient dominance property and sample-complexity bounds were developed in collabo- ration with Y. Zheng and M. Kamgarpour.
L. Furieri and M. Kamgarpour. “First order methods for globally optimal dis- tributed controllers beyond quadratic invariance”. In: IEEE American Control Con- ference (ACC). 2020, pp. 4588–4593
L. Furieri, Z. Yang, and M. Kamgarpour. “Learning the Globally Optimal Dis- tributed LQ Regulator”. In: Conference on Learning for Dynamics and Control (L4DC).
vol. 120. Proceedings of Machine Learning Research (PMLR). 2020, pp. 287–297
1.2.4 Other publications
The following papers were published by the author during his doctoral studies, but are not included in this thesis. The main results of [Zhe+20] and [Zhe+19],i.e. the last two references listed below, are mentioned for discussion in Part I, but not treated in detail.
A. Elahidoost, L. Furieri, E. Tedeschi, and M. Kamgarpour. “Optimizing HVDC grid expansion and control for enhancing DC stability”. In: IEEE Power Systems Com- putation Conference (PSCC). 2018, pp. 1–7
A. Elahidoost, L. Furieri, E. Tedeschi, and M. Kamgarpour. “Reducing HVDC Network Oscillations Considering Wind Intermittency Through Optimized Grid Expan- sion Decision”. In: IEEE Energy Conversion Congress and Exposition (ECCE). 2018, pp. 2683–2690
Y. Zheng, L. Furieri, A. Papachristodoulou, N. Li, and M. Kamgarpour. “On the equivalence of Youla, System-level and Input-output parameterizations”. In: IEEE Transactions on Automatic Control (2020)
Y. Zheng, L. Furieri, M. Kamgarpour, and N. Li. “System-level, Input-output and New Parameterizations of Stabilizing Controllers, and Their Numerical Computation”.
In: arXiv preprint arXiv 1909.12346 (2019)
1.3 Code for Numerical Examples
The code for all numerical examples included in this thesis is available at the following locations:
• Examples of Chapter 4 about the input-output parametrization, associated with the paper [Fur+19a]:
https://github.com/furieriluca/Sparsity-Invariance/tree/master/LCSS_
Input-Output
• Examples ofChapter 7about sparsity invariance, associated with the paper [Fur+20]:
https://github.com/furieriluca/Sparsity-Invariance
• Examples of Chapter 8 about separable Lyapunov functions, associated with the paper [Fur+19b]:
https://github.com/furieriluca/Separable-Lyapunov
• Examples of Chapter 10 about platooning, associated with the thesis [Var20]:
https://polybox.ethz.ch/index.php/s/GKWtss95wq6glWk?path=%2FCode%2FFurieri
• Examples of Chapter 13 about first-order methods, associated with the paper [FK20]:
https://github.com/furieriluca/Gradient-Descent-Beyond-QI
• Example ofChapter 14about learning distributed controllers, associated with the paper [FYK20]:
https://github.com/furieriluca/Learning-Controllers-Given-QI
Part I
Convex Programming For Robust Distributed Control
Unified Approach to Global Optimality
CHAPTER 2
Introduction
In this first part of the thesis, we wish to investigate the core challenges and limitations inherent to computing optimal distributed controllers through convex programming.
Our study is motivated by critical emerging large-scale systems, such as the electric power grid, autonomous vehicles, the internet and financial systems, that all feature autonomous and interacting decision making agents. Due to geographic distance or privacy concerns, the agents can only base their decisions on local partial information, and this lack of full information has a significant impact on the design of optimal de- cisions. Specifically, it is well-known that the design of optimal control policies given an information structure can be extremely challenging even in seemingly simple cases [Wit68]. Indeed, the optimal feedback control policies may not even be linear for the LQG problem with decentralized information, and several instances of related problems were formally shown to amount to intractable numerical programs [BT00; PT86]. One main core challenge of decentralized and distributed control can be visualized as per Figure 2.1. InFigure 2.1, the control actions of Decision-Maker 1, represented by a blue
CHALLENGE IN COMMON
Communication network
Decentralized controller
Local measurements Micro grid unit
Sys. 1 Dynamical couplings Sys. 2
Decision
Maker 1 Decision
Maker 2
? ?
Figure 2.1
arrow, affect the observations of Decision-Maker 2, represented by a green arrow, and vice-versa, but the decisions of both are based solely on local information. Therefore, the computation of optimal decisions involves inverting the system dynamics to infer the other decision-maker’s past observations. Such dynamical inversion is nonlinear in
the decision variables, and this makes the optimization intractable from a computational point of view.
2.1 Related Works
Significant work has been directed towards identifying special cases of the optimal dis- tributed control problem for which efficient algorithms can be derived. The work in [HK72] showed that when the information structure is partially nested (PN) the linear quadratic Gaussian (LQG) control problem can be reduced to a static problem, whose optimal solution is linear. More recently, the work [Vou01] established convexity of the problem of optimal disturbance rejection in broader classes of controlled systems, such as those being “nested, chained, hierarchical, delayed interaction and communication, or symmetric” [Vou01]. In [BV05], optimal distributed controller design for spatially invariant systems was shown to be convex given “funnel causality” of the information structure.
The cases [HK72; Vou01; BV05] were unified in the classical works [Rot05; RL06;
Rot08; LL11], where the authors established necessary and sufficient conditions on the plant and the information structure for convexity of optimal control referred to as quadratic invariance (QI). Furthermore, QI was shown to be equivalent to PN for all problems where PN is well-defined [Rot08], therefore proving that, given QI, linear dynamic controllers achieve global optimality. Quadratic invariance, however, revealed a fundamental limitation: full sensor information is needed when all the states dynamically influence each other. Such limitation encouraged including a communication network in the control architecture to restore convexity. Accordingly [RCL10] considered a time- invariant communication network to share local output measurements with fixed delays.
The authors of [RCL10] used the concepts of propagation and transmission delays to derive algebraic conditions that are equivalent to QI for these information structures.
Alternatively, the system level approach [WMD19] has proposed an implementa- tion where controllers are required to share locally estimated disturbances in the state- feedback case and internal controller states in the output-feedback case. We note that the classical distributed control only requires to utilize locally acquired output mea- surements, and not to share any intermediate computations among subsystems. The need to share this additional information and thus violate controller sparsity constraints might raise concerns of system security and vulnerability in safety critical applications [SHG+12], where each subsystem can only rely on its own sensor measurements. We note that a looser notion of structured-realizability of the controller was recently proposed in [JB20], generalizing the concepts of sparse controller and system level implementation.
Given the importance of sparse output-feedback controller synthesis in safety-critical real-life applications such as power systems and platooning, this thesis will solely focus
on synthesizing sparse output-feedback controllers.
Once a convex problem is obtained under the QI condition, one possible approach is to compute optimal controllers in the form of transfer functions by approximating the corresponding infinite-dimensional convex optimization problem [AR13]. Operations at the transfer function level can be numerically unstable [SP13] and may not offer insight into the controllers’ internal dynamics.
Another approach is to explicitly compute distributed optimal controllers within state space representations by using dynamic programming. This approach led to several works, each addressing a specific class of dynamical systems and information structures as follows. The authors in [SP13] considered the case of poset-causal systems given that controllers can only access partial sensor measurements and showed that the problem reduces to a set of decoupled centralized problems. The case of output sharing between controllers with one-timestep delays was analytically solved in [KS74; SA74; Yos75].
Combining sparse sensor measurements and fixed delays in the communication between controllers was considered in [LL15]. In [MLD14], the authors solved the more general case of time-varying delays given a special class of systems consisting of two intercon- nected plants.
In several control scenarios of practical interest, it is important to ensure that states and control inputs remain inside specified safety sets at all times. However, the works mentioned above based on convex programming [Vou01;BV05;Rot05;RL06;Rot08] and on explicit dynamic programming [SP13; KS74; SA74; Yos75; LL15; MLD14] did not address safety constraints. A technique to easily include state and input constraints is distributed model predictive control [Con+16; GR14]. Typically, this approach involves dividing a large-scale system into subsystems that communicate in order to minimize a given cost function, while being robust to the dynamical couplings. Convexity of the resulting optimization problems is obtained at the cost of potential conservativeness by optimizing overopen-loop control vectors instead of closed-loop control policies. Repeat- ing the optimization at every time step mitigates this suboptimality. However, closed- loop control policies have been known to allow for longer prediction horizons without running into infeasibility [Bem98].
The literature review above reveals that, when distributed control is considered, different instances of dynamical systems [Vou01; SP13], time-invariant and time-varying information structures [SP13; KS74; SA74; Yos75; LL15; MLD14], and the inclusion of state and input constraints [Con+16; GR14; Bem98; FK17] are treated as separate challenges, to be addressed with a variety of different approaches and mathematical tools.
To summarize, the goalof Part I is threefold:
1) In Chapter 3 we review the background on convex programming and optimal dis- tributed control necessary for Part I and Part II of this thesis.
2) In Chapter 4 we propose a novel input-output convex parametrization of stabi- lizing controllers alternative to the classical Youla parametrization. We aim to discuss potential advantages of the proposed parametrization and its applicability to distributed control.
3) In Chapter 5 we propose a unified understanding and approach to convex pro- gramming for globally optimal distributed control in finite-horizon. The goal is to characterize new information structures that are QI and to include safety con- straints.
CHAPTER 3
Preliminaries for Part I and Part II
In this chapter we introduce the background required for the development of the first two parts of this thesis. We begin by defining the standard H2 norm minimization problem as an infinite-dimensional non-convex problem. We then consider the linear quadratic Gaussian (LQG) problem as a special instance of H2 norm minimization and present its standard analytical solution based on dynamical programming. Motivated by the limitations of this analytical approach when hard constraints on the control policy are present, we proceed with casting an equivalent finite-dimensional convex-program based on linear matrix inequalities (LMI) and quadratic Lyapunov functions that is valid for the state-feedback case. For the more general output-feedback case, we illustrate how one can cast an infinite-dimensional convex program based on the Youla parametrization.
We further discuss finite-dimensional approximations for this program. We conclude by reviewing the fundamental notion of quadratic invariance (QI) for synthesizing globally optimal sparse controllers. The material presented in this chapter is entirely available in the literature, and we redirect the reader to [Ber+95], [Boy+94], [DY13] and [RL06] for a comprehensive treatment.
3.1 Preliminaries on Control and Optimization
In this section we review concepts related to transfer functions and system norms. We explicitly define system norms for discrete time transfer matrices, as discrete time systems are the main focus of this thesis. We remark that similar definitions exist also for continuous time systems.
3.1.1 Transfer functions
We denote the imaginary axis as jR := {z ∈ C | <(z) = 0} and the unitary circle as ejR :={z ∈C| kzk2 = 1}. A continuous time transfer function is a functionfc:jR→C and a discrete time transfer function is a function fd : ejR → C. A m × n transfer matrix is the set of m ×n matrices whose entries are transfer functions. We denote
the set of m×n causal transfer matrices as Rm×nc , i.e., such that their output in the time domain depends on the present and past inputs. Similarly, we denote the set of m×n strictly causal transfer matrices as Rm×nsc , i.e., such that their output in the time domain depends only on the past inputs. A transfer function is called proper (resp.
strictly-proper) if it is a rational function and the degree of the numerator polynomial does not exceed (resp. is strictly lower than) the degree of the denominator polynomial.
We letRHm×n∞ ⊆ Rm×nc be the set of m×n causal and stable transfer matrices. When dealing with linear systems, RHm×n∞ coincides with the set of m×n proper and stable transfer matrices. We let 1zRHm×n∞ ⊆ Rm×nsc be the set of m×n strictly causal and stable transfer matrices. When dealing with linear systems, 1zRHm×n∞ coincides with the set of m×n strictly proper and stable transfer matrices. Throughout the thesis we sometimes omit the dimension of transfer matrices to ease the reading. The dimensions shall be clear in the context.
3.1.2 System norms
GivenG∈ RH∞, we denote its H∞ norm by
kGkH∞ :=
s
∃ks.t.maxuk6=0
P∞ k=0ykTyk
P∞
k=0uTkuk = sup
ω
σmax(G(ejω)), (3.1)
whereyk and uk denote the output and input vectors at time k respectively andσmax(·) denotes the maximum singular value. In other words, the H∞ norm indicates the max- imum amplification of the input energy to the outputs, and it is an extension of the matrix induced 2-norm to signals. Given a transfer matrix G ∈ 1zRH∞, the square of itsH2 norm is defined as
kGk2H2 :=
X∞ k=0
kG(k)k2F = 1 2π
Z π
−π
Trace G∗(ejω)G(ejω)
dω , (3.2)
where the matrix G(k) denotes the impulse response of the system at time k relating each input to each output, and the equivalence between the infinite-sum in time domain and the definite integral in frequency domain holds due to Parseval’s Theorem. We can also interpret kGkH2 as the expected root mean square (RMS) value of the output in response to unit-intensity white noise input excitation.
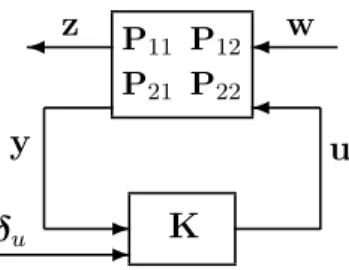
-
y u
w z
K P11 P12 P21 P22
-
δu
Figure 3.1: Interconnection of the plant Pand controller K
3.2 The Norm-Minimization Problem and LQG
3.2.1 State-space formulation
We consider discrete time LTI systems of the form xk+1 =Axk+B1wk+B2uk,
zk =C1xk+D11wk+D12uk, yk =C2xk+D21wk+D22uk,
(3.3)
where xk, uk, wk, yk, zk are the state vector, control action, external disturbance, mea- surement, and performance signal at time k, respectively. System (3.3) can be written as
P=
A B1 B2 C1 D11 D12 C2 D21 D22
=
P11 P12
P21 P22
,
where Pij =Ci(zI−A)−1Bj+Dij. We refer to P as the open-loop plant model. Now consider a dynamic output feedback controller u = Ky+δu, where δu denotes generic disturbance on the input in the frequency domain, and K has a state-space realization
ξk+1 =Acξk+Bcyk,
uk=Ccξk+Dcyk, (3.4)
where ξ is the internal state of controller K. We have K = Cc(zI −Ac)−1Bc+Dc. Figure 3.1 shows a schematic diagram of the interconnection of plant P and controller K. When dealing with infinite-horizon control problems throughout this thesis, we make the following standard assumptions.
Assumption 1. Both the plant and controller realizations are stabilizable and detectable, i.e., (A, B2) and (Ac, Bc) are stabilizable, and (A, C2) and (Ac, Cc) are detectable.
Assumption 2. The interconnection in Figure 3.1 is well-posed, i.e., I − D22Dc is invertible.
3.2.2 The set of stabilizing controllers
We now introduce the definition of external and internal stability of the system inFig- ure 3.1. This overview is based on our work [Zhe+19], but we note that the results are well-known in the literature, see for example [Fra87] and [ZDG96].
Combining (3.3) with (3.4), and defining δx = B1w and δy = D21w, we can write the closed-loop responses from (δx,δy,δu) to (x,y,u) as
x y u
=
Φxx Φxy Φxu Φyx Φyy Φyu Φux Φuy Φuu
δx δy δu
,
where we have Φxx = (zI−A−B2KC2)−1 and
Φxy =ΦxxB2K, Φxu=ΦxxB2,
Φyx=C2Φxx, Φyy =C2ΦxxB2K+I, Φyu =C2ΦxxB2, Φux=KC2Φxx,
Φuy =K(C2ΦxxB2K+I), Φuu=KC2ΦxxB2 +I.
We define the closed-loop response transfer matrix as Φ:=
Φxx Φxy Φxu Φyx Φyy Φyu Φux Φuy Φuu
. (3.5)
The notion of external transfer matrix stability is defined as follows.
Definition 1 ([ZDG96, Chapter 5]). The closed-loop system is externally stable if the closed-loop responses from (δx,δy,δu) to (x,y,u) are all stable, i.e., Φ∈ RH∞.
Internal stability is defined as follows [ZDG96, Chapter 5.3]:
Definition 2. The system in Figure 3.1 is internally stable if it is well-posed, and the states (xk, ξk) converge to zero as k → ∞ for all initial states (x0, ξ0) when wk = 0, ∀k.
We say that the controllerKinternally stabilizes the plantP22 if the closed-loop sys- tem inFigure 3.1 is internally stable. The set of all LTI internally stabilizing controllers is correspondingly defined as
Cstab :={K|Kinternally stabilizesP22}.
Under Assumption 1, it is known that the internal stability in Definition 1 and the external stability in Definition 2 are equivalent [ZDG96, Chapter 5], that is, we have
Cstab ={K|Φ∈ RH∞, withΦdefined in (3.5)}.
In fact, it is sufficient to enforce a subset of elements in Φ to be stable, as shown in [ZDG96, Lemma 5.3].
Lemma 1. UnderAssumption 1,Kinternally stabilizesP22 if and only if the closed-loop responses from (δy,δu) to (y,u) are stable, i.e.,
Φyy Φyu
Φuy Φuu
∈ RH∞.
3.2.3 The norm-minimization problem
In addition to stability, it is desirable to find a controllerK that is optimal in an appro- priate sense. A classical choice is to minimize a suitable norm of the closed-loop map from w to z, e.g., its H2 or H∞ norm. In the rest of Part I and Part II of this thesis, we will focus on theH2 norm for simplicity, as all the results related to casting a convex program hold for any system norm. By simple manipulation of (3.3) and (3.4), we derive that the problem amounts to solving the following program [ZDG96]:
minimize
K kf(K)kH2
subject to K∈ Cstab,
(3.6) wheref(K) = P11+P12K(I−P22K)−1P21. It is known that the setCstab is non-convex.
One can construct explicit examples where K1,K2 ∈ Cstab but 12(K1 +K2) ∈ C/ stab. Furthermore, f(K) is in general a non-convex function of K. Therefore, problem (3.6) is non-convex in the current form. Finally, since the order of the optimal controller Kis not known a-priori, the problem is infinite-dimensional.
3.2.4 The LQG problem as a special case and its analytical solution
The classical linear quadratic Gaussian (LQG) control problem in infinite-horizon con- siders an LTI
xk+1 =Axk+Buk+wk, (3.7)
zk=h
Q12xTk R12uTk iT
, yk =Cxk+vk,
where wk ∼ N(0, W) and vk ∼ N(0, V) for every k ∈ N, with W, V 0, Q 0 and R 0. The goal is to minimize the cost
JLQG= lim
T→∞Ew,v
"
1 T
XT k=0
xTkQxk+uTkRuk
#
= lim
T→∞Ew,v
"
1 T
XT k=0
zTkzk
# .