Systemtheorie und Regelungstechnik I - WS08/09
Formelsammlung zum Skriptum
Kapitel 2
Satz 2.3 (Lokale Existenz und Eindeutigkeit) Es sei f(x, t) st¨uckweise stetig in t und gen¨uge der Absch¨atzung (Lipschitz-Bedingung)
kf(x, t)−f(y, t)k ≤Lkx−yk, 0< L <∞
f¨ur alle x, y∈ B ={z∈ Rn | kz−x0k ≤r} und alle t ∈[t0, t0+τ]. Dann existiert ein δ >0 so, dass
˙
x=f(x, t) mit x(t0) =x0
genau eine L¨osung f¨ur t ∈ [t0, t0+δ] besitzt. Dabei wird L auch als Lipschitz-Konstante be- zeichnet.
Kapitel 3
Berechnung der Transitionsmatrix f¨ur lineare zeitkontinuierliche zeitinvariante Systeme
(a) Die Dynamikmatrix A besitzt Eigenwerte λj mit j = 1, . . . , n, f¨ur die gilt, dass die geometrische Vielfachheit gj und die algebraische Vielfachheit nj gleich sind.
Jordansche Normalform:
A˜ =
λ1 0 · · · 0 0 λ2 · · · 0 ... ... . .. ...
0 0 · · · λn
Transitionsmatrix des transformierten Systems:
Φ˜(t) =
exp (λ1t) 0 · · · 0
0 exp (λ2t) · · · 0
... ... . .. ...
0 0 · · · exp (λnt)
(b) Die DynamikmatrixAbesitzt genau einen Eigenwertλ, f¨ur den gilt, dass die geometrische Vielfachheit g echt kleiner als die algebraische Vielfachheit n ist.
Jordansche Normalform:
A˜ =
λ 1 · · · 0 0 0 λ · · · 0 0 ... ... . .. ... ...
0 0 · · · λ 1 0 0 · · · 0 λ
Transitionsmatrix des transformierten Systems:
Φ˜(t) = exp (λt)
1 t t2
2! · · · tn−1 (n−1)!
0 1 t · · · tn−2 (n−2)!
... ... ... . .. ...
0 0 · · · t
0 0 · · · 1
(c) Die Dynamikmatrix A besitzt die konjugiert komplexen Eigenwertpaare λj = αj +Iβj, λ∗j =αj−Iβj mit j = 1, . . . , r, f¨ur die gilt, dass die geometrische Vielfachheit gj und die algebraische Vielfachheit nj gleich sind.
Reelle Jordansche Normalform:
A˜ =
α1 β1 · · · 0 0
−β1 α1 · · · 0 0 ... ... . .. ... ...
0 0 · · · αr βr
0 0 · · · −βr αr
Transitionsmatrix des transformierten Systems:
Φ˜ (t) =
eα1tcos (β1t) eα1tsin (β1t) · · · 0 0
−eα1tsin (β1t) eα1tcos (β1t) · · · 0 0
... ... . .. ... ...
0 0 · · · eαrtcos (βrt) eαrtsin (βrt)
0 0 · · · −eαrtsin (βrt) eαrtcos (βrt)
Satz 3.5 (Kanonische Jordan-Form) Es sei die reellwertige (n×n)-Matrix A die Dyna- mikmatrix eines linearen, zeitinvarianten Systems. Angenommen, A habe k reelle Eigenwerte λj, j = 1, . . . , k und (n−k)/2konjugiert komplexe Eigenwerte λj =αj+Iβj (λ∗j =αj−Iβj), j = k+ 1, . . . , r mit r = (n+k)/2. Dann existiert eine regul¨are Zustandstransformation der Form
V = [v1, . . . ,vk,vk+1,Re,vk+1,Im, . . . ,vr,Re,vr,Im] (3.1) bestehend aus den Haupt- und Nebeneigenvektorenvj, j = 1, . . . , r,vi,Re =Re(vi) undvi,Im= Im(vi), i = k + 1, . . . , r so, dass die Dynamikmatrix des transformierten Systems folgende Form
A˜ =V−1AV =
U1 0 · · · 0 0 U2 · · · 0 ... ... ... ...
0 0 · · · Ul
(3.2)
mit den so genannten Jordanbl¨ocken
U=
λ 1 · · · 0 0 0 λ · · · 0 0 ... ... ... ... ...
0 0 · · · λ 1 0 0 · · · 0 λ
(3.3)
f¨ur die reellen Eigenwerte λ bzw.
U=
W E2 · · · 0 0 0 W · · · 0 0 ... ... . .. ... ...
0 0 · · · W E2 0 0 · · · 0 W
(3.4)
mit
W=
α β
−β α
und E2 = 1 0
0 1
(3.5) f¨ur konjugiert komplexe Eigenwerte α±Iβ besitzt.
Kapitel 4
Realisierungsproblem Ubertragungsfunktion¨
G(s) = yˆ(s) ˆ
u(s) = b0+b1s+· · ·+bn−1sn−1+bnsn a0+a1s+· · ·+an−1sn−1+sn (a) Realisierung als 1-te Standardform oder Steuerbarkeitsnormalform
d dt
x1
x2 ... xn−1
xn
| {z }
x
=
0 1 0 . . . 0
0 0 1 . . . 0
... ... . .. ... ...
0 0 . . . 0 1
−a0 −a1 . . . −an−2 −an−1
| {z }
A
x1
x2 ... xn−1
xn
| {z }
x
+
0 0... 0 1
| {z }
b
u
y = ˜b0 ˜b1 . . .˜bn−2 ˜bn−1
| {z }
cT
x1
x2
... xn−1
xn
| {z }
x
+ bn
|{z}
d
u
mit ˜bi =bi−aibn, i= 0,1, . . . , n−1
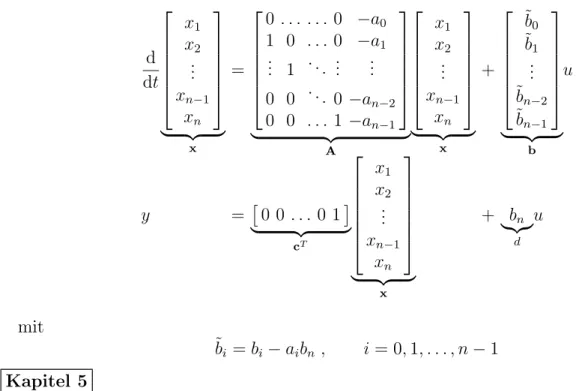
(b) Realisierung als 2-te Standardform oder Beobachtbarkeitsnormalform
d dt
x1
x2
...
xn−1
xn
| {z }
x
=
0 . . . 0 −a0
1 0 . . . 0 −a1
... 1 . .. ... ... 0 0 . .. 0 −an−2
0 0 . . . 1 −an−1
| {z }
A
x1
x2
...
xn−1
xn
| {z }
x
+
˜b0
˜b1
...
˜bn−2
˜bn−1
| {z }
b
u
y =
0 0 . . . 0 1
| {z }
cT
x1
x2
... xn−1
xn
| {z }
x
+ bn
|{z}
d
u
mit ˜bi =bi−aibn, i= 0,1, . . . , n−1
Kapitel 5
Schaltungstechnische Realisierung einiger ¨Ubertragungsfunktionen
In Abbildung 3.1 ist eine Operationsverst¨arkerschaltung in Vierpoldarstellung gezeigt.
N e t z w e r k
u = u a ,1
i= 0
a
N e t z w e r k
b
u = 0 -+
ia ,1 u a ,2ia ,2 ib ,1u b ,1 u b ,2ib ,2 y
i d e a l
Abbildung 3.1: Operationsverst¨arkerschaltung in Vierpoldarstellung.
Die ¨Ubertragungsfunktion vom Eingang uzum Ausgang y lautet G(s) = yˆ(s)
ˆ
u(s) = uˆb,2 ˆ ua,1
= ˆıb,1 Yb,12(s)
Ya,21(s) ˆıa,2
=−Ya,21(s) Yb,12(s) .
Da passiveRLC-Netzwerke reziprok sind, gilt allgemein, dass die Admittanzmatrix symme- trisch ist, d.h.Y12(s) =Y21(s). Der nachfolgenden Tabelle sind die Leitwerte einiger Netzwerke zu entnehmen, womit sich verschiedene ¨Ubertragungsfunktionen als Operationsverst¨arkerschaltung realisieren lassen.
Schaltung Y12 Koeffizienten
R −1
R
C
−sC
CR
−V (1 +sT)
V = 1 R T =RC
CR R
3
− V
(1 +sT)
V = 1 2R T = RC
2
C
R 1
R 2
−V 1 +sT 1 +sηT η <1
V = 1 R1
T = (R1+R2)C η = R2
R1+R2
CR 2
R 1 R 1
−V 1 +sηT 1 +sT η <1
V = 2R1 +R2
2R1R2
T = R1C 2 η= 2R1
2R1+R2
Kapitel 6
Satz 6.3 (Routh-Hurwitz Verfahren) Ein Polynom n(s) der Form n(s) =
Xn j=0
ajsj
mit den reellen Koeffizienten aj, j = 1, . . . , n, ist genau dann ein Hurwitzpolynom, wenn alle Elemente der Pivotspalte des nachfolgenden Routh-Schemas
sn a01=an a02 =an−2 a03 =an−4 . . . sn−1 a11=an−1 a12 =an−3 a13 =an−5 . . .
sn−2 a21 a22 a23 . . .
sn−3 a31 a32 a33 . . .
... ... ... ... . ..
s1 an−1,1 0 0 . . .
s0 an,1
Pivotspalte mit
aij = ai−1,1ai−2,j+1−ai−2,1ai−1,j+1
ai−1,1
f¨ur i= 2,3, . . . , n und j = 1,2, . . . von Null verschieden sind und gleiches Vorzeichen besitzen.
Satz 6.4 (Kriterium von Michailov) Ein Polynom n(s) vom Grad n ist genau dann ein Hurwitzpolynom, wenn
∆ arg (n(Iω)) =nπ gilt.
r L ( s ) y
Abbildung 6.2: Geschlossener Regelkreis
Satz 6.5 (Nyquist-Kriterium) Der geschlossene Regelkreis Tr,y(s) nach Abbildung 6.2 mit der ¨Ubertragungsfunktion des offenen KreisesL(s)ist genau dann BIBO-stabil, wenn die stetige Winkel¨anderung von 1 +L(s) folgender Bedingung
∆ arg (1 +L(Iω)) = (max (grad (zL), grad (nL))−N−(nL) +N+(nL))π gen¨ugt.
Definition 6.3 (Nyquist-Kriterium bei ¨Ubertragungsfunktionen vom einfachen Typ) Man nennt eine ¨Ubertragungsfunktion L(s) vom einfachen Typ, wenn sie sich in der Form
L(s) = V sρ
zL(s)
nL(s) , zL(0) =nL(0) = 1 (6.6) mit den teilerfremden Polynomen zL(s) und sρnL(s) darstellen l¨asst, wobei nachfolgende Be- dingungen erf¨ullt sind:
(A) Das Polynom nL(s) ist ein Hurwitzpolynom und f¨ur ρ gilt ρ∈ {0,1}, (B) grad (nL(s)) +ρ >grad (zL(s)),
(C) die Betragskennlinie von L(Iω) weist genau einen Schnittpunkt mit der0-dB-Linie (eine Durchtrittsfrequenz ωC) auf bzw. die Ortskurve von L(Iω) schneidet den Einheitskreis genau einmal und
(D) der Verst¨arkungsfaktor V ist positiv.
Unter diesen Voraussetzungen ist der Regelkreis nach Abbildung 6.2 mit der ¨Ubertragungsfunktion des offenen Kreises L(s) genau dann BIBO-stabil, wenn der Abstand der Phase an der Durch- trittsfrequenz arg (L(IωC)) zu −π, die so genannte Phasenreserve Φ,
Φ = arg (L(IωC)) +π positiv ist.
Kapitel 7
Lead-Lag-Reglerentwurf
(a) Ein Lead-Glied besitzt eine ¨Ubertragungsfunktion der Form RLead(s) = 1 +sTLead
1 +sηLeadTLead
, 0< ηLead <1 .
Will man eine maximale Phasenanhebung von ∆ϕLead an der Stelle ωC erreichen, so berechnen sich die Koeffizienten TLead und ηLead zu
ηLead = 1 + 2 tan (∆ϕLead)
tan (∆ϕLead)− q
tan (∆ϕLead)2+ 1
, TLead = 1
√ηLeadωC
.
(b) Ein Lag-Glied besitzt eine ¨Ubertragungsfunktion der Form RLag(s) = 1 +sTLag
1 +sηLagTLag
, ηLag >1 .
Will man eine Betragsabsenkung um ∆aLag und eine Phasenabsenkung um ∆ϕLag an der Stelle ωC erreichen, so berechnen sich die Koeffizienten TLag und ηLag zu
TLag = ∆aLag
q
1 + tan (∆ϕLag)2−1 ωCtan (∆ϕLag) , ηLag = ωCTLag−tan (∆ϕLag)
ωCTLag(1 +ωCTLagtan (∆ϕLag)) .
Allgemeine Formeln
Eigenschaften der Laplace-Transformation I. Linearit¨at:
Zeitbereich: c1f1(t) +c2f2(t) , c1, c2 ∈C Bildbereich: c1fˆ1(s) +c2fˆ2(s)
II. ¨Ahnlichkeitssatz:
Zeitbereich: f(at) , a >0 Bildbereich: 1
afˆs a
III. Erster Verschiebungssatz:
Zeitbereich: f(t−a)σ(t−a) , a >0 Bildbereich: e−asfˆ(s)
IV. Zweiter Verschiebungssatz:
Zeitbereich: f(t+a) , a >0 Bildbereich: eas
fˆ(s)−Ra
0 f(t)e−stdt V. D¨ampfungssatz:
Zeitbereich: e−ctf(t) , c∈C Bildbereich: fˆ(s+c)
VI. Differentiation:
Zeitbereich: d
dtf(t) = ˙f(t) Bildbereich: sfˆ(s)−f(+0) bzw.
Zeitbereich: dn
dtnf(t) =f(n)(t)
Bildbereich: snfˆ(s)−f(+0)sn−1−f(1)(+0)sn−2−. . .−f(n−1)(+0) VII. Integration:
Zeitbereich: Rt
0 f(τ) dτ Bildbereich: 1
sfˆ(s)
VIII. Umkehrung zu VI:
Zeitbereich: (−t)nf(t) Bildbereich: dn
dsnfˆ(s) IX. Umkehrung zu VII:
Zeitbereich: 1 tf(t) Bildbereich: R∞
s fˆ(σ) dσ X. Faltungssatz:
Zeitbereich: (f1∗f2) (t) =Rt
0 f1(τ)f2(t−τ) dτ =Rt
0 f1(t−τ)f2(τ) dτ Bildbereich: fˆ1(s) ˆf2(s)
XI. Periodische Funktionen:
Zeitbereich: f(t+T) =f(t) Bildbereich: 1
1−e−sT RT
0 e−stf(t) dt
XII. Grenzwerts¨atze: (nur anwendbar, wenn die Grenzwerte auch existieren) Anfangswertsatz: limt→+0f(t) = lims→∞sfˆ(s)
Endwertsatz: limt→+∞f(t) = lims→0sfˆ(s)
Korrespondenzen der Laplace-Transformation
Nummer Zeitbereich Bildbereich f(t) fˆ(s)
I. δ(t) 1
II. σ(t) 1
s
III. t 1
s2
IV. eat 1
s−a
V. tneat n!
(s−a)n+1
VI. sin (bt) b
s2+b2
VII. cos (bt) s
s2+b2 VIII. eatsin (bt) b
(s−a)2+b2 IX. eatcos (bt) s−a
(s−a)2+b2
Tabelle 8.1: Laplace-Korrespondenztabelle einiger wichtiger Funktionen.
Einige trigonometrische Beziehungen
sin(0) = 0 cos(0) = 1
sin( π 12) =
√2(√ 3−1)
4 cos( π
12) =
√2(√ 3 + 1) 4 sin(π
6) = 1
2 cos(π
6) =
√3 2 sin(π
4) =
√2
2 cos(π
4) =
√2 2 sin(π
3) =
√3
2 cos(π
3) = 1 2 sin(5π
12) =
√2(√ 3 + 1)
4 cos(5π
12) =
√2(√ 3−1) 4 sin(π
2) = 1 cos(π
2) = 0 tan(0) = 0
tan(π
12) = 2−√ 3 tan(π
6) =
√3 3 tan(π
4) = 1 tan(π
3) =√ 3 tan(5π
12) = 2 +√ 3 tan(π
2) =∞