2.3.6 Wirbel des Magnetfeldes

(1)

Uberf¨¨ uhrt man den Fluss mit dem Satz von Gauss in ein Volumenintegral, so ergibt sich die lokale Form:

Differentielle Form der ersten Maxwell-Gleichung:

divE(r, t) =kqρ(r, t) (2.49)

2.3.4 Quellen des Magnetfeldes

Die Frage ist jetzt, ob punktförmige Quellen für das MagnetfeldB existieren. Das Experiment hat bisher keine gefunden, sondern bisher nur dipolartige Felder festellen können¹⁶. Also folgt für die Quellen des Magnetfeldes:

Lokale Form der zweiten Maxwell-Gleichung:

divB(r, t) = 0 (2.50)

Integralform der zweiten Maxwell-Gleichung:

I

F

B df= 0 (2.51)

2.3.5 Wirbel des elektrischen Feldes

Versuche der Form, dass man einen Stabmagnet durch eine LeiterschleifeLbewegt und einen Stromfluss misst, f¨uhrten zur Entdeckung des Induktionsgesetzes durch Faraday. Dabei entsteht ein Stromfluss in vielen unter- schiedlichen Situationen, z.B. bei

• einer zeitlichen ¨Anderung des Magnetfeldes→ _dt^dB 6= 0 ,

• Bewegung der KonturL relativ zum Magnetfeld,

• Deformation der KonturL.

16Bei der Existenz magnetischer Monopole wären die Feldgleichungen vollständig symmetrisch bezüglich E und B. Entsprechende Modelle gehen auf P. Curie und P. Dirac zurück. Es existieren bestimmte Festkörpersysteme (z.B. Spineis), deren Hamiltonoperator die selbe Form, hat wie der für ein System aus Magnetischen Monopolen, s. z.B. Ref. [Bon11].

(2)

Abbildung 2.11: Versuch zum Induktionsgesetz. Ein Strom wird in einer Leiterschleife L induziert, wenn sich der Fluss des Magnetfeldes durch die vonLbegrenzte Fl¨acheAzeitlich ¨andert.

Man fasst alle diese Effekte in einer einzigen Gr¨oße zusammen: dem magnetische Fluss ΦB|A(L)des Magnetfeldes durch die vonLbegrenzte Fl¨acheA,

ΦB|A(L)= Z

A(L)

B df .

Der induzierte Strom ist also verkn¨upft mit einer zeitlichen ¨Anderung von ΦB. Andererseits ist ein Stromfluss I die Reaktion auf eine induzierte Spannung, die wir, wegen der Geometrie, alsRingspannung UR bezeichnen.

Der Zusammenhang zwischen elektrischem Feld und Spannung ist hier als Verallgemeinerung des Falls eines homogenen elektrischen Feldes zwischen zwei parallelen Elektroden, U =E·d, wobei dder Abstand ist, aus Abbildung 2.12 zu erkennen:

Abbildung 2.12: Elektrisches Feld zwischen zwei Kondensator-Platten im Abstandd. Das Feld ist parallel zum Verbindungsvektord.

die Spannung, die in einem kleinen Kontur-Element erzeugt wird, ist dUR=X

i

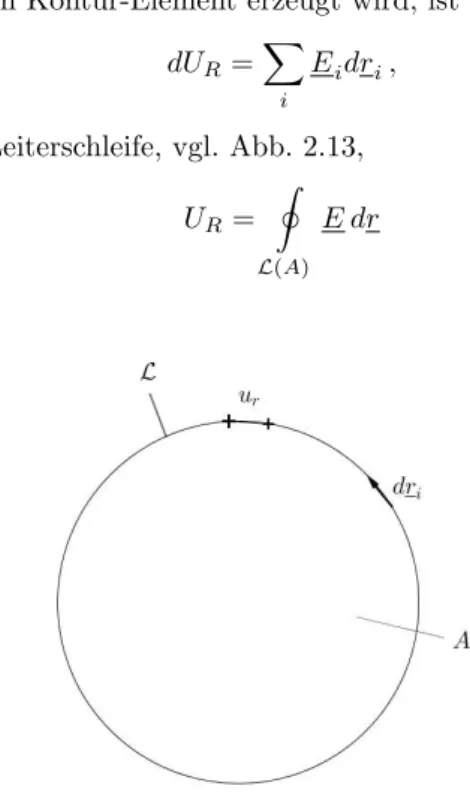
E_idr_i, und damit folgt f¨ur die gesamte Leiterschleife, vgl. Abb. 2.13,

UR= I

L(A)

E dr

Abbildung 2.13: Berechnung der induzierten Ringspannung in einem geschlossenen LeiterL.

(3)

A

rotE+kB

dtB df = 0 (2.54)

Letzteres gilt für eine beliebige Fläche. Damit müssen die Integranden gleich sein, und es folgt das Resultat für die Wirbel des elektrischen Feldes, und damit die

Lokale Form der dritten Maxwell-Gleichung:

rotE(r, t) =−kB

d

dtB(r, t) (2.55)

Integralform der dritten Maxwell-Gleichung:

I

L(A)

E(r, t)dr=−kB

d dt

Z

A

B(r, t)df (2.56)

2.3.6 Wirbel des Magnetfeldes

Wir fragen uns jetzt, was die Ursachen für ein magnetisches Wirbelfeld sind. Das Experiment zeigt, dass ein StromIein Magnetfeld erzeugt (Ampere-Gesetz). Dieses Magnetfeld ist ein Wirbelfeld (geschlossene Feldlinien), und der Betrag der Feldstärke folgt folgender Proportionalität:

B∝ I r

Die Orientierung dieses Magnetfeldes ergibt sich aus dem Experiment parallel zum Vektor ˆeϕ in Zylinderkoor- dinaten, s. Abb. 2.14 und folgt aus der Symmetrie des Problems.

I ˆ eϕ

B

L

Abbildung 2.14: Ringf¨ormiges Magnetfeld in Folge eines Stroms (d¨unner unendlich langer Leiter), senkrecht zur Blattebene (aus der Ebene heraus)

Durch Einf¨uhrung der experimentell beobachteten Konstanten, vgl. Tab. 2.2, ergibt sich die Gleichung¹⁷ B(r) = kI

2π I r, mit: kI =

(4π

c , CGS µ0, SI

17Details werden wir im Kapitel Magnetostatik best¨atigen und verallgemeinern.

(4)

Analog zum Vorgehen des vorigen Abschnitts finden wir die “magnetische Ringspannung” (oder Zirkulation des B-Feldes):

I

L

B(r)dr=B(r)2πr= kI

2π I

r2πr=kI ·I,

die durch den StromIhervorgerufen wird. Die Auswertung des Linienintegrals im ersten Schritt ist in Ordnung, daLeinen Kreis mit Radiusrparametrisiert und aus dem Experiment folgte, dassB(r) auf einem solchen Kreis konstant ist.

Damit haben wir das Resultat f¨ur das elementare Beispiel eines einzelnen d¨unnen, geraden, unendlich langen Leiters gefunden. Dieses Ergebnis wird wieder schrittweise verallgemeinert:

1. Es liegen nunN Str¨ome vor, die parallel zu einander seien. Dann gilt I^Ges=

XN

i=1

Ii,

und das Magnetfeld wird durch I^Ges erzeugt. Dies gilt natürlich wieder nur unter der Annahme von Additivität und der Unabhängigkeit der Einzelströme (Superpositionsprinzip).

2. Analog zum Vorgehen bei der Ladungsdichte, möchten wir jetzt auch Ströme mit endlicher Ausdehnung betrachten. Zusätzlich sollen die Einzelströme beliebige Orientierung besitzen dürfen. Wir führen daher folgende Ersetzung durch:

I^Ges:X

i

Ii→ Z

F(L)

jdf

Es folgt die vorl¨aufige Form der vierten Maxwell-Gleichung (Integralform):

I

L

B dr=kII^Ges|_F(L) (2.57)

Der Übergang zur lokalen Form geschieht mit dem Satz von Stokes und dem Argument, dass die Inte- granden übereinstimmen müssen (beliebige KonturL)

Z

F(L)

rotB df =kI

Z

F(L)

j df

⇒rotB(r, t) =kIj(r, t). (2.58)

Dies ist die vorl¨aufige lokale Form der 4. Maxwell-Gleichung. Diese Maxwell-Gleichung wollen wir noch te- sten, indem wir die Divergenz dieser Gleichung bilden. Nach dem Fundamentalsatz m¨usste die Divergenz der Wirbeldichte des magnetischen Feldes, rotB, immer gleich Null sein. Hieraus folgt dann aber auch zwingend:

divj(r, t) = 0

Dies ist ein Ergebnis, das fragw¨urdig erscheint. Wir zeigen mit Hilfe der Kontinuit¨atsgleichung den auftretenden Widerspruch. Nach dieser gilt:

∂ρ

∂t + divj= 0, so dass obiges Ergebnis f¨ur die Stromdichte die Konsequenz h¨atte

˙

ρ(r, t) = 0.

Das heißt, es dürfte keine zeitlich veränderliche Ladungsdichte geben. Das kann nicht allgemeingültig sein, und damit kann die obige Form der 4. Maxwell-Gleichung nicht korekt sein.

Ein weiterer Widerspruch wird evident, wenn man man die Zeitableitung der ersten Maxwell-Gleichung bildet:

div ˙E(r, t) =kqρ(r, t) = 0˙ .

(5)

Kombination von Kontinuit¨atsgleichung und erster Maxwell-Gleichung folgt nun, ¨ahnlich wie oben:

˙ ρ= 1

kq

div ˙E=−divj^s

⇒div

j^s+ ˙E 1 kq

= 0

⇒j^s=−1 kq

E .˙

Dies ist ein bemerkenswertes Ergebnis: die zeitliche ¨Anderung des elektrischen Feldes hat die selbe Wirkung wie eine Ladung: sie bewirkt einen Strom. Hiermit folgt die korrekte differentielle Form der vierten Maxwell- Gleichung zu:

Lokale Form der vierten Maxwell-Gleichung:

rotB=kI

j+ 1

kq

E˙

(2.60)

Die integrale Form dieser vierten Maxwell-Gleichung erhält man durch Integration über die Fläche und an- schließende Anwendung des Satzes von Stokes auf die linke Seite:

Integrale Form der vierten Maxwell-Gleichung:

I

L(F)

Bdr=kI

Z

F(L)

j+ 1

kq

E˙

df (2.61)

Wir besprechen nun ein Beispiel f¨ur einen Verschiebungsstromj^sohne Existenz bewegter Ladungen. Betrachte folgende Skizze eines kurzschließbaren Kondensators, Abb. 2.15:

Abbildung 2.15: Beim Kurzschließen des Kondensators bricht das Feld zusammen. Die zeitliche ¨Anderung von E hat die gleiche Wirkung wie ein Stromfluss (“Verschiebungsstrom”) und f¨uhrt ebenfalls zur Erzeugung eines Magnetfelds.

Ein Schließen dieses Schalters bewirkt nach endlicher Zeit E = 0. Zuvor ist jedoch ^∂E_∂t 6= 0, daher ist die Verschiebungsstromdichte js6= 0 und bewirkt, nach der vierten Maxwell-Gleichung, ein magnetisches Wirbel- feld. Da nun eine ¨Anderung eines magnetischen Feldes stattgefunden hat, entsteht wiederum nach der dritten

(6)

Maxwell-Gleichung ein elektrisches Feld. Dieser Prozess kann sich mit der Zeit und im Raum immer weiter fortsetzen. Das Experiment best¨atigt vielfach diese wechselseitige Kopplung. Das bekannteste Beispiel sind die hierbei entstehenden elektromagnetischen Wellen, die Maxwell auf Grundlage dieser Gleichungen vorhergesagt hatte.

Damit ist der Widerspruch in der vorläufigen Formulierung der vierten Maxwell-Gleichung aufgelöst, und wir können die Gleichung korrigieren. In folgender Tabelle fassen wir noch einmal die Ergebnisse dieses Abschnitts zusammen:

Maxwell-Gleichung Differentielle Form Integralform Experimente

1 divE=kqρ H

F

Edf=kq R

V(F)

ρdV =kqQ^Ges_V Coulombgesetz

2 divB= 0 R

F

Bdf = 0 ∄magn. Monopole

3 rotE=−kBB˙ H

L

Edr=−kB d dt

R

F(L)

Bdf Induktionsgesetz

4 rotB=kI

j+ ^E^˙

kq

H

L

Bdr=kI R

F(L)

j+ ^E^˙

kq

df Ampère Gesetz, Verschiebungsstrom Tabelle 2.3: Maxwell-Gleichungen in differentieller und integraler Form. In der lokalen Form hängen beide Seiten der Gleichung vonrundtab. Die angegebenen Experimente stellen nur Beispile dar. Die angegebene Form ist unabhängig vom Einheitensystem, die SI- und CGS-Versionen folgen aus Tabelle 2.2.

Durch Verwendung der Konstanten ist diese Schreibweise unabh¨angig vom Einheitensystem.

2.3.6.1 Diskussion der L¨osung

• Die Maxwell-Gleichungen sind die Bewegungsgleichungen f¨ur die FelderE undB. Die Struktur der Glei- chung ergibt, dass beide Felder gekoppelt sind.

• Es gibt jeweils zwei Gleichungen f¨urE undB, als Konsequenz des Fundamentalsatzes.

• Das Gesamtfeld besteht aus der Summe von wirbelfreien und quellenfreien Anteilen.

• Insgesamt zählt man 8 skalare Gleichungen für 6 Unbekannte Größen (Ex, ..., Bz). Es stellt sich also die Frage, ob das Problem überbestimmt ist. Diese Frage wird im Abschnitt 2.5, im Zusammenhang mit der Eichung geklärt.

2.3.6.2 Maxwell-Gleichungen im CGS-System

Im CGS-System notieren wir die Gleichungen unter Verwendung von Tabelle 2.2 folgendermaßen:

divE(r, t) = 4πρ(r, t), divB(r, t) = 0

rotE(r, t) =−1 c

∂

∂tB(r, t), rotB(r, t) =4π

c j(r, t) +1 c

∂

∂tE(r, t) Zus¨atzlich ben¨otigen wir physikalische Randbedingungen. Insbesondere ist zu fordern:

|r|→∞lim









 E B

∂

∂tE

∂

∂tB

∂

∂rE

∂

∂rB

= 0

Das ergibt sich aus der Endlichkeit von Energie und Impuls des elektromagnetischen Feldes, die wir im Ab- schnitt 2.4 kennenlernen werden.

(7)

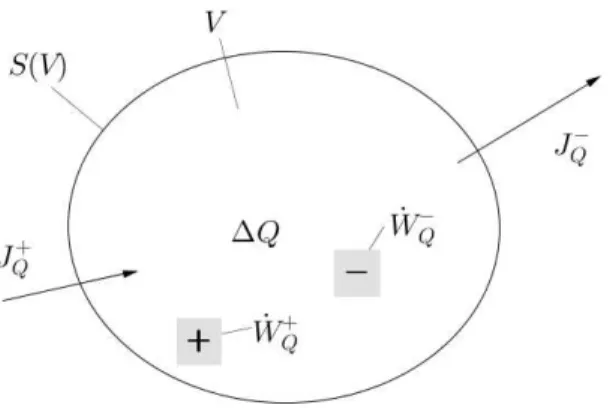
Abbildung 2.16: Gesamtbilanz der GrößeQim VolumenV. ∆Qändert sich durch Zu- und AbflussbeiträgeJ_Q^± durch die OberflächeS sowie durch Erzeugungs- und Vernichtungsbeiträge ˙W_Q^± im Volumen.

Es gilt also ganz allgemein folgende Bilanz-Gleichung (ein globaler Erhaltungssatz):

∂

∂t∆Q

V

=J_Q⁺−J_Q⁻+ ˙W_Q⁺−W˙_Q⁻ (2.62) Ein Beispiel, das wir schon kennen, ist die Erhaltung der Ladung. Wir werden im Folgenden sehen, dass ähnliche Bilanzgleichungen auch für die Energie und den Impuls des elektromagnetischen Feldes gelten. Dafür müssen wir die entsprechenden Beiträge in Gleichung (2.62) identifizieren. Wir kennen zwar bereits die Bewegungs- gleichung der Felder, wissen aber noch nichts darüber, welche Größen die Energie und den Impuls des Feldes charakterisieren. Zu diesem Zweck beginnen wir die Betrachtung mit der Energie und dem Impuls geladener Teilchen, die mit dem Feld wechselwirken.

2.4.2 Mechanische Energie-/Impulsbilanz von Ladungen

BetrachteN Punktteilchen mit den Massenmi. F¨ur die gesamte kinetische Energie T und den Gesamtimpuls P ergibt sich:

T = XN

i=1

mi

2 r˙²_i P=

XN

i=1

mir˙_i

Jetzt betrachten wir die zeitliche ¨Anderung dieser beiden Gr¨oßen, was der Leistungsformulierung des Energie- satzes und dem Impulssatz entspricht:

Energiesatz: T˙ =

XN

i=1

mir˙_i¨r_i= XN

i=1

F_ir˙_i

Impulssatz: P˙ =

XN

i=1

mi¨r_i= XN

i=1

F_i

(8)

Jetzt nehmen wir dieses allgemeine mechanische Resultat und wenden es auf den Fall geladener Teilchen an, die sich in einem elektromagnetischen Feld befinden. Dazu ersetzen wir die KraftFidurch die kombinierte Lorentz- und Coulombkraft von Teilchen der Ladungqi:

F_i=qi

h

E(r_i, t) +kBr˙_i×B(r_i, t)i

. (2.63)

Setzt man dies in obige Gleichungen ein, so ergeben sich:

P˙ = XN

i=1

qi

h

E(r_i) +kBr˙_i×B(r_i)i

, (2.64)

T˙ = XN

i=1

qi

E(r_i) ˙r_i+kBr˙_i×B(r_i)

| {z }

⊥˙r_i

◦r˙_i

| {z }

=0

= XN

i=1

qiE(r_i) ˙r_i. (2.65)

Das heißt, das Magnetfeld verrichtet keine Arbeit an einer Punktladung. Jetzt führen wir wieder die Verallge- meinerung von Punktladungen und Strömen auf allgemeine Verteilungen durch und führen dazu zunächst die Ladungs- und Stromdichte für ein System von Punktladungen ein:

Ladungsdichte: ρP L(r, t) =

XN

i=1

qiδ[r−r_i(t)]

Stromdichte: j_{P L}(r, t) =

XN

i=1

qir˙_i(t)δ[r−r_i(t)]

Im Weiteren wenden wir folgende Verallgemeinerung an:

X

i

qi→ Z

V

ρ(r)dV und nutzen dabei folgende Eigenschaft der Delta-Funktion:

Z

f(r)δ[r−r_i]dV =f(r_i)

Mit Hilfe dieser Ersetzungen kann man Gleichung (2.65) wie folgt schreiben ( Überprüfung durch Rückeinsetzen):

T˙(t) = Z

j(r, t)◦E(r, t)dV (2.66)

Weiter definiere:

T˙(t) = Z

t(r, t)dV,˙ mit

t(r, t) =˙ j(r, t)◦E(r, t) = Energiedichte

Zeit = Leistungsdichte (2.67)

Analog kann man Gleichung (2.64) wie folgt formulieren:

P˙(t) = Z

ρ(r, t)E(r, t) +kBj(r, t)×B(r, t)

dV , (2.68)

und wir definieren wieder:

P(t) =˙ Z

˙

p(r, t) d³r, (2.69)

mit

˙

p(rt) =ρ(r, t)E(r, t) +kBj(r, t)×B(r, t) = Impulsdichte

Zeit = Kraftflussdichte. (2.70) Aus diesen Formeln und den Maxwell-Gleichungen leiten wir jetzt die Energie- und Impulsbilanz des elektromagnetischen Feldes her.

(9)

c c

Nun nehmen wir die die dritte Maxwell-Gleichung und multiplizieren diese mitB:

rotE=−1 cB˙ B·rotE=−1

cB·B˙ (2.72)

Nun berechnen wir die Differenz der Gleichungen (2.71) und (2.72):

E·rotB−B·rotE=4π

c j·E+1

cE·E˙ +1 cB·B˙ E·rotB−B·rotE=4π

c j·E+ 1 2c

∂

∂t(E²+B²) (E·rotB−B·rotE)

| {z }

div(B×E)

c

4π =j·E+ ∂

∂t

E²+B² 8π

−div(E×B) =j·E+ ∂

∂t

(E²+B²) 8π

−j·E= ∂

∂t

(E²+B²)

8π + div(E×B)

Diese Gleichung hat bereits die Form eines lokalen Erhaltungssatzes f¨ur die Energie pro Volumen. Wir identifizieren darin dieEnergiedichtedes elektromagnetischen Feldes:

u(r, t) := E²(r, t) +B²(r, t)

8π (2.73)

und außerdem den Vektor derEnergiestromdichte (auchPoynting-Vektorgenannt):

S(r, t) = c

4πE(r, t)×B(r, t) (2.74)

Schließlich interpretieren wir den Term−j·Eals zeitliche ¨Anderung der Feldenergiedichte durch Wechselwirkung mit Materie (mit Ladungen). Er beschreibt also den Energieaustausch zwischen Feld und Ladung. Wir verwenden daf¨ur die Notation ˙w^←−−_{F M}. Es gilt:

˙ w^←−−_{F M}







0, Feldenergie bleibt erhalten

>0, Feld gewinnt Energie

<0, Feld verliert Energie

Mit diesen Gr¨oßen wird die Energiebilanz f¨ur das elektromagnetische Feld zu:

(10)

∂

∂tu(r, t) + divS(r, t) = ˙w^←−−_{F M}(r, t) (2.75)

Die Energieerhaltung gilt also nicht für das Feld allein. Betrachtet man die Energiebilanz aus der Sicht der Teilchen, so gilt für die Leistungsdichte der Materie (d.h. der Ladungen, zur Verdeutlichung fügen wir dem Subskript “M” an):

t˙M = ˙w^←−−_{F M}=−w˙^−−→_{F M} Die Energiebilanz des gesamten Systems hat also folgende Form:

∂

∂t

u(r, t) +tM(r, t)

+ divS(r, t) = 0 (2.76)

Lokale Form der Energiebilanz f¨ur Feld plus Teilchen

Das System ist abgeschlossen, wenn keine anderen Kräfte als die Lorentzkraft (z.B. Reibungskräfte oder Gravi- tationskraft) relevant sind. Die globale Form der Energiebilanz folgt aus der lokalen Form wieder, indem man obige Gleichung über das VolumenV integriert:

Z

V

∂

∂t(u+tM) + divS

dV = ∂

∂t Z

V

(u(r, t) +tM(r, t))dV + I

F(V)

S(r, t)df= 0,

wobei wir beim Integral über den Poynting-Vektor den Satz von Gauss angewendet haben und F(V) die das VolumenV einschließende Oberfläche ist. Die Größe H

F(V)

Sdf:= ΦS ist der Fluss der Energiestromdichte (des Poynting-Vektors) durch die OberflächeF. Da das Integral über die Leistungsdichte der Materie die kinetische EnergieT ist, können wir die globale Energiebilanz auch in folgender Form schreiben:

∂

∂t[WEM+T] + I

F(V)

Sdf = 0 (2.77)

Globale Form der Energiebilanz f¨ur Feld plus Teilchen Hierbei k¨onnen wir ablesen:

WEM = Z

V

E²(r, t) +B²(r, t)

8π d³r (2.78)

Gesamtenergie des elektromagnetische Feldes.

Betrachte den Spezialfall, dassV =R³ist. Dann wird der Fluss durch die Oberfl¨acheF gleich Null, da das Feld im Unendlichen verschwindet, und es gilt:

∂

∂t[WEM+T] = 0, (2.79)

das heißt, die Summe aus Teilchen- und Feldenergie im gesamten Raum bleibt erhalten.

2.4.4 Impulsbilanz

Wir starten nun bei Gleichung (2.70), die wir im CGS-System aufschreiben (kB = 1/c),

˙

p=ρ(r, t)E(r, t) +1

cj(r, t)×B(r, t),