HochschuleRheinMain Kryptologie

(1)

Skript zur Vorlesung

Kryptologie

Wintersemester 2013/2014

Prof. Dr. Steffen Reith Steffen.Reith@hs-rm.de

Hochschule RheinMain

Fachbereich Design Informatik Medien

Erstellt von: Eugen Wittmann Zuletzt überarbeitet von: Steffen Reith

Email: Steffen.Reith@hs-rm.de Erste Version: August 2006

Version: 1371 Date: 2015-06-16

(2)

(3)

Nichts ist getan, wenn noch etwas zu tun übrig ist.

Carl Friedrich Gauß

je n’ai pas le temps Évariste Galois

Dieses Skript ist aus der Vorlesung „Kryptographische Algorithmen“ des Diplom-Studiengangs Informatik und der Vorlesung „Kryptologie“ des Masterstudiengangs Informatik an der Hoch- schule RheinMain (früher Fachhochschule Wiesbaden) hervorgegangen. Ich danke allen Höreren dieser Vorlesungen für konstruktive Anmerkungen und Verbesserungen. Insbesondere möchte ich Herrn Mykhailo Moldavskyy und besonders Herrn Patrick Vogt für ihre Verbesserungsvor- schläge danken. Naturgemäß ist ein Skript nie fehlerfrei (ganz im Gegenteil!) und es ändert (mit Sicherheit!) sich im Laufe der Zeit. Deshalb bin ich auf weitere Verbesserungvorschläge

angewiesen.

(4)

(5)

Inhaltsverzeichnis

1. Klassische Public-Key Kryptographie 1

1.1. Einige Grundlagen der Rechnerarithmetik . . . 1

1.1.1. Stellenwertsysteme . . . 1

1.1.2. Die klassischen Algorithmen . . . 1

1.1.2.1. Die Addition und Subtraktion . . . 1

1.1.2.2. Die Multiplikation . . . 3

1.1.2.3. Die Division . . . 5

1.1.2.4. Die Exponentiation . . . 8

1.2. Einige Grundlagen aus der elementaren Zahlentheorie . . . 8

1.2.1. Der größte gemeinsame Teiler . . . 9

1.2.2. Restklassenringe . . . 11

1.3. Das RSA Public-Key Kryptosystem . . . 12

1.3.1. RSA – Schlüsselerzeugung . . . 12

1.3.2. RSA – Ver- und Entschlüsselung . . . 14

1.4. Digitale Signaturen . . . 14

1.5. Angriffe auf RSA . . . 15

1.6. Primzahlerzeugung . . . 16

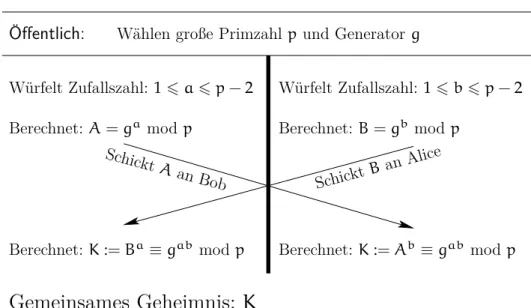
2. ECC – Elliptic Curve Cryptography 18 2.1. Der klassische Diffie-Hellman Schlüsselaustausch & Diskrete Logarithmen . . . . 18

2.2. Einige Grundlagen . . . 20

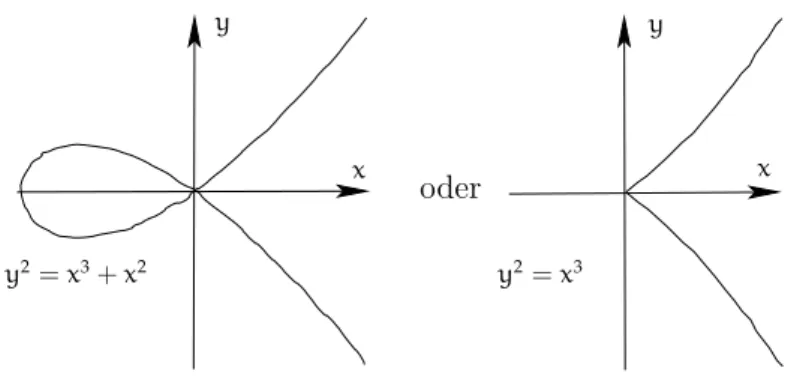
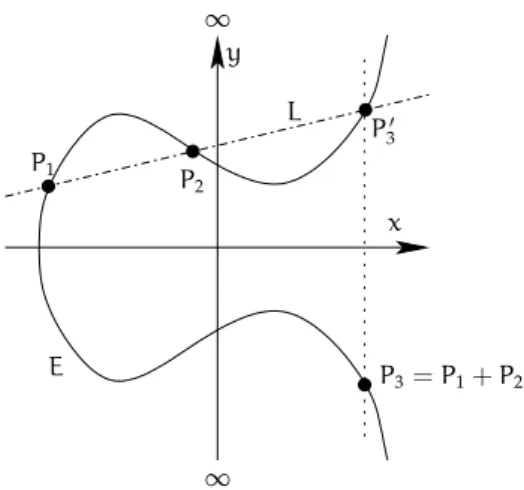
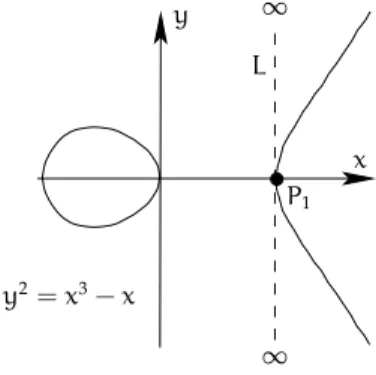
2.3. Das Gruppengesetz . . . 23

2.4. Der Diffie-Hellman Key-Exchange mit Elliptischen Kurven . . . 26

3. Symmetrische Kryptosysteme 27 3.1. Blockchiffren . . . 28

3.2. Stream Ciphers . . . 28

3.3. Einige Grundlagen über endliche Körper . . . 29

3.4. AES – Advanced Encryption Standard . . . 31

3.5. Modes of Operation . . . 34

4. Hashfunktionen und Anwendungen 36 4.1. Die Merkle-Damgård Konstruktion (Merkle’s meta method) . . . 37

4.2. Challenge-Response Verfahren. . . 39

5. Zero-Knowledge Protokolle 39 5.1. Das Fiat-Shamir Protokoll . . . 41

A. Grundlagen und Schreibweisen 43 A.1. Mengen . . . 43

A.1.1. Die Elementbeziehung und die Enthaltenseinsrelation . . . 43

A.1.2. Definition spezieller Mengen . . . 43

A.1.3. Operationen auf Mengen. . . 44

A.1.4. Gesetze für Mengenoperationen . . . 44

A.1.5. Tupel (Vektoren) und das Kreuzprodukt . . . 45

A.1.6. Die Anzahl von Elementen in Mengen . . . 45

A.2. Relationen und Funktionen . . . 46

A.2.1. Eigenschaften von Relationen . . . 46

A.2.2. Eigenschaften von Funktionen. . . 46

A.2.3. Permutationen . . . 47

(6)

Inhaltsverzeichnis

A.3. Summen und Produkte. . . 48

A.3.1. Summen . . . 48

A.3.2. Produkte . . . 49

A.4. Gebräuchliche griechische Buchstaben . . . 50

B. Einige formale Grundlagen von Beweistechniken 50 B.1. Direkte Beweise . . . 51

B.1.1. Die Kontraposition . . . 52

B.2. Der Ringschluss . . . 52

B.3. Widerspruchsbeweise . . . 53

B.4. Der Schubfachschluss . . . 53

B.5. Gegenbeispiele . . . 54

B.6. Induktionsbeweise und das Induktionsprinzip . . . 54

B.6.1. Die vollständige Induktion . . . 54

B.6.2. Induktive Definitionen . . . 56

B.6.3. Die strukturelle Induktion . . . 56

C. Komplexität 59 C.1. Effizient lösbare Probleme: die KlasseP . . . 59

C.1.1. Das Problem der 2-Färbbarkeit . . . 61

C.2. Effizient überprüfbare Probleme: die KlasseNP . . . 64

C.3. Schwierigste Probleme inNP: der Begriff derNP-Vollständigkeit . . . 67

C.3.1. Traveling Salesperson istNP-vollständig . . . 69

C.4. Die Auswirkungen derNP-Vollständigkeit . . . 70

C.5. Der Umgang mitNP-vollständigen Problemen in der Praxis . . . 72

Stichwortverzeichnis 77

Literatur 81

(7)

1. Klassische Public-Key Kryptographie

Die Grundlage der Public-Key Kryptographie ist die Idee, einen öffentlichen Verschlüsselungs- schlüssel (im „Telefonbuch“) und einen geheimen Entschlüsselungsschlüssel zu verwenden. Dabei soll es unmöglich sein, aus dem öffentlichen Schlüssel den privaten Schlüssel zu berechnen, und es darf nur mit Hilfe des geheimen Schlüssels möglich sein, die Nachricht zu entschlüsseln.

Funktionen, bei denen es (praktisch) unmöglich ist, aus dem Bild das Urbild zu berechnen, nennt man Einwegfunktionen (engl. one-way functions). Kann man das Urbild mit Hilfe ei- nes Geheimnisses doch (effizient) berechnen, so nennt man eine solche Einwegfunktion auch Trapdoor-Funktion. Solche Funktionen suchen wir, um Public-key Kryptographie betreiben zu

können.

Da viele bekannte Public-Key Kryptosysteme Ergebnisse aus der Algebra und Zahlentheorie verwenden, müssen/dürfen wir Mathematik betreiben.

1.1. Einige Grundlagen der Rechnerarithmetik

Wie wir noch sehen werden, arbeiten viele Verfahren der Public-Key Kryptographie mit großen natürlichen Zahlen mit bis zu 4096 Bit (ca. 1200 Dezimalstellen). Aus diesem Grund bildet eine Bibliothek zum Rechnen mit großen Zahlen die Basis für viele Algorithmen der Public-Key Kryptographie. Die dazu benötigten Algorithmen sollen in diesem Abschnitt kurz vorgestellt werden. Details und Erweiterungen finden sich in [Knu98] und umfassende Informationen zur Implementation gibt [Wel01].

1.1.1. Stellenwertsysteme

Üblicherweise repräsentieren Digitalcomputer natürliche Zahlen in Binärdarstellung einer fester Länge, d.h. eine Zahl wird als geordnete Folge

(x_n−1x_n−2. . .x₁x₀)₂,wobei x_i∈{0, 1} und1⩽i < n,

dargestellt. Die Zahlnwird oftRegisterbreitegenannt. Die Folge(x_n−1x_n−2. . .x₁x₀)₂ repräsen- tiert dann den Wert

x=

n−1∑

i=0

x_i2ⁱ

Das Gewicht der iten Ziffer x_i ist also eine 2er Potenz und2 wird alsBasis des Zahlensystems bezeichnet. Offensichtlich kann man auch andere BasenBfür eine Zahlendarstellung verwenden.

Üblicherweise kommen z.B. noch B = 16 (Hexadezimaldarstellung), B = 10 (Dezimaldarstel- lung), B=8(Oktaldarstellung) oder B=60 (Sexagesimaldarstellung) zum Einsatz.

IstB⩾2 die Basis einer Zahlendarstellung, so nennen wir diese B-näre Darstellung. Der Ein- fachheit halber verwenden wir für den Wert x=∑_n−1

i=0 x_i2ⁱ auch (x_n−1x_n−2. . .x₁x₀)₂, d.h. wir unterscheiden nicht zwischen Wert und der jeweiligen Darstellung der Zahl.

1.1.2. Die klassischen Algorithmen

In diesem Abschnitt sollen die klassischen Algorithmen zur Addition, Subtraktion und Multipli- kation und Division von Zahlen in B-närer Darstellung vorgestellt werden, die üblicherweise für die BasisB=10 verwendet werden.

1.1.2.1. Die Addition und Subtraktion Sei B⩾2 die Basis unserer Zahlendarstellung und a = (a_n−1a_n−2. . .a₁a₀)_B

b = (b_n−1b_n−2. . .b₁b₀)_B

(8)

1. Klassische Public-Key Kryptographie

Algorithmus 1: Addition zweier natürlicher Zahlen

Eingabe : Zwei Zahlena= (a_n−1. . .a₁a₀)_B,b= (b_n−1. . .b₁b₀)_B und die Anzahl der Ziffernn

Ergebnis: Die Summe c= (c_n−1. . .c₁c₀)_B von aund bund einen evtl. Übertrag

/* Initalisiere den Zähler */

i=0;

/* Initalisiere den Übertrag */

carry=0;

for (i=0; i < n; i++){ t=a[i] +b[i] +carry;

c[i] =tmodB;

/* tdivB */

carry=⌊_B^t⌋; }

/* Gebe einen evtl. Überlauf zurück */

return carry;

zwei Zahlen in B-närer Darstellung. Es gilt:

a+b =

n−1∑

i=0

a_iBⁱ+

n−1∑

i=0

b_iBⁱ

=

n−1∑

i=0

(a_i+b_i)Bⁱ

Da die Ziffern ai,bi ∈{0, . . .B−1} sind, gilt 0 ⩽(ai+bi) ⩽2(B−1) für0 ⩽i < n, d.h. die Summe a_i+b_i kann evtl. nicht mehr als einzelne Ziffer dargestellt werden. Offensichtlich ist 2(B−1) =2B−2=1·B¹+ (B−2)·B⁰ = (1B−2)B, d.h. die Summea_i+b_ikann alsB-näre Ziffer plus einem Übertrag von maximal 1 auf die nächste Ziffer darstellt werden.

Damit ergibt sich Algorithmus 1 zur Addition von zwei Zahlen, wenn a und b die gleiche Anzahl von Ziffern haben.

Bemerkung 1:

• Die spezielle Wahl der Basis B hat keinen Einfluß auf Algorithmus 1, d.h. wir wählen B so, dass

– möglichst wenige Schleifendurchläufe benötigt werden und

– der verarbeitende Prozessor die Summe a[i] +b[i] +carry effizient berechnen kann.

Der Übertrag auf eine nächste Ziffer wird üblicherweise mit dem englischen Wort

„carry“ bezeichnet.

• Für32-Bit Prozessoren bietet sichB=2³²an, da diese Wahl dafür sorgt, dass der Prozessor die Summe a[i] +b[i] +carryeffizient mit zwei Maschinenbefehlen berechnen kann.

• Bei einer C-Implementierung bietet es sich an, die Zahlen als Array vom Typ unsigned longabzuspeichern, wobei die erste Arraykomponente die Anzahl der Ziffern der jeweiligen Zahl enthält.

Die Subtraktion kann mit einem sehr ähnlichen Algorithmus implementiert werden, wenn a und bdie gleiche Anzahl von Ziffern hat (siehe Algorithmus2).

Beispiel 2: Sei B = 10. Dann ergeben sich bei der Berechnung von 1372−1285 = 0087 mit Algorithmus 2 die folgenden Zwischenwerte:

(9)

1.1. Einige Grundlagen der Rechnerarithmetik

Algorithmus 2: Subtraktion zweier natürlicher Zahlen

Ergebnis: Die Differenz c= (c_n−1. . .c₁c₀)B von aund bund einen evtl. Unterlauf

/* Initalisiere den Zähler */

i=0;

/* borrow==1, wenn von der aktuellen Stelle nicht geborgt wurde */

borrow=1;

for (i=0; i < n; i++){ if (borrow==1){

t=B+a[i] −b[i];

} else{

t= (B−1) +a[i] −b[i];

}

c[i] =tmodB;

/* tdivB */

borrow=⌊_B^t⌋; }

/* Gebe einen evtl. Unterlauf zurück */

return borrow;

i a[i] b[i] t c[i] borrow

0 2 5 7 7 0

1 7 8 8 8 0

2 3 2 10 0 1

3 1 1 10 0 1

Beobachtung 3: Die Algorithmen 1 und 2 haben eine Laufzeit von O(n), wobein die Anzahl der Ziffern der Zahlena und b ist.

1.1.2.2. Die Multiplikation Sei B⩾2 und

a = (a_n−1a_n−2. . .a₁a₀)_B b = (b_n−1b_n−2. . .b₁b₀)B

zwei Zahlen in B-närer Darstellung, dann gilt a·b = (

n−1∑

i=0

a_iBⁱ)·(

n−1∑

i=0

b_iBⁱ)

= b₀·(

n−1∑

i=0

a_iBⁱ) +b₁B¹·(

n−1∑

i=0

a_iBⁱ) +· · ·+b_n−1Bⁿ⁻¹·(

n−1∑

i=0

a_iBⁱ)

=

n−1∑

i=0

aib₀Bⁱ+

n−1∑

i=0

aib₁Bⁱ⁺¹+· · ·+

n−1∑

i=0

aib_n−1B^i+(n−1)

=

n−1∑

j=0 n−1∑

i=0

a_ib_jB^i+j (⋆)

Damit ergibt sich für zwei Zahlenaundbderen DarstellungnZiffern lang ist, dass das Produkt a ·b aus maximal (n −1) + (n− 1) + 1+ 1 = 2n signifikanten Stellen besteht. Für eine

(10)

Algorithmus 3: Multiplikation zweier natürlicher Zahlen

Ergebnis: Das Produkt c= (c_2·_n−1. . .c₁c₀)B von a undb

/* Initalisiere das Ergebnisarray */

for (i=0; i <2·n; i++){ c[i] =0;

}

/* Führe die eigentliche Multiplikation durch */

for (j=0; j < n; j++) { carry=0;

for(i=0; i < n; i++){

t=c[i+j] +a[i]·b[j] +carry;

c[i+j] =tmodB; carry=⌊_B^t⌋; }

c[i+n] =carry;

}

Implementierung ist die Summendarstellung (⋆) nicht effizient nutzbar, da erst die Produkte a_ib_j berechnet und gespeichert werden müssten. Sei c[i+j] die (i+j)te Stelle der Zahl a·b, dann berechnen wir einfacher

t=c[i+j] +a[i]·[j] +carry,

wobeicarryder Übertrag aus der Berechnung der letzten Stelle ist. Da0⩽c[i+j],a[i],b[i], carry⩽ (B−1) ist, gilt0⩽t⩽(B−1) + (B−1)²+ (B−1) =2B−2+B²−2B+1=B²−1und weiterhin

B²−1= (B| {z }−1)

Ziffer

·B¹+ (B| {z }−1)

Ziffer

·B⁰.

Deshalb kanntin zweiB-nären Ziffern gespeichert werden. Die zweite Ziffer vontdient als Über- trag für die nächste Berechnung, d.h. der folgende Algorithmus besteht aus zwei verschachtelten Schleifen, wobei die äußere Schleife die Teilprodukte bj·(a_n−1. . .a₁a₀)_Bberechnet.

Beispiel 4: SeiB=10, a= (123)₁₀ und b= (987)₁₀, dann ista·b= (121401)₁₀, da sich mit Algorithmus 3 folgende Werte ergeben:

j i carry t c[0] c[1] c[2] c[3] c[4] c[5]

0 0 0 21 1 0 0 0 0 0

0 1 2 26 6 0 0 0 0 0

0 2 2 29 1 6 9 2 0 0

1 0 0 20 1 0 9 2 0 0

1 1 2 27 1 0 7 2 0 0

1 2 2 22 1 0 7 2 2 0

2 0 0 14 1 0 4 2 2 0

2 1 1 11 1 0 4 1 2 0

2 2 1 12 1 0 4 1 2 1

(11)

Bemerkung 5:

• Algorithmus3benötigt eine Funktion um zwei Ziffern der BasisBmultiplizieren zu können.

Wählt man B = 2³², so ist die evtl. in C nicht immer direkt möglich (evtl. kein 64 Bit Datentyp auf 32 Bit Rechnern).

• Die Laufzeit dieses Algorithmus ist O(n²). Es existiert ein asymptotisch schnellerer Multi- plikationsalgorithmus mitO(nlognlog logn), der die FFT (Fast Fourier Transformation) benutzt. Allerdings ist hier der Overhead (≜ die Konstante, die durch dieO-Notation ver- borgen wird) extrem groß. Für kryptographische Zwecke ist deshalb derO(n²)-Algorithmus dennoch schneller. Evtl. kann die Karatsuba-Multiplikation mit O(n^log²³) = O(n^1.58496) zum Einsatz kommen.

• Die Wahl der Basis hat starke Auswirkungen auf die Laufzeit. Sei die Laufzeit einer konkreten Implementierung c·n², wobei c eine Konstante ist, dann ergibt sich im Fall B=2³²für(a_n−1. . .a₀)₂32·(b_n−1. . .b₀)₂32 eine Laufzeit vonc·n². Wählt man nunB=2¹⁶ so sind die beiden Zahlen in dieser Darstellung doppelt so lang, d.h. (a_2·^′_n−1. . .a₀^′)₂16

bzw. (b_2·n−1^′ . . .b₀^′)₂16, womit sich eine Laufzeit von c·(2n)² = 4·c·n² ergibt. D.h. das Verdoppeln der Anzahl der Bits der Basis verkleinert die Laufzeit auf ein Viertel.

1.1.2.3. Die Division Im Vergleich zu den Algorithmen für Addition, Subtraktion und Multi- plikation, erzeugt der Divisionsalgorithmus mit Abstand den größten Implementierungsaufwand, was durch seine vergleichsweise komplexe Struktur bedingt ist.

Ab jetzt gehen wir davon aus, dass a > b. Wir suchen also einen Algorithmus der q und 0⩽r < b bestimmt, sodass

a=q·b+r

gilt, d.h. q = ⌊a⌋ und r = amodb. Es kann gezeigt werden, das q und r eindeutig bestimmt sind.

Definition 6: SeiB⩾2 eine beliebige Basis. Wir sagen eine Zahlc= (c_n−1c_n−2. . .c₁c₀)_B ist normalisiert, wennc_n−1⩾⌊^B₂⌋ gilt.

Soll q= ⌊a/b⌋ und r = amodb berechnet werden, dann können a und bmit einer Zahl d so multipliziert werden, dass bnormalisiert ist. Es gilt:

a = qb+r ad = qbd+rd,

d.h. durch die Normalisierung ändert sichqnicht und der berechnete Restrdmuss noch durchd geteilt werden, umrzu enthalten. Ab jetzt gehen wir davon aus, dassbbei der Berechnung von q = ⌊a⌋ und r = amodb schon normalisiert ist, allerdings muss dann berücksichtigt werden, dass aevtl. eine Stelle länger wird:

2n+1Stellen

z }| {

(a_2na_2n−1. . .a₀)_B:

nStellen

z }| { (b_n−1. . .b₀)_B=

nStellen

z }| {

(q_n−1. . .q₀)_B und Rest

nStellen

z }| { (r_n−1. . .r₀).

Soll der klassische Divisionsalgorithmus durchführt werden, so müssen die verschiedenen q_i berechnet oder geraten werden, um dann in jedem Schrittq_i·bvona abziehen zu können. Bei großen Basen ist es also sehr ineffizient qidurch Probieren aller Möglichkeiten zu ermitteln. Sei nun

ˆ

q_i=defmin

(⌊aj+nB+a_j+n−1 b_j−1

⌋ ,B−1

)

(12)

Satz 7: Sei a = (ana_n−1. . .a₀)B und b= (b_n−1. . .b₀)B, wobei b normalisiert, dann gilt bei der Durchführung des Divisionsalgorithmus für q_i, 0⩽i < n:

ˆ

qi−2⩽qi⩽qˆi

Beweis: Siehe [Knu98, Abschnitt 4.3.1, Theorem A und Theorem B]. # Beobachtung 8:

• Die vorläufige Ziffer qˆ_i unterscheidet sich,unabhängig von der Basis, maximal um 2 von der wirklichen Ziffer qi und

• qˆ_i ist nie zu klein.

• Die Wahrscheinlichkeit, dass qˆ_ium 2zu groß ist, beträgt _B². Dies bedeutet aber auch, dass spezielle Tests der Software für diesen Fall benötigt werden.

Mit Hilfe dieser Techniken ergibt sich Algorithmus4.

Beispiel 9: SeiB=10 und n=3. Wir dividieren 723604 durch 203. Es ergeben mit Hilfe von Algorithmus 4 die folgenden Zwischenwerte:

i a₆ a₅ a₄ a₃ a₂ a₁ a₀ b₂ b₁ b₀ qˆ q₃ q₂ q₁ q₀ qbˆ

− 0 7 2 3 6 0 4 2 0 3 − − − − − −

− 2 8 9 4 4 1 6 8 1 2 − − − − − −

3 2 4 3 6 4 1 6 8 1 2 28/8=3 − − − − 3·812=2436

3 0 4 5 8 4 1 6 8 1 2 − 3 − − − −

2 0 4 0 6 0 1 6 8 1 2 45/8=5 3 − − − 5·812=4060

2 0 0 5 2 4 1 6 8 1 2 − 3 5 − − −

1 0 0 4 8 7 2 6 8 1 2 52/8=6 3 5 − − 6·812=4872

1 0 0 0 3 6 9 6 8 1 2 − 3 5 6 − −

0 0 0 0 3 2 4 8 8 1 2 36/8=4 3 5 6 − 4·812=3248

0 0 0 0 0 4 4 8 8 1 2 − 3 5 6 4 −

− 0 0 0 0 1 1 2 8 1 2 − 3 5 6 4 −

Somit erhalten wir den Quotienten q= (3564)₁₀ und den Rest r= (0112)₁₀

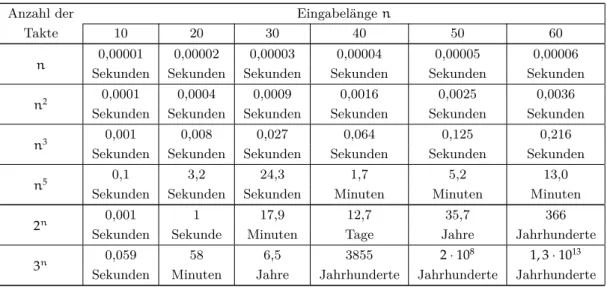
Damit zeigt sich, dass effiziente Algorithmen für die Addition, Subtraktion, Multiplikation und Division von natürlichen bzw. ganzen Zahlen existieren. Ein Algorithmus heißt dabei effizient, wenn seine Laufzeit durch ein Polynom p(n) beschränkt ist, wobei n die Anzahl der Bits ist, die gebraucht werden, um die Eingabe zu kodieren (siehe Abbildung 1). Es ergeben sich die folgenden Laufzeiten für die klassischen Algorithmen:

• Addition / Subtraktion: O(n)

• Multiplikation / Division: O(n²)mit der „Schulmethode“

(13)

Algorithmus 4: Division zweier natürlicher Zahlen

Eingabe : Zwei Zahlena^′ = (a_2n−1^′ . . .a₁^′a₀^′)B,b^′(b_n−1^′ . . .b₁^′b₀^′)B und die Anzahlnder Ziffern des Divisors

Ergebnis: Der Quotient q= (q_n−1. . .q₁q₀)_B und der Restr= (r_n−1. . .r₁r₀)_B, so dass a^′=qb^′+r

berechne den Normalisierungsfaktor d;

(a_2n. . .a₁a₀)_B=a^′·d;

(b_n−1. . .b₁b₀)B=b^′·d;

for (i⩽n; i⩽0;i++) { ˆ

q=min(⌊^aⁱ⁺ⁿ^B+a_b_n−1ⁱ⁺ⁿ⁻¹⌋,B−1);

seia_neu = (ai+n. . .ai)B−qˆ ·(b_n−1. . .b₀)B;

/* qˆ zu groß */

if (a_neu<0) {

a_neu=a_neu+ (b_n−1. . .b₀)B; q–;ˆ

}

/* qˆ immer noch zu groß (sehr selten) */

if (a_neu<0) {

a_neu=a_neu+ (b_n−1. . .b₀)_B; q–;ˆ

}

ersetze(ai+n. . .ai) durchaneu; q_i=q;ˆ

}

denormalisiere r;

return r undq;

Anzahl der Objekten

Instruktionen 10 20 30 40 50 60

0.00001 0.00002 0.00003 0.00004 0.00005 0.00006

n Sekunden Sekunden Sekunden Sekunden Sekunden Sekunden

0.0001 0.0004 0.0009 0.0016 0.0025 0.0036

n²

Sekunden Sekunden Sekunden Sekunden Sekunden Sekunden

0.001 0.008 0.027 0.064 0.125 0.216

n³

Sekunden Sekunden Sekunden Sekunden Sekunden Sekunden

0.1 3,2 24.3 1.7 5.2 13.0

n⁵

Sekunden Sekunden Sekunden Minuten Minuten Minuten

0.001 1 17.9 12.7 35.7 366

2ⁿ

Sekunden Sekunde Minuten Tage Jahre Jahrhunderte

0.059 58 6.5 3855 2·10⁸ 1.3·10¹³

3ⁿ

Sekunden Minuten Jahre Jahrhunderte Jahrhunderte Jahrhunderte

Abbildung 1: Rechenzeitbedarf von Algorithmen auf einem „1-MIPS“-Rechner

(14)

Algorithmus 5: Exponentiation zweier natürlicher Zahlen Eingabe : Zwei Zahlenx= (x_n−1. . .x₁x₀)_B,e= (e_n−1. . .e₁e₀)_B Ergebnis:x^e

/* Initalisiere temporäre Variable */

y=x;

/* Arbeite alle Bits der Binärdarstellung von e ab */

for (i=BitLength(e) −2; i⩾0;i–) { y=y²·x^Bit(e,i);

}

return y;

1.1.2.4. Die Exponentiation Offensichtlich ist die triviale Methode a^b = a| ·a·a{z·. . .·a}

b−mal

zu langsam, denn dieser Algorithmus braucht O(2ⁿ) Multiplikationen. Dies ist also kein effizienter Algorithmus. Die folgende Idee führt zum Ziel: Füra²ⁿ berechne

( . . .((

a²)2)···)2

,

wobei genau n-mal quadriert wird. D.h. für a¹⁶ benötigen wir nur 4 Multiplikationen statt 16 Multiplikationen bei der naiven Methode.

Es stellt sich die Frage, wie wir dieses Vorgehen für Zahlen anwenden, die keine Zweierpotenz sind. Da jede natürliche Zahl als Summe von Zweierpotenzen (Binärdarstellung) geschrieben werden kann, ergibt sich füre∈N:

e = 2ⁿ⁻¹e_n−1+2ⁿ⁻²e_n−2+· · ·+2¹e₁+2⁰e₀, mite_n−1=1

= (2ⁿ⁻²e_n−1+2ⁿ⁻³e_n−2+· · ·+2⁰e₁)·2+e₀ ... (vergleiche „Horner-Schema“)

= (. . .((2e_n−1+e_n−2)·2+e_n−3)·2+. . .+e₁)·2+e₀, Dann ergibt sich

x^e = x^(...((2eⁿ⁻¹^+eⁿ⁻²^)·2+eⁿ⁻³^{)·2+···+e}¹^)·2+e⁰

= (

x^(...((2eⁿ⁻¹^+eⁿ⁻²⁾^·2+eⁿ⁻³⁾^·2+^···^+e¹⁾)2

·x^e⁰ ... (mit e_n−1=1)

= (

. . .((

x²·x^eⁿ⁻²)2

·x^eⁿ⁻³ )₂

·. . . )₂

·x^e⁰.

D.h. wir benötigen n−1 Schritte, umx^e zu berechnen. Diese Methode zur Potenzierung heißt

„Repeated square-and-multiply“ (siehe Algorithmus 5). Offensichtlich beträgt die Laufzeit von Algorithmus5 dann O(n³).

1.2. Einige Grundlagen aus der elementaren Zahlentheorie

Z ist das Symbol für die geordnete Menge {. . . ,−3,−2,−1, 0, 1, 2, 3, . . .} der ganzen Zahlen und N das Symbol für die Menge dernatürlichen Zahlen {0, 1, 2, 3, . . .}.

Bekannt ist, dass Z mit der normalen Zahlenaddition und -multiplikation ein kommutativer Ring mit Einselement ist.

(15)

1.2. Einige Grundlagen aus der elementaren Zahlentheorie

1.2.1. Der größte gemeinsame Teiler

Definition 10: Wir sagen ateilt n(kurz:a|n), wenn es eine ganze Zahl bgibt mitn=a·b.

Teilta nichtn, so schreibt man kurz a∤n.

Satz 11: Seien a,b,c∈Z, dann gilt:

(i) Aus a|b und b|c folgt a|c.

(ii) Aus a|b folgtac|bcfür alle c.

(iii) Aus c|a und c|bfolgt c|(da+eb) für alle d∈Z und e∈Z. (iv) Aus a|b und b̸=0 folgt |a|⩽|b|.

(v) Aus a|b und b|a folgt |a|=|b|.

Beweis: Übungsaufgabe! #

Definition 12: Ein gemeinsamer Teiler von aund bist eine ganze Zahl d mit d|a und d|b.

Beobachtung 13: Gilt nicht a=b=0, dann gibt es einen größten gemeinsamen Teilervon a und b (kurz:ggT(a,b)), denn die Teiler von a (bzw.b) sind durch |a| (bzw. |b|) beschränkt.

Definition 14: Ist ggT(a,b) =1, so heißt a (relativ) primzu b, a is coprim zu b oder a und b sind teilerfremd.

Satz 15 (Lineardarstellung des ggTs): Seien x,y∈Z und nicht x= y= 0, dann existiert a,b∈Zmit

ax+by=ggT(x,y).

Beweis: Sei g > 0 die kleinste positive ganze Zahl der Form ax+by mit a,b∈ Z. (Eine Zahl solcher Form gibt es, z.B.x²+y².)

Wir zeigen, dassg=ggT(x,y)gilt. Jeder gemeinsame Teiler vonxundyteilt auchg=ax+by (siehe Satz 11(iii)), also insbesondereggT(x,y)|g. Angenommeng∤x, dann ist x=tg+r mit t,r∈Zund0< r < g. Also istr=x−tg=x−t(ax+bx) =x−tax−tby= (1−ta)x+ (−tb)y, und dies ist ein Widerspruch zur Minimalität von g (denn r < g), also g| x. Analog lässt sich zeigen, dass g|y.

Damit ist g ein gemeinsamer Teiler von x und y, also ist der ggT(x,y) ein Vielfaches von g und g|ggT(x,y). Mit Punkt Satz 11(v) des letzten Satzes folgt dann g=ggT(x,y). #

Nun stellt sich die Frage, wie man den ggT (effizient) berechnet. Dazu verwenden wir den Euklidischen Algorithmus. Wenn n,m ∈ Z und m ̸= 0, dann können wir n durch m teilen (eventuell mit Rest) und es gilt n=q·m+rmit0⩽r <|m|, wobei diese Darstellung eindeutig

ist. Der Rest rwird kurz mit „amodb“ notiert, und der Quotientqmit „adivb“.

Algorithmus 6 terminiert, weil r ⩾ 0 und r in jedem Schleifendurchlauf kleiner wird (da amodb < b). Weiterhin gilt ggT(x,y) =ggT(y,xmody) als Schleifeninvariante, was die Kor- rektheit des Algorithmus zeigt (siehe [Knu98, Seite 337]). Dann stellt sich die Frage, ob es einen Algorithmus gibt, der die Lineardarstellung des ggT ausrechnet. Ein solcher Algorithmus ist als erweiterter Euklidische Algorithmusbekannt.

(16)

Algorithmus 6: Euklidischer Algorithmus Eingabe :a,b∈N

Ergebnis: Der größte gemeinsame Teiler von aund b while(b̸=0){

r=amodb;

a=b;

b=r;

}

/* Gebe den ggT zurück */

return b;

Seienx,y∈N, dann wird derggT durch die folgenden Schritte berechnet, wobeir₀=def xund r₁ =defy.

r₀ = q₁r₁+r₂, 0< r₂ < r₁ r₁ = q₂r₂+r₃, 0< r₃ < r₂

...

r_k−1 = q_kr_k+r_k+1, 0< r_k+1 < r_k ...

r_n−2 = q_n−1r_n−1+r_n, 0< r_n< r_n−1 r_n−1 = q_nr_n+r_n+1

| {z }

=0

.

Der ggT vonx undyist dann r_n und diese Berechnung terminiert, weil r₁> r₂ > r₃>· · ·⩾0.

Satz 16: Sei nun x,y∈N, dann (i) rn=ggT(x,y).

(ii) Es istggT(x,y) =ax+by, wobei die Koeffizientena und bmit dem Erweiterten Euklidi- schen Algorithmus berechnet werden können.

Beweis:

Sei nun t irgendein gemeinsamer Teiler von x und y, dann folgt aus obigen Gleichungen:

t|rk fürk=1, 2, . . .und insbesondere t|rn, d.h.rn muss der ggT sein.

(ii) Wir substituieren iterativ r_k+1 durchr_k−1−q_kr_k, d.h.

rn = r_n−2−q_n−1r_n−1

= r_n−2−q_n−1(r_n−3−q_n−2r_n−2)

= (1+q_n−1q_n−2)r_n−2−q_n−1r_n−3 ...

= ax+by mita,b∈Z.

#

(17)

1.2. Einige Grundlagen aus der elementaren Zahlentheorie

1.2.2. Restklassenringe

Sein∈N\{0}unda,b∈Z, dann istakongruentbmodulon(kurz:a≡bmodnodera≡b(n)), wenn n | (b−a). Dabei ist „≡“ eine Äquivalenzrelation, und a =def {b | b ≡ amodn} ist die Äquivalenzklasse aller zua kongruenten Zahlen. Für die Äquivalenzklasse anennt man aauch einen Repräsentantenoder Vertreter undaRestklasse(modulon). Die Menge aller Restklassen {a|a∈Z} modulon wird mitZn bezeichnet.

Offensichtlich ist jedes a ∈Z kongruent zu einer Zahl 0 ⩽r < n, d.h. die Zahlen 0⩽ r < n sind Repräsentanten für alle Restklassen inZn. Sie heißen auch dienatürlichen Repräsentanten.

Da füra≡a^′(n) undb≡b^′ (n)gilt: a+b≡a^′+b^′ (n)unda·b≡a^′·b^′ (n), ist(Zn,+,·) ein kommutativer Ring mit Einselement.

Oft schreiben wir a statt a und benutzen den Repräsentanten der Klasse. Hat a ∈ Zn ein multiplikativ Inverses, also gibt es ein b ∈ Zn mit ab ≡ 1 (n), dann nennen wir a prime Restklasse,Einheit oder Unit).

Satz 17: Sei n⩾2, dann ista eine Einheit genau dann, wenn ggT(a,n) =1.

Beweis:

„⇒“ Sei aprime Restklasse, also existiert ein bmitab≡1 modn, dann gilt n|(1−ab) und nach Definition von „|“ folgt nm+ab = 1. Nun muss ggT(a,n) = 1 gelten, denn sonst könnte ein g⩾2aus der Summe nm+abausgeklammert werden.

„⇐“ Es seiggT(a,n) =1, also existierene,d∈Zmitae+nd=1. Dann gilt1−ae=ndund n|(1−ae). Also ist ae≡1 modnund damit ist a eine prime Restklasse. # Definition 18: Sei n⩾2, dann ist

Z^∗_n=def{a| 1⩽a⩽n−1 und ggT(a,n) =1}

die Einheitengruppe von Zn (d.h. (Z^∗n,·) ist eine endliche Gruppe). Sei ϕ(n) =def#(Z^∗n), dann ist ϕ(n) also die Anzahl der natürlichen Zahlen aus der Menge {1, . . . ,n−1}, die zu n relativ prim sind. ϕ heißt die Eulersche Phi-Funktion (engl. Euler’s totient function).

Folgerung 19: (Zn,+,·) ist endlicher Körper gdw. n∈P.

Beweis: Übungsaufgabe #

Satz 20 (Satz von Euler): Seien a∈N\ {0},n⩾2 und ggT(a,n) =1, dann gilt a^ϕ(n)≡1 modn.

Beweis: Sei Z^∗n={a₁, . . . ,a_ϕ(n)}, dann ist

a^ϕ(n)·a₁·a₂·. . .·a_ϕ(n) ≡ aa₁·aa₂·. . .·aa_ϕ(n)modn

≡ a_π(1)·a_π(2)·. . .·a_π(ϕ(n))modn(π ist eine Permutation)

≡ a₁·a₂·. . .·a_ϕ(n)modn.

Da(Z^∗n,·)eine Gruppe ist, muss a^ϕ(n)≡1 modngelten. # Folgerung 21 (Kleiner Satz von Fermat): Sei p Primzahl, dann gilt füra̸=0 modp

a^p−1 ≡1 modp.

Beweis: Ist pprim, so gilt ϕ(p) =p−1. Die Aussage ergibt sich dann direkt aus dem Satz von

Euler (Satz 20). #

(18)

Bemerkung 22: Eine alternative (leicht verbesserte) Form des kleinen Satzes von Fermat ist:

Ist pprim, dann a^p≡amodp.

Lemma 23: Sei k⩾1 und p∈Nprim, dann gilt ϕ(p^k) =p^k−1(p−1).

Beweis: Übungsaufgabe #

Satz 24 (vgl. [HW80]): Sei n∈Nund n=p^e₁¹·. . .·p^e_r^r mitp_i∈P, p_i̸=p_j wenni̸=j und 1⩽i⩽r. Dann gilt:

ϕ(n) =n

∏r i=1

( 1− 1

pi

) .

Für m=p·q und p,q∈Pgilt also insbesondere ϕ(m) = (p−1)(q−1).

Beweis: Sei ggT(n,m) =1, dann ist ϕ(nm) =ϕ(n)·ϕ(m). Dazu zeigen wir zunächst: Wenn a alle Werte zwischen 0 und n−1 annimmt und a^′ alle Werte zwischen 0 und m−1 annimmt, dann durchläufta^′n+amalle RestklassenZmn.

Es gibtnmverschiedene Zahlen a^′n+amund falls a₁^′n+a₁m≡a₂^′n+a₂mmodnm, dann ist a₁^′n ≡ a₂^′nmodm und a₁m ≡ a₂mmodn. Damit ergibt sich a₁^′ ≡ a₂^′modm und a₁ ≡ a₂modn, da die jeweiligen inversen Elemente vonnbzw.minZm bzw.Znexistieren. D.h. die nmverschiedenen Zahlena^′n+amsind inkongruent und es werden alle Restklassen durchlaufen.

Nun ist

ggT(a^′n+am,nm) =1 gdw. ggT(a^′n+am,m) =1 und ggT(a^′n+am,n) =1 gdw. ggT(a^′n,m) =1und ggT(am,n) =1

gdw. ggT(a^′,m) =1 undggT(a,n) =1.

Zu jedem zu nm coprimen Rest aus Znm ist also genau ein Paar von zu n bzw. m coprimen Resten zugeordnet. Also gilt auchϕ(nm) =ϕ(n)·ϕ(m). Damit ist die anfängliche Behauptung bewiesen.

Da fürpi,pj ∈Pmitpi̸=pj und ei,ej ∈N trivialerweiseggT(p^e_iⁱ,p^e_j^j) =1 gilt, folgt:

ϕ(n) = ϕ(p^e₁¹ ·. . .·p^e_r^r)

= ϕ(p^e₁¹)·. . .·ϕ(p^e_r^r)

= p^e₁¹⁻¹(p₁−1)·. . .·p^e_r^r⁻¹(p_r−1)

= n·( 1− _p¹

1

)·. . .·( 1− _p¹

r

)

= n· ∏^r

i=1

( 1−_p¹

i

)

Die zweite Aussage folgt dann offensichtlich. #

1.3. Das RSA Public-Key Kryptosystem

Dieses Verfahren wurde 1978 von R. Rivest, A. Shamir und L. Adleman in der Arbeit „A Method for Obtaining Digital Signatures and Public-Key Cryptosystems“ eingeführt¹und ist auch heute noch im Gebrauch.

1.3.1. RSA – Schlüsselerzeugung

Die Schlüsselerzeugung für das RSA-Verfahren geschieht in drei Schritten:

1. Wähle zwei unterschiedliche Primzahlenp undq und berechnen=p·q.

1Angeblich wurde ein vergleichbares asymmetrisches Verschlüsselungsverfahren schon früher durch die britische Behörde CESG entdeckt (siehe [Ell87]).

(19)

1.3. Das RSA Public-Key Kryptosystem

2. Wähle eine∈Z^∗_ϕ(n), wobeiϕ(n) = (p−1)(q−1).

3. Berechne ein d∈Z^∗_ϕ(n) mited≡1 modϕ(n).

Es ergibt sich:

Public Key: (e,n) Private Key:(d,n) Bemerkung 25:

Zu 1: Zum jetzigen Zeitpunkt müssen die Primzahlenpund qmindestens512Bit groß sein. Es stellt sich also die Frage, wie diese Primzahlen berechnet werden können.

Zu 2: Wir wählen ein zufälliges 2⩽e⩽ϕ(n) −1 und prüfen, ob ggT(e,ϕ(n)) =1 via Euklidi- schem Algorithmus.

Zu 3: Wir wissen schon 1 = ggT(e,ϕ(n)) = ed+ϕ(n)n^′ (siehe Satz 16). Damit gilt 1 ≡ edmodϕ(n), d.h. wir berechnen den geheimen Schlüsselanteil mit Hilfe des erweiterten Euklidischen Algorithmus.

Bemerkung 26: Die Primzahlenp und q, sowie ϕ(n) müssen geheim bleiben!

• Kennt Erichϕ(n)undnkann ernfaktorisieren (in Primfaktoren zerlegen) und er kann aus edann auchdberechnen. Dann kann er auchp+qberechnen, dennϕ(n) = (p−1)(q−1) = pq−p−q+1=n− (p+q) +1 und p+q=n−ϕ(n) +1. Weiterhin kann Erich auch p−qermitteln, indem er (p+q)²−4n= (p−q)² ausnutzt und p−q=√

(p+q)²−4n (o.B.d.A. p > q) berechnet. Dann ergibt sich 2p= (p+q) + (p−q).

• Das Faktorisierungsproblem ist algorithmisch schwer (d.h. es ist kein Polynomialzeitalgo- rithmus bekannt).

Satz 27 (Chinesischer Restsatz, CRT - Chinese Remainder Theorem): Seien die Zah- len m₁, . . . ,mn paarweise teilerfremd und a₁, . . . ,an∈Z, dann hat die simultane Kongruenz

x ≡ a₁modm₁, x ≡ a₂modm₂,

...

x ≡ a_nmodm_n eine Lösung, die modulo m=

∏n i=1

m_i eindeutig ist.

Beweis: Um die Richtigkeit des Chinesischen Restsatzes zu beweisen, müssen sowohl die Existenz einer Lösung als auch die Eindeutigkeit dieser Lösung gezeigt werden:

„Existenz“: Seim=∏_n

i=1m_iundM_i=m/m_ifür1⩽i⩽n, dann gilt auchggT(mi,M_i) =1, weil allemi paarweise teilerfremd sind.

Wir berechnen das Inversey_ivonM_iinZmi(etwa via Euklidischen Algorithmus), d.h.y_iM_i≡ 1 modmi und setzen x=∑_n

i=1aiyiMimodm(⋆).

Offensichtlich ist xeine Lösung jeder einzelnen Kongruenz, denn x≡aiy| {z }iMi

≡1

+

∑n

j=1 j̸=i

ajyjMj

| {z }

≡0

≡aimodmi.

Damit ist die Existenz gezeigt.

(20)

„Eindeutigkeit“: Angenommen es gibt mehr als eine Lösung, etwazund z^′ (zund z^′ verschieden), dann giltz≡z^′modm_i für1⩽i⩽n. Da diem_i paarweise teilerfremd sind, liefert die Konstruktion (siehe(⋆)), die die Existenz einer Lösung garantiert, auchz≡z^′modm.

Dies ist ein Widerspruch. #

1.3.2. RSA – Ver- und Entschlüsselung

Die Ver- und Entschlüsselung mit Hilfe des RSA-Verfahrens funktioniert dann wie folgt:

E:Zn→Zn mit E(x) =x^emodn D:Zn→Zn mit D(x) =x^dmodn

D.h. die zu verschlüsselnden Nachrichten stammen aus der Menge{0, . . . ,n−1}.

Satz 28: Sei E die RSA-Verschlüsselungsfunktion und D die dazu passende Entschlüsselungs- funktion, dann gilt:

E◦D = D◦E = id.

Beweis: Wir müssen zeigen: x^ed ≡xmodnfür alle x∈Zn.

Fall x∈Z^∗n: Wir wissened−kϕ(n) =1, da ϕ(n)|(ed−1), alsoed=1+kϕ(n) und damit:

x^ed ≡ x^1+kϕ(n)≡x·( x| {z }^ϕ(n)

≡1„Euler“

)^k ≡ xmodn.

Fall x̸∈Z^∗_n: Wenn p | x und q | x, dann x ≡ 0 modn und damit x^ed ≡ xmodn. O.B.d.A.

sei nun p | x und q ∤ x, also xêd ≡ xmodp, weil x ≡ 0 modp, und analog zum obigen xêd ≡xmodq, weil 1 = ed−kϕ(n) = ed−k(p−1)(q−1) = ed−k(p−1)ϕ(q). Also insgesamtxêd ≡(xê)^d ≡xmodn.

Offensichtlich können wir die Rollen des öffentlichen Exponenteneund des privaten Exponenten

d vertauschen, was auchD◦E=id zeigt. #

Bemerkung 29:

• Wir können den „Repeated square-and-multiply“ Algorithmus leicht so anpassen, dass er x^emodn effizient berechnet.

• d sollte größer sein als n^1/4, denn sonst gibt es einen effizienten Algorithmus, um d aus dem öffentlichen Anteil zu berechnen.

• Die Entschlüsselung des Ciphertextes kann mit Hilfe des „Chinesischen Restsatzes“ be- schleunigt werden.

1.4. Digitale Signaturen

Das RSA-System kann zusammen mit Hashfunktionen für digitale Signaturen eingesetzt werden.

Erzeugung: Alice möchte eine Nachrichtm digital signieren.

• Alice berechnet v=h(m) den Hashwert vonm.

• Alice berechnet s≡v^dmodn, wobei0⩽v < n und (d,n) ihr RSA private Key ist.

Überprüfung: Bob möchte überprüfen, ob die Signatur korrekt ist.

• Bob verwendet den public Key(e,n)von Alice.

• Bob berechnet v^′≡s^emodnund h(m).

• Bob akzeptiert die Signatur gdw.v^′=h(m).

(21)

1.5. Angriffe auf RSA

1.5. Angriffe auf RSA

Die Hauptangriffsmöglichkeit auf das RSA-Verfahren ist ein Algorithmus für das folgende Pro- blem:

Problem: FACTORING Eingabe: N∈N

Ausgabe: Größter Primfaktor vonN

Keiner der heute bekannten Algorithmen kann das Faktorisierungsproblem in Polynomialzeit lösen. Sei

L_N(γ,c) =defe^c(logN)^γ^{(log log}^N)^1−γ,

dann sind die schnellsten Methoden deren Laufzeit von der ZahlNabhängt:

• Continued Fraction Method: vermutete Laufzeit O(L_N(¹₂,c₁)),

• Multiple Polynomial Quadratic Sieve: vermutete Laufzeit O(L_N(¹₂,c₂))und

• Number Field Sieve: vermutete Laufzeit O(LN(¹₃,c₃)).

Weiterhin sind Methoden bekannt, deren Laufzeit vom gefundenen Faktorpabhängt:

• Faktorisieren durch Probieren: Laufzeit O(p·(logN)²) und

• Elliptic Curve Method: vermutete Laufzeit O(Lp(¹₂,c₄)·(logN)²).

Bemerkung 30:

• Ein Faktorisierungsalgorithmus mit Laufzeit LN(0,c) ist ein Polynomialzeitalgorithmus, wogegen einL_N(1,c)-Algorithmus exponentielle Laufzeit hat. (Bezogen auf die Eingabelän- ge, alsologN.)

• Nach dem heutigen Stand muss N mindestens 1024 Bit (besser 1536 oder 2048 Bit) lang sein, damit es praktisch nicht faktorisiert werden kann.

Neben der Faktorisierung des öffentlichen Modulus sind noch andere Angriffe auf das RSA- Verfahren bekannt:

Common Modulus Attacke: Angenommen Bob und Bridget haben den öffentlichen Schlüssel (e₁,n)bzw.(e₂,n)und²ggT(e₁,e₂) =1. Seim∈Zndie Nachricht, die an Bob und Bridget geschickt wird. Also gilt c_i ≡m^eⁱmodn für i= 1, 2. Erich berechnet nun re₁+se₂ = 1 und o.B.d.A. gilt r <0.

Fall c₁̸∈Z^∗n: Dann kann ndurch die Berechnung von ggT(c₁,n)>1 faktorisiert werden und alle Parameter sind bekannt.

Fall c₁∈Z^∗n: Berechnec⁻¹₁ ∈Z^∗n, dann gilt

(c⁻¹₁ )^−r·c^s₂ ≡(mê¹)^r·(mê²)^s≡mê¹^r+e²^s ≡mmodn.

Damit kann Erich die Nachricht mberechnen.

Small-Message-Space Attacke: Ist die Zahl der möglichen Nachrichten klein, kann Erich leicht alle Paare von Plain- und Ciphertext ausrechnen, etwa(p₁,c₁),(p₂,c₂), . . .und damit Nach- richten entschlüsseln.

2Dies ist nicht unrealistisch, da die Wahrscheinlichkeit, dass zwei zufällig gewählte natürliche Zahlen relativ prim sind, 6/π²≈0.608beträgt.

(22)

1.6. Primzahlerzeugung

Bei der Erzeugung von RSA-Schlüsseln werden (große) Primzahlen benötigt. Damit stellt sich die Frage, wie diese Primzahlen gefunden werden können.

Satz 31 (Euklid): Es gibt unendlich viele Primzahlen

Beweis: Angenommen es gibt nur endlich viele Primzahlen, etwa p₁, . . . ,pr. Sei n=def 1+p₁· p₂·. . .·pr. Dann giltp_i∤nfür alle 1⩽i⩽r, d.h.n ist entweder eine Primzahl odern enthält neue Primfaktoren, die von allen p_i verschieden sind. Damit ergibt sich ein Widerspruch, was

zeigt, dass es unendlich viele Primzahlen gibt. #

Definition 32: Die Funktion

π(x) =def#{p∈P|p⩽x}

wird Primzahlfunktion genannt und gibt die Anzahl der Primzahlen kleiner gleich xan.

Der folgende Satz wurde schon durch den jungen Gauss vermutet und dann sowohl von Had- amard und de la Vallée Poussin unabhängig bewiesen:

Satz 33: Wenn xgroß ist, dann gilt:

π(x)≈ x ln(x).

Beweis: Sprengt den Rahmen dieser Vorlesung, siehe [HW80] oder eine Vorlesung über Zahlen-

theorie. #

Folgerung 34: Wenn xsehr groß ist, dann ist im Schnitt jede ln(x)-te Zahl eine Primzahl.

Beispiel 35: Es gilt z.B. π(10⁵) =9592 (entdeckt 1668) undπ(10⁶) =78498.

Bemerkung 36: Sei x= 2⁵¹², dann ist ln(x) ≈ 355, d.h. wir müssen im Schnitt 178 Zahlen untersuchen, bis eine Primzahl gefunden ist. Es stellt sich noch die Frage, welche Verfahren / Algorithmen hier zu Einsatz kommen müssen.

Der kleine Satz von Fermat liefert eine notwendige Bedingung für Primzahlen. Sei n ∈ N ungerade und n⩾ 3. Ist n∈ P und a ∈N\ {0} mitggT(a,n) =1, dann ist aⁿ⁻¹ ≡1 modn.

D.h. ist aⁿ⁻¹ ̸≡1 modn, dann giltn̸∈P. Leider ist die Umkehrung der Aussage nicht wahr!

Definition 37: Sei n∈N, n⩾3 und n̸∈P. Wir nennen n eine Carmichael-Zahl, wenn gilt:

aⁿ⁻¹ ≡1 modn für alle a∈N mit ggT(a,n) =1.

Bemerkung 38:

• Die kleinste Carmichael-Zahl ist 561=3·11·17.

• Es gibt unendlich viele Carmichael-Zahlen.

• Jeder Primfaktor einer Carmichael-Zahl kommt nur einmal vor („quadratfrei“).

Aufgrund der Existenz von Carmichael-Zahlen, brauchen wir bessere Verfahren um Primzahlen zu erkennen.

Definition 39: Sei n∈ N und x∈Z, dann heißt x quadratischer Rest modulon, falls es ein y∈Z gibt mit y²≡xmodn. Sonst heißt x quadratischer Nichtrest.

(23)

1.6. Primzahlerzeugung

Definition 40: Sei p eine ungerade Primzahl und a∈Z, dann ist das Legendre-Symbol (

a p

) wie folgt definiert:

(a p

)

=def





0, falls p|a,

+1, falls a quadratischer Rest modulop,

−1, falls a quadratischer Nichtrest modulop.

Sei n ⩾ 3 eine ungerade Zahl mit Primfaktorzerlegung n = pê₁¹pê₂² ·. . .·pê_r^r, dann ist das Jacobi-Symbol (_a

n

) wie folgt definiert:

(a n )

=def

(a p₁

)e₁( a p₂

)e₂

·. . .· ( a

pr

)er

| {z }

Legendre-Symbole

Bemerkung 41: Es existieren Algorithmen, mit denen das Legendre- bzw. Jacobi-Symbol effi- zient berechnet werden kann (vgl. Quadratisches Reziprozitätsgesetzund Ergänzungssätze).

Satz 42: Sei p∈P, dann existiert ein g∈Z^∗_p, sodass Z^∗_p={g⁰,g¹, . . . ,g^p−2}, wobei g⁰=1.

Beweis: Siehe Vorlesung über Zahlentheorie oder Algebra. #

Bemerkung 43: Gruppen, die von einem Element erzeugt werden, nennt man zyklisch. Das erzeugende Element heißt Generator (der Gruppe).

Beispiel 44: Z^∗₅ ={1, 2, 3, 4}={2⁰, 2¹, 2², 2³}, d.h.2 ist Generator von Z^∗₅. Satz 45 (Euler Kriterium): Sei p∈P, ungerade und seix∈Z, dann gilt

(x p

)

≡x^(p−1)/2modp.

Beweis:

Fall p|x: Beide Seiten sind kongruent 0modulo p.

Fall p∤x: Seigein Generator vonZ^∗p. Betrachte die GleichungX²−1= (X+1)(X−1) =0über dem Körper Zp, dann ist g^(p−1)/2 eine Lösung (kleiner Fermat) und g^(p−1)/2 ≡1 modp oder g^(p−1)/2≡−1 modp. Die Lösungg^(p−1)/2 ≡1 modpscheidet aus, weilgsonst kein Generator von Z^∗_pwäre.

Sei x=g^t, dann ist xquadratischer Rest gdw. es einy∈Zgibt mit x≡y²modp

⇔ x≡g^t≡(g|{z}^t/2

≡y

)²modp

⇔ tgerade.

Weiterhin gilt x^(p−1)/2≡(g^t)^(p−1)/2 ≡(g^(p−1)/2)^t ≡1 modpgdw.tgerade. # Diese Aussage wird eine ähnliche Rolle spielen, wie der kleine Satz von Fermat.

Definition 46: Sei n̸∈P und n ungerade, dann ist En=def{a∈Z^∗_n|(a

n

)̸≡a^(n−1)/2modn}

die Menge der Euler-Zeugen für die nicht-Primität von n.