Doubly Balanced Connected Graph Partitioning ∗

(1)

Doubly Balanced Connected Graph Partitioning ^∗

Saleh Soltan

^†

Mihalis Yannakakis

^‡

Gil Zussman

^§

Abstract

We introduce and study the Doubly Balanced Con- nected graph Partitioning (DBCP) problem: Let G=(V, E) be a connected graph with a weight (supply/demand) function p:V→{−1,+1} satisfying p(V)=P

j∈V p(j)=0. The objective is to partition G into (V₁, V₂) such thatG[V₁] andG[V₂] are connected,

|p(V1)|,|p(V2)|≤cp, and max{^|V_|V¹^|

2|,^|V_|V²^|

1|}≤cs, for some constantsc_pandc_s. WhenGis 2-connected, we show that a solution withc_p=1 andc_s=3 always exists and can be found in polynomial time. Moreover, whenG is 3-connected, we show that there is always a ‘perfect’ solution (a partition with p(V1)=p(V2)=0 and

|V1|=|V2|, if |V|≡0(mod 4)), and it can be found in polynomial time. Our techniques can be extended, with similar results, to the case in which the weights are arbitrary (not necessarily ±1), and to the case that p(V)6=0 and the excess supply/demand should be split evenly. They also apply to the problem of partitioning a graph with two types of nodes into two large connected subgraphs that preserve approximately the proportion of the two types.

1 Introduction

Power Grid Islanding is an effective method to miti- gate cascading failures in power grids [16]. The chal- lenge is to partition the network into smaller connected components, calledislands, such that each island can operate independently for a while. In order for an island to operate, it is necessary that the power supply and demand at that island are almost equal (if the supply and demand are not exactly equal but still

∗This work was supported in part by DTRA grant HDTRA1-13-1-0021, DARPA RADICS under contract #FA- 8750-16-C-0054, funding from the U.S. DOE OE as part of the DOE Grid Modernization Initiative, and NSF under grant CCF-1320654 and CCF-1423100. The work of G.Z. was also supported in part by the Blavatnik ICRC and the BSF. We thank Aliakbar Daemi for his helpful comments during our discussions.

†Department of Electrical Engineering, Columbia Univer- sity. Email: saleh@ee.columbia.edu

‡Department of Computer Science, Columbia University.

Email: mihalis@cs.columbia.edu

§Department of Electrical Engineering, Columbia Univer- sity. Email: gil@ee.columbia.edu

relatively close, load shedding/generation curtailing can be used in order for the island to operate). Equal- ity of supply and demand in an island, however, may not be sufficient for its independent operation. It is also important that the infrastructure in that island has the physical capacity to safely transfer the power from the supply nodes to the demand nodes. When the island is large enough compared to the initial network, it is more likely that it has enough capacity.

This problem has been studied in the power systems community but almost all the algorithms provided in the literature are heuristic methods that have been shown to be effective only by simulations [8, 14–16].

Motivated by this application, we formally introduce and study the Doubly Balanced Connected graph Partitioning (DBCP) problem: Let G=(V, E) be a connected graph with a weight (supply/demand) functionp:V→Zsatisfyingp(V)=P

j∈Vp(j)=0. The objective is to partition V into (V1, V2) such that G[V1] and G[V2] are connected, |p(V1)|,|p(V2)|≤cp, and max{^|V_|V¹^|

2|,^|V_|V²^|

1|}≤cs, for some constantscpandcs. We also consider the case that p(V)6=0, in which the excess supply/demand should be split roughly evenly.

The problem calls for a partition into two connected subgraphs that simultaneously balances two objectives, (1) the supply/demand within each part, and (2) the sizes of the parts. The connected partitioning problem with only the size objective has been studied previously. In the most well-known result, Lov´az and Gyori [9, 13] independently proved, using different methods, that everyk-connected graph can be partitioned intokarbitrarily sized connected subgraphs. However, neither of the proofs is construc- tive, and there are no known polynomial-time algorithms to find such a partition for k>3. For k=2, a linear time algorithm is provided in [17] and for k=3 an O(|V|²) algorithm is provided in [19].¹ The complexity of the problem with the size objective and related optimization problems have been studied in [3, 5, 6] and there are various NP-hardness and inapproximability results. Note that the size of the cut is not of any relevance here (so the extensive literature on finding balanced partitions, not necessarily

1Fork=2, a much simpler approach than the one in [17] is to use thest-numbering [11] for 2-connected graphs.

Downloaded 12/04/21 to 118.70.52.165 Redistribution subject to SIAM license or copyright; see https://epubs.siam.org/page/terms

(2)

connected, that minimize the cut is not relevant.) The objective of balancing the supply/demand alone, when all p(i) are ±1, can also be seen as an extension for the objective of balancing the size (which corresponds to p(i)=1). Our bi-objective problem of balancing both supply/demand and size, can be seen also as an extension of the problem of finding a partition that balances the size for two types of nodes simultaneously: Suppose the nodes of a graph are partitioned into red and blue nodes.

Find a partition of the graph into two large connected subgraphs that splits approximately evenly both the red and the blue nodes.

We now summarize our results and techniques.

Since the power grids are designed to withstand a single failure (“N−1” standard) [1], and therefore 2- connected, our focus is mainly on the graphs that are at least 2-connected. We first, in Section 4, study the connected partitioning problem with only the supply/demand balancing objective, and show results that parallel the results for balancing size alone, using similar techniques: The problem is NP-hard in general. For 2-connected graphs and weights p(i)=

±1, there is always a perfectly balanced partition and we can find it easily using anst-numbering. For 3-connected graphs and weights p(i)=±1, there is a perfectly balanced partition into three connected graphs, and we can find it using a nonseparating ear decomposition of 3-connected graphs [4] and similar ideas as in [19].

The problem is more challenging when we deal with both balancing objectives, supply/demand and size. This is the main focus and occupies the bulk of this paper. Our main results are existence results and algorithms for 2- and 3-connected graphs. It is easy to observe that we cannot achieve perfection in one objective (c_p=0 orc_s=1) without sacrificing completely the other objective. We show that allowing the supply/demand of the parts to be off balance by at most the weight of one node suffices to get a partition that is roughly balanced also with respect to size.

First, in Section 4.1, we study the case of 3- connected graphs since we use this later as the ba- sis of handling 2-connected graphs. We show that if ∀i, p(i)=±1, there is a partition that is perfectly balanced with respect to both objectives, if

|V|≡0(mod 4) (otherwise the sizes are slightly off for parity reasons); for general p, the partition is perfect in both objectives up to the weight of a single node. Furthermore, the partition can be constructed in polynomial time. Our approach uses the convex embedding characterization ofk-connectivity studied by Linial, Lov´az, and Wigderson [12]. We need to adapt it for our purposes so that the convex embed-

ding also has certain desired geometric properties, and for this purpose we use the nonseparating ear decomposition of 3-connected graphs of [4] to obtain a suitable embedding.

Then, in Section 4.2, we analyze the case of 2- connected graphs. We reduce it to two subcases:

either (1) there is a separation pair that splits the graph into components that are not very large, or (2) we can perform a series of contractions to achieve a 3-connected graph whose edges represent contracted subgraphs that are not too large. We provide a good partitioning algorithm for case (1), and for case (2) we extend the algorithms for 3-connected graphs to handle also the complications arising from edges representing contracted subgraphs. Finally, in Section 5, we briefly discuss the problem of finding a connected partitioning of a graph with two types of nodes that splits roughly evenly both types.

2 Definitions and Background

In this section, we provide a short overview of the definitions, notation, and tools used in our work.

Most of the graph theoretical terms used in this paper are relatively standard and borrowed from [2]

and [20]. All the graphs in this paper are loopless.

2.1 Terms from Graph Theory Cutpoints and Subgraphs: A cutpoint of a connected graph Gis a node whose deletion results in a disconnected graph. Let X and Y be subsets of the nodes of a graph G. G[X] denotes the subgraph of G induced by X. We denote by E[X, Y] the set of edges of G with one end in X and the other end in Y. The neighborhood of a node v is denotedN(v).

Connectivity: The connectivity of a graph G=

(V, E) is the minimum size of a set S⊂V such that G\S is not connected. A graph isk-connected if its connectivity is at leastk.

2.2 st-numbering of a Graph Given a pair of nodes {s, t} in a 2-connected graph G, an st- numbering for G is a numbering for the nodes inG defined as follows [11]: the nodes ofGare numbered from 1 to n so that sreceives number 1, node t re- ceives number n, and every node except s and t is adjacent both to a lower-numbered and to a higher- numbered node. It is shown in [7] that such a numbering can be found in O(|V|+|E|).

2.3 Series-Parallel Graphs A GraphGisseries- parallel, with terminalssandt, if it can be produced by a sequence of the following operations:

1. Create a new graph, consisting of a single edge

(3)

betweensandt.

2. Given two series parallel graphs,X andY with terminalssX, tX and sY, tY respectively, form a new graphG=P(X, Y) by identifyings=sX=sY

and t=tX=tY. This is known as the parallel composition ofX andY.

3. Given two series parallel graphsX andY, with terminalssX, tX and sY, tY respectively, form a new graphG=S(X, Y) by identifyings=sX, tX= sY and t=tY. This is known as the series composition ofX andY.

It is easy to see that a series-parallel graph is 2- connected if, and only if, the last operation is a parallel composition.

2.4 Nonseparating Induced Cycles and Ear Decomposition LetH be a subgraph of a graphG.

Anear ofHinGis a nontrivial path inGwhose ends lie in H but whose internal vertices do not. An ear decomposition ofGis a decompositionG=P0∪· · ·∪Pk

of the edges ofGsuch thatP0is a cycle andPifori≥1 is an ear ofP0∪P1∪· · ·∪P_i−1 in G. It is known that every 2-connected graph has an ear decomposition (and vice-versa), and such a decomposition can be found in linear time.

A cycleC is anonseparating induced cycle of G ifG\C is connected and C has no chords. We say a cycleC avoids a nodeu, ifu /∈C.

Theorem 2.1. (Tutte [18]) Given a 3-connected graphG(V, E)let{t, r}be any edge ofGand letube any node ofG,r6=u6=t. Then there is a nonseparating induced cycle ofG through{t, r} and avoidingu.

Notice that since G is 3-connected in the previous theorem, every node in C has a neighbor in G\C.

Cheriyan and Maheshwari showed that the cycle in Theorem 2.1 can be found in O(E) [4]. Moreover, they showed that any 3-connected graph G has a nonseparating ear decomposition G=P0∪· · ·∪Pk

defined as follows: Let Vi=V(P0)∪V(P1)· · ·∪V(Pi), let Gi=G[Vi] and Gi=G[V\Vi]. We say that G=

P₀∪P1∪· · ·∪Pkis an ear decomposition through edge {t, r} and avoiding vertexu if the cycleP₀ contains edge {t, r}, and the last ear of length greater than one, say P_m, has u as its only internal vertex. An ear decompositionP₀∪P₁· · ·∪P_k of graphGthrough edge {t, r} and avoiding vertexu is a nonseparating ear decomposition if for all i, 0≤i<m, graph Gi is connected and each internal vertex of ear Pi has a neighbor inGi.

Theorem 2.2. (Cheriyan and Maheshwari [4]) Given an edge{t, r}and a vertex uof a 3-connected

graph G, a nonseparating induced cycle ofGthrough {t, r} and avoiding u, and a nonseparating ear decomposition can be found in time O(|V|+|E|).

2.5 Partitioning of Graphs to Connected Subgraphs The following theorem is the main ex- isting result in partitioning of graphs into connected subgraphs and is proved independently by Lov´az and Gyori [9, 13] by different methods.

Theorem 2.3. (Lov´az and Gyori [9, 13]) Let G=(V, E) be a k-connected graph. Let n=|V|, v1, v2, . . . , vk∈V and let n1, n2, . . . , nk be positive integers satisfyingn1+n2+· · ·+nk=n. Then, there exists a partition of V into (V1, V2. . . , Vk) satisfying vi∈Vi,|Vi|=ni, and G[Vi] is connected for i=1,2, . . . , k.

Although the existence of such a partition has long been proved, there is no polynomial-time algorithm to find such a partition for k>3. For k=2, it is easy to find such partition using st-numbering. For k=3, Wada and Kawaguchi [19] provided an O(n²) algorithm using the nonseparating ear decomposition of 3-connected graph.

2.6 Convex Embedding of Graphs In this subsection, we provide a short overview of the beauti- ful work by Linial, Lov´az, and Wigderson [12] on convex embedding of the k-connected graphs. Let Q={q1, q2, . . . , qm} be a finite set of points in R^d. The convex hull conv(Q) ofQis the set of all points Pm

i=1λiqi withP

i=1λi=1. The rank ofQis defined by rank(Q)=1+dim(conv(Q)). Q is in general position if rank(S)=d+1 for every (d+1)-subsetS⊆Q.

LetGbe a graph andX⊂V. A convexX-embedding ofGis any mappingf:V→R^|X|−1such that for each v∈V\X, f(v)∈conv(f(N(v))). We say that the convex embedding is in general position if the set f(V) of the points is in general position.

Theorem 2.4. (Linial, Lov´az, and Wigderson [12]) Let G be a graph on n vertices and 1<k<n. Then the following two conditions are equivalent:

1. Gisk-connected

2. For everyX⊂V with|X|=k,Ghas a convexX- embedding in general position.

Notice that the special case of the Theorem for k=2 asserts the existence of an st-numbering of a 2-connected graph. The proof of this theorem is inspired by physics. The embedding is found by letting the edges of the graph behave like ideal springs and letting its vertices settle. A formal summary

(4)

of the proof (1→2) is as follows (for more details see [12]). For each vi∈X, define f(vi) arbitrary in R^k−1 such that f(X) is in general position. Assign to every edge (u, v)∈Ea positive elasticity coefficient c_uv and letc∈R^|E|be the vector of coefficients. It is proved in [12] that for almost any coefficient vectorc, an embeddingfthat minimizes the potential function P=P

{u,v}∈Ecuvkf(u)−f(v)k²provides a convexX- embedding in general position (k.k is the Euclidean norm). Moreover, the embedding that minimizes P satisfies the set of equations,

f(v)= 1 cv

X

u∈N(v)

c_uvf(u) for all v∈V\X,

where c_v=P

u∈N(v)c_uv. Hence, the embedding can be found by solving a set of linear equations, in at mostO(|V|³) time (or matrix multiplication time).

3 Balancing the Supply/Demand Only In this section, we study the single objective problem of finding a partition of the graph into connected subgraphs that balances (approximately) the supply and demand in each part of the partition, without any regard to the sizes of the parts. We can state the optimization problem as follows, and will refer to it as the Balanced Connected Partition with Integer weights (BCPI) problem.

Definition 3.1. Given a graph G=(V, E) with a weight (supply/demand) functionp: V → Zsatisfy- ingP

j∈V p(j)=0. The BCPI problem is the problem of partitioning V into(V₁, V₂)such that

1. V1∩V2=∅ andV1∪V2=V, 2. G[V1] andG[V2] are connected,

3. |p(V1)|+|p(V2)| is minimized, where p(V_i)=

P

j∈V_ip(j).

Clearly, the minimum possible value for|p(V1)|+

|p(V2)| that we can hope for is 0, which occurs iff p(V1)=p(V2)=0. It is easy to show that the problem of determining whether there exists such a ‘perfect’

partition (and hence the BCPI problem) is strongly NP-hard. The proof is very similar to analogous results concerning the partition of a graph into two connected subgraphs with equal sizes (or weights, when nodes have positive weights) [3, 6].

Proposition 3.1. (1) It is strongly NP-hard to determine whether there is a solution to the BCPI problem with value 0, even whenG is 2-connected.

(2) IfGis not 2-connected, then this problem is NP- hard even when∀i, p(i)=±1.

Although it is NP-hard to tell whether there is a solution satisfying p(V1)=p(V2)=0, even when

∀i, p(i)=±1, in this case, if the graphGis 2-connected there is always such a solution. For general weights p, there is a solution such that |p(V₁)|,|p(V₂)|≤

max_j∈V |p(j)|/2 and it can be found easily in linear time using thest-numbering between two nodes. (See the full paper for the proofs.)

Proposition 3.2. LetGbe a 2-connected graph and u, v any two nodes inV such that p(u)p(v)>0.

(1) There is a solution such that u∈V1, v∈V2, and

|p(V1)|=|p(V2)|≤maxj∈V |p(j)|/2.

(2) If ∀i, p(i)=±1, we can find a solution such that u∈V₁,v∈V₂, andp(V₁)=p(V₂)=0.

In both cases, the solution can be found in O(|E|) time.

Remark. The bound in Proposition 3.2 (1) is tight. A simple example is a cycle of length 4 like (v₁, v₂, v₃, v₄) withp(v₁)=−p,p(v₂)=−p/2,p(v₃)=p, andp(v₄)=p/2. It is easy to see that in this example

|p(V₁)|+|p(V₂)|=max_j∈V |p(j)|=pis the best that one can do.

3.1 Connected Partitioning into Many Parts The BCPI problem can be extended to partitioning a graph into k=3 or more parts. Let G=(V, E) be a graph with a weight function p : V → Z satisfying P

j∈V p(j)=0. The BCPIk problem is the problem of partitioning G into (V1, V2, . . . , Vk) such that for any 1≤i≤k, G[Vi] is connected and Pk

i=1|p(Vi)| is minimized.

In the following proposition, we show that for k=3, if p(i)=±1,∀i, then there is always a perfect partition (i.e., with p(V₁)=p(V₂)=p(V₃)=0) and it can be found efficiently. For general p, we can find a partition such that |p(V1)|+|p(V2)|+|p(V3)|≤

2 max_j∈V |p(j)|. The proof and the algorithm use a similar approach as the algorithm in [19] for partitioning a 3-connected graph to three connected parts with prescribed sizes, using the nonseparating ear decomposition of 3-connected graphs as described in Sub- section 2.4. (See the full paper for the proof.) Proposition 3.3. LetGbe a 3-connected graph and u, v, w three nodes in V such thatp(u), p(v), p(w)>0 or p(u), p(v), p(w)<0.

(1) There is a solution such thatu∈V1,v∈V2,w∈V3, and|p(V1)|+|p(V2)|+|p(V3)|≤2 max_j∈V |p(j)|.

(2) If ∀i, p(i)=±1, then there is a solution such that u∈V1,v∈V2,w∈V3, and|p(V1)|=|p(V2)|=|p(V3)|=0.

In both cases, the solution can be found in O(|E|) time.

(5)

4 Balancing Both Objectives

In this section, we formally define and study the Dou- bly Balanced Connected graph Partitioning (DBCP) problem.

Definition 4.1. Given a graph G=(V, E) with a weight (supply/demand) function p : V → Z satis- fyingp(V)=P

j∈V p(j)=0and constantscp≥0,cs≥1.

The DBCP problemis the problem of partitioningV into(V1, V2)such that

1. V1∩V2=∅ andV1∪V2=V, 2. G[V₁] andG[V₂] are connected, 3. |p(V₁)|,|p(V₂)|≤c_p and max{^|V_|V¹^|

2|,^|V_|V²^|

1|}≤c_s, wherep(Vi)=P

j∈Vip(j).

Remark. Our techniques apply also to the case that p(V)6=0. In this case, the requirement 3 onp(V1) and p(V2) is|p(V1)−p(V)/2|,|p(V2)−p(V)/2|≤cp, i.e., the excess supply/demand is split approximately evenly between the two parts.

We will concentrate on 2-connected and 3- connected graphs and show that we can construct efficiently good partitions. For most of the section we will focus on the case thatp(i)=±1,∀i∈V. This case contains all the essential ideas. All the techniques generalize to the case of arbitrary p, and we will state the corresponding theorems.

We observed in Section 2 that if the graph is 2- connected andp(i)=±1,∀i∈V then there is always a connected partition that is perfect with respect to the weight objective,p(V1)=p(V2)=0, i.e., (3) is satisfied with cp=0. We know also from [9, 13] that there is always a connected partition that is perfect with respect to the size objective,|V1|=|V2|, i.e., condition 3 is satisfied withc_s=1. The following observations show that combining the two objectives makes the problem more challenging. If we insist onc_p=0, then c_s cannot be bounded in general, (it will be Ω(|V|)), and if we insist onc_s=1, thenc_p cannot be bounded.

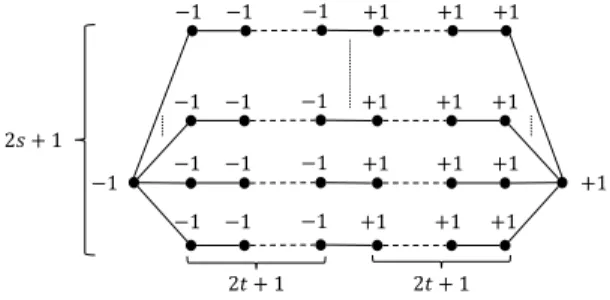
The series-parallel graphs of Figure 1 provide simple counterexamples.

Observation 1. If cp=0, then for anycs<|V|/2−1, there exist a 2-connected graphGsuch that the DBCP problem does not have a solution even when∀i, p(i)=

±1.

Proof. In the graph depicted in Figure 1, sett=0.

Observation 2. If cs=1, then for any cp<|V|/6, there exist a 2-connected graphGsuch that the DBCP problem does not have a solution even when∀i, p(i)=

±1.

−1

+1 +1 +1 +1 +1 +1 +1 +1 +1 +1

−1

2𝑡 + 1 2𝑡 + 1

−1 −1 −1 +1 +1 +1

2𝑠 + 1

Figure 1: Series-parallel graphs with 2s+1 paths of length 4t+2 used in Observations 1 and 2.

Proof. In the graph depicted in Figure 1, sets=1.

Thus, cp has to be at least 1 to have any hope for a bounded cs. We show in this section that cp=1 suffices for all 2-connected graphs. We first treat 3- connected graphs.

4.1 3-Connected Graphs LetG=(V, E) be a 3- connected graph. Assume for most of this section that ∀i, p(i)=±1 and p(V)=0 (we will state the results for general p at the end). We show that G has a partition that is essentially perfect with respect to both objectives, i.e., withcp=0 andcs=1.

We say “essentially”, because p(V1)=p(V2)=0 and

|V1|=|V2| imply that |V1|=|V2| are even, and hence V must be a multiple of 4. If this is the case, then indeed we can find such a perfect partition. If

|V|≡2(mod 4) (|V| has to be even since p(V)=0), then we can find an ‘almost perfect’ partition, one in which |p(V1)|=|p(V2)|=1 and |V1|=|V2| (also one in whichp(V₁)=p(V₂)=0 and|V1|=|V2|+2).

We first treat the case thatGcontains a triangle (i.e., cycle of length 3). In the following Lemma, we use the embedding fork-connected graphs introduced in [12] and as described in Subsection 2.6, to show that if G is 3-connected with a triangle and all weights are±1, then the DBCP problem has a perfect solution.

Lemma 4.1. If G is 3-connected with a triangle,

∀i, p(i)=±1, and |V|≡0(mod 4), then there exists a solution to the DBCP problem with p(V1)=p(V2)=0 and |V1|=|V2|. If |V|≡2(mod 4), then there is a solution with p(V₁)=p(V₂)=0 and |V1|=|V2|+2. More- over, this partition can be found in polynomial time.

Proof. Assume that|V|≡0(mod 4); the proof for the case|V|≡2(mod 4) is similar. In [12] as described in Subsection 2.6, it is proved that ifGis ak-connected graph, then for every X⊂V with |X|=k, G has a convex X-embedding in general position. Moreover, this embedding can be found by solving a set of linear equations of size |V|. Now, assumev, u, w∈V form a

(6)

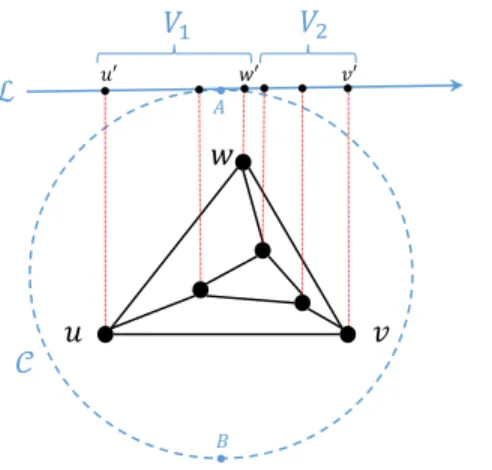
triangle inG. Set X={v, u, w}. Using the theorem, G has a convex X-embedding f:V→R² in general position. Consider a circle C around the triangle f(u), f(v), f(w) in R² as shown in an example in Fig. 2. Also consider a directed line L tangent to the circleC at pointA. If we project the nodes of G onto the line L, since the embedding is convex and also{u, v},{u, w},{w, v}∈E, the order of the nodes’

projection gives an st-numbering between the first and the last node (notice that the first and last nodes are always from the setX). For instance in Fig. 2, the order of projections give anst-numbering between the nodesuandvinG. Hence, if we setV1to be the|V|/2 nodes whose projections come first and V2 are the

|V|/2 nodes whose projections come last, thenG[V1] and G[V2] are both connected and |V1|=|V2|=|V|/2.

The only thing that may not match is p(V₁) and p(V₂). Notice that for each directed line tangent to the circleC, we can similarly get a partition such that

|V₁|=|V₂|=|V|/2. So all we need is a pointD on the circleCsuch that if we partition based on the directed line tangent to C at point D, then p(V₁)=p(V₂)=0.

To find such a point, we moveLfrom being tangent at point A to point B (AB is a diameter of the circleC) and consider the resulting partition. Notice that if at point A, p(V1)>0, then at point B since V1 andV2 completely switch places compared to the partition at pointA,p(V1)<0. Hence, as we moveL from being tangent at point A to point B and keep it tangent to the circle, in the resulting partitions, p(V1) goes from some positive value to a non-positive value. Notice that the partition (V₁, V₂) changes only if L passes a point D on the circle such that at D, L is perpendicular to a line that connects f(i) to f(j) for some i, j∈V. Now, since the embedding is in general position, there are exactly two points on every line that connects two pointsf(i) andf(j), so V1 changes at most by one node leavingV1 and one node enteringV1 at each step as we moveL. Hence, p(V1) changes by either±2 or 0 value at each change.

Now, since|V|≡0(mod 4),p(V1) has an even value in all the resulting partitions. Therefore, as we move L from being tangent at point A to pointB, there must be a pointDsuch that in the resulted partition p(V1)=p(V2)=0.

It is also easy to see that since V1 may change only when a line that passes through 2 nodes of graph G is perpendicular to L, we can find D in at most O(|V|²) steps.

When G is a triangle-free 3-connected graph, however, the proof in Lemma 4.1 cannot be directly used anymore. The reason is if for example{u, v}∈E/ and we project the nodes of Gonto the lineL, this time

𝑢 𝑣

𝑤

𝐴

𝐵

𝑢′ 𝑤′ 𝑣′

ℒ

𝒞

𝑉₁ 𝑉2

Figure 2: Proof of Lemma 4.1.

the order of the nodes projection does not give an st-numbering between the first and the last node if for exampleuandware the first and last node, since some of the middle nodes may only be connected tov.

To prove a similar result for triangle-free 3-connected case, we first provide the following two Lemmas. The main purpose of the following two Lemmas are to compensate for the triangle-freeness ofGin the proof of Lemma 4.1. The idea is to show that in every 3- connected graph, there is a triple {u, w, v}∈V, such that {u, w},{w, v}∈E and in every partition that we get by the approach used in the proof of Lemma 4.1, ifuandv are inV_i, so is a path betweenuandv.

Lemma 4.2. If Gis 3-connected, then there exists a set {u, v, w}⊂V and a partition of V into (V₁⁰, V₂⁰) such that:

1. V₁⁰∩V₂⁰=∅ andV₁⁰∪V₂⁰=V, 2. G[V₁⁰] andG[V₂⁰] are connected, 3. {u, w},{v, w}∈E,

4. w∈V₁⁰,u, v∈V₂⁰, 5. |V₂⁰|≤|V|/2.

Moreover, such a partition and{u, v, w}can be found in O(|E|)time.

Proof. Using the algorithm presented in [4], we can find a non-separating cycle C0 in Gsuch that every node in C0 has a neighbor in G\C0 in O(|E|) time.

Now, we consider two cases:

(i) If |C0|≤|V|/2+1, then select any three consec- utive nodes (u, w, v) of C0 and set V₂⁰=C0\{w}

andV₁⁰=V\V₂⁰.

(ii) If |C0|>|V|/2+1, since every node in C0 has a neighbor in G\C0, there exists a nodew∈V\C0

(7)

𝑢 𝑣 𝑤

𝑉₁′ 𝑉₂′

ℒ

₁

ℒ

₂

ℒ

₃

𝐵

ℒ

𝒞

𝐴

(0,0.5) (0.5,0.5)

(0,0) (0,1)

(1,0)

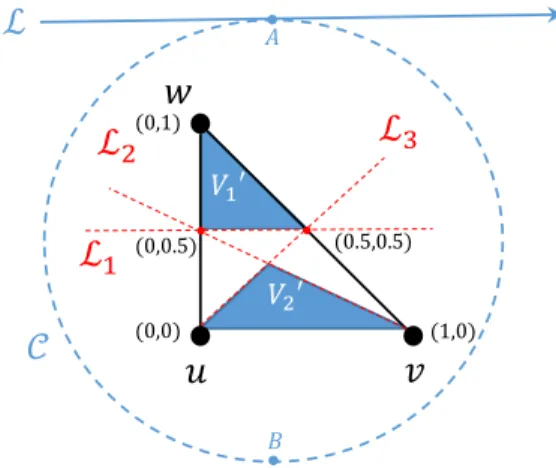
Figure 3: Proof of Lemma 4.3 and Theorem 4.1.

such that|N(w)∩C0|≥2. Select two nodes u, v∈

N(w)∩C0. There exists a path P in C0 from u to v such that |P|<|V|/2+1. Set V₂⁰=P and V₁⁰=V\V₂⁰.

Lemma 4.3. Given a partition (V₁⁰, V₂⁰) of a 3- connected graph G with properties described in Lemma 4.2, Ghas a convexX-embedding in general position with mappingf:V→R² such that:

1. X={u, w, v}, f(u)=(0,0), f(v)=(1,0), and f(w)=(0,1),

2. Every node i in V₁⁰ is mapped to a point (f1(i), f2(i))with f2(i)≥1/2,

3. Every node i in V₂⁰ is mapped to a point (f1(i), f2(i))withf1(i)≥f2(i)andf1(i)+2f2(i)≤

1.

Moreover, such an embedding can be found in polynomial time.

Sketch of the proof. Set X={v, u, w}. Using [12], G has a convexX-embedding inR²in general position with mappingf:V→R²such thatf(u)=(0,0),f(v)=

(1,0), and f(w)=(0,1). In the X-embedding of the nodes, we have a freedom to set the elasticity coefficient vector~cto anything that we want (except a measure zero set of vectors). So for any edge{i, j}∈

G[V₁⁰]∪G[V₂⁰], setcij=g; and for any{i, j}∈E[V₁⁰, V₂⁰], setcij=1. Since bothG[V₁⁰] andG[V₂⁰] are connected, as we increaseg, nodes inV₁⁰get closer towand nodes inV₂⁰ get closer to the lineuv (asg→∞, nodes inV₁⁰ get in the same position aswand node inV₂⁰ get on the line uv). Hence, intuitively there exists a value g (with polynomially many bits), for which all the nodes inV1 are above lineL1and all the nodes inV₂⁰

are below the lines L2 and L3 as depicted in Fig. 3.

See the full paper for the detailed proof which shows also that agwith polynomially many bits suffices.

Using Lemmas 4.2 and 4.3, we are now able to prove that for any 3-connected graph Gsuch that all the weights are±1, the DBCP problem has a solution forc_p=0 andc_s=1. The idea of the proof is similar to the proof of Lemma 4.1, however, we use Lemma 4.2 to find a desirable partition (V₁⁰, V₂⁰) and then use this partition to find an embedding with properties as described in Lemma 4.3. By using this embedding, we can show that in every partition that we obtain by the approach in the proof of Lemma 4.1, ifuandv are in Vi, so is a path betweenuandv. This implies then thatG[V1] and G[V2] are connected. So we can use similar arguments as in the proof of Lemma 4.1 to prove the following theorem.

Theorem 4.1. IfGis 3-connected,∀i, p(i)=±1, and

|V|≡0(mod 4), then there exists a solution to the DBCP problem withp(V₁)=p(V₂)=0and|V1|=|V2|. If

|V|≡2(mod 4), then there is a solution with p(V₁)=

p(V₂)=0 and |V₁|=|V₂|+2. Moreover, this partition can be found in polynomial time.

It is easy to check for a 3-connected graph G, by using the same approach as in the proof of Lemma 4.1 and Theorem 4.1, that even when the weights are arbitrary (not necessarily ±1) and also p(V)6=0, we can still find a connected partition (V1, V2) forGsuch that|p(V1)−p(V)/2|,|p(V1)−

p(V)/2|≤max_i∈V |p(i)|and|V1|=|V2|.

Corollary 4.1. If G is 3-connected, then the DBCP problem (with arbitrary p, and not necessarily satisfying p(V)=0) has a solution for cp= maxi∈V|p(i)| andcs=1. Moreover, this solution can be found in polynomial time.

4.2 2-Connected Graphs We first define a pseudo-path between two nodes in a graph as below.

The definition is inspired by the definition of the st- numbering.

Definition 4.2. A pseudo-path between nodes u and v in G=(V, E), is a sequence of nodesv₁, . . . , v_t such that ifv0=uandvt+1=v, then for any1≤i≤t,vi

has neighbors vj andvk such that j<i<k. Note that the pseudo-path does not include the ending pointsu andv.

Using the pseudo-path notion, in the following lemma we show that ifGis 2-connected and has a separation pair such that none of the resulting components are too large, then the DBCP problem always has a solution for some cp=cs=O(1). The idea used in the

(8)

𝑢

𝑣 𝑄1

𝑄₂ (a)

𝑢

𝑣 𝑉1

𝑉₂

𝑉′

(b)

𝑢

𝑣 𝑉₁

𝑉₂

𝑉′

(c)

𝑢

𝑣 𝑉₁

𝑉2 𝑉′

𝑉′′′

(d)

𝑢

𝑣 𝑉1

𝑉₂

𝑉′

𝑉′′′

(e) Figure 4: Proof of Lemma 4.4.

proof of this lemma is one of the building blocks of the proof for the general 2-connected graph case.

Lemma 4.4. Given a 2-connected graphGand an integerq≥3, if∀i:p(i)=±1andGhas a separation pair {u, v}⊂V such that for every connected component Hi=(VH_i, EH_i) of G[V\{u, v}], |VH_i|<(q−1)|V|/q, then the DBCP problem has a solution for cp=1, cs=q−1, and it can be found inO(|E|)time.

Proof. Assume for simplicity that |V| is divisible by q. There is a separation pair {u, v}∈V such that if H1, . . . , Hk are the connected components of G\{u, v}, for any i, |VH_i|<(q−1)|V|/q. Since G is 2-connected, H1, . . . , Hk can be presented by pseudo-paths P1, . . . , Pk between u and v. Assume P1, . . . , Pk are in increasing order based on their

lengths. There exists two subsets of the pseudo-paths S1 andS2 such that S1∩S2=∅,S1∪S2={P1, . . . , Pk} and P

P_j∈Si|Pj|≥|V|/q−1 for i=1,2. The proof is very simple. Add greedily pseudo-paths in order to S1 until its size becomes at least|V|/q−1. Let S1= {P1, . . . , Pi}, and S2={Pi+1, . . . , Pk}. Since |Pk|<

(q−1)|V|/q, we have i<k, and S26=∅. We have to show that |S2|≥|V|/q−1. If |Pk|≥|V|/q−1, then also|S2|≥|V|/q−1. If|Pk|<|V|/q−1, then|P1|+. . .+

|Pi−1|<|V|/q−1 and |Pi|≤|Pk|<|V|/q−1 imply that

|S₂|≥|V|/q−1, sinceq≥3.

Now, if we put all the pseudo-paths inS₁back to back, they will form a longer pseudo-pathQ₁between uandv. Similarly, we can form another pseudo-path Q2 from the pseudo-paths in S2 (Fig. 4a). Without loss of generality we can assume |Q1|≥|Q2|. Fromu,

(9)

includinguitself, we count|V|/qof the nodes inQ1

towards v and put them in a set V⁰. Without loss of generality, we can assume p(V⁰)≥0. If p(V⁰)=0, then (V⁰, V\V⁰) is a good partition and we are done.

Hence, assumep(V⁰)>0. We keepV⁰ fixed and make a new set V⁰⁰ by continuing to add nodes from Q₁ to V⁰ one by one before we get to v. Ifp(V⁰⁰) hits 0 as we add nodes one by one, we stop and letV1=V⁰⁰ andV2=V\V⁰⁰, then (V1, V2) is a good partition and we are done (Fig. 4b). So, assumeV⁰⁰=Q1∪{u}and p(V⁰⁰)>0. Since |Q2∪{v}|≥|V|/q, |V⁰⁰|≤(q−1)|V|/q.

If|V⁰⁰|<(q−1)|V|/q, we add nodes from Q2∪{v}one by one toward u until either p(V⁰⁰)=0 or |V⁰⁰|=(q−

1)|V|/q. If we hit 0 first (i.e., p(V⁰⁰)=0) and |V⁰⁰|≤

(q−1)|V|/q, defineV1=V⁰⁰\{u}, then (V1, V\V1) is a good partition (Fig. 4c). So assume|V⁰⁰|=(q−1)|V|/q and p(V⁰⁰)>0. Define V⁰⁰⁰=V\V⁰⁰. Since p(V⁰⁰)>0 and |V⁰⁰|=(q−1)|V|/q, then p(V⁰⁰⁰)<0 and |V⁰⁰⁰|=

|V|/q. Also notice that V⁰⁰⁰⊆Q2. We consider two cases. Either|p(V⁰)|≥|p(V⁰⁰⁰)|or|p(V⁰)|<|p(V⁰⁰⁰)|.

If |p(V⁰)|≥|p(V⁰⁰⁰)|, then if we start from uand pick nodes one by one fromQ₁ in order, we can get a subsetV₁⁰ ofV⁰ such that|p(V₁⁰)|=|p(V⁰⁰⁰)|. Hence, if we define V1=V₁⁰∪V⁰⁰⁰, then (V1, V\V1) is a good partition (Fig. 4d).

If |p(V⁰)|<|p(V⁰⁰⁰)|, then we can build a new set V1 by adding nodes one by one from Q2 to V⁰ until P(V1)=0. It is easy to see that since |p(V⁰)|<

|p(V⁰⁰⁰)|, then V1\V⁰⊆V⁰⁰⁰. Hence, (V1, V\V1) is a good partition (Fig. 4e).

Corollary 4.2. If G is a 2-connected series- parallel graph and∀i:p(i)=±1, then the DBCP problem has a solution forc_p=1, c_s=2, and the solution can be found in O(|E|)time.

The graph in Figure 1 with s=1 shows that these parameters are the best possible for series parallel graphs: ifcp=O(1) thencs must be at least 2.

To generalize Lemma 4.4 to all 2-connected graphs, we need to define the contractible subgraph and thecontraction of a given graph as below.

Definition 4.3. We say an induced subgraph H of a 2-connected graph G is contractible, if there is a separating pair {u, v}⊂V such that H=(VH, EH) is a connected component of G[V\{u, v}]. Moreover, if we replace H by a weighted edge e⁰ with weight w(e⁰)=|VH|between the nodesuandv inGto obtain a smaller graph G⁰, we say Gis contractedtoG⁰. Remark. Notice that every contractible subgraph of a 2-connected graphG can also be represented by a pseudo-path between its associated separating pair.

We use this property in the proof of Theorem 4.2.

Using the notion of the graph contraction, in the following lemma, we show that to partition a 2- connected graph, we can reduce it to one of two cases:

either Gcan be considered as a graph with a set of short pseudo-paths between two nodes, or it can be contracted into a 3-connected graph as illustrated in Fig. 5.

Lemma 4.5. In every 2-connected graph G=(V, E), given an integerq≥3, one of the following cases holds, and we can determine which in O(|E|) time:

1. There is a separation pair {u, v}⊂V such that if H1, . . . , Hk are the connected components of G[V\{u, v}], for alli,|VHi|<(q−1)|V|/q.

2. After a set of contractions, G can be trans- formed into a 3-connected graph G^∗=(V^∗, E^∗) with weighted edges representing contracted subgraphs such that for every e^∗∈E^∗,w(e^∗)<|V|/q.

Proof. If there is no separation pairs in G, then G is 3-connected and there is nothing left to prove. So assume{u, v}⊂V is a separation pair andH1, . . . , Hk

are the connected components of G[V\{u, v}]. If

∀i,|VH_i|<(q−1)|V|/q, we are done. So let’s assume there is a connected component Hj such that|VH_j|≥

(q−1)|V|/q. Then for every i6=j, Hi can be contracted and represented by an edge of weight less than |V|/q between u and v. Now, we repeat the process by considering the weight of the edges in the size of each connected component (a weighted edge can be contracted again as part of a new connected component and its weight will be added to the total number of nodes in that connected component). An example for each case is shown in Fig. 5 forq=3. We can find either a suitable separation pair as in case 1 or a suitable contracted graph G^∗ as in case 2 in linear time using the Hopcroft-Tarjan algorithm for finding the triconnected components [10].

Using Lemma 4.5 for q=4, then Lemma 4.4, and the idea of the proof for Theorem 4.1, we can prove that when G is 2-connected and all p(i)=±1, the DBCP problem has a solution for c_p=1 and c_s=3. There are some subtleties in adapting Lemma 4.2 for this case to account for the fact that the edges ofG^∗ are now weighted, and the partition (V₁⁰, V₂⁰) has to take into account the edge weights. We find a suitable convex embedding of the 3-connected graph G^∗ and then embed the nodes of the contracted pseudo-paths appropriately along the segments corresponding to the weighted edges. Some care is needed to carry out the argument of the 3-connected case, since as the line tangent to the circle rotates, the order of the projections of many nodes may change at once,

(10)

𝑣₁

𝑣₂

𝑣₃ 𝑣₅

𝑣₄

𝑣₇ 𝑣₆

𝐺

𝑣₃

𝑣7

𝐻₁ 𝐻₂ 𝐻₃

1 3 1

(a)

𝑣₁₁ 𝑣₁

𝑣₂ 𝑣₃ 𝑣₄ 𝑣₇

𝑣₉ 𝑣₈

𝑣₁₀

𝐺 𝐺 ^∗

𝑣₅ 𝑣₆

𝑣₁₂ 𝑣₁₃

𝑣₁₄ 𝑣₁₅

𝑣11

𝑣₁

𝑣₂ 𝑣₃ 𝑣₄ 𝑣₇

𝑣₅ 𝑣₆

𝑣₁₂ 𝑣₁₃

𝑣14 𝑣₁₅ 3

3

𝑣₁₁ 𝑣₁

𝑣₇

𝑣₆ 𝑣₁₂ 𝑣₁₃

𝑣₁₄ 𝑣₁₅ 3 𝑣₅

(b)

Figure 5: Lemma 4.5.

namely the nodes on an edge perpendicular to the rotating line. The details of the proof are given in the full paper. We have:

Theorem 4.2. If G is 2-connected, ∀i, p(i)=±1, then the DBCP problem has a solution forc_p=1 and c_s=3. Moreover, this solution can be found in polynomial time.

Similar to Corollary 4.1, the approach used in the proof of Theorem 4.2, can also be used for the case when the weights are arbitrary (not necessarily ±1) andp(V)6=0. It can be shown that in this case, ifG is 2-connected, the DBCP problem has a connected partition (V1, V2) such that |p(V1)−p(V)/2|,|p(V2)−

p(V)/2|≤max_j∈V |p(j)| and|V1|,|V2|≥|V|/4.

Corollary 4.3. If G is 2-connected, then the DBCP problem (with general p and not necessarily satisfying p(V)=0) has a solution for cp= max_j∈V |p(j)|andcs=3. Moreover, this solution can be found in polynomial time.

5 Graphs with Two Types of Nodes

Assume Gis a connected graph with nodes colored either red (R⊆V) or blue (B⊆V). Let |V|=n, |R|=

nr, and |B|=nb. If G is 3-connected, set p(i)=1 if i∈R andp(i)=−1 if i∈B. Corollary 4.1 implies then that there is always a connected partition (V1, V2) of V that splits both the blue and the red nodes evenly

(assuming n_r and n_b are both even), i.e., such that

|V1|=|V2|, |R∩V1|=|R∩V2|, and |B∩V1|=|B∩V2|. (If n_r and/orn_b are not even, then one side will contain one more red or blue node.)

Corollary 5.1. Given a 3-connected graph Gwith nodes colored either red (R⊆V) or blue (B⊆V).

There is always a partition (V1, V2) of V such that G[V1] and G[V2] are connected, |V1|=|V2|, |R∩V1|=

|R∩V2|, and|B∩V1|=|B∩V2| (assuming |R| and |B|

are both even). Such a partition can be computed in polynomial time.

Proof. Suppose without loss of generality thatnr≥nb

and letnr−nb=2tandnr+nb=n=2m. Setp(i)=1 for i∈Randp(i)=−1 fori∈B. Thenp(V)=2t. From the equations, we havenr=m+tandnb=m−t.

From Corollary 4.1 we can find a partition (V1, V2) such that |V1|=|V2| and |p(V1)−

p(V)/2|,|p(V1)−p(V)/2|≤1. Letr1=|R∩V1|andb1=

|B∩V1|. We have r1+b1=n/2=m and t−1≤r1− b₁≤t+1. Therefore, (m+t)/2−(1/2)≤r1≤(m+t)/2+

(1/2). Since r₁ is an integer and n_r=m+t is even, it follows that r₁=(m+t)/2=n_r/2. Hence, b₁=(m−

t)/2=n_b/2. Therefore, V₂ also contains n_r/2 red nodes and n_b/2 blue nodes.

If Gis only 2-connected, we may not always get a perfect partition. Assume wlog that nr≤nb. If for every v∈R and u∈B, we set p(v)=1 and p(u)=

(11)

−nr/nb, Corollary 4.3 implies that there is always a connected partition (V1, V2) of V such that both

|(|R∩V1|−nr/n_b|B∩V1|)|≤1 and|(|R∩V2|−nr/n_b|B∩ V2|)|≤1, and also max{^|V_|V¹^|

2|,^|V_|V²^|

1|}≤3. Thus, the ratio of red to blue nodes in each side V_i differs from the ration_r/n_b in the whole graph byO(1/n). Hence if the numbers of red and blue nodes areω(1), then the two types are presented in both sides of the partition in approximately the same proportion as in the whole graph.

Corollary 5.2. Given a 2-connected graph Gwith nodes colored either red (R⊆V) or blue (B⊆V), and assume wlog |R|≤|B|. We can always find in polynomial time a partition (V1, V2) of V such that G[V1] andG[V2] are connected, |V1|,|V2|≥|V|/4, and the ratio of red to blue nodes in each side Vi differs from the ratio|R|/|B|in the whole graph by O(1/n).

6 Conclusion

In this paper, we introduced and studied the problem of partitioning a graph into two connected subgraphs that satisfy simultaneouly two objectives: (1) they balance the supply and demand within each side of the partition (or more generally, for the case of p(V)6=0, they split approximately equally the excess supply/demand between the two sides), and (2) the two sides are large and have roughly compara- ble size (they are both Ω(|V|)). We showed that for 2-connected graphs it is always possible to achieve both objectives at the same time, and for 3-connected graphs there is a partition that is essentially perfectly balanced in both objectives. Furthermore, these partitions can be computed in polynomial time. This is a paradigmatic bi-objective balancing problem. We observed how it can be easily used to find a connected partition of a graph with two types of nodes that is balanced with respect to the sizes of both types.

Overall, we believe that the novel techniques used in this paper can be applied to partitioning heteroge- neous networks in various contexts.

There are several interesting further directions that suggest themselves. First, extend the theory and algorithms to find doubly balanced connected partitions to more than two parts. Second, even considering only the supply/demand objective, does the analogue of the results of Lov´az and Gyori [9, 13]

for the connected k-way partitioning of k-connected graphs with respect to size (which corresponds to p(i)=1) extend to the supply/demand case (p(i)=±1) for k>3? And is there a polynomial algorithm that constructs such a partition? Finally, extend the results of Section 5 to graphs with more than two types of nodes, that is, can we partition (under suitable con-

ditions) a graph with several types of nodes to two (or more) large connected subgraphs that preserve approximately the diversity (the proportions of the types) of the whole population?

References

[1] D. Bienstock. Electrical Transmission System Cas- cades and Vulnerability: An Operations Research Viewpoint, volume 22. SIAM, 2016.

[2] J. Bondy and U. Murty. Graph theory, 2nd printing, 2008.

[3] F. Chataigner, L. R. Salgado, and Y. Wakabayashi.

Approximation and inapproximability results on balanced connected partitions of graphs. DMTCS, 9(1):177–192, 2007.

[4] J. Cheriyan and S. Maheshwari. Finding nonseparating induced cycles and independent spanning trees in 3-connected graphs. J. Algorithms, 9(4):507–537, 1988.

[5] J. Chleb´ıkov´a. Approximating the maximally balanced connected partition problem in graphs. In- form. Process. Lett., 60(5):225–230, 1996.

[6] M. Dyer and A. Frieze. On the complexity of partitioning graphs into connected subgraphs. Discrete Applied Math., 10:139–153, 1985.

[7] S. Even and R. E. Tarjan. Computing an st-numbering. Theoretical Computer Science, 2(3):339–344, 1976.

[8] N. Fan, D. Izraelevitz, F. Pan, P. M. Pardalos, and J. Wang. A mixed integer programming approach for optimal power grid intentional islanding.Energy Systems, 3(1):77–93, 2012.

[9] E. Gyori. On division of graphs to connected subgraphs. In Combinatorics (Proc. Fifth Hungarian Colloq., Keszthely, 1976), volume 1, pages 485–494, 1976.

[10] J. E. Hopcroft and R. E. Tarjan. Dividing a graph into triconnected components. SIAM J. Comput., 2(3):135–158, 1973.

[11] A. Lempel, S. Even, and I. Cederbaum. An algorithm for planarity testing of graphs. InTheory of graphs: International symposium, volume 67, pages 215–232. Gordon and Breach, New York, 1967.

[12] N. Linial, L. Lovasz, and A. Wigderson. Rubber bands, convex embeddings and graph connectivity.

Combinatorica, 8(1):91–102, 1988.

[13] L. Lov´asz. A homology theory for spanning tress of a graph.Acta Mathematica Hungarica, 30(3-4):241–

251, 1977.

[14] S. Pahwa, M. Youssef, P. Schumm, C. Scoglio, and N. Schulz. Optimal intentional islanding to enhance the robustness of power grid networks. Physica A, 392(17):3741–3754, 2013.

[15] R. J. S´anchez-Garc´ıa, M. Fennelly, S. Norris, N. Wright, G. Niblo, J. Brodzki, and J. W.

Bialek. Hierarchical spectral clustering of power

(12)

grids. IEEE Trans. Power Syst., 29(5):2229–2237, 2014.

[16] K. Sun, Q. Zhao, D.-Z. Zheng, J. Ma, and Q. Lu. A two-phase method based on obdd for searching for splitting strategies of large-scale power systems. In Proc. IEEE PowerCon’02, 2002.

[17] H. Suzuki, N. Takahashi, and T. Nishizeki. A linear algorithm for bipartition of biconnected graphs.

Inform. Process. Lett., 33(5):227–231, 1990.

[18] W. T. Tutte. How to draw a graph. Proc. London Math. Soc, 13(3):743–768, 1963.

[19] K. Wada and K. Kawaguchi. Efficient algorithms for tripartitioning triconnected graphs and 3-edge- connected graphs. In Graph-Theoretic Concepts in Computer Science, pages 132–143. Springer, 1994.

[20] D. B. West et al. Introduction to graph theory, volume 2. Prentice hall Upper Saddle River, 2001.

Doubly Balanced Connected Graph Partitioning ∗