Face Recognition Using LDA Based Algorithms
Volltext
Abbildung
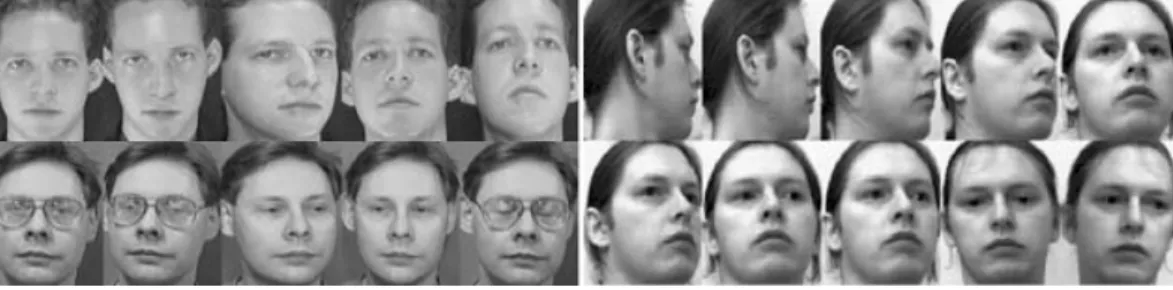
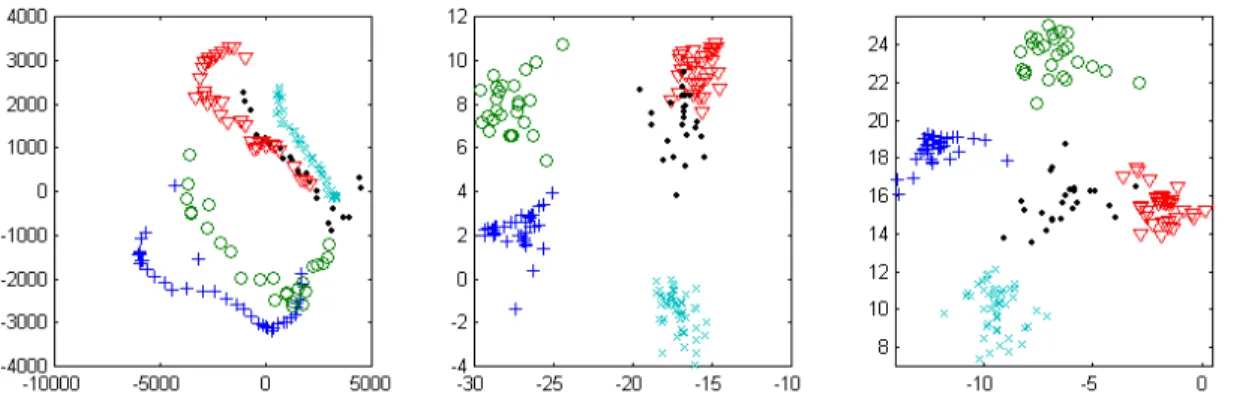


ÄHNLICHE DOKUMENTE
lerquote durch die Befund- übermittlung und Ergebnis- eintragung durchaus unter- stellt werden, viel wichtiger doch erscheint mir auch hier die eigentlich
The remainder of the paper is organized as follows: Sec- tion “Sentiment analysis and prediction algorithm based on the hybrid LDA-ARMA model” improved the LDA topic model and
With regard to children, some detainees argued that ‘… it is better for children to be here in prison than live outside on the streets,’ while others said ‘… living out- side
This table shows results of the WSJ data when us- ing all words of the documents for training a topic model and assigning topic IDs to new documents and also filtered results,
Tutorial Wannier Functions..
The face recognition approaches using thermal (long wave infrared, LWIR) images or the fusion of thermal and visible images can improve the recognition performance.. There is
Revocation and renewability management is possible with template protection: if a tem- plate is compromised, the same biometric characteristic can be used again to construct a
a certain graph, is shown, and he wants to understand what it means — this corre- sponds to reception, though it involves the understanding of a non-linguistic sign;