Berechenbarkeitstheorie: Teil II Prof. Dr. David Sabel

Formale Sprachen und Komplexit¨at

Sommersemester 2019

Berechenbarkeitstheorie: Teil II

Prof. Dr. David Sabel

LFE Theoretische Informatik

Inhalt

Ackermannfunktion

Primitiv rekursive Funktionen µ-rekursive Funktionen

Die Ackermannfunktion

Von Wilhelm Ackermann in 1920er Jahre vorgeschlagen sehr schnell wachsende Funktion

Variante von R´ozsa P´eter:

Ackermann-Funktiona: (N×N)→N

a(x, y) =







y+ 1, falls x= 0

a(x−1,1) falls x6= 0 undy = 0 a(x−1, a(x, y−1)) falls x >0 undy >0

Unser n¨achstes Ziel:

Die Ackermannfunktion ist WHILE-berechenbar, aber: die Ackermannfunktion istnicht LOOP-berechenbar (obwohl sie total ist)

Die Ackermannfunktion

Von Wilhelm Ackermann in 1920er Jahre vorgeschlagen sehr schnell wachsende Funktion

Variante von R´ozsa P´eter:

Ackermann-Funktiona: (N×N)→N

a(x, y) =







y+ 1, falls x= 0

a(x−1,1) falls x6= 0 undy = 0 a(x−1, a(x, y−1)) falls x >0 undy >0 Unser n¨achstes Ziel:

Die Ackermannfunktion ist WHILE-berechenbar, aber:

die Ackermannfunktion istnicht LOOP-berechenbar (obwohl sie total ist)

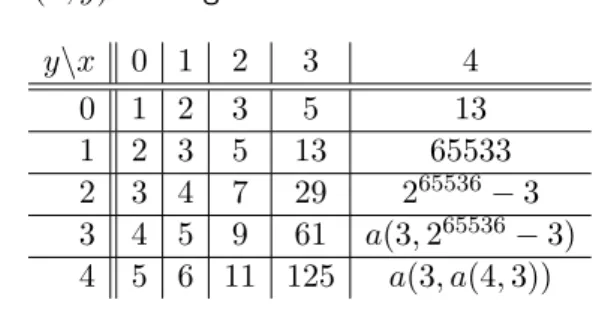
Einige Werte der Ackermannfunktion

Tabelle mita(x, y)-Eintr¨agen:

y\x 0 1 2 3 4

0 1 2 3 5 13

1 2 3 5 13 65533

2 3 4 7 29 2⁶⁵⁵³⁶−3

3 4 5 9 61 a(3,2⁶⁵⁵³⁶−3) 4 5 6 11 125 a(3, a(4,3))

Terminierung

a(x, y) =







y+ 1, falls x= 0

a(x−1,1) falls x6= 0 undy = 0 a(x−1, a(x, y−1)) falls x >0 undy >0 Mehrmaliges Entfalten der dritten Zeile zeigt:

a(x, y) = (a(x−1, a(x−1, a(x−1, . . . , a(x−1,

| {z }

y+1−mal

1). . .))))

Daher sind alle rekursiven Aufrufe echt kleiner und daher terminiert die Ackermannfunktion stets.

Lemma

Die Ackermannfunktion ist total.

Berechenbarkeit der Ackermannfunktion

Intuitiv klar: Mit jeder modernen Programmiersprache ist die Ackermannfunktion implementierbar. Daher ist sie auch (intuitiv) berechenbar.

Satz

Die Ackermannfunktion ist WHILE-berechenbar.

Beweis: Erstelle ein WHILE-Programm, welches die rekursive Berechnung durchf¨uhrt mit einem Stack.

Daher ist der erste Schritt im Beweis: Darstellung des Stacks

Implementierung von Operationen auf dem Stack als WHILE-Programm.

Danach wird das Programm angegeben, dass die Stackoperationen durchf¨uhrt.

Berechenbarkeit der Ackermannfunktion

Intuitiv klar: Mit jeder modernen Programmiersprache ist die Ackermannfunktion implementierbar. Daher ist sie auch (intuitiv) berechenbar.

Satz

Die Ackermannfunktion ist WHILE-berechenbar.

Beweis: Erstelle ein WHILE-Programm, welches die rekursive Berechnung durchf¨uhrt mit einem Stack.

Daher ist der erste Schritt im Beweis: Darstellung des Stacks

Implementierung von Operationen auf dem Stack als WHILE-Programm.

Danach wird das Programm angegeben, dass die Stackoperationen durchf¨uhrt.

Berechenbarkeit der Ackermannfunktion

Intuitiv klar: Mit jeder modernen Programmiersprache ist die Ackermannfunktion implementierbar. Daher ist sie auch (intuitiv) berechenbar.

Satz

Die Ackermannfunktion ist WHILE-berechenbar.

Beweis: Erstelle ein WHILE-Programm, welches die rekursive Berechnung durchf¨uhrt mit einem Stack.

Daher ist der erste Schritt im Beweis:

Darstellung des Stacks

Implementierung von Operationen auf dem Stack als WHILE-Programm.

Danach wird das Programm angegeben, dass die Stackoperationen durchf¨uhrt.

Vorbemerkung

Darstellung von Tupelfolgen mit fester L¨ange kals eine einzige Zahl:

hn₁, . . . , n_k,0i=c(n1, c(n2,(. . . , c(n_k,0). . .) wobei c(x, y) eine Bijektion (N×N)→Nist Wir nehmen an, dass left und right existieren mit left(c(x, y)) =xund right(c(x, y)) =y

Genauere Details zuc,left,right werden sp¨ater nochmal er¨ortert

Ackermannfunktion mit WHILE berechnen

Stack:

Stack: Folge von Zahlenn₁, . . . , n_k,0 sodassn₁ ganz oben liegt. Leerer Stack: 0 markiert Kellerboden.

Stack im WHILE-Programm: Variable stack, die Zahl hn₁, . . . , nk,0i=c(n1, c(n2,(. . . , c(nk,0). . .) speichert, und stacksize, die Gr¨oße des Stacks speichert

Stack-Operationen:

push(x, stack) legt Zahlx oben auf den Stack. WHILE-Programm dazu:

stack:=c(x, stack);stacksize:=stacksize+ 1.

x:=pop(stack) entfernt das oberste Element vom Stack und setzt x auf dessen Wert.

WHILE-Programm: x:=left(stack);stack=right(stack); stacksize:=stacksize−1

stacksize6= 1: WHILE-Programm dazu existiert

Ackermannfunktion mit WHILE berechnen

Stack:

Stack: Folge von Zahlenn₁, . . . , n_k,0 sodassn₁ ganz oben liegt. Leerer Stack: 0 markiert Kellerboden.

Stack im WHILE-Programm: Variable stack, die Zahl hn₁, . . . , nk,0i=c(n1, c(n2,(. . . , c(nk,0). . .) speichert, und stacksize, die Gr¨oße des Stacks speichert

Stack-Operationen:

push(x, stack) legt Zahlx oben auf den Stack.

WHILE-Programm dazu:

stack:=c(x, stack);stacksize:=stacksize+ 1.

x:=pop(stack) entfernt das oberste Element vom Stack und setzt x auf dessen Wert.

WHILE-Programm: x:=left(stack);stack=right(stack);

stacksize:=stacksize−1

stacksize6= 1: WHILE-Programm dazu existiert

WHILE-Programm zur Berechnung von a(x, y)

stack:= 0;

stacksize:= 0;

push(x, stack);

push(y, stack);

WHILEsize(stack)6= 1 DO y:=pop(stack);

x:=pop(stack);

IF x= 0

THEN push(y+ 1, stack);

ELSE IF y= 0 THEN push(x−1, stack);push(1, stack)

ELSEpush(x−1, stack);push(x, stack),push(y−1, stack);

END END END

result:=pop(stack);

Eigenschaften der Ackermannfunktion

Lemma

Die folgenden Monotonie-Eigenschaften gelten f¨ur die Ackermannfunktiona:

1 y < a(x, y)

2 a(x, y)< a(x, y+ 1)

3 a(x, y+ 1)≤a(x+ 1, y)

4 a(x, y)< a(x+ 1, y)

5 Falls x≤x⁰ und y≤y⁰, dann gilt aucha(x, y)≤a(x⁰, y⁰) Beweise im Skript (Induktion ¨uberx bzw. y, bzw (x, y))

Maximale LOOP-berechenbare Zahlen

Sei P ein LOOP-Programm

Seien x0, . . . , xk die in P vorkommenden Variablen.

Sei

fP(n) = max ( _k

X

i=0

ρ⁰(xi)|

k

X

i=0

ρ(xi)≤n,(ρ, P)−−−→

LOOP

∗ (ρ⁰, ε) )

f_P(n) ist die maximale Zahl, die als Summe aller

Endbelegungen ρ⁰ der Variablenx0, . . . , xk zustande kommt,

¨uber alle initialen Variablenbelegung ρ, die in der Summe der Werte ρ(x₀), . . . , ρ(x_k)den Wert n nicht ¨uberschreiten.

Maximale LOOP-berechenbare Zahlen (2)

Satz

F¨ur jedes LOOP-Programm P gibt es eine Konstantek, so dass fP(n)< a(k, n)f¨ur alle n∈N.

Beweis: NormalisiereP zun¨achst:

Ersetze Zuweisungenx_i:=x_j+c durch xi:=xj + 1;xi:=xi+ 1;. . . xi :=xi+ 1

| {z }

c−1mal

.

F¨urLOOP x_i DO QEND und x_i kommt in Qvor:

Ersetze LOOPxi DO QEND durch x⁰_i:=x_i;LOOPx⁰_i DO QEND;x⁰_i := 0, wobei x⁰_i eine neue Variable ist.

Beides ver¨andertf_P nicht!

Zeige Behauptung f¨ur normalisierte Programme.

Maximale LOOP-berechenbare Zahlen (3)

Zu zeigen: F¨ur jedes normalisierte LOOP-Programm P gibt es eine Konstantek, so dassf_P(n)< a(k, n) f¨ur alle n∈N.

Beweis durch strukturelle Induktion ¨uber normalisiertes Programm. F¨alle:

1 Zuweisung xi :=xj+cmit c∈Zund c≤1

2 Sequenz P₁;P₂

3 LOOP-Schleife LOOPx_i DO QEND, wobei x_i nicht inQvorkommt.

Maximale LOOP-berechenbare Zahlen (3)

Zu zeigen: F¨ur jedes normalisierte LOOP-Programm P gibt es eine Konstantek, so dassf_P(n)< a(k, n) f¨ur alle n∈N.

Beweis durch strukturelle Induktion ¨uber normalisiertes Programm.

F¨alle:

1 Zuweisung xi :=xj+cmit c∈Zund c≤1

2 Sequenz P₁;P₂

3 LOOP-Schleife LOOPx_i DO QEND, wobei x_i nicht inQvorkommt.

Maximale LOOP-berechenbare Zahlen (3)

Zu zeigen: F¨ur jedes normalisierte LOOP-Programm P gibt es eine Konstantek, so dassf_P(n)< a(k, n) f¨ur alle n∈N.

Beweis durch strukturelle Induktion ¨uber normalisiertes Programm.

F¨alle:

1 Zuweisung xi :=xj+cmitc∈Zund c≤1

2 Sequenz P₁;P₂

3 LOOP-Schleife LOOPx_i DO QEND, wobei xi nicht inQvorkommt.

Maximale LOOP-berechenbare Zahlen (4)

Fall: Zuweisungx_i :=x_j+cmitc∈Z und c≤1 Dann giltfP(n)≤2n+ 1, da im maximalen Fall:

ρ(x_k) = 0 f¨urk6=j ρ(xj) =n

c= 1und ρ⁰(x_i) =n+ 1, ρ⁰(xj) =nund

ρ⁰(x_k) = 0 f¨urk6=j und k6=i Mita(2, y) = 2y+ 3(s. Skript) folgt

f_P(n)≤2n+ 1<2n+ 3 =a(2, n) D.h. die Aussagef_P(n)≤a(k, n) gilt mit k= 2.

Maximale LOOP-berechenbare Zahlen (5)

Fall: SequenzP₁;P₂

Induktionsannahme:f_Pi(n)< a(k_i, n) f¨uri= 1,2.

Es gilt:

f_P(n) =f_P2(f_P1(n))

< a(k2, a(k1, n))

≤a(max{k₁, k2}, a(max{k₁, k2}, n) (1)

≤a(max{k₁, k₂}, a(max{k₁, k₂}+ 1, n+ 1) (1)

=a(max{k₁, k₂}+ 1, n+ 1) (Definition vona)

≤a(max{k₁, k2}+ 2, n) (2)

(1) Monotonie:x≤x⁰, y ≤y⁰ =⇒ a(x, y)≤a(x⁰, y⁰) (2) Monotonie:a(x, y+ 1)≤a(x+ 1, y)

Daher giltf_P(n)< a(k, n) f¨ur k= max{k₁, k2}+ 2.

Maximale LOOP-berechenbare Zahlen (6)

Fall:LOOP x_i DO QEND und x_i kommt nicht inQ vor Induktionsannahme:f_Q(n)< a(k_Q, n) f¨ur eink_Q.

fP(n) berechnet Maximum. Sei ρ so, dass fP(n) maximal ist.

Wenn ρ(xi) = 0, dann istfP(n) =n < a(0, n).

Wenn ρ(x_i) = 1, dann istf_P(n) =f_Q(n)< a(k_Q, n) Sei ρ(x_i)≥2. . . .

Maximale LOOP-berechenbare Zahlen (7)

Fall:LOOP x_i DO QEND und x_i kommt nicht inQ vor Sei ρ(xi)≥2. . . . Da xi nicht inQ vorkommt, gilt:

f_P(n) =f_Q(. . .(f_Q

| {z }

ρ(xi)mal

(n−ρ(x_i)). . .) +ρ(x_i) (daxi6∈Q,fQ unabh. vonρ(xi))

≤a(k1, . . . , a(k1, n−ρ(xi)). . .) (ρ(xi)-mal gilt<(f¨ur jedesfQ).

Daher ≤undρ(x_i)f¨allt weg)

< a(k1, . . . , a(k1,

| {z }

ρ(xi)−1mal

a(k1+ 1, n−ρ(xi)). . .))(1)

=a(k1+ 1, n−ρ(xi) +ρ(xi)−1)(Definition vona)

=a(k1+ 1, n−1)≤a(k1+ 1, n)(2)

(1) Monotonie:a(x, y)< a(x+ 1, y) (2) Monotonie:a(x, y)< a(x, y+ 1) Daher giltf_P(n)< a(k, n) f¨ur k=k₁+ 1

Ackermannfunktion nicht LOOP-berechenbar

Theorem

Die Ackermannfunktion ist nicht LOOP-berechenbar.

Beweis:

Annahme: aist LOOP-berechenbar.

Dann ist auchf(x1) =a(x1, x1) LOOP-berechenbar.

Sei P LOOP-Programm, dassf berechnet.

Dann gilt f(x₁)≤f_P(x₁) (daρ⁰(x₀) =f(x₁) nach Ausf¨uhrung von P)

Es gibt Konstante k, sodassf_P(n)< a(k, n) Starte P mitρ={x₁ 7→k}.

Dann gilt f(k)≤f_P(k)< a(k, k) =f(k) Widerspruch!

aist nicht LOOP-berechenbar.

Fazit

Theorem

Es gibt totale WHILE-berechenbare (bzw. GOTO-berechenbare, Turingberechenbare) Funktionen, die nicht LOOP-berechenbar sind.

Rekursive Funktionen

Weiterer Formalismus zur Definition der Berechenbarkeit Primitiv rekursive Funktionen und

µ-rekursive Funktionen Wir werden sehen

Primitiv rekursive Funktionen entsprechen genau den LOOP-berechenbaren Funktionen

µ-rekursive Funktionen entsprechen genau den

Turingberechenbaren (WHILE-, GOTO-berechenbaren) Funktionen

Primitiv rekursive Funktionen

Definition

Eine Funktionf :N^k→Nistprimitiv rekursiv, wenn sie der folgenden induktiven Definition gen¨ugt:

Jedekonstante Funktionf(x1, . . . , x_k) =c∈Nist primitiv rekursiv.

DieProjektionsfunktionenπ^k_i(x₁, . . . , x_k) =x_isind primitiv rekursiv.

DieNachfolgerfunktionsucc(x) =x+ 1ist primitiv rekursiv.

Komposition / Einsetzung: Wenng:N^m→Nund f¨uri= 1, . . . , m:

h_i:N^k→Nprimitiv rekursiv sind, dann ist auchf mit

f(x₁, . . . , x_k) =g(h₁(x₁, . . . , x_k), . . . , h_m(x₁, . . . , x_k))primitiv rekursiv.

Primitive Rekursion: Wenng:N^k−1→Nundh:N^k+1→Nprimitiv rekursiv, dann ist auchf mit

f(x₁, . . . , x_k) =

g(x₂, . . . , x_k), wennx₁= 0

h(f(x₁−1, x₂, . . . , x_k), x₁−1, x₂, . . . , x_k),sonst primitiv rekursiv.

Konstruktionen

Komponenten eines Tupels entfernen / vertauschen / vervielfachen Wenng:N⁴ →Nprimitiv rekursiv, dann ist auchf :N³→N mit

f(n1, n2, n3) =g(n2, n3, n3, n2), denn:

f(n₁, n₂, n₃) =g(π³₂(n₁, n₂, n₃), π³₃(n₁, n₂, n₃), π³₃(n₁, n₂, n₃), π₂³(n₁, n₂, n₃))

Konstruktionen (2)

Rekursion durch das i. Argument F¨ur1≤i≤kkann man

f(x₁, . . . , x_k) =







g(x₁, . . . , x_i−1, x_i+1, x_k),fallsx_i= 0

h(f(x₁, . . . , xi−1, x_i−1, x_i+1, . . . , x_k), x₁, . . . ,

xi−1, x_i−1, x_i+1, . . . , x_k),sonst durchf(x1, . . . , x_k) =f⁰(xi, x1. . . , xi−1, xi+1, . . . , x_k)darstellen, wobei

f⁰(x₁, . . . , x_k) =

g⁰(x₂, . . . , x_k),fallsx₁= 0

h⁰(f⁰(x₁−1, x₂. . . , x_k), x₁−1, x₂, . . . , x_k),sonst g⁰(x1, . . . , xk−1) = g(x2, . . . , xi, x1, xi+1, . . . , x_k)

h⁰(x₁, . . . , x_k+1) = h(x₁, x₂, . . . , x_i, x₁−1, x_i+1, . . . , x_k)

Beispiele (1)

Additionsfunktion

add(x1, x2) =x1+x2 ist primitiv rekursiv:

add(x₁, x₂) =

x2, fallsx1= 0

succ(add(x₁−1, x₂)), sonst Bemerkung:

Die verwendeten Funktioneng und h aus der Definition der primitiv rekursiven Funktionen sind hier:

g=π₁¹

h(x1, x2, x3) =succ(π₁³(x1, x2, x3))

Beispiele (2)

Multiplikationsfunktion

mult(x₁, x₂) =

0, fallsx₁= 0

add(mult(x1−1, x2), x2), sonst Idee:x1-malx2 zu0 addieren:

Beispiele (3)

Differenz

Allgemeinx₁−x₂ nicht primitiv rekursiv, undefinierter Fall x₁ < x₂ nicht darstellbar.

Angepasste Differenz

liefert0falls x1 < x2, ist primitiv rekursiv:

sub(x₁, x₂) =

x₁, falls x₂ = 0

pred(sub(x₁, x₂−1)) sonst wobei

pred(x₁) =

0, falls x₁ = 0 x₁−1, sonst

N¨ achstes Ziel

Wir wollen zeigen:

Primitiv rekursive Funktionen sind genau die LOOP-berechenbaren Funktionen

Ben¨otigt:

Darstellung der Variablenbelegung ρ alseine einzige Zahl, um sie der primitiv rekursiven Funktion als Argument zu

¨

ubergeben.

D.h. eindeutige Darstellung eines Tupels nat¨urlicher Zahlen als eine einzige Zahl.

Operationen zum Konvertieren in beide Richtungen Eine solches Verfahren nennt man auch

”G¨odelisierung“

(nach Kurt G¨odel)

G¨ odelisierung (1)

Tupel von nat¨urlichen Zahlen(x₀, . . . , x_k) bijektiv in die nat¨urlichen Zahlen abbilden

F¨ur festes k

mit primitiv rekursivenFunktionen c(x, y) =

x+y+ 1 2

+x Werte vonc(x, y) f¨ur x, y∈ {0, . . . ,5}:

y\x 0 1 2 3 4 5

0 0 1 3 6 10 15

1 2 4 7 11 16 22

2 5 8 12 17 23 30

3 9 13 18 24 31 39

4 14 19 25 32 40 49

5 20 26 33 41 50 60

G¨ odelisierung (2)

Funktionc ist primitiv rekursiv, da 0

2

= 0 und

n+ 1 2

= n

2

+n

F¨urk+ 1-Tupel definieren wir:

hx₀, . . . , xki=c(x0, c(x1, . . . , c(xk,0). . .)) Beachte:h·i ist primitiv rekursiv

(dacprimitiv rekursiv und Komposition primitiv rekursiv)

G¨ odelisierung (3)

R¨uckgewinnung der Komponenten:

Seienleft und right Funktionen mit left(c(x, y)) =x und

right(c(x, y)) =y.

Im Skript wird gezeigt:

left und right existieren

left und right sind primitiv rekursiv

G¨ odelisierung (5)

Zugriff auf beliebige Komponenten:

Programmiered_i(hx₀, . . . , x_ki) =x_i durch:

d₀(x) = left(x) d1(x) = left(right(x))

di(x) = left(right(right. . .right

| {z }

imal

(x). . .))

Damit sind auch died_i-Funktionen primitiv rekursiv.

Von LOOP-Programm berechnete Funktion

Sei P ein LOOP-Programm, ρ eine Variablenbelegung mit (ρ, P)−−−→

LOOP

∗ (ρ⁰, ε)

Seien x0, x1, . . . , xn alle vom ProgrammP verwendeten Variablen (auch solche, die nicht in ρ vorkommen) Die vonP berechnete Funktion:

gP(hx₀, . . . , xni) =hx⁰₀, . . . , x⁰_ni (wobei x⁰_i =ρ⁰(xi))

LOOP-Programme berechnen primitiv rekursive Funktionen

Lemma

F¨ur jedes LOOP-Programm P ist die zugeh¨orige FunktiongP

primitiv rekursiv.

Beweis: Strukturelle Induktion ¨uber jedes TeilprogrammQund die zugeh¨orige Funktiong_Q.

Basis:Q ist Zuweisungx_i =x_j±c.

F¨urgQ muss gelten:

gQ(hm₀, . . . , mni) =hm₀, . . . , mi−1, mj±c, mi, . . . , mni Primitiv rekursive Implementierung:

g_Q(x) =hd₀(x), . . . , di−1(x), d_j(x) +c, d_i+1(x), . . . d_n(x)i

LOOP-Programme berechnen primitiv rekursive Funktionen (2)

Induktionsschritt:

Q ist eine SequenzQ₁;Q₂.

Induktionshypothese: primitiv rekursive Funktionen g_Q1,g_Q2. Funktion g_Q(x) =g_Q2(g_Q1(x))ist primitiv rekursiv.

Q istLOOP xi DOP END.

Induktionshypothese liefert primitiv rekursive Funktion gP. Konstruktion von g_Q:x_i-mal wirdg_P angewendet.

gQ(x) = run(di(x), x) run(n, x) =

x, fallsn= 0

gP(run(n−1, x)) sonst

run ist primitiv rekursiv. Damit auch g_Q primitiv rekursiv.

LOOP-berechenbare Funktionen sind primitiv rekursiv

Satz 11.1.6

Jede LOOP-berechenbare Funktion ist primitiv rekursiv.

Beweis:

Sei f :N^k→N LOOP-berechenbar.

Sei P LOOP-Programm mit ρ={x₁ 7→n₁, . . . , x_k7→n_k}, (ρ, P)−−−→

LOOP

∗ (ρ⁰, ε) undρ⁰(x0) =f(n1, . . . , nk)

Es gilt f(n₁, . . . , n_k) =d₀(g_P(h0, n₁, . . . , n_k,0, . . . ,0i)).

Dah·i,d₀ und g_P primitiv rekursiv sind, ist auch f primitiv rekursiv.

Primitiv rekursive Funktionen sind LOOP-berechenbar

Satz 11.1.7

Jede primitiv rekursive Funktion ist LOOP-berechenbar.

Beweis: Induktion ¨uber Struktur der primitiv rekursiven Funktion:

Wenn f(x) =c,f =succ, oderf =π_n^k, dann gibt es auch LOOP-Programm dazu.

Wenn f(x1, . . . , x_k) =h(g1(x1, . . . , x_k), . . . , gn(x1, . . . , x_k)):

Induktionshypothese liefert LOOP-ProgrammeP_h und Pg,1, . . . , Pg,n, dieh,g1,. . . ,gn berechnen.

Konstruiere Programm f¨ur f nach dem Schema:

y1 :=g1(x1, . . . , x_k);. . .;yn:=gn(x1, . . . , x_k);x0 :=h(y1, . . . , yn) Genauer: Pg,1, . . . , Pg,n, P_h ab¨andern, so dass sie auf

disjunkten Variablenmengen arbeiten, entsprechende Variableninhalte f¨urx1, . . . , xk verdoppeln.

. . .

Primitiv rekursive Funktionen sind LOOP-berechenbar (2)

. . .

f ist primitiv rekursiv:

f(x₁, . . . , x_k) =

g(x₂, . . . , x_k) wenn x₁= 0

h(f(x₁−1, x₂, . . . , x_k), x₁−1, x₂, . . . , x_k) sonst wobei g:N^k−1 →Nund h:N^k+1→N primitiv rekursiv sind.

Induktionshypothese liefert LOOP-Programme, die g, h berechnen.

Konstruiere LOOP-Programm f¨ur f nach dem Schema y:= 0;

x₀ :=g(x₂, . . . , x_k);

LOOPx₁ DO y:=y+ 1;x₀ :=h(x₀, y, x₂, . . . , x_k) END

LOOP-berechenbar = primitiv rekursiv

Theorem 11.1.8

Die primitiv rekursiven Funktionen sind genau die LOOP-berechenbaren Funktionen.

µ-Operator

Definition µ-Operator

Seih:N^k+1 →Neine (partielle oder totale) Funktion. Dann ist (µh) :N^k→Ndefiniert als

(µh)(x1, . . . , xk) =











n fallsh(n, x₁, . . . , x_k)= 0 und f¨ur allem <n:h(m, x₁, . . . , x_k)ist definiert und h(m, x1, . . . , x_k)>0.

undefiniert, sonst µ-Operator

”sucht“ nach einer kleinsten Nullstelle von h.

Wenn diese nicht existiert (entweder da h keine Nullstelle hat, oder da h undefiniert ist f¨ur Werte, die kleiner als die Nullstelle sind), dann ist auch der µ-Operator angewendet auf hundefiniert.

µ-rekursive Funktionen

Definition

Die Menge allerµ-rekursiven Funktionensei die kleinste Menge, so dass gilt:

Jedekonstante Funktionf(x₁, . . . , x_k) =c∈Nistµ-rekursiv.

DieProjektionsfunktionenπ^k_i(x₁, . . . , x_k) =x_isindµ-rekursiv.

DieNachfolgerfunktionsucc(x) =x+ 1istµ-rekursiv.

Komposition / Einsetzung: Wenng:N^m→Nund f¨uri= 1, . . . , m:

h_i:N^k→Nµ-rekursiv sind, dann ist auchf mit

f(x₁, . . . , x_k) =g(h₁(x₁, . . . , x_k), . . . , h_m(x₁, . . . , x_k))µ-rekursiv.

Rekursion: Wenng:N^k−1→Nundh:N^k+1→Nµ-rekursiv, dann ist

f(x₁, . . . , x_k) =

g(x₂, . . . , x_k), wennx₁= 0

h(f(x₁−1, x₂, . . . , x_k), x₁−1, x₂, . . . , x_k),sonst auchµ-rekursiv.

µ-Operator: Wennh:N^k+1→Nµ-rekursiv, dann auchf =µh µ-rekursiv.

WHILE-berechenbare Funktionen sind µ-rekursiv

Satz 11.2.3

Jede WHILE-berechenbare Funktion istµ-rekursiv.

Beweis: Analog zu Satz 11.1.6 ¨uber Struktur des WHILE-ProgrammsP Neuer Fall:P ist WHILEx_i6= 0 DO QEND

Induktionshypothese liefertµ-rekursive Funktion gQ f¨urQ.

Konstruiere:

g_P(x) = run(µ(run_i)(x), x) runi(n, x) = di(run(n, x)) run(n, x) =

x, fallsn= 0

g_Q(run(n−1, x)) sonst run(n, x) f¨uhrt n-malg_Q aus.

µ(run_i)(x) berechnet, wie oft die Schleife minimal durchlaufen werden muss, bis x_i den Wert 0 hat .

Divergiert die Schleife, so istµ(run_i) undefiniert undg_P undefiniert.

µ-rekursive Funktionen sind WHILE-berechenbar

Satz 11.2.4

Jedeµ-rekursive Funktion ist WHILE-berechenbar.

Beweis: Analog zu Satz 11.1.7 ¨uber die Struktur der Funktion.

Neuer Fall:f =µh f¨ur eine µ-rek. Funktionh.

Induktionshypothese liefert WHILE-ProgrammP_h, dash berechnet.

KonstruierePf nach dem Schema:

x₀ := 0;

y:=h(0, x₁, . . . , x_n);

WHILE y6= 0 DO

x₀:=x₀+ 1;y:=h(x₀, . . . , x_n) END

WHILE-Schleife berechnet minimalen Wert f¨ur h(x0, . . . , xn) = 0 Wenn dieser nicht existiert, terminiert die Schleife nicht.

Entspricht der Berechnung vonµh.

WHILE-berechenbar = µ-rekursiv

Theorem 11.2.5

Dieµ-rekursiven Funktionen entsprechen genau den WHILE-berechenbaren (und damit auch den GOTO- und Turingberechenbaren) Funktionen.

Uberblick: Berechenbarkeitsformalismen ¨

WHILE-berechenbar

LOOP-berechenbar primitiv rekursiv

µ-rekursiv

Turingberechenbar GOTO-berechenbar

Theorem 11.1.8 Theorem 11.2.4

Satz 10.5.2

Theorem 10.2.4 Theorem 10.4.1

Satz 10.2.3