Vorlesungsskript Statistische Mechanik

Statistische Mechanik

Thomas Lauermann und Raphael Straub

21. Februar 2006

1 Vorbetrachtungen 5

1.1 Wahrscheinlichkeitstheorie . . . 5

1.1.1 Definitionen . . . 5

1.1.2 Der Zentrale Grenzwertsatz . . . 10

1.2 Quantenstatistik . . . 12

1.2.1 Wiederholung der Quantenmechanik vieler Freiheitsgrade . . . 12

1.2.2 statistischer Dichteoperator; reine Zust¨ande & Gemische . . . 14

1.2.3 (Un-)abh¨angige Subsysteme . . . 18

1.2.4 Von-Neumann-Gleichung . . . 22

1.3 Klassische Statistik . . . 23

1.3.1 Der Phasenraum . . . 23

1.3.2 Liouville-Theorem und Liouville-Gleichung . . . 24

1.4 Wichtige Gesamtheiten (Ensemble) . . . 26

1.4.1 Das Beispiel paramagnetischer Salze . . . 26

1.4.2 Der kanonische Dichteoperator . . . 26

1.4.3 Fortsetzung des Curie-Paramagnetismus . . . 28

1.4.4 Das klassische monoatomare ideale Gas . . . 37

1.4.5 Mikrokanonischer Dichteoperator / Wahrscheinlichkeitsdichte . . . . 37

1.4.6 Fortsetzung: ideales Gas . . . 39

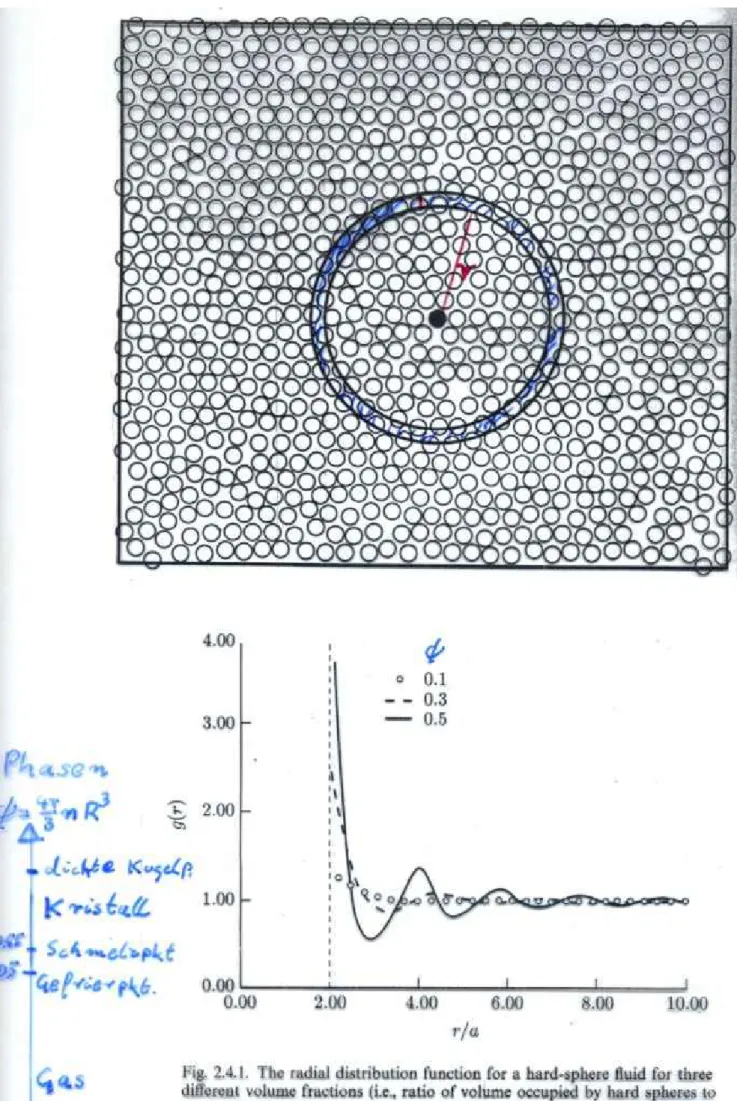
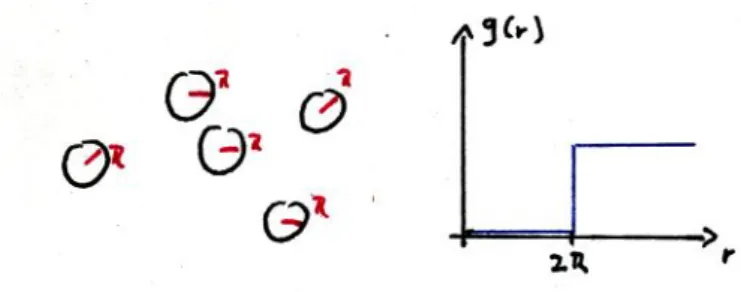
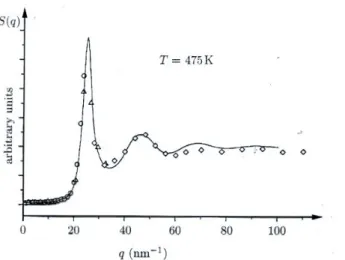
1.5 Korrelationsfunktionen und Strukturfaktoren . . . 42

1.5.1 Motivation . . . 42

1.5.2 Dichtefluktuationen f¨ur den klassischen Fall . . . 43

1.5.3 Schwankungen makroskopischer additiver Gr¨oßen . . . 53

2 Konzepte & Postulate der statistischen Mechnik 55 2.1 thermisches Gleichgewicht . . . 55

2.1.1 Systeme . . . 55

2.1.2 Thermisches Gleichgewicht . . . 57

2.1.3 Postulat: ’gleiche apriori Wahrscheinlichkeit’ (Laplace) . . . 57

2.1.4 Boltzmann Entropie . . . 61

2.1.5 Kanonische Gesamtheit . . . 62

2.2 Die verallgemeinerte großkanonische Gesamtheit . . . 67

2.2.1 Beipiele großkanonischer Gesamtheiten . . . 69

2.3 Gibbssche Entropieformel und Informationsentropie . . . 73

2.3.1 Additivit¨at . . . 74

2.3.2 Kleinsche Ungleichung . . . 75

2.3.3 Mikrokanonische Gesamtheit . . . 76

2.3.4 Kanonische Gesamtheit . . . 76 3

2.3.5 Partielle Gleichgewichte in der verallgemeinerten Großkanonischen

Gesamtheit . . . 77

2.3.6 Zeitabh¨angigkeit der Entropieen . . . 80

3 Thermodynamik 81 3.1 0ter Hauptsatz & Temperatur . . . 81

3.2 1ter Hauptsatz, Arbeit & W¨arme . . . 82

3.3 2ter Hauptsatz & Irresibilit¨at . . . 83

3.4 3ter Hauptsatz & absoluter Nullpunkt . . . 86

3.5 Thermodynamischer Limes . . . 87

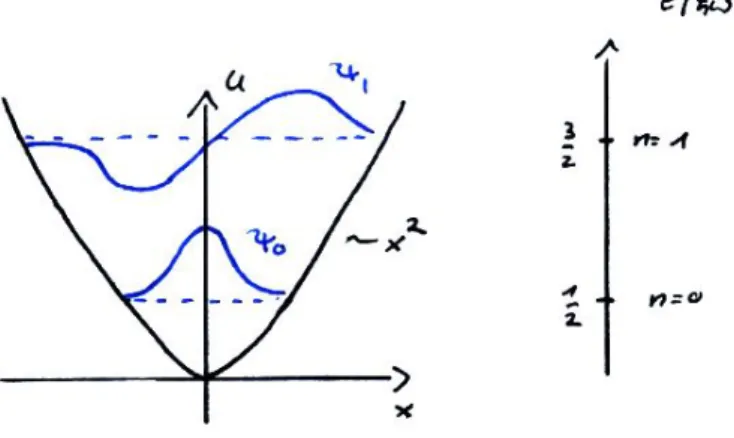
4 Quantengase 91 4.0 Erinnerung an die Zustandssumme des harmonischen Oszillators . . . 91

4.1 Ununterscheidbarkeit und Quantenstatistik . . . 93

4.1.1 Das Pauli-Prinzip . . . 94

4.1.2 Besetzungszahlen n & Großkanonische Gesamtheit . . . 95

4.1.3 Die Fermi-Dirac- und Bose-Einstein-Verteilungsfunktion . . . 99

4.2 Fast Entartetes Fermi-Gas . . . 103

4.3 Bose-Gase . . . 106

4.3.1 chemisches Potential nicht-erhaltener Teilchen . . . 106

4.3.2 Photonen . . . 107

4.3.3 Bose-Einstein-Kondensation . . . 109

5 Wechselwirkende Systeme und Phasen¨uberg¨ange 115 5.1 Uberblick . . . 115¨

5.2 Perturbative N¨aherungsverfahren . . . 120

5.2.1 Das Potential der mittleren Arbeit . . . 120

5.2.2 Die Virialentwicklung . . . 123

5.3 Selbstkonsistente Variationserfahren . . . 125

5.3.1 Molekularfeld-Theorie . . . 125

5.3.2 Anwendung auf das Ising-Modell . . . 126

5.4 Isingartige Phasen¨uberg¨ange . . . 132

5.4.1 Existenz geordneter Phasen . . . 132

5.4.2 Spontane Symmetriebrechung . . . 133

5.4.3 Universalit¨at . . . 133

Vorbetrachtungen

1.1 Wahrscheinlichkeitstheorie

siehe Skript zum IK IV Sommersemester 2005 (http:

huygens.physik.uni-konstanz.de)

1.1.1 Definitionen

n Gr¨oßen ξi, i = 1. . . n bilden einen reellen n-dimensionalen Zufallsvektor ξ, wenn die Wahrscheinlichkeit, dass ξ Werte im Bereich [x , x+ dx] annimmt, gegeben ist durch P_n(x) dx₁ · · · dx_n =P_n(x) dⁿx, wobei diegemeinsame Wahrscheinlichkeitsdichte erf¨ullen muss:

• i) P_n(x)≥0 Die Wahrscheinlichkeit ist nicht negativ

• ii) R

dⁿxP_n(x) = 1 (Normierung) wobei R

dⁿx· · ·=

∞

R

−∞

dx₁

∞

R

−∞

dx₂· · ·

∞

R

−∞

dx_n· · · Bemerkungen:

• Die Menge aller m¨oglichen Wertex (Ereignisse) heißt Ereignismenge.

• Diskrete Wertex^α ∈

x⁽¹⁾, . . . ,x^(N) (d.h.N m¨ogliche Werte) k¨onnen durchDirac- Delta-Maße wie folgt beschrieben werden:

P_n(x) =

N

X

α=1

P_αδ(x−x^α) (1.1)

mit Pα ≥0 und

N

P

α=1

Pα = 1 Definitionen wichtiger Gr¨oßen:

• Mittelwert:

ξ

= Z

dⁿx xPn(x) = ¯ξ (1.2)

5

• totales Schwankungsquadrat (Varianz):

σ² : = ∆ξ² :=

(ξ−¯ξ)²

=

N

X

i=1

Z

dⁿx x_i−ξ¯_i2

P_n(vex)

=

N

X

i=1

Z

dⁿx

x²_i −2x_iξ¯_i+ ¯ξ_i²

P_n(x) (1.3)

= ξ²

− ξ2

P(x) dx ist die Wahrscheinlichkeit f¨urξ Werte in [x,x+ dx] anzunehmen. Diese ist messbar durch die relative H¨aufigkeit:

Z (Messungen von x in [x,x+ dx]) Gesamtzahl der Messungen =W f¨ur viele Messungen.

• Einzel-Varianz:

σ_i² =

(ξ_i −ξ¯_i)²

• (relative) Streuung:

σ

|¯ξ|

• Korrelation:

K_ij =

ξ_i−ξ¯_i

· ξ_j−ξ¯_j

= Z

dⁿx x_i−ξ¯_i

· x_j −ξ¯_j

P_n(x) = K_ji (1.4) Bemerkungen:

– Die Korrelation ist eine symmetrische Matrix und hat somit (vgl. lineare Alge- bra) reelle Eigenwerte. Ihre Eigenvektoren bilden ein Orthogonalsystem. Dies bedeutet wiederum, dass lineare Transformationen der ξi auf ξ_i⁰ = P

i

Ajiξi

existieren, so dass die Matrix:

K⁰ =A^T K A diagonal ist.

– K ist positiv definit, d.h. f¨ur einen beliebigen Vektor a ∈ Rⁿ ist folgendes erf¨ullt:

0≤

N

X

ij=1

a_iK_ija_j (1.5)

Beweis:

Es muss auf jeden Fall gelten:

X

ij

a_i

ξ_i−ξ¯_i

ξ_j−ξ¯_j

a_j = A²

≥0

wobei A=A(ξ) =

n

P

i=1

a_i(ξ_i−xi¯_i).

Durch geschickte Wahl vonA kann man daraus folgern:

∗ i) Wir w¨ahlen zun¨achsta_i =δ_ii0 d.h. der Vektora ist ausser an der i₀-ten Komponente (wo er 1 ist) Null. dann folgt trivialerweise:

K_i0i0 =D

ξ_i0 −ξ¯_i02E

=σ²_i0 ≥0

∗ ii) Sind die Komponenteni₁ und i₀ vona Eins und alle anderen Null, d.h.

a_i =δ_ii0 ±δ_ii1, so folgt:

K_i0i0 +K_i1i1 ±2K_i0i1 ≥0

Dies bedeutet, dass dieKreuzkorrelationen kleiner sind, als dieSelbstkor- relationen:

|K_i0i1| ≤ 1

2(K_i0i1 +K_i1i1)

– Aus den obigen ¨Uberlegungen ergibt sich auch der Zusammenhang mit der Varianz als Summe der Selbstkorrelationen zu:

σ² =

n

X

i=1

K_ii = SpK (1.6)

• Die charakteristische Funktion ist f¨ur k∈Rⁿ definiert ¨uber:

ϕ(k) =

exp{ik·ξ}

= Z

dⁿxexp{ik·x}P_n(x) (1.7) Sie ist also die Fourier-Transformierte von P_n(x).

Im Folgenden wollen wir zur Vereinfachung diese charrakteristische Funktion im Eindimensionalen betrachten.

• ϕ(k) heißt auch Momentengenerierende, wobei das m-te Moment lautet:

hξ^mi= Z

dx x^mP(x) (1.8)

Falls die Momente existieren, d.h. | hξ^mi | ≤ ∞, gilt:

ϕ(k) =hexpikξi=

∞

X

m=0

1

m!(ik)^mhξ^mi (1.9)

also berechnet sich das m-te Moment aus:

hξ^mi=

−i ∂

∂k m

lnϕ(k) k=0

• ϕ(k) bestimmt die sogenannten Kummulanten ¨uber:

ϕ(k) = exp

∞

X

m=1

(ik)^m m! hξ^mi_c

| {z }

∗

(1.10)

Dabei ist * die m-te Kummulante. Diese ist eine geschickte Kombination aller mo- mente mit Ordnung m⁰ < m. F¨ur die ersten drei Kummulanten gilt:

ξ⁽¹⁾

c =hξi= ¯ξ ξ⁽²⁾

c =hξi − hξi² =σ² ξ⁽³⁾

c = ξ³

−3 ξ²

hξi+ 2hξi³ ...

Die erste Kummulante ist also der Mittelwert, die zweite die Varianz.

Beweis:

Durch Taylorreihenentwicklung um k = 0

ϕ(k) = 1 +ikhξi − 1

2k²hξ²i − i

6k³hξ³i+... (1.11)

ϕ(k) = exp

ikhξ¹i_C −k²

2 hξ²i_C− i

6hξ³i_C +...

(1.12)

= 1 +ikhξ¹i_C − 1

2k² hξ²i_C +hξ¹i²_C

− i

6k³ hξ³i_C+ 3hξ²i_Chξ¹i_C +hξ¹i³_C

+O(k⁴) Vergleichen wir nun die k-Ordnungen:

hξ¹iC = hξi

hξ²i_C = hξ²i − hξi² =σ²

hξ³i_C = hξ³i+ 3hξi²hξi −3hξ²ihξi − hξ³i

Kumulanten charakterisieren Wahrscheinlichkeitsdichten pr¨aziser als Momente.

• Variablentransformationen:

Sei die Zufallsvariableη eine Funktion derξ,η=f(ξ), dann ist die Wahrscheinlich- keit, dass η Werte im Intervall [y, y+ dy] annimmt, gegeben durch

P_η(y) = hδ(y−f(ξ))i= Z

dⁿx δ(y−f(x))P_ηξ(x) (1.13)

Damit haben wir:

P_η(y) dy = Z

∗

dⁿxP_n(x)

*: Werte von x, so dassx≤f(x)≤y+ dy.

Beispiel:

Wir betrachten die Summe ζ = ξ + η zweier Zufallsvariablen mit gemeinsamer Wahrscheinlichkeitsdichte P_z(x,y)

P_ζ(z) =hδ(z−f(ξ+η))i= Z

dx dy P_z(x,y)δ(z−x−y) (1.14) was zu einer einfachen Bezeichnung der charakteristischen Funktion f¨uhrt:

ϕ_ζ(k) = he^ikζi= Z

dz e^ikzP_ζ(z) (1.15)

= Z

dx dy dz e^ikzPz(x,y)δ(z−x−y)

= Z

dx dy e^ik(x+y)P_z(x,y) Dies kann man auch schreiben als:

ϕ_ζ(k) = ϕ_ξ,η,2

k= k_x

k_y k k

(1.16) wobei ϕ_ξ,η,2(k) =

Z

dx dy e^ikxx+ikyyP_z(x,y) (1.17) Definition:

Zwei Untermengen {ξ₁, ... ξ_r}und {ξ_r+1, ... ξ_n}mit 1< r < n von Zufallsvariablen heißen unabh¨angig, wenn gilt:

P_n(x₁... x_n) = P_r(x₁... x_r)·P_n−r(x_r+1... x_n) (1.18) Satz:

Die Korrelationen zwischen unabh¨angigen Variablen verschwinden, d.h. sie sind unkor- reliert. Umgekehrt gilt allerdings nicht, dass unkorrelierte Variablen unabh¨angig sein m¨ussen.

Beweis:

Seien ξ_i und ξ_j aus den unabh¨angigen Untermengen, also 1 ≤ i ≤ r und r+ 1 ≤j ≤ n, dann folgt:

Kij = Z

dⁿx Pr(x1... xr)·Pn−r(xr+1... xn)·(xi−ξ_i)(xj −ξ_j) (1.19)

= Z

d^rx P_r(x)(x_i−ξ_i)

· Z

d^n−rx Pn−r(x)(x_j−ξ_j)

= 0 (Wobei hier die Notation von ¯ξ zuξ gewechselt hat.)

weil wegen der Definition von ξ beide große Klammern = 0 sind.

1.1.2 Der Zentrale Grenzwertsatz

Die Summe ζ_n = Pn

i=1ξ_i von n unabh¨angigen Zufallsvariablen ξ₁, ... , ξ_n mit endlichen Mittelwerten und endlichen Varianzen, d.h.

hξ_ii=ξ_i <∞ und

h(ξ_i−ξ_i)i=σ² <∞

(d.h. sowohl < ξ_i > als auch σ²_i existieren und sind betragsm¨assig kleiner als ∞), dann besitzt ζn f¨ur große n eine Gauss-verteilung:

P_ζ(z) = 1

p2πΣ²_n ·exp

−(z−ζ_n)² 2Σ²_n

(1.20) mit dem Mittelwert

ζ_n=

n

X

i=1

ξ_i und der Varianz

Σ²_n =

n

X

i=1

σ_i²

F¨ur (zur Vereinfachung) gleichverteilte ξ_i finden wir also eine sehr enge Verteilung mit verschwindender Streuung, weil Gleichverteilungζ_n =nξ und Σ²_n=nσ² bedeutet und die Streuung mit wachsendem n immer geringer wird:

Σ_n

|ζ_n| =

√n σ n|ζ| ∝ 1

√n (1.21)

Bemerkungen:

• Die Voraussetzungen waren: Unabh¨angige ξ_i und endliche Mittelwerte bzw. Vari- anzen, was zu einer Gaussverteilung mit ζ_n ∝ n und Σ²_n ∝ n f¨uhrt; d.h. dass 2 Kumulanten also die Wahrscheinlichkeitsdichte P_ζ festlegen.

• Der zentrale Grenzwertsatz ist wichtig f¨ur die statistische Mechanik und die Ther- modynamik, wo n im Bereich 10²³ liegt, da die dort auftretenden Mengen- (oder extensive) Gr¨oßen solche additiven Gr¨oßen sind. Wir haben also viele kleine un- abh¨angige Beitr¨age zu einer extensiven Gr¨oße.

Beispiele:

• Teilchenzahl N

• gesamte kinetische Energie E_kin =Pn i=1

p²_i 2mi

• die Gesamtenergie Ekin+Epot=E mit paarweiser Wechselwirkung E_pot =

N

X

i=1 i−1

X

j=1

U(|r_i−r_j|)

= 1

2

N

X

i,j=1

U(|r_i−r_j|) = 1 2

N

X

i=1

U_i(r_i,{r}) (1.22) mit U_i, der potentiellen Energie des i-ten Teilchens.

Der Zentrale Grenzwertsatz verlangt Unabh¨angigkeit, was in der Statistischen Mechanik durch Unkorreliertheit von Teilchen in großem Abstand, d.h.|r_i−r_j| ξ(die sogenannte Korrelationsl¨ange) beschrieben wird.

Wir betrachten nun drei F¨alle und untersuchen, wann die Statistische Mechanik ange- wandt werden kann und wann nicht:

• Fall A:Kurzreichweitige Potentiale und hohe Temperatur ⇒Statistische Mechanik und Gaussverteilung

• Fall B:Kurzreichweitige Potentiale und niedrige Temperatur⇒Statistische Mecha- nik aber keine Gaussverteilung

• Fall C:Langreichweitige Potentiale, z.B. Gravitation ⇒ Statistische Mechanik ver- sagt hier.

Beweis:

F¨ur (zur Vereinfachung) gleichverteilte, unabh¨angigeξ_i (mit ξ und σ²) betrachten wir η_n = 1

√n

n

X

i=1

(ξ_i−ξ) mit unabh¨angigen P_n.

ηn hat die Wahrscheinlichkeitsdichte:

P_η(y) = Z

dⁿx P_n(x)δ y− 1

√n

n

X

i=1

(x_i−ξ)

!

wobei der Mittelwert

ξ= Z

dx x P₁(x) ist und die Varianz

σ² = Z

dx(x−ξ)²P1(x)

Die charakteristische Funktion erf¨ullt also ϕ_η(k) =

Z

dy e^ikyP_η(y)

= Z

dx₁...dx_nP₁(x₁)... P₁(x_n)·exp ik

√n

n

X

i=1

(x_i−ξ)

!

=











 e^−ik√nξ·

Z

dx e^√iknxP₁(x)

| {z }

ϕξ(^√k_n)













n

(1.23)

Verwenden wir nun die Kumulanten von ϕξ(^√k_n):

ϕ_ξ( k

√n) = exp ik

√nξ− k²

2nσ²− ik³

6n^1,5hξ³i_C +...

so folgt (ξ f¨allt raus):

ϕ_η(k) = exp

−−k²

2 σ² +O(n⁻¹²)

n→inf ty

−→ e^−k

2σ2 2

und mit Fourier-R¨ucktransformation erhalten wir:

Pη(y) = Z dk

2π ·e^−ikye^k

2σ2

2 = 1

√

2πσ² ·e^−y

2 2σ2

Die Wahrscheinlichkeitsdichte von ξn =nξ+√

nηn folgt gem¨aß Variablentransformation P_ξ(z) =hδ(z−nξ−√

nη_n)i (1.24)

1.2 Quantenstatistik

1.2.1 Wiederholung der Quantenmechanik vieler Freiheitsgrade

M¨ogliche Zust¨ande |Ψi eines quantenmechanischen Systems von f Freiheitsgraden sind Elemente aus einem Hilbertraum H, also |Ψi ∈ H und sie sollen normiert sein:

hΨ|Ψi= 1

Der Hilbertraum H besitzt eine Orthonormalbasis bezeichnet mit {n₁, ... n_f}={|ni}

Die Zeitabh¨angigkeit ist gegeben durch die Schr¨odinger-Gleichung f¨ur den unit¨aren Zeitevolutionsoperator U:

i~∂_tU(t,t₀) = H(t)U(t,t₀)

mit U(t =t0,t0) = 1 (1.25)

wobei H(t) = H(t)^† der Hamilton-Operator ist.

In der Vorlesung IKIV wurden bereits die beiden BetrachtungsweisenSchr¨odinger- und Heisenberg-Bild eingef¨uhrt:

Ist ein Operator nicht von sich aus schon zeitabh¨angig, so bekommt er imSchr¨odinger- Bild keine Zeitabh¨angigkeit hinzu. Die Zeitabh¨angigkeit steckt hier in der Wellenfunktion:

|ψ(t)i=|ψ(t)i_S =U(t,t₀)|ψ(t₀)i (1.26) A_S(t) =A_S =A

Im Heisenberg-Bild dagegen tr¨agt der Operator die ganze Zeitabh¨angigkeit und die Wellenfunktion ist zeitlich konstant:

|ψ(t)i_H =|ψ(t₀)i (1.27)

A_H(t) = U⁻¹(t,t₀)A_S(t)U(t,t₀) (1.28) Zum Beweis betrachtet man die Ableitung des Heisenberg-Operators und erh¨alt:

d

dtA_H(t) = i

~

(HA_H −A_HH) + (∂_tA)_H = i

~

[H,A] + (∂_tA)_H

⇒ A_H(t) = e^iHt/~A_se^iHt/~

Beispiele:

• Ein freies Teilchen in einer Box mit dem Volumen V = L³ mit der periodischen Randbedingung f¨ur seine Wellenfunktion:

ψ(r+Lˆe) =ψ(r)

Seine Hamilton-Funktion bei drei Freiheitsgraden lautet:

H = p² 2m zu der Orthonormalbasis







k ; k = 2π L



 n_x ny

n_z



 ; n_i = 0,±1,±2, . . .







• F¨ur das Wasserstoffatom gilt mit den Indizes e f¨ur Elektron undp f¨ur Proton:

H = p²_p

2m_p + p²_e

2m_e − c

|r_e−r_p| mit der Orthonormalbasis

{|P ,n,l,mi}

wobei P der Schwerpunktsimpuls ist.

• Zwei nichtwechselwirkende Spins besitzen im Magnetfeld die Hamilton-Funktion:

H =−γ~ 2

σ1+σ

2

B(t) zu der Orthonormalbasis

{| ↑↑i=| ↑i1| ↑i2 ; | ↓↓i; | ↑↓i; | ↓↑i}

1.2.2 statistischer Dichteoperator; reine Zust¨ ande & Gemische

• (A) Erwartungswerte

Der hermitescheOperatorAaufHhat den Erwartungswerthψ|A|ψi=P

nn⁰

c^∗

n⁰c_n hn⁰|A|ni im reinen Zusatand |ψi, falls f¨ur diesen gilt:

|ψi=X

n

c_n |ni ∈ H (1.29)

Dabei sind die c_n seine Entwicklungskoeffizienten. In einem reinen Zustand lautet der Erwartungswert in Matrixdarstellung:

hψ|A|ψi= Sp (A|ψihψ|) = Sp (A%_ψ) (1.30) mit dem Dichteoperator eines reinen Zustands:

%_ψ :=|ψihψ| (1.31)

schreibt man:

hψ|A|ψi= Sp (A%_ψ)

Zum Beweis muss man die Spur von A%ψ in Matrix-Darstellung in der Orthonor- malbasis {|ni} ausrechnen:

Sp (A%_ψ) = X

n⁰

hn⁰|A%_ψ |n⁰i

Durch das Einf¨ugen der dyadischen Eins zwischen dem Operator A und dem Dich- teoperator %_ψ erh¨alt man:

Sp (A%_ψ) =X

n n⁰

hn⁰|A|ni

cn

z }| { hn|ψi

c^∗

n0

z }| { hψ|n⁰i

=X

n,n⁰

c_nc^∗_n0 hn⁰|A|ni

=X

n⁰

hn⁰|c^∗_n⁰|AX

n

c_n|ni

=hψ|A|ψi

• (B) Spurrechenregeln (zur Vereinfachung sei H endlich dimensional) Die Spur eines Operators ist definiert als:

SpA :=X

n

hn|A|ni

Es gelten die folgenden Rechenregeln:

– a) Die Spur ist invariant unter zyklischer Vertauschung:

Sp (AB) =X

n n⁰

hn|A|n⁰ihn⁰|B|ni= Sp (BA) Sp (ABC) = Sp (CAB) = Sp (BCA) – b) Invarianz unter Basiswechsel:

Geht man zu einer neuen Orthonormalbasis{|mi}˜ mit|mi˜ =P

n

U_{m n}|niuber,¨ wobei U der unit¨are Transformataionsoperator ist, so folgt mit der Tatsache, dass ˜A = U AU⁻¹ (vgl. U^†U AU⁻¹

| {z }

= ˜A

U = A sowie durch zweimaliges Einf¨uhren der dyadischen Eins: 1 =P

m

|mihm|:˜ SpA =X

n

hn|A|ni=X

n

hn|U^†A U˜ |ni

= X

n,m,˜ m˜⁰

hn|U^†|mi˜

| {z }

∗

hm|˜ A|˜m˜⁰i

| {z }

∗∗

hm˜⁰|U|ni=F

Der Term wird nun hinter die beiden anderen gestellt, so dass ** nach vorne rutscht.

MitP

n

hm˜⁰|U|nihn|U^†|mi˜ =δ_{m m}⁰ folgt weiter:

F=X

˜ m

hm|A|˜ mi˜

– c) Spur & Eigenwerte:

Die Spur eines diagonalisierbaren OperatorsAist die Summe seiner Eigenwerte a_i, weilAf¨ur Eigenzust¨ande|a_iidiagonal ist, und manAauch schreiben kann, als:

A =X

i

ai|aiihai| (1.32)

• (C) Der Dichteoperator eines reinen Zustands % erf¨ullt:

– %=%^† (hermitesch )

– % ist positiv, d.h. hϕ|%|ϕi ≥0 ∀|ϕi ∈ H – Sp%= 1 (Norm)

– Sp%² = 1 (rein)

Bemerkung: %_ψ =|ψihψ| ist rein.

Beweis:

Man kann leicht nachweisen, dass die oberen vier Eigenschaften erf¨ullt sind:

Die Matrix (%_ψ)_n,n⁰ =hn|ψihψ|n⁰i ist hermitesch, weil:

(%^†_ψ)_{n n}⁰ =%^∗_n⁰_n =hn⁰|ψi^∗hψ|ni^∗ = (%_ψ)_{n n}⁰

Außerdem ist:

h|%ψ|ϕi=|hϕ|ψi|² ≥0 sowie:

Sp%_ψ =X

n

hn|ϕihψ|ni=X

n

c_nc^∗_n =hψ|ψi= 1 und:

Sp%²_ψ = Sp|ψi hψ|ψi

| {z }

=1

hψ|= Sp %ψ = 1

• (D) Gemische

Ein quantenmechanisches System liege mit der Wahrscheinlichkeit ˜p_i in verschiede- nen (reinen) nicht interferenzf¨ahigen Zust¨anden|ψ_ii vor.

In einem solchen Gemisch lautet der Mittelwert eines Operators A:

< A >:=

I

X

i=1

˜

p_i hψ_i|A|ψ_ii (1.33)

Er setzt sich also zusammen aus dem statistischen Mittelwert und dem quantenme- chanischen Erwartungswert von A im Zustand ψ_ii.

Als Wahrscheinlichkeit muss ˜p_i die folgenden Bedingungen erf¨ullen:

– 0≤p˜_i ≤1 –

I

P

i=1

˜ p_i = 1

Beispiele hierf¨ur sind:

– M stoßende Teilchen in einer Box

– Der Strahl polarisierter Teilchen deren Position nicht kontrolliert wird.

– quantenmechanisches System in Kontakt mit W¨armebad Mit dem Dichteoperator

%:=

I

X

i=1

˜

p_i|ψihψ| (1.34)

lautet der Mittelwert:

< A >= Sp %A (1.35)

Durch Einf¨ugen der dyadischen Eins erh¨alt man:

< A >=X

n n⁰

hn|%|n⁰ihn⁰|A|ni

=X

n n⁰

hn⁰|A|ni

I

X

i=1

˜

p_ihn|ψ_ii

| {z }

cn(i)

hψ_i|n⁰

| {z }

c^(i)∗

n0

In der hinteren Summe liegt der Unterschied zum reinen Zustand (in der Matrix- Darstellung von %).

Definition:

Ein (statistischer) Dichteoperator % auf H erf¨ullt die folgenden Eigenschaften:

– %=%^† (hermitesch )

– % ist positiv, d.h. hϕ|%|ϕi ≥0∀|ϕi ∈ H – Sp%= 1 (Norm)

Der statisitsche Mittelwert eines beliebigen Operators A lautet dann im Zustand %:

< A >= Sp%A Bemerkungen:

– Zur Vereinfachung wird angenommen, dassH nicht unendlich-dimensional sei.

– % = P

i

˜

p_i|ψ_iihψ_i| ist der Dichteoperator und seine Aufenthaltswahrscheinlich- keit lautet:

hx|%|xi=

I

X

i=1

˜

p_i|hx|ψ_ii|²

• (E) Eigenschaften von %

– a) Eigenwerte & Eigenzust¨ande Die dyadische Zerlegung % =

ν

P

n=1

%n |nihn| existiert mit %|ni = pn|ni sowie hn|n⁰i = δ_nn⁰. Die Eigenwerte p_n geben die Wahrscheinlichkeit an, dass der Eigenzustand|ni im Gemisch vorliegt, somit muss f¨ur diese gelten:

0≤p_n≤1 &

ν

X

n=1

p_n = 1 Bemerkung:

% ist diagonal in den Eigenzust¨anden |ni (aber nicht notwendigerweise in den

|ψ_ii, weil hψ_i|ψ_ji 6= 0 m¨oglich ist)

Die |ni, wobei n f¨ur mehrere Quantenindizies stehen kann, sind Vielteilchen- Zust¨ande:

|ni=X

n

c⁽ⁿ⁾_n |ni ∈ H (1.36) spannen aber i.A. nichtHⁿ auf.

Beweis:

Die Tatsache, dass %hermitesch ist, liefert %=

ν

P

n=1

p_n|nihn| mit orthonormier- ter Eigenbasais von %. Weil laut Vorraussetzung hϕ|%|ϕi = P

n

p_n|hϕ|ni|² ≥ 0 ∀|ϕi ∈ H gilt, muss p_n ≥ 0 sein. Außerdem muss die Spur des Dichteope- rators gleich Eins sein und wegen Sp% = 1 =P

n

pn folgt somit pn ≤1 was zu zeigen war.

– b) reine Zust¨ande:

Geh¨ort % zu einem reinen Zustand (also Sp %² = 1), dann gelten folgende Aussagen:

∗ i)%² =% (d.h. % ist ein Projektor)

∗ ii)pn0 = 1 undpn= 0 sonst

∗ iii) % hat den Rang 1 Beweis:

Die Aussagen i)-iii) sind ¨aquivalent, aus%=|noihn0|folgt sofort, dass Sp%² = 1 gilt.

Ist nun anders herum Sp%² = 1, so hat %² die Eigenwerte p²_n ≤ p_n f¨ur p_n ≤ 1 Somit ist aber 1 =P

n

p²_n ≤ P

n

pn = 1, was nur mit ”=” erf¨ullt sein kann und damit ist gezeigt, dass pn0 = 1 &pn= 0 sonst gelten muss.

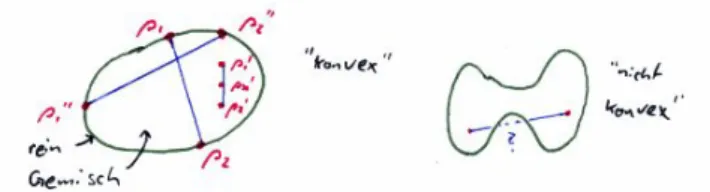
– c) Die Dichteoperatoren bilden eine konvexe Menge

Unter einer konvexen Menge kann man sich einen Kreis oder eine Ellipse vor- stellen. Man nennt die Menge konvex, weil jeder Punkt der Menge mit jedem anderen Punkt der Menge verbunden werden kann, so dass der Weg komplett in der Menge liegt. Auf dem Rand des Kreises liegen reine Zust¨ande innerhalb Gemische! Die mathematische Definition lautet:

Sind %₁ & %₂ zwei unterschiedliche Dichteoperatoren , so sind auch alle Kom- binationen %_x =x%₁+ (1−x)%₂ mit 0≤x≤1 (d.h. konvexe Kombinationen) Dichteoperatoren . % ist genau dann rein, wenn man den Zustand nicht als konvexe Kombination zerlegen kann.

1.2.3 (Un-)abh¨ angige Subsysteme

Abbildung 1.1: Subsystem 2 entspricht thermodynamischen W¨armebad

H sei ein f-dimensionaler Produkt-Hilbert-Raum: H = H₁ ⊗ H₂ zweier Subsysteme, wobei H r-dimensional und H₂ (f−r)-dimensional sei.

Spannen nun die |n₁i₁ den H₁ und die |n₂i₂ den H₂ auf, so bilden die Produktzust¨ande:

{|ni}=|n₁i+|n₂i2

mit n₁ =





 n11

... n_1r







&n₂ =





 n_2r+1

... n_2f





 eine Orthonormalbasis zu H.

• (A) Subsysteme & reduzierte Dichteoperatoren

% geh¨ore zu einem reinen Zustand in H, so gilt:

%=|ψihψ|=X

n

c_n|ni X

n⁰

c^∗_n⁰hn⁰|

=X

n n⁰

c_nc^∗_n⁰ |nihn⁰|

= X

n₁n⁰₁n₂n⁰₂

c_n1n2c^∗_n⁰

1n⁰₂ |n₁i₁|n₂i₂hn⁰₁|₁hn⁰₂|₂ =F mit P

n

|c_n|² = 1.

Wir wollen nun den Mittelwert eines OperatorsA1betrachten, der nur im Subsystem 1, d.h. auf den H₁, wirkt, d.h.:

A=A₁⊗I

2

Der OperatorA₁l¨asst die Zust¨ande inH₂unber¨uhrt und ver¨andert nur die im ersten Subsytem:

A1|ni= (A1 |n₁i1)⊗I

2 |n₂i2 =X

n⁰₁

α_{n n}⁰

1 |n⁰₁i1|n₂i2

Wir postulieren, dass der Mittelwert von A1 mit Hilfe des reduzierten Dichteopera- tors %₁ auf H₁ geschrieben werden kann, wobei:

%₁ = Sp₂%=X

n₂

hn₂|₂%|n₂i₂ (1.37)

Dies bedeutet, dass man ¨uber das Subsystem 2 aufintegriert bzw. absummiert.

Setzt man nun % aus F ein, so erh¨alt man:

%₁ = X

n₁n⁰₁

|n₁i₁hn⁰₁|₁ X

n₂

c_n

1n₂c^∗

n⁰₁n2 (1.38)

Beweis:

Zun¨achst soll bewiesen werden, dass %₁ ein Dichteoperator ist, dazu muss man die

Eigenschaften die ein Dichteoperator erf¨ullen muss ¨uberpr¨ufen:

%=%^† geht aus der Definition hervor.

Sp₁%₁ =X

n₁

hn₁|%₁|n₁i= X

n₁n₂

hn|%|ni= Sp%= 1 Bleibt also noch zu ¨uberpr¨ufen, ob %₁ positiv ist.

Dazu betrachten wir einen Zustand ϕi ∈ H₁ mit ϕi=P

n₁

d_n

1 |n₁i₁. Es folgt:

hϕ|₁%₁|ϕi₁ =X

n n⁰₁

d^∗_n⁰

1

d_n

1 c_nc^∗_n⁰

=X

n₂

A_n2

2 ≥0 mit A_n2 =X

n₁

d_n1 c_n1n2

Letzendlich gilt noch zu zeigen, wie man mit diesem reduzierten Dichteoperator den Erwartungswert von A₁ berechnet, dazu verwendet man wieder den ”Trick” eine dyadische Eins einzuschieben zwischen % und A₁:

< A₁ >= Sp (% A₁)=^∗ X

n₁n₂n⁰₁n⁰₂

hn₁|₁ hn₂|₂%|n⁰₁i |n⁰₂i

| {z }

P

n2

=hn₂|2%|n₂i |n⁰₁i=%1|n⁰₁i

hn⁰₁|A₁|n₁i hn⁰₂|n₂i

| {z }

=δn0 2n2

= X

n₁n⁰₁

hn₁|%₁|n⁰₁i hn⁰₁|A₁|n₁i=X

n₁

hn₁|%₁A₁|n₁i

= Sp₁ %1A1

wobei schon in * verwendet wurde, dass A₁ nur aufH₁ wirkt.

Damit ist gezeigt, dass man den Mittelwert des Operators A₁ wie folgt berechnet:

< A₁ >= Sp₁ %₁A₁ (1.39) Bemerkung:

Da%₁ undA₁nur auf den Zustand ausH₁ (d.h. Subsystem 1) wirken, kann Sp₁ %₁A₁ bestimmt werden, ohne dass man etwas ¨uber das Subsystem 2 weiß. Allerdings ge- hen dadurch Informationen verloren, so kann man aus%₁ nicht mehr den kompletten

% finden.

• (B) Unabh¨angigkeit & Gemische Definition:

Zwei Subsysteme eines quantenmechanischen Systems heißenunabh¨angig, wenn%=

%₁ ⊗ %₂ gilt (d.h. wenn der Dichteoperator des gesamten Systems sich aus dem Tensorprodukt der reduzierten Dichteoperators der beiden Subsysteme zusammen setzt.)

Das bedeutet f¨ur die Matrixdarstellung von %:

hn|%|n⁰i=hn₁|1 hn₂|2 %1⊗%2 |n⁰₁i1 |n⁰₂i2

=hn₁|1%1|n⁰₁i1 ⊗ hn₂|2%2|n⁰₂i2 (1.40)

Satz:

Geh¨ort der reduzierte Dichteoperator %₁ zu einem reinen Zustand, dann muss das Subsy- stem 1 vom Rest (hier Subsystem 2) unabh¨angig sein.

Beweis:

Zu zeigen ist die Behauptung

Sp₁ %²₁ = 1 ⇒ %=%₁⊗%₂

Ein beliebiger Dichteoperator auf H lautet in der Eigenbasis (mit den Eigenwerte p_n):

%=X

n

p_n |nihn|

wobei|ni=P

n

c⁽ⁿ⁾n |nidie Orthonormalbasis vonH ist. Somit kann%mit|ni=|n₁i₂ |n₂i₂

% geschrieben werden als:

%= X

n n n⁰

p_n c⁽ⁿ⁾

n⁰

^∗ c⁽ⁿ⁾_n

|nihn⁰|

Geht man damit in die Definition des reduzierten Dichteoperators :

%₁ = Sp₂%=X

n₂

hn₂|₂ %|n₂i₂ so erh¨alt man f¨ur%₁:

%₁ = X

n n₁n⁰₁

p_n |n₁i₁ hn⁰₁|₁ X

n₂

c⁽ⁿ⁾

n⁰₁n₂

∗

c⁽ⁿ⁾_n

1n₂

Da %₁ rein sein soll, muss nat¨urlich auch gelten: %₁ =|ψi₁hψ|₁.

Man kommt nun im Beweis weiter voran, wenn man die Orthonormalbasis inH so w¨ahlt, dass ψi1 =|n⁽⁰⁾₁ i1 ist, dann m¨ussen n¨amlich alle anderen Summanden verschwinden:

%₁ =|n⁰₁i₁hn⁰₁|₁ 0 =X

n n₂

p_n c⁽ⁿ⁾

n⁰₁n₂

∗

c⁽ⁿ⁾_n

1n₂ f¨ur n₁ 6=n⁽⁰⁾₁ 6=n⁰₁

Bei der speziellen Wahl von n₁ =n⁰₁ 6=n⁰₁ sieht man:

X

n n₂

P_n|c⁽ⁿ⁾_n

1n₂|² = 0

was bedeutet, dass c_n1n2 = 0 f¨ur alle n₂ &n₁ 6=n⁰₁. Damit erh¨alt der Dichteoperator die folgende Darstellung:

%=X

n

X

n₂n⁰₂

p_n c⁽ⁿ⁾

n⁰₁n⁰₂

∗

·c⁽ⁿ⁾_n0

1n₂ |n⁰₁i₁ |n₂i₂ hn⁰₁|₁hn⁰₂|₂

=: |n⁰₁i1hn⁰₁|1

| {z } reiner Zustand auf ^H1

⊗%2 =:%1⊗%2

Fazit:

Reduzierte Dichteoperatoren %₁ eines Subsystems sind fast immer Gemische, vor allem wenn sie in Kontakt mit der ”Umgebung” sind. Beim Licht, macht diese Tatsache gerade den Unterschied zwischen einer Lampe und einem Laser aus, w¨ahrend aus einer Lampe nur gemischte Zust¨ande emittiert werden, approximiert ein Laser in hohem Grade einen reinen Zustand.

Fast immer gibt es Korrelationen zwischen den Subsystemen 1 und 2 (Wechselwirkungen).

Gemische liegen auch dann vor, wenn das Subsystem 2 unkontrolliert ist und deshalb viele/alle seiner Zust¨ande annimmt. (Ein Beispiel hierf¨ur ist die ¨Ubungsaufgabe 9) Bemerkung:

F¨ur den Operator A₁ k¨onnen Korrelationen definiert werden:

K_ij =<∆A_i∆A_j >= Sp (∆A_i∆A_j%) (1.41) mit ∆A_i =A_i−< A_i >

Diese Korellationen erf¨ullen K_ij = 0 wenn A_i auf H₁ und A_j auf H₂ wirken und die Subsysteme 1 & 2 unabh¨angig sind.

Beweis:

K_ij = Sp (%₁⊗%₂·∆A_i∆A_j)

= Sp₁ (%₁∆A_i)·Sp₂ (%₂∆A_j) = 0 Auf Grund der Definition von ∆A_i

F¨ur nicht kommutierende OperatorenA_i&A_j istK_ij 6=K_jim¨oglich. (subtiler Unterschied der Quantenmechanik ) wiederum gilt aber:

X

ij

α^∗_i K˜_ijα_j =X

ij

(Sp (%∆A^∗_i∆A_j))α^∗_iα_j ≥0 (1.42)

= Sp (%|X|² (1.43)

mit X =X

i

α_i∆A_i

1.2.4 Von-Neumann-Gleichung

Die Zeitentwicklung eines reinen Dichteoperators%=|ψihψ|folgt aus derSchr¨odinger- Gleichung

∂_thψ(t)|= i

~hψ(t)|H(t)

i~∂_t%(t) =i~∂_t|ψ(t)ihψ(t)|

=∗ H(t)%(t)−%(t)H(t)

= [H,%]

In * wurde die Produktregel verwendet.

Werden im Gemisch %=P

i

˜

p_i |ψihψ_i| die ˜p_i als konstant angenommen, so gilt dort eben- falls:

∂_t%(t) =−i

~[H(t),%(t)] (1.44)

Dies ist die von-Neumann-Gleichung.

Bemerkung:

ImHeisenberg-Bild gilt d

dtA_H(t) = ⁱ

~[H,A_H] mit umgekehrten Vorzeichen. Dies ist eine Andeutung darauf, dass % kein geq¨ohnlicher (Heisenberg) Operator ist. Eigentlich ist der Dichteoperator eine Abbildung, die allen Operatoren ihren Mittelwert zuordnet, und davon abh¨angt in welchem quantenmechanischen Mikrozusatnd das System ist.

Bemerkung:

• Wenn ρ = ρ(H) ⇒ ∂_tρ = 0 weil eine Funktion des Hamiltonoperators mit diesem kommutiert.

1.3 Klassische Statistik

1.3.1 Der Phasenraum

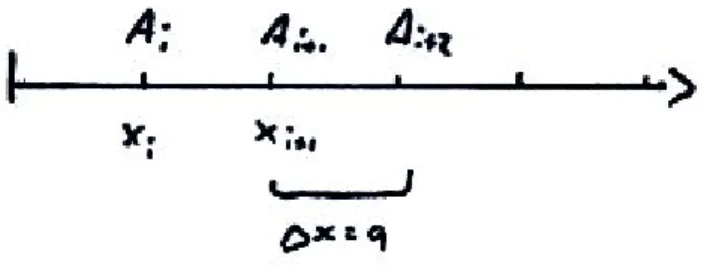
Dem Makrozustand eine N-Teilchen-Systems wird eine Wahrscheinlichkeitsdichte (Pha- senraumverteilungsfunktion)

ρ(r₁, ..., r_N, p

1, ...,p

N, t) = ρ({r}),{p}, t) = ρ(Γ) (1.45) im 6N-dimensionalen Phasenraum zugeordnet, so dass

ρ(Γ_N) dΓ_n mit

dΓ_N = 1 N! · 1

h^3N ·

N

Y

i=1

d³r_i d³p_i

(dem normierten Phasenraumvolumenelement) die Wahrscheinlichkeit ist, dass das Sy- stem den Mikrozustand mit

({r},{p})∈[({r},{p},{r+ dr},{p+ dp})]

annimmt. Die Normierung _N!¹ · _h3N¹ folgt aus der Quantenstatistik.

Der Mittelwert einer beliebigen Funktion A(Γ_N) im Phasenraum lautet:

hAi= Z

dΓ_N ρ(Γ_N)A(Γ_N) (1.46)

Liegt der Makrozustand genau in einem Mikrozustand vor, d.h. sind alle Orte und Impulse bekannt, lautet ρ:

ρmicro =h^3NN!

N

Y

i=1

δ(r_i−r_i(t))δ(p_i−p_i(t)) (1.47)

wobei die r_i(t) und p

i(t) der Trajektorie der Teilchen entspricht. In diesem Fall ist der Mittelwert einer solchen beliebigen Funktion im Phasenraum:

hAi=A({r(t)},{p(t)}) (1.48)

Bemerkungen:

• Da ρ eine Wahrscheinlichkeitsdichte ist, gilt die Diskussion von §1.1 (z.B. ρ erf¨ullt also ρ≥0 und Normierung auf 1)

1.3.2 Liouville-Theorem und Liouville-Gleichung

Die Bewegung der Teilchen folgt aus den Hamilton-Gleichungen

˙

r_i = ∂H

∂pi

und p˙

i =−∂H

∂r_i Die Zeitentwicklung eines Makrozustandes (ρ dΓ_N) besteht aus

• a) ... der Zeitabh¨angigkeit des Phasenraumvolumenelementes

• b) ... der Zeitabh¨angigkeit der Wahrscheinlichkeitsdichteρ

weil die Wahrscheinlichkeit von beiden Faktoren abh¨angt. Das Liouville-Theorem sagt nun aus, dass das Phasenraumvolumenelementes zeitlich konstant ist unter den Hamiltonschen Bewegungsgleichungen.

dΓ_N(t) =const. (1.49)

Um dies zu beweisen, schauen wir uns die Jacobi-Determinante der Variablentransforma- tion an:

{r(t0)},{p(t0)} ^H.Gl.→ {r(t)},{p(t)}

Hier erhalten wir also aus den Anfangswerten die L¨osung der hamiltonschen Bewegungs- gleichungen. Die Behauptung ist nun:

J = ∂({r(t)},{p(t)})

∂({r(t₀)},{p(t₀)}) = 1 Den Beweis hierzu f¨uhren wir im Eindimensionalen:

d

dtJ(t) = d

dsJ(t+s)|_s=0 = d ds

∂(r(t+s), p(t+s))

∂(r₀, p₀) |_s=0 = d ds

∂(r(t+s), p(t+s))

∂(r₀, p₀) · (∂r(t), p(t))

∂(r₀, t₀)

und mit den Gleichungen

r(t) =r₀+ ∂H

∂p |_r0,p0 +O(t²) p(t) =p₀− ∂H

∂q |_r0,p0 +O(t²) folgt:

d

dtJ(t) = d

dt det 1 + _{∂r ∂p}^∂2H|_r0,p0 ·t ^∂_∂p^2H2|_r0,p0 ·t

∂²H

∂r² |r0,p0 ·t _{∂p ∂r}^∂2H|r0,p0 ·t

!

= ∂²H

∂r ∂p|_r0,p0− ∂²H

∂p ∂r|_r0,p0 = 0 Daraus folgt die Aussage J(t) = 1, was zu beweisen war.

Bemerkungen:

• Der Grund, dass die statistische Mechanik im Phasenraum nur im Phasenraum arbeitet ist die Tatsache, dass wir nur ρ(Γ_N, t) ber¨ucksichtigen m¨ussen.

Die Liouville-Gleichung:

Die Wahrscheinlichkeitsdichte erf¨ullt mit der Poisson-Klammer:

∂

∂tρ={H, ρ}=

N

X

i=1

∂H

∂r_i · ∂H

∂pi

− ∂H

∂pi

· ∂H

∂r_i (1.50)

Beweis:

Da die Volumenelemente dΓ_n(t) im Phasenraum entlang einer Trajektorie konstant sind, nicht enden und sich nicht schneiden, folgt aus der Forderung, dass Wahrscheinlichkeit W =ρ dΓ_N = konst. entlang einer Trajektorie sein soll, die Erhaltung vonρ:

0 = ρ({r(t+ dt)},{p(t+ dt)}, t+ dt)−ρ({r(t)},{p(t)}, t) =δ%

= ∂ρ

∂t +

N

X

i=1

∂ρ

∂r_ir˙_i+ ∂ρ

∂pi

˙ pi

!

dt (1.51)

=∗ ∂ρ

∂t +

N

X

i=1

∂ρ

∂r_i ·∂H

∂pi

− ∂ρ

∂pi

· ∂H

∂qi

! dt

In * wurden die Hamiltonschen Bewegungsgleichungen eingesetzt. Bemerkung:

• Die Zeitabh¨angigkeit eines MittelwerteshAi hat zwei Interpretationen.

hAi(t) = Z

dΓ_N(t₀)ρ(Γ_N(t₀), t₀)A({r(t)},{p(t)}) ...eine Trajektorie mit den Startwerten {r(t₀)},{p(t₀)}, oder

hAi(t) = Z

dΓ_N(t)ρ

r₀({r(t)},{p(t)}), p

0({r(t)},{p(t)})

A({r(t)},{p(t)}) ... in Abh¨angigkeit von{r(t)},{p(t)}aber mit r¨uckw¨arts laufender Trajektorie, wel- che allerdings die Anfangsbedingungen erf¨ullt

• Wenn ρ=ρ(H, t), dann gilt _∂t^∂ρ= 0, wegen:

{ρ(H, t), H}= 0

1.4 Wichtige Gesamtheiten (Ensemble) und einf¨ uhren- de Beispiele

1.4.1 Das Beispiel paramagnetischer Salze

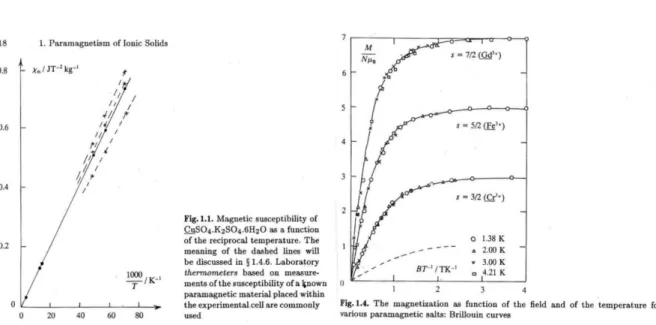
Hierbei handelt es sich um Kristalle mit nichtwechselwirkenden lokalisierten magnetischen Momenten M_i. In externen magnetischen Feldern richten sich diese aus und weisen eine Magnetisierung M auf. Beobachtungen sind:

• Die magnetische Suszeptibilit¨at ist definiert durch χ_m = _V¹ · ^∂M_∂B = _k^Mc2

BT mit der Curiekonstanten M_c². Diese Formel wurde aus experimentellen Befunden abgeleitet.

• Die Curie-Konstante ist positiv und l¨asst sich schreiben als 0< M_c²

k_B = N V · µ²_B

k_B ·konst.

mit µ_B als bohrschem Magneton und ^N_V als Dichte der magnetischen Momenten.

• Die Magnetisierung ist nicht von zwei Variablen unabh¨angig, da gilt:

M(T,B) = M B

T

Abbildung 1.2: Magnetisierungskurven

Unsere zentrale Annahme ist: Die magnetischen Momente wechselwirken nicht unterein- ander. Deshalb nehmen wir als Beispiel f¨ur folgende ¨Uberlegungen.

1.4.2 Der kanonische Dichteoperator

Das folgende System sei im thermodynamischen Gleichgewicht.

Abbildung 1.3: System aus zwei Subsystemen Wir betrachten die erhaltene Gesamtenergie. Sie lautet:

E =E1 +E2+UW W

Die Energien in den Subsystemen kommt von den systeminternen Wechselwirkungen. Die Wechselwirkung der beiden Subsysteme funktioniert nat¨urlich nur ¨uber die Grenzschicht.

Daraus gilt f¨ur das Volumen:

U_{W W} ∝V²³

da die Fl¨ache nur quadratisch skaliert, w¨ahrend das Volumen mit der dritten Potenz anw¨achst. Es gilt also im Grenzfall:

E →E₁+E₂ f¨ur V → ∞

wie bei zwei unabh¨angigen Subsystemen, welche eine Wahrscheinlichkeitsdichte ρ=ρ1⊗ρ2

besitzen. Die Energie als einzige Erhaltungsgr¨oße legt die Forderung nahe, dass:

ρ(E) = ρ₁(E₁)⊗ρ₂(E₂)

Unter Annahme identischer Funktionen ρ_i, da die Unterteilung ja k¨unstlich war, folgt:

ρ(E) = 1

Z ·e^−βE (1.52)

Dies ist eine eindeutige L¨osung mit der Normierung Z(β) = Sp e^−βE

(1.53) und der unbestimmte Parameter kann (klassisch) aus dem Mittelwert hEibestimmt wer- den, also

hEi= 1

Z SpE·e^−βE oder hEi= Z

dΓ_N ρ(Γ_N)E

Annahme: Auch die Verteilung auf mikroskopische Energieniveaus sei durch diese Vertei- lungsfunktion charakterisiert. Mit dem Hamiltonoperator H und der Orthonormalbasis {|ni} des Hilbertraums haben wir:

ρ(β) = 1

Z(β)e^−βH

Z(β) = Spe^−βH (1.54)

In Matrix-Darstellung sieht das folgendermaßen aus:

Z(β) = X

n

hn|e^−βH|ni