7. Neuronale Netze

7. Neuronale Netze

Einf¨ uhrung (1)

Ein k¨unstliches neuronales Netz ist vom Konzept her eine Realisierung von miteinander verschalteten Grundbausteinen, sogenannter Neuro- nen, welche in rudiment¨arer Form die Vorg¨ange im biologischen Vor- bild, unserem Gehirn, nachahmen. Wichtige Eigenschaften sind:

• Lernf¨ahigkeit,

• Parallelit¨at,

• Verteilte Wissensrepr¨asentation,

• Hohe Fehlertoleranz,

• Assoziative Speicherung,

• Robustheit gegen St¨orungen oder verrauschten Daten,

2

Einf¨ uhrung (2)

Der Preis f¨ur diese Eigenschaften ist:

• Wissenserwerb ist nur durch “Lernen” m¨oglich.

• Logisches (sequenzielles) Schließen ist schwer.

• Sie sind oft langsam und nicht immer erfolgreich beim Lernen.

Aus diesem Grunde werden Neuronale Netze nur dort angewandt, wo gen¨ugend Zeit f¨ur ein Lernen zur Verf¨ugung steht. Sie stehen in Kon- kurrenz z.B. zu Vektorraum-Modellen oder probabilistischen Modellen.

Es gibt viele fertige Softwarepakete f¨ur Neuronale Netze, siehe z.B.

Liste unter http://de.wikipedia.org/wiki/K¨unstliches_neuronales_Netz

Einf¨ uhrung (3)

Ein Neuronales Netz besteht aus verbundenen Neuronen

(ca. 10¹⁰ − 10¹¹ Neuro- nen bei einem Menschen mit ca. 10¹⁴ − 10¹⁵ Verbindungen).

Abbildung aus Wikipedia: https:// de.wikipedia.org/wiki/Neuronales Netz

4

Einf¨ uhrung (4)

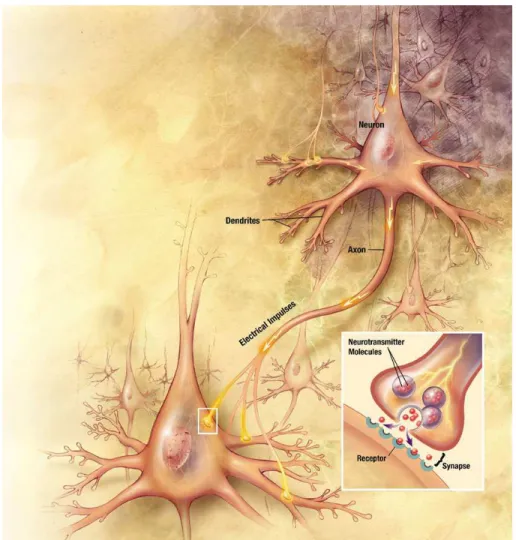
Ein Neuron hat

• Dendriten, die die Eingaben einsammeln

• Soma, der Zellk¨orper

• Axon, welches die Ausgabe der Zelle weiterleitet, sich verzweigt und mit den Dendriten nachfolgender Neuronen ¨uber Synapsen in Kontakt tritt.

• Synapsen sch¨utten Neurotransmitter aus, die anregend oder d¨amp- fend wirken.

Einf¨ uhrung (5)

Ein Modell eines Neurons:

X1 ω_1j Übertragungs- funktion

Aktivierungs- funktion

Ausgabe- funktion Eingabe

Gewichte

Schwellwert

Ausgabe

Xi ω_ij

Xn ω_nj

f_prop net f_act a f_out o

j j j

Die Ausgabe f¨uhrt zur Aussch¨uttung von Neurotransmittern und damit zu einer Eingabe der nachfolgenden Zellen bzw. Neuronen.

In den Aktivit¨aten der Neuronen ist die Information codiert.

6

Einf¨ uhrung (6)

Vereinfacht: Ein Neuron i mit n Eing¨angen (Dendriten) bekommt einen Gesamtinput von net_i und erh¨alt damit einem Aktivit¨atswert a_i.

Daraus folgt ein Ausgangswert o_i (Axon), der ¨uber eine synaptische Koppelung w_i,j an das Neuron j koppelt.

ai aj

net net

o o

i

i

j w i,j j

Neuronale Netze waren f¨ur l¨angere Zeit auf Grund der “Lernprobleme”

aus der Mode gekommen. Seit ca. 2005 erleben neuronale Netzwer- ke eine Wiedergeburt, da sie bei herausfordernden Anwendungen oft bessere Ergebnisse als konkurrierende Verfahren liefern.

Einf¨ uhrung (7)

Eine andere Sichtweise auf Neuronale Netze besteht darin, dass es sich schlicht und einfach um eine Darstellung eines Rechengraphen handelt, bei dem sich auf bestimmte Operationen beschr¨ankt wurde, die anschließend nicht explizit notiert wurden.

Zwei Beispiele von Rechengraphen

x

o

y z

a b

σ

dot +

x y

z

x

8

Einf¨ uhrung (8)

1. “Klassische” k¨unstliche Neuronale Netze

• Grundlage sind biologische Neuronen, jedoch in einer starken Vereinfachung, so dass sie mathematisch einfach und schnell zu behandeln sind.

• Heute werden sogenannte tiefe Netze (deep neural networks) verwendet, bei denen Neuronen ¨uber viele Schichten verbunden sind (siehe z.B. www.deeplearning.net/).

• Sie werden z.B. von Google, Apple, Facebook, NSA, BND und vielen anderen verwendet z.B. zur Bild- und Spracherkennung, in der Robotik, f¨ur Optimierungsprobleme usw.

• Fast t¨aglich gibt es neue Meldungen ¨uber neue Anwendungen.

Einf¨ uhrung (9)

Anwendungsgebiete nach Wikipedia (Stand 2016):

• Regelung und Analyse von komplexen Prozessen

• Fr¨uhwarnsysteme

• Optimierung

• Zeitreihenanalyse (Wetter, Aktien etc.)

• Sprachgenerierung

• Bildverarbeitung und Mustererkennung

* Schrifterkennung (OCR), Spracherkennung, Data-Mining

• Informatik: Bei Robotik, virtuellen Agenten und KI-Modulen in Spielen und Simulationen.

• Medizinische Diagnostik, Epidemiologie und Biometrie

• Klangsynthese

• Strukturgleichungsmodell zum Modellieren von sozialen oder be- triebswirtschaftlichen Zusammenh¨angen

10

Einf¨ uhrung (10)

Weitere aktuelle Anwendungsbeispiele (2016)

• Mit zwei tiefen Netzen, eins f¨ur die Vorhersage guter Z¨uge und eins f¨ur den Wert einer Stellung, ist es im M¨arz 2016 gelungen, einen Go-Meister zu schlagen. Hardware: 1202 CPUs mit 176 GPUs.

• Facebook sagt, das neue System Deep Text versteht Texte ge- nauso gut wie Menschen.

• Google Photo oder die Translater-App, auf Clustern trainiert, lau- fen jetzt auf dem Smartphone.

• Immer mehr Firmen entwickeln Empathiemodule.

• Google hat gerade f¨ur Neuronale Netze eine Tensor Processing Unit (TPU) entwickelt.

• In der MKL (Mathematical Kernel Library) von Intel gibt es jetzt ein Modul DNN (Deep Neural Network).

Einf¨ uhrung (11)

2. Neuronale Netze, nahe an der Biologie

Gr¨oßtes Beispiel in der EU: Das Human Brain Project https://www.humanbrainproject.eu/de

• Gestartet in 2013, F¨ordersumme 1,2 Milliarden Euro

• 6 Segmente: Neuroinformatik, Medizinische Informatik, Gehirn- simulation, Supercomputing, Neuronales Rechnen und Neuro- robotik.

• Beispiel BrainScaleS-System, Heidelberg. 20 Silizium-Wafer mit je knapp 200.000 Neuronen, ca. 58 Millionen Synapsen.

12

Einf¨ uhrung (12)

• Beispiel SpiNNaker-Projekt, Manchester. 1.036.800 Arm9-Kerne Jeder Kern simuliert Neuronen und 6 Synapsen.

http://apt.cs.manchester.ac.uk/projects/SpiNNaker/

In Betriebnahme 11.2018. Par- allele Kommunikationsarchitektur, dem Gehirns nachgebildet. Der Computer verteilt Millionen kleiner Informationspakete gleichzeitig.

Unabh¨angig von diesem Projekt gibt es jede Menge “kleine” Arbeiten, z.B. unsere hier.

Im folgenden werden diese Projekte nicht weiter betrachtet.

Mathematisches Modell (1)

Mathematisches Modell von neuronalen Netzen

Die klassischen k¨unstlichen Neuronalen Netze vereinfachen das biolo- gische Vorbild so stark, dass

• viele biologische Eigenschaften verloren gehen,

• aber die Grundidee erhalten bleibt und

• eine “schnelle” Berechnung m¨oglich ist.

Mathematisch heißt das, der Weg von der Eingabe eines Neurons zur Eingabe des damit verbundenen Neurons wird durch sehr einfache Funktionen beschrieben.

14

Mathematisches Modell (2)

Ein k¨unstliches neuronales Netz besteht aus folgenden Komponenten 1. Neuronen mit einem Aktivierungszustand a_i(t) zum Zeitpunkt t. 2. Eine Aktivierungsfunktion f_act, die angibt, wie sich die Aktivierung

in Abh¨angigkeit der alten Aktivierung a_i(t), des Inputs net_i und eines Schwellwerts Θ_i mit der Zeit ¨andert.

a_i(t + 1) = f_act(a_i(t), net_i(t),Θ_i).

3. Eine Ausgabefunktion f_out, die aus der Aktivierung des Neurons den Output berechnet

o_i = f_out(a_i).

Mathematisches Modell (3)

4. Ein Verbindungsnetzwerk mit den Koppelungen w_i,j (Gewichtsma- trix).

5. Eine Propagierungsfunktion, die angibt, wie sich die Netzeingabe aus den Ausgaben der anderen Neuronen berechnet, meist einfach

net_j(t) = ^X

i

o_i(t)w_i,j

6. Eine Lernregel, die angibt, wie aus einer vorgegebenen Eingabe eine gew¨unschte Ausgabe produziert wird. Dies erfolgt meist ¨uber eine Modifikation der St¨arke der Verbindungen als Ergebnis wie- derholter Pr¨asentation von Trainingsmustern.

Auf diese Weise werden die “Zust¨ande” ge¨andert, bis ein stabiler (und hoffentlich erw¨unschter) Endzustand eintritt, welcher in gewisser Wei- se das Ergebnis der Berechnungen eines neuronales Netzes darstellt.

16

Mathematisches Modell (4)

In vielen Anwendungen wird die Zeitabh¨angigkeit, z.B. bei der Ob- jekterkennung weggelassen und es werden ganz einfache Funktionen verwendet:

• Die Ausgabefunktion ist einfach

o_j = f_out(a_j) = a_j

• Propagierungsfunktion lautet

net_j = ^X

i

o_iw_i,j

• Die Ausgabe berechnet sich dann ¨uber

o_j = a_j = f_act(net_j,Θ_j)

wobei f¨ur f_act eine Stufenfunktion, der Tangens Hyperbolicus, die logistische Funktion oder zur Zeit besonders die ReLU-Funktion (rectified linear unit) popul¨ar sind.

Mathematisches Modell (5)

Stufenfunktion:

o_j = f_act(net_j,Θ_j) ==

( 1 falls net_j ≥ Θ_j 0 sonst

Tangens Hyperbolicus

o_i = tanh(c(net_i − Θ_i)). Logistische Funktion oder Sigmoidfunktion

o_i = 1/(1 + exp(−c(net_i − Θ_i)))

Die Konstante c beeinflusst die Steigung der Funktionen.

Mathematisches Modell (6)

-1 -0.5 0 0.5 1 1.5

-1 -0.5 0 0.5 1 1.5 2 2.5 3

output

input

Aktivierungsfunktionen Stufenfunktion Tangens Hyperbolicus Logistische Funktion

Hier wurde c = 5 und Θ = 1 verwendet. Meist wird aber c = 1 gesetzt.

19

Mathematisches Modell (7)

Die ReLU-Funktion, oder ‘leaky ReLU-Funktion ist einfach

f(x) =







x if x > 0 a otherwise

-0.2 0 0.2 0.4 0.6 0.8 1 1.2 1.4

-1.5 -1 -0.5 0 0.5 1 1.5

output

input

Aktivierungsfunktion Leaky ReLU

Hier wurde a = 0.02 und Θ = 0 verwendet. Die Funktion ist absolut

“unbiologisch”, aber sie funktioniert h¨aufig sehr gut, z.B. bei Netzen zur Objekterkennung, und ist extrem schnell zu berechnen!

Mathematisches Modell (8)

Beispiel: Ein nettes kleines bekanntes Netz mit wenigen Verbindungen und welches im Kopf nachzurechnen ist, ist das XOR-Netzwerk mit 4 Neuronen.

1.5 0.5

1

-2

1

1 1

n1 n2

n3 n4

Die Neuronen beinhalten die Schwellwerte, die Verbindun- gen sind mit den Gewichten beschriftet.

Als Aktivit¨atsfunktion bzw. f¨ur die Ausgabe wird eine Stufenfunktion gew¨ahlt

21

Mathematisches Modell (9)

Weiterhin wird die standardm¨aßige Propagierungsfunktion verwendet net_j = ^X

i

o_iw_i,j

also gilt

o_j =

( 1 falls ^P_i o_iw_i,j ≥ Θ_j

0 sonst .

Aus der folgenden Tabelle ist die Funktionsweise des Netzes ersicht- lich:

o₁ o₂ net₃ Θ₃ o₃ net₄ Θ₄ o₄

0 0 0 1.5 0 0 0.5 0

0 1 1 1.5 0 1 0.5 1

1 0 1 1.5 0 1 0.5 1

1 1 2 1.5 1 0 0.5 0

Mathematisches Modell (10)

Beschr¨ankt man sich auf ebenenweise verbundene feedforward-Netze, so wird f¨ur die XOR-Funktion ein weiterer verdeckter Knoten ben¨otigt.

0.5

0.5

1 1

-1 -1

n1 n2

n3

n5

n4 0.5

1 1

Eine kleine ¨Ubungsaufgabe: Wie sieht die zugeh¨orige Tabelle von Eingabe zur Ausgabe aus?

23

Mathematisches Modell (11)

Eingabeschicht: o_1,o₂

Aktivierungsfunktion: tanh(x) net₁ = o₁w₁₁ + o₂w₂₁ + Θ₁ net₂ = o₁w₁₂ + o₂w₂₂ + Θ₂ o^′₁ = tanh(net₁)

o^′₂ = tanh(net₂)

net_o = o^′₁w_1o + o^′₂w_2o + Θ_o

o_o = tanh(net_o) ^{n_1 n_2}

n_1

n_o

n_2 w_11

θ_1 θ_2

θ_ο

w_12 w_21 w_22 w_2o

w_1o

’ ’

Insgesamt ergibt sich die Funktion

o_o = tanh( ( tanh(o₁w₁₁ + o₂w₂₁ + Θ₁ ) w_1o +

( tanh(o₁w₁₂ + o₂w₂₂ + Θ₂ ) w_2o + Θ_o

Aufgabe des “Lernens”: Bestimmung der 9 Parameter w₁₁, w₁₂, w₂₁, w₂₂, w_1o, w_2o,Θ₁,Θ₂,Θ_o, so dass sich f¨ur alle m¨oglichen Werten o₁, o₂ die gew¨unschten o_o ergeben.

Darstellung von neuronalen Netzen (1)

Ein neuronales Netz ist ein Graph mit Kanten und Knoten. Neuronen bzw. Zellen sind aktive Knoten oder Berechnungseinheiten, die lokal auf Eingaben reagieren und Ausgaben produzieren, die ¨uber die Kanten weiter gegeben werden.

Eine andere Darstellung besteht aus Matrizen oder allgemeiner aus Feldern mit mehreren Indices oder Tensoren:

• Verbindungsmatrix w[Ebene][Ausgangsneuron][Eingangsneuron]

• Schwellwertmatrix Θ[Ebene][N euron]

• Eingangsmatrix net[[Ebene][N euron]

Rechnungen erfolgen durch Neuberechnung der Ausgabematrix o[Ebene][N euron].

Oft kommt bei ein weiterer Index f¨ur das Eingabemuster hinzu.

25

Darstellung von neuronalen Netzen (2)

Tensoren: Tensoren sind Gr¨oßen aus der linearen Algebra, um Objekte aus der linearen Algebra in ein einheitliches Schema einzuordnen.

Tensoren haben Indizes. Die Anzahl der Indizes gibt den Rang oder die Stufe des Tensors an.

• Tensoren nullter Stufe sind Skalare

• Tensoren erster Stufe sind Vektoren

• Tensoren zweiter Stufe sind Matrizen

Neuronale Netze werden durch Tensoren beschrieben, deshalb nennt Google seine Softwarebibliothek Tensorflow und seinen Spezialpro- zessor Tensorprozessor.

Arten von Verbindungsnetzwerken: Je nach Netztopologie und der Art der Verarbeitung der Aktivit¨atswerte werden verschiedene neuro- nale Netze unterschieden.

Darstellung von neuronalen Netzen (3)

Eine Einteilung nach R¨uckkopplung:

1. Netze ohne R¨uckkopplung (feedforward-Netze),

• Ebenenweise verbundene feedforward-Netze

• Allgemeine feedforward-Netze 2. Netze mit R¨uckkopplung,

• Netze mit direkter R¨uckkopplung (direct feedback, zur¨uck zu Eingabeknoten),

• Netze mit indirekter R¨uckkopplung (indirect feedback, zur¨uck zu Zwischenknoten),

• Netze mit R¨uckkopplung innerhalb einer Schicht (lateral feed- back),

• Vollst¨andig verbundene Netze (lateral feedback).

27

Darstellung von neuronalen Netzen (4)

2 Beispiel-Topologien und ihre Verbindungsmatrizen:

1 2

3 4 5

6 7

1 2

3 4 5

6 7

feedforward, ebenenweise verbunden

vollständig verbunden, ohne direkte

Rückkopplung

Darstellung von neuronalen Netzen (5)

Zwei zur Zeit h¨aufig angewendete Architekturen

• Feedforward Networks (FFN), meist in der Form sogenannter Mul- tilayer Perceptrons (MLP) oder in der Form von Convolution Neural Networks (CNN) (Faltungsnetze, ¨uberlappende Teilbereiche), z.B.

in der Bildverarbeitung.

• Rekurrent Neuronal Networks (RNN), also solche mit R¨uckw¨arts- verbindungen, z.B. in der Form von Long Short Term Memory Networks (LSTM) f¨ur handgeschriebene Texte oder in der Spra- cherkennung.

Diese Architekturen und deren Anwendung werden in den letzten Jah- ren fast ¨uberall diskutiert, z.B. seit ein paar Jahren auch in Zeitschrif- ten wie C’t

29

Darstellung von neuronalen Netzen (6)

Beispiel eines feedforward Netzes, ein multiplayer Perceptron f¨ur eine Klassifizierung:

o1

Eingabe

Ausgabe

om

ω₁₁

ω_1i

ω_1n

x1 xi

xn

Eingabe z.B. Pixel eines Bildes (Ge- sicht, Zahl, Tier ...

Ausgabe ein Neuron pro Name, pro Zahl, Art des Tiers ...

Darstellung von neuronalen Netzen (7)

Das Sch¨one an einem solchen Netz ist folgendes:

Wenn die Parameter, also die Gewichte w_i,j und die Schwellwerte Θ_i gut bestimmt wurden, gilt:

• kleine ¨Anderungen des Netzes (Verbindungen defekt)

• oder kleine Eingabe¨anderungen (Bild verrauscht)

→ _{kleine ¨}Anderung der Ausgabewerte

→ Bild wird h¨ochst wahrscheinlich trotzdem erkannt, da das gleiche Neuron den gr¨oßten Wert haben wird.

31

Lernen (1)

Wie werden gute Parameter bestimmt oder woher “weiß” ein Netz, welches Neuron bei welchem Bild aktiv sein soll?

M¨ogliche Arten des Lernens

1. Entwicklung neuer Verbindungen 2. L¨oschen existierender Verbindungen

3. Modifikation der St¨arke von Verbindungen 4. Modifikation der Schwellwerte der Neuronen

5. Modifikation der Aktivierungs-, Propagierungs- oder Ausgabefunk- tion

6. Entwicklung neuer Neuronen 7. L¨oschen von Neuronen

Lernen (2)

Lernverfahren

Meist wird die Modifikation der St¨arke von Verbindungen w_i,j verwen- det, da diese Verfahren am einfachsten sind und die Entwicklung bzw.

das L¨oschen von Verbindungen mit eingeschlossen werden kann.

Prinzipiell werden 3 Arten von Lernverfahren unterschieden:

1. ¨Uberwachtes Lernen, bei dem einem Netzwerk zu einem Input ein gew¨unschter Output gegeben wird, nach dem es sich einstellt.

2. Best¨arkendes Lernen, bei dem zu einem Input die Information, ob der Output richtig oder falsch ist, in das Netz zur¨uckgegeben wird.

3. Un¨uberwachtes Lernen, bei dem sich das Netz selbst organisiert.

Am h¨aufigsten ist das ¨uberwachte Lernen. Von den verschiedenen Lernmethoden wird hier nur das klassische Backpropagation-Verfahren vorgestellt.

33

Lernen (3)

Hebbsche Lernregel

Die einfachste Lernregel, die heute noch Grundlage der meisten Lern- regeln ist, wurde 1949 von Donald O.Hebb entwickelt.

Wenn Neuron j eine Eingabe von Neuron i erh¨alt und beide gleichzei- tig stark aktiviert sind, dann erh¨ohe das Gewicht w_ij, die St¨arke der Verbindung von i nach j.

∆w_ij = ηo_ia_j

Die Konstante η wird als Lernrate bezeichnet. Verallgemeinert lautet die Hebbsche Regel

∆w_ij = ηh(o_i, w_ij)g(a_j, t_j)

t_j ist die erwartete Aktivierung (teaching input), ein Parameter der Funktion g. Fast alle Lernregeln sind Spezialisierungen der Funktionen h und g.

Perzeptron (1)

Im folgenden werden wir uns aus Zeitgr¨unden nur eine Art von Netz mit einer Lernregel genauer ansehen, ein feedforward Netz in der Art des multiplayer Perzeptrons mit der Backpropagation-Lernregel.

Ursprung hat das Perzeptron aus der Analogie zum Auge, bei dem die Retina die Input-Neuronen beinhaltet, von der ¨uber eine Zwi- schenschicht eine Klassifikation der einzelnen Bilder in der Ausgabe- schicht erfolgt.

Dementsprechend werden solche Netze z.B. in der Steuerung auto- nomer Fahrzeuge eingesetzt.

Ausgabeneuron (Lenkung)

Eingabeneuronen (Straßenbild+entfernungen)

35

Perzeptron (2)

Aufbau:

• Es gibt eine Input-Schicht

• Es gibt keine, eine oder mehrere verborgene Schichten (hidden layer)

• Es gibt eine Ausgabe-Schicht

• Die Kanten verbinden die Schichten eine nach der anderen in der gleichen Richtung untereinander, d.h. die Informationen aller Kno- ten der Input-Schicht laufen in die selbe Richtung, nicht zur¨uck und nicht zwischen den Knoten einer Schicht.

In einigen F¨allen wird der Begriff Perzeptron enger als feedforward- Netz mit keiner oder einer verborgenen Schicht verwendet.

Backpropagation-Regel (1)

• Gegeben sind Eingabewerte, z.B. der MNIST-Datensatz^∗ mit 60000 Bilder der Gr¨oße 28x28 Pixel, auf denen handgeschriebene Ziffern abgebildet sind, ein Standard-Benchmark f¨ur Neuronale Netze.

• Das ergeben 784 Eingabeknoten und 10 Ausgabeknoten, f¨ur jede Ziffer einer.

• Ziel ist es, f¨ur ein gegebenes Bild p die Funktionen, die die Ausga- be o_p des Netzes berechnen, so zu bestimmen, dass z.B. nur der Knoten, der der dem Bild entsprechenden Ziffer zugeordnet ist, einen Wert 1 hat und alle anderen Ausgabeknoten einen Wert 0 haben, was dann die gew¨unschten Ausgabewerte t_p f¨ur dieses Bild w¨aren (es gibt auch andere Zuordnungen).

∗http://yann.lecun.com/exdb/mnist/

37

Backpropagation-Regel (2)

• Ein Maß f¨ur die Abweichung des berechneten von dem gew¨unsch- ten Ergebnis ist die Summe der quadratischen Abweichungen ¨uber alle Bilder p und alle Ausgabeneuronen j: das Fehlerfunktional

E =

P X p=1

E_p E_p = 1 2

n_out X

j

o_p,j − t_p,j²

• Die Funktionen, die die Ausgaben o_p,j berechnen, h¨angen von den Gewichten der Verbindungen zwischen den Knoten und den Schwellwerten der einzelnen Knoten ab.

• Backpropagation ist ein Gradientenabstiegsverfahren, bei dem die Gewichte und Schwellwerte so ge¨andert werden, dass das Fehlerfunktional (oder die Energiefunktion) minimiert wird.

Backpropagation-Regel (3)

Numerik bei mir: lineare Ausgleichsrechnung

Definition (Ausgleichsproblem)

Gegeben sind n Wertepaare (x_i, y_i), i = 1, . . . , n mit x_i 6= x_j f¨ur i 6=

j. Gesucht ist eine stetige Funktion f, die in einem gewissen Sinne bestm¨oglich die Wertepaare ann¨ahert, d.h. dass m¨oglichst genau gilt:

f(x_i) ≈ y_i f¨ur i = 1, . . . , n.

39

Backpropagation-Regel (4)

Numerik bei mir: lineare Ausgleichsrechnung

Statistik, 3. Semester: Methode der kleinsten Quadrate

Definition (Fehlerfunktional)

Gegeben sei eine Menge F von stetigen Funktionen sowie n Wertepaa- re (x_i, y_i), i = 1, . . . , n. Ein Element von f ∈ F heißt Ausgleichsfunktion von F zu den gegebenen Wertepaaren, falls das Fehlerfunktional

E(f) =

n X i=1

(f(x_i) − y_i)²

f¨ur f minimal wird, d.h. E(f) = min{E(g)|g ∈ F}. Die Menge F nennt man auch die Menge der Ansatzfunktionen.

Es werden also die Parameter der Funktion f(x) so bestimmt, so dass die Funktion m¨oglichst dicht an den Punkten liegt.

Backpropagation-Regel (4)

Ist die Funktion f(x_i) linear in den Parametern, also f(x) = ^Pp_k=1 a_kg_k(x), so l¨asst sich das Minimum des Fehlerfunktionals ¨uber die Nullstelle der Ableitungen von E(f) durch L¨osen einer linearen Gleichung f¨ur die Pa- rameter a_k bestimmen.

Jetzt:

• Jedem x-Wert entspricht einem Satz von Eingabewerten bzw. ein Eingabe-”Pattern” in_p,i mit i ≤ 1 ≤ n_in Werten.

• Jedem y-Wert entspricht einem Satz von Ausgabewerten bzw.

Ausgabe-”Pattern” t_p,j mit j ≤ 1 ≤ n_out Werten.

• Die Ausgleichsfunktion f(x) ist jetzt ein Satz von nicht-linearen Funktionen in einer Anzahl von Parameter, z.B. in den Gewichten des neuronalen Netzes: f_i,j(in_p,i, w_i,j) = o_p,j.

41

Backpropagation-Regel (5)

• Dann lautet das Fehlerfunktional, die Summe der quadratischen Abweichungen anstatt

E =

n X i=1

E_i E_i = (f(x_i) − y_i)² jetzt

E = ^X

p

E_p E_p = 1 2

n_out X

j

o_p,j − t_p,j²

• Gesucht in dem nicht-linearen Ausgleichsproblem: das Minimum von E als Funktion der nicht-linearen Parameter.

• Hinweis: H¨aufig werden auch andere Fehlerfunktion verwendet.

Das Minimum kann nicht exakt bestimmt werden, sondern es wird ge- sucht, in dem z.B. die Parameter entlang der negativen Steigung des Fehlerfunktionals ge¨andert wird ⇒ Backpropagation oder Gradienten- abstiegsverfahren.

Backpropagation-Regel (6)

0 1 2 3 4 5 6 7 8

0 2 4 6 8 10 12 14 16

error

w_i,j

Fehlerfunktion fuer ein Gewicht w_i,j

Die Aufgabe ist es ein m¨oglichst gutes Minimum zu finden.

Problem: Das funktioniert nur gut, wenn die Startwerte in der N¨ahe eines guten Minimums sind.

43

Backpropagation-Regel (7)

Vor der Ableitung des Algorithmus ist eine Vereinheitlichung der No- tation von Vorteil: Der Schwellwert-Wert eines Knotens wird interpre- tiert als eine Verbindung zu dem Knoten von einem Konten mit dem Ausgabewert 1 und einem Gewicht.

Mit w_n+1,j = −Θ_j und o_n+1 = 1 gilt

n X i=1

o_iw_i,j − Θ_j =

n+1 X i=1

o_iw_i,j ≡ net_j(t)

Backpropagation-Regel (8)

Der Backpropagation-Algorithmus ¨andert die Gewichte w_i,j von einem Knoten i zu einem Knoten j entlang des negativen Gradienten der Fehlerfunktion, bis diese (hoffentlich) minimal ist.

∆w_ij = −η ^X

p

∂E_p

∂w_ij.

Zur Berechnung der Ableitungen nochmal die Formal f¨ur das XOR- Problem mit 2 versteckten Kno- ten (Schwellwerte werden Bias- Konten und die Aktivierungsfunkti- on f_act(x) = tanh(x) wird allgemein geschrieben).

Eingabeschicht: o_1,o₂

net₁ = o₁w₁₁ + o₂w₂₁ + w₃₁ net₂ = o₁w₁₂ + o₂w₂₂ + w₂₃ o^′₁ = f_act(net₁)

o^′₂ = f_act(net₂)

net_o = o^′₁w_1o + o^′₂w_2o + w_3o o_o = f_act(net_o)

45

Backpropagation-Regel (8)

Zerlege die Ableitung des Fehlerfunktionals nach den Gewichten in einzelne Schritte:

Ableitung nach den Gewichten zur Ausgabeschicht: Der Fehler h¨angt ab o_o, das wiederum von net_o, das wiederum von w_io ab.

Ableitung nach den Gewichten zur verdeckten Schicht: Der Fehler h¨angt ab o_o, das wiederum von net_o, das wiederum von o₁, o₂, das wiederum von net₁, net₂ und das von w_i1

Verwende die Kettenregel, zuerst f¨ur den letzten Schritt:

∂E_p

∂w_ij = ∂E_p

∂net_pj

∂net_pj

∂w_ij .

Backpropagation-Regel (8)

Der erste Faktor wird als Fehlersignal bezeichnet δ_pj = − ∂E_p

∂net_pj und der zweite Faktor ist

∂net_pj

∂w_ij = ∂

∂w_ij

X k

o_pkw_kj = o_pi.

Die ¨Anderung der Gewichte berechnet sich dann durch

∆w_ij = η ^X

p

o_piδ_pj

Bei der Berechnung von δ_pj geht die konkrete Aktivierungsfunktion ein, also wie das Neuron j den Input in einen Output verwandelt.

δ_pj = − ∂E_p

∂net_pj = −∂E_p

∂o_pj

∂o_pj

∂net_pj = −∂E_p

∂o_pj

∂f_act(net_pj)

∂net_pj = −∂E_p

∂o_pjf_act^′ (net_pj).

47

Backpropagation-Regel (9)

F¨ur den ersten Faktor muss zwischen den Ebenen, in denen sich die Knoten befinden, unterschieden werden.

1. j ist Index eines Ausgabeneurons. Dann gilt

−∂E_p

∂o_pj = −1 2

∂

∂o_pj

n_out X

k

o_p,k − t_p,k² = (t_pj − o_oj). Der Gesamtfehler ist in diesem Fall

δ_pj = f_act^′ (net_pj) · (t_pj − o_oj)

2. j ist Index eines Neurons der verdeckten Ebenen. Die Fehlerfunk- tion h¨angt von den Output o_j indirekt ¨uber die Zwischenzellen k ab, denn der Output o_j geht in den Input net_pk von allen Knoten k eine Schicht “h¨oher” ein.

Backpropagation-Regel (10)

−∂E_p

∂o_pj = −^X

k

∂E_p

∂net_pk

∂net_pk

∂o_pj

= ^X

k



δ_pk ∂

∂o_pj

X i

o_piw_ik



 = ^X

k

δ_pkw_jk

Das bedeutet, dass man den Gesamtfehler des Neurons j f¨ur ein Muster p aus den gewichteten Fehlern δ_pk aller Nachfolgezellen k und der Gewichte der Verbindungen von j zu diesen k berechnen kann.

δ_pj = f_act^′ (net_pj) · ^X

k

δ_pkw_jk

Zusammengefasst

∆w_i,j = η ^X

p

o_p,if_act^′ (net_pj) ·







(t_pj − o_oj) falls j Ausgabeneuron

Pk δ_pkw_jk falls j verdecktes Neuron

49

Backpropagation-Regel (11)

Meist wird als Aktivierungsfunktion die logistische Funktion verwendet mit der Ableitung

d

dxf_log(x) = d dx

1

1 + e^−x = f_log(x) · (1 − f_log(x))

Damit ergibt sich eine vereinfachte Formel f¨ur den Backpropagation Algorithmus

∆_pw_ij = ηo_piδ_pj mit dem Fehlersignal

δ_pj =

( o_pj(1 − o_pj)(t_pj − o_pj) falls j Ausgabeneuron o_pj(1 − o_pj) ^P_k δ_pkw_jk falls j verdecktes Neuron

)

Backpropagation-Regel (12)

Beispiel: Netz mit 3 Ausgabeknoten n₁, n₂ und n₃

n7 n4

n1 n2 n3

W

W74 42

∆w_4j = ηo₄δ_j = ηo₄(t_j − o_j) ∗ f^′(net_j), j = 1,2,3

∆w₇₄ = ηo₇δ₄ = ηo₇(−

3 X j=1

δ_jw_4j)f^′(net₄)

51

Backpropagation-Regel (13)

Das Verfahren zusammengefasst

1. Berechne bei einem gegebenem Input den Output oder “Propa- gierung” ein Signales ¨uber die Schichten:

• Die Ausgaben der Neuronen i (oder die Werte der Inputneu- ron i) einer Schicht werden an die Eingaben der Knoten j der n¨achsten Schicht weitergeleitet ¨uber

net_j(t) =

n+1 X i=1

o_iw_i,j

• Die Knoten j berechnen die Ausgabe, die eventuell an die n¨achs- te Schicht weiter geleitet wird, ¨uber

o_j = f_act(net_j)

• Ist man an der Ausgabeschicht angekommen, ¨uberpr¨ufe, ob das Eingabesignal erkannt wird, also berechne den Fehler bzw. das Fehlerfunktional.

Backpropagation-Regel (14)

2. Ist der Fehler zu groß, f¨uhre eine R¨uckpropagierung durch.

• Berechne das Fehlersignal, von der Ausgabeschicht beginnend r¨uckw¨arts bis zur Eingabeschicht.

• Berechne die Korrektur der Gewichte gem¨aß

∆_pw_ij = ηo_piδ_pj

3. Beginne mit der Prozedur von vorne, bis der Fehler (hoffentlich) klein geworden ist, also die Eingaben gelernt wurden.

53

Backpropagation-Regel (15)

Das Beispiel vom Anfang:

o_o = tanh( ( tanh(o₁w₁₁ + o₂w₂₁ + Θ₁ ) w_1o + ( tanh(o₁w₁₂ + o₂w₂₂ + Θ₂ ) w_2o + Θ_o

• Ableitung der Aktivierungsfunktion: tanh^′ = (1 − tanh²)

• “Fehler” bei der Ausgabe: t_o − o_o

• Fehlersignal am Ausgabeknoten n_o: δ_o = (1 − o²_o)(t_o − o_o)

• Korrektur der Gewichte vom verdeckten Konten n_i zum Ausgabe- knoten n_o: ∆w_i,o = ηo_iδ_o

• “Fehler” beim verdeckten Knoten n_j: δ_ow_j,o

• Fehlersignal am verdeckten Knoten n_j: δ_j = (1 − o²_j)δ_ow_j,o

• Korrektur der Gewichte vom Eingangkonten n_i zum verdeckten Knoten n_j: ∆w_i,j = ηo_iδ_j

Backpropagation-Regel (16)

Probleme:

a) Bei zu kleinen Lernraten geht der Algorithmus nicht ¨uber das lokale Mi- nimum hinaus.

b) Kleine Gradienten wie bei Plateaus sorgen f¨ur eine erhebliche Mehrzahl an notwendigen Iterationsschritten.

c) Ungeeignete Wahl einer Lernrate bei zu großen Gradienten bewirkt Os- zillation des Lernprozesses

d) oder unter Umst¨anden ein ¨Uber- springen des globalen Minimums hin zu einem lokalen.

55

Backpropagation-Regel (17)

Noch zu beachten:

• Werden f¨ur jede Eingabe einzeln neue Gewichte berechnet, spricht man von online-learning.

• Werden erst die Fehler f¨ur alle Eingaben aufsummeriert (so wie in der Herleitung), heißt das batch-learning.

• Meist werden die Fehler f¨ur Bl¨ocke von Eingaben und damit Kor- rekturen f¨ur die Gewichte berechnet.

• F¨ur die Initialisierung der Gewichte gibt es verschiedene Methoden, am einfachsten sind gleichverteilte oder Gauß-verteilte Zufallszah- len.

• Die Lernrate sollte kleiner werden mit kleiner werdendem Fehler.

• ... und vieles mehr.

CNN (1)

Neben den Multilayer Perceptrons sind heute die meist verwendeten Netze Faltungsnetze bzw. Convolution Neural Networks (CNN).

• Die meisten Daten liegen in “Gittern” vor (Bilder bei der Bilderken- nung, 2 Dimensionen, Pixel, oder T¨one bei der Spracherkennung, diskrete Zeitabst¨ande, Frequenzen, 1 Dimension)

• Die Daten sind “translationsinvariant”, d.h. eine Katze unten rechts im Bild muss genauso erkannt werden wie oben links im Bild.

• Ein Gesamtbild setzt sich aus lauter benachbarten Einzelteilen zu- sammen, mehrere “benachbarte” T¨one werden zu einem Wort, mehrere benachbarte Ausschnitte eines Bildes werden zu einem Objekt.

57

CNN (2)

Idee:

• Betrachte nicht von einem Punkt (Neuron) Verbindungen zu allen anderen (Neuronen der dar¨uber liegenden Schicht), sondern nur lokale Gruppen.

• Verwende die gleiche Gewichtsmatrix von allen Punkten aus (Fal- tung)

a b c a b c a b c a b c a b c

CNN (3)

Die Gewichtsmatrizen werden als Filter oder Kernel bezeichnet und es werden mehrere unterschiedliche Filter verwendet, die jeweils zu einer eigenen dar¨uber liegenden Schicht f¨uhren.

2 6 3 8

5 2 1

7 3

1 5 5

a b

d c

2*a+6*b+

1*c+5*d

6*a+3*b+

5*c+5*d

3*a+8*b+

5*c+5*d

1*a+5*b+

3*c+7*d

5*a+5*b+

7*c+1*d

5*a+5*b+

1*c+2*d

4 × 3 Eingangsbild, ein 2 × 2 CNN- Kernels mit den Parametern a,b,c,d, die gelernt werden.

3 × 2 Ausgaben.

59

CNN (4)

• Werden mehrere dieser Faltungsschichten hintereinander geh¨angt, vergr¨oßert sich der Bereich immer weiter, der Einfluss auf das Ergebnis hat.

• N¨utzlich ist es sogenannte Pooling-Schichten zu verwenden, die die Ergebnisse von benachbarten Neuronen zusammenfassen, z.B. den Mittelwert oder den maximalen Wert nehmen und weiter leiten.

2 0 1 7

8 6 1 5

5 2

4

0 6 3

3 1

6 8

6 5

4 × 4 Eingangs- bild, Max-Pooling Schicht, Filter-

maske 2 und

Schrittgr¨oße 2. 2×2 Ausgaben.

CNN (5)

Am Ende gibt es dann

• bei einem Klassifizierungsproblem f¨ur jedes Objekt ein Output- Neuron

• oder z.B. bei einem Segmentierungsproblem, also welches Pixel eines Bildes geh¨ort zu welchem Objekt f¨ur jedes Pixel so viele Output-Neuronen, wie es Klassen gibt.

Viele weitere Details sind f¨ur ein sinnvolles Netz notwendig, aber diese Netze machen auch nichts anderes als eine Kurve an Daten anzupassen.

61

Ausblick (1)

Verbesserungen:

“Intelligentere” Netze und Algorithmen + schnelle Hardware.

• weitere Formen von Faltungsnetzen / rekurrente Netze (mit Zeit- abh¨angingkeit)/ Deep Belief Netze und viele mehr

• Stochastische Modelle

• Verbesserte Gradientenverfahren

• Genetische Algorithmen und anderes zur Netzverbesserung

• ...

• Graphikkarten

Frage: Was lernt das Netz?

Ansatz: R¨uckverfolgung des Gelernten ¨uber die Schichten.

Bei diesen Versuchen hat Google direkt eine neue Kunstrichtung ins Leben gerufen: Inceptionism^∗

∗Computer-Halluzinationen, Spektrum der Wissenschaft, 12/2015, Brian Hayes.

Ausblick (2)

Es fehlen viele “Kleinigkeiten”, die als n¨achstes wichtig f¨ur eine aktu- elle Anwendung, z.B. in der Objekterkennung w¨aren, z.B.:

• Wie sind Faltungsnetze (CNN) in Detail aufgebaut?

• Welche Aktivierungsfunktion ist die geeignetste (LeakyReLU)?

• Welche Fehlerfunktion sollte gew¨ahlt werden (cross entropy)?

• Welchen Lernalgorithmus sollte man nehmen (Adam Algorithmus)?

• Was ist eine gute Initialisierung der Gewichte (Gauß-Verteilung)?

• Wie wird overfitting vermieden (Dropout/L2-Regularisierung/Batch- Norm)?

• ...

Das Anpassen von Kurven an Daten ist nicht trivial, wenn nur wenige Informationen ¨uber die Daten vorliegen, aber meist sehr erfolgreich, wenn viele Daten zur Verf¨ugung stehen!

63