Über die Beschränktheit der Energienorm bei Evolution der Dirac-, Weyl- und Maxwellfelder in gekrümmten Raumzeiten

Über die Beschränktheit der Energienorm bei Evolution der Dirac-, Weyl- und Maxwellfelder in

gekrümmten Raumzeiten

.

Dissertation

zur Erlangung des Grades eines Doktors der Naturwissenschaften

der Fakultät für Mathematik an der Ruhr-Universität Bochum

vorgelegt von Andreas de Vries Bochum, im Oktober 1993

Referent: Prof. Dr. Reinhold Böhme

Korreferent: Prof. Dr. Theodor Schmidt-Kaler Datum der Disputation: 26.01.1994

Veröffentlicht:

Universitätsverlag Dr. N. Brockmeyer, Bochum 1994 (ISBN 978-3-81960-248-1)

Inhaltsverzeichnis

Einleitung 3

1 Spinoren über gekrümmten Raumzeiten 7

1.1 Spinoralgebra . . . 7

1.2 Symmetrische Spinoren . . . 10

1.3 Die Infeld-van der Waerden-Symbole; Spinoren und Welttensoren . . . 11

1.4 Differentiation von Spinoren . . . 17

1.5 Die Beziehung zwischen Spinor- und Tetradenkalkül . . . 20

2 Spinwellen 22 2.1 Uhren und Maßstäbe in der Allgemeinen Relativität . . . 22

2.2 Spinwellenoperatoren über Raumzeiten . . . 25

2.3 Der Dirac-Operator . . . 28

2.4 Masselose Spinwellenoperatoren . . . 34

a) Der Weyl-Operator . . . 34

b) Der Maxwell-Operator . . . 35

3 Anwendungen 40 3.1 Die Kerr-Newman-Raumzeit . . . 40

3.2 Die Robertson-Walker-Kosmen . . . 45

A Anhang 49 A.1 Die Spinkoeffizienten (3.25) der Robertson-Walker-Raumzeit . . . 49

A.2 Thermodynamik Schwarzer Löcher und Superradianz . . . 50

A.3 Der Penrose-Prozeß . . . 54

A.4 Teukolskys Herleitung der Superradianz für die Kerr-Raumzeit (Q= 0) . . . 56

A.5 Spin-Strukturen über Raumzeiten . . . 60

Literaturverzeichnis 61

Einleitung

»Die Anschauungen über Raum und Zeit, die ich Ihnen entwickeln möchte, sind auf experi- mentell-physikalischem Boden erwachsen. Darin liegt ihre Stärke. Ihre Tendenz ist eine radi- kale. Von Stund’ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.« Als Hermann Minkowski [36] mit diesen Worten seinen berühmten Vortrag »Raum und Zeit« am 21. September 1908 in Köln einleitete, wußte noch niemand, daß er durch seine neue geometrische Betrachtungsweise bereits den Keim der Allgemeinen Relativität Einsteins entwickelt hatte. In der Allgemeinen Relativität wird die Raumzeit durch eine vierdimensionale (parakompakte glatte) Mannigfal- tigkeitM beschrieben, die mit einem metrischen Tensorg der Signatur₋2, d.h.(+,−,−,−), versehen ist.

Gerade wegen der »Art Union« von Raum und Zeit haben funktionalanalytische Methoden bisher recht spärlich Anwendung im Rahmen der Allgemeinen Relativität gefunden, im Gegen- satz z.B. zum Fall der Riemannschen Mannigfaltigkeiten mit positiv definiter Metrik. Die vor- liegende Arbeit gibt jedoch hinreichende Kriterien an, für die die aus der Speziellen Relativität wohlbekannten unquantisierten Spinwellengleichungen des Dirac-, Weyl- und Maxwellfeldes, umgeschrieben als Evolutionsgleichungen, in die gekrümmte Welt »hinübergerettet« werden können:

(i) Die vierdimensionale offene Mannigfaltigkeit M ist parallelisierbar; dies sichert die globale Existenz von Spinoren.

(ii) Die zeitartige kontravariante Komponente des metrischen Tensors ist positiv für alle Punkte der zu betrachtenden Karte(U,ϕ),U ⊂M,_ϕ:U →U⊂R⁴, d.h. es gilt

g⁰⁰(x)>0 ∀x∈U.

Dies ist nicht äquivalent zu der in diesem Zusammenhang üblichen Voraussetzung g00(x)>0, wie bereits das Beispiel der Ergosphäre der Kerr-Newman-Raumzeit zeigt, vgl. Gleichung (3.7) und Lemma 3.1. Diese Bedingung ist allerdings unter physikalisch sehr plausiblen Voraussetzungen erfüllt, wie Lemma 2.4 zeigt.

(iii) Die Hyperfläche

Ut=(x⁰=c t=const,x¹,x¹,x³) der KartenumgebungU=ϕ(U⁾ist zusammenhängend.

Mit (i), (ii), und (iii) lassen sich die Spinwellengleichungen für n∈{2, 3, 4} umschreiben zu einer Evolutionsgleichung der Form

∂

∂tψ= −

3

X

ν=1α^ν ∂

∂x^νψ+βψ

mit den vier komplexen (n×n)-Matrizen _α^ν(t,x), _{ν =} 1, 2, 3, _β(t,x) für _ψ∈C₀^∞(Ut,Cⁿ). Bezeichnen wir fürs= ⁿ⁻¹₂ die Operatoren auf der rechten Seite mitL^(s), so ist A:=L⁽³²⁾ der

Dirac-,L⁽¹²⁾der Weyl- undL⁽¹⁾der Maxwell-Operator, und es gilt_∂ψ/∂t=L^(s)ψ.Für jedest bildetC₀^∞(Ut,Cⁿ)mit dem Skalarprodukt

(φ,ψ)s= Z

Ut

φ^∗·ψ·p

gdx¹∧dx²∧dx³,

g = |det(gi j)|, einen Prähilbertraum. In einer gekrümmten Raumzeit sind die Matrizen _α^ν (ν=1, 2, 3) i.a. nicht Hermitesch und bilden damit kein symmetrisches hyperbolisches System nach Friedrichs [38, §6]. In diesen Prähilberträumen lassen sich die Realteile Re (ψ,L^(s)ψ)s

abschätzen, die in gekrümmten Raumzeitennichtverschwinden wie in der flachen Minkowski- Welt. Diese Abschätzungen gelingen im wesentlichen, da für jedesν=1, 2, 3die Matrixα^νals Produkt von zwei Hermiteschen Matrizen dargestellt werden kann. Da nun für die durch das Skalarprodukt(·,·)sinduzierte Normk·k, dieEnergienorm, die Beziehung_∂^∂_tkψk²=³_∂ψ

∂t,ψ´

s+

³ψ,^∂ψ_∂t´

s =2Re³_∂ψ

∂t,ψ´

s gilt, folgt

∂

∂tkψk²=2 Re¡

ψ,L^(s)ψ¢

s.

Als erstes bemerkenswertes Resultat dieser Betrachtungen ergibt sich, daß für die Kerr- Newman-Raumzeit, d.h. einem geladenen rotierenden schwarzen Loch, sowohl der Dirac- als auch der Weyl-Operator dissipativ ist, d.h. Re¡

ψ,L^(s)ψ¢

s 50 gilt, während der Realteil des Maxwell-Operators lediglich durch eine nichtnegative obere Schranke abgeschätzt wer- den kann, die dann und nur dann verschwindet, wenn das schwarze Loch nicht rotiert, Ko- rollare 3.2, 3.3 und 3.4. Dieses Ergebnis stellt eine Verallgemeinerung früherer Arbeiten von Zel’dovich [61] und Teukolsky [55] dar, die für elektromagnetische Wellen bestimmter Moden in der Kerr-Raumzeit einen Verstärkungseffekt, die Superradianz, berechneten, und stimmt mit den Betrachtungen zur Thermodynamik schwarzer Löcher von Hawking [25] überein.

Außerdem ergibt sich, daß sich die Realteile der Operatoren für die Robertson-Walker- Kosmen, der allgemeinen Klasse nicht-stationärer räumlich isotroper Raumzeiten, in einem expandierenden Universum sämtlich als dissipativ erweisen, wobei die Schranken der Energie- norm von der Hubble-Konstanten abhängen.

Die vorliegende Arbeit ist wie folgt gegliedert. Nach einer Idee von Penrose [44], vgl. auch [45], wird im ersten Kapitel der vorliegenden Arbeit für eine parallelisierbare Mannigfaltigkeit mit einigen sehr allgemeinen topologischen Voraussetzungen die Metrik g als Konsequenz der Spin-Struktur hergeleitet. Wesentlich dafür sind die Infeld-van der Waerden-Symbole, die bijektiv mit einer (komplexen) Nulltetrade zusammenhängen, und die eine Art Bindeglieder zwischen der Spinor- und Tensorgeometrie sind.

Im zweiten Kapitel werden mit Hilfe der Infeld-van der Waerden-Symbole die Dirac-, Weyl- und Maxwell-Gleichungen einer gekrümmten Raumzeit konstruiert. Diese Gleichun- gen beschreiben jeweils (unquantisierte) Testfelder mit Spin ¹₂ bzw. 1 in der Mannigfaltigkeit (M^,g). Sie sind lineare Differentialgleichungen erster Ordnung. Unter der Einschränkung an die Koordinaten von M, daß die »zeitartigen« kontravarianten Komponenten von g positiv sind für alle Punkte der Karte,g⁰⁰(x)>0, lassen sich die Spinwellengleichungen umschreiben zu Evolutionsgleichungen. Kern der vorliegenden Arbeit bilden das Lemma 2.8 und die Sätze 2.25, 2.29 und 2.36, mit denen die Realteile der jeweiligen Operatoren abgeschätzt werden können.

Im dritten Kapitel werden die Resultate aus dem vorherigen zunächst auf die Kerr-New- man-Raumzeit angewendet, die ein elektrisch geladenes rotierendes schwarzes Loch darstellt.

Es zeigt sich das bemerkenswerte Resultat, daß der Dirac- und der Weyl-Operator jeweils dissi- pativ ist, während der Realteil des Maxwell-Operators lediglich durch eine nichtnegative obere Schranke abgeschätzt werden kann, die dann und nur dann verschwindet, wenn das schwarze

Loch statisch ist, d.h. nicht rotiert. Dieses Ergebnis ist in voller Übereinstimmung mit früheren Arbeiten von Zel’dovich [61] und Teukolsky [55], die für elektromagnetische Wellen bestimm- ter Moden in der Kerr-Raumzeit einen Verstärkungseffekt, Superradianz, berechneten, und mit den Betrachtungen der Thermodynamik schwarzer Löcher von Hawking [25]. Ferner werden die Realteile der Operatoren für die Robertson-Walker-Kosmen abgeschätzt, die sich in einem expandierenden Universum sämtlich als dissipativ erweisen.

Danksagung

Ich möchte an dieser Stelle dem Land Nordrhein-Westfalen danken, das mit einem Promoti- onsstipendium nach dem Graduiertenförderungsgesetz diese Arbeit unterstützt hat.

Ferner danke ich Herrn Prof. Dr. Böhme für die viele Zeit, die er mir mit Rat und Hilfe zur Seite stand, und für die Geduld, die er so oft behielt, auch wenn er mich schon zielstrebig in die Unwetter des „offenen Wassers“ zusteuern sah. Sehr zu Dank verpflichtet bin ich außerdem Herrn Prof. Dr. Schmidt-Kaler und Herrn Dr. Schulz, bei denen ich Kosmologie lernte, sowie Herrn Prof. Dr. Kaul, der mir durch seine Ansichten zur Kerr-Lösung das Verständnis dieser Raumzeit sehr erleichterte. Dank gebührt nicht zuletzt meinen Kollegen am Lehrstuhl, Mar- tin Müller und Gerald Delvos für die aufschlußreichen und fruchtbaren Diskussionen, sowie Daniela Trompeter für den freundlichen Geist, den sie dem Lehrstuhl verlieh. Katrin Blümel danke ich für all die Unterstützung, die ich bei ihr fand. Sie alle und noch viele Ungenannte leisteten einen unschätzbaren Beitrag zur Vollendung dieser Arbeit.

Kapitel 1

Spinoren über gekrümmten Raumzeiten

Dieses Kapitel liefert eine kurze Einführung in die Analysis der Spinorfelder über einer vierdi- mensionalen parallelisierbaren MannigfaltigkeitM. Es wird ein Spinorbündel konstruiert, das mit Hilfe der Infeld-van der Waerden-Symbole, verallgemeinerten Pauli-Matrizen in krummli- nigen Koordinaten, mit dem Tangentialbündel verknüpft wird. Insbesondere wird die Lorentz- Metrik und die Zeit orientierung abgeleitet von den Infeld-van der Waerden-Symbolen. Diese Idee geht zurück auf Penrose [44], vgl. auch [45]. Schließlich wird das einfache, für die Arbeit jedoch zentrale Lemma 1.29 bewiesen.

1.1 Spinoralgebra

The notion of spinors originates in the observation that a four-vector in Minkowski space can be represented equally by a Hermitean matrix and that a unimodular transformation in the complex two-dimensional space induces a Lorentz transformation in the Minkowski space.

Subrahmanyan Chandrasekhar (1983)

SeiM eine vierdimensionale, parakompakte, offeneC^k-Mannigfaltigkeit,k ∈{2, 3, ...,} [45, p. 212] oder [1, p. 309].M sei ferner zusammenhängend und parallelisierbar, d.h. es existiert ein globaler Schnitt des prinzipalen Vierbein-Bündels(principal four-frame bundle)

(E(M^),p,M^;GL(4,R⁴)).

Bemerkung 1.1. Die topologischen Einschränkungen an die MannigfaltigkeitM, die das Mo- dell eines allgemeinen Gravitationsfeldes, d.h. eineRaumzeit, darstellen soll, sind physikalisch plausibel:

(i) (zusammenhängend) Zwischen Punkten (»Ereignissen«) zweier verschiedener Zusam- menhangskomponenten bestehen keinerlei Wechselwirkungen, sie stellen gewisserma- ßen zwei voneinander unabhängige »Universen« dar.

(ii) (parakompakt)Die Parakompaktheit einer Mannigfaltigkeit ist hinreichend, um auf ihr eine Partition der Eins konstruieren und damit Analysis treiben zu können [13, p. 16].

(iii) (offen)Kompakte Raumzeiten besitzen geschlossene zeitartige Kurven, d.h. Zeitmaschi- nen sind konstruierbar; dies widerspricht jedoch den Konzepten der Kausalität und des freien Willens [26].

(iv) (parallelisierbar) Nach Geroch [20] besitzt eine raum- und zeitorientierbare offene Raumzeit genau dann eine Spin-Struktur, wenn sie parallelisierbar ist.

Folgerung 1.2. Da allgemein ein Prinzipalbündel trivial ist, wenn ein stetiger Schnitt existiert [13, pp. 132], ist das Vierbein-Bündel(E(M^),p,M^;GL(4,R⁴))trivial,

E(M^)∼=M×GL(4,R).

Ferner impliziert die Parallelisierbarkeit vonM bereits ihre Orientierbarkeit [53].

The bundle of frames issolderedto the baseMwhereas in other gauge theories the bundle is rather loosely connected toM.

Andrzej Trautman (1980)

Definition 1.3. Sei x∈M fest. Sei dannS_x^∼_=C² ein zweidimensionaler_C-Vektorraum mit einer symplektischen Bilinearform [·,·] :S_x×S_{x →C}, so daß SL(2,C) isometrisch auf S_x wirkt;S_x heißtSpinorraumüberx. Sei weiterS₌^S_x∈M(x,S_x)∼=M×C², und damit(S,p, M,_C²;SL(2,C))ein (triviales) komplexes Vektorraumbündel, dasSpinorbündel. Die Schnitte dieses Bündels sind Spinorfelder der Valenz ^{h1 0}_{0 0}ⁱoder kontravariante Spinorfelder. SeiS^∗_x der duale Vektorraum vonS_x, und sei(S^∗,p,M,_C²;SL(2,C))mitS^∗₌^S_x∈M(x,S^∗_x)das duale Spinorbündel (Cospinorbündel). Die Schnitte dieses Bündels heißen Spinorfelder der Valenz^{h0 0}_{1 0}ⁱoder kovariante Spinorfelder. Sei {ζ0, ζ1} eine Basis von S_x, die Spinorbasis oderDyade, und sei {ζ⁰,ζ¹} die duale Basis, d.h. es gilt

〈ζ^A,ζB〉:=ζ^A(ζB)=δ^AB. (1.1) In diesen Basen kann ein kontravarianter Spinorξbzw. ein kovarianter Spinorκdurch

ξ=ξ^AζA bzw. _κ=κAζ^A

(A =0, 1; es gilt die Summenkonvention) ausgedrückt werden. Sei_χ:=[ζ0,ζ1]∈Cder Wert des Produkts der Spinorbasis (Es gilt _χ6=0, sonst wären _ζ0 und _ζ1 linear abhängig). Eine normierte Basis, d.h._χ=1, heißtSpinbein (spin-frame).

SeiF₌F₍M) :=C^k(M,C)die Menge derkomplexwertigen SkalarfelderoderSpinorfelder der Valenz^{h0 0}_{0 0}ⁱaufM.

DaS^∼₌M×C²gilt, ist^¡x,{ζ0(x),_ζ1(x)}¢

mit_ζA:M →C²(A=0, 1), ζ0(x)=(1, 0), ζ1(x)=(0, 1),

bereits einC^k-Spinbeinfeld aufM. Insbesondere existiert also ein globaler Schnitt des prinzi- palenSpinbein-Bündels(S,e p,M,_C²;SL(2,C)), mitSe ₌{(x,_τx)|τxSpinbein}.

Definition 1.4. Sei formalS⁰_xder zweidimensionale_C-Vektorraum dergestrichenen Spinoren.

Dann definieren wir die komplexe Konjugation eines (ungestrichenen) Spinors als die Abbil- dungS_x→S⁰_x,_κ7→κ¯, d.h. in Komponenten

κ^A=κ¯^A0∈S⁰_x. (1.2)

Umgekehrt ergibt die komplexe Konjugation eines gestrichenen Spinors einen ungestrichenen [45, p. 106].

Definition 1.5. SeienS^∗_xundS^0∗_x die dualen Räume vonSundS⁰. Seien weiter {_ζ0,_ζ1} und {_ζ^¯₀0,_ζ^¯₁0} jeweils die Basen vonS_x undS⁰_x, und {_ζ⁰,_ζ¹} und {_ζ^¯00, _ζ^¯10} die jeweils dualen Basen vonS^∗_x undS^0∗_x. Dann ist einSpinorder Valenz^{hp q}_{r s} ⁱdie_C-multilineare Abbildung

φ∈S^∗_{x⊗ · · · ⊗}S^∗_x

| {z }

r-mal

⊗S^0∗_{x⊗ · · · ⊗}S^0∗_x

| {z }

s-mal

⊗S_{x⊗ · · · ⊗}S_x

| {z }

p-mal

⊗S⁰_{x⊗ · · · ⊗}S⁰_x

| {z }

q-mal

Bezüglich der Basen {_ζ^A}, {_ζ^¯B0}, {_ζC}, {_ζ^¯_D0} kann ein Spinor der Valenz^{hp q}_{r s} ⁱdurch φ=φA1...ArB₁⁰...Bs⁰

C1...CpD⁰₁...D⁰_qζ^A1⊗ · · · ⊗ζ^Ar⊗ζ^B10⊗ · · · ⊗ζ^B0s⊗ζC1⊗ · · · ⊗ζCp⊗ζD⁰₁⊗ · · · ⊗ζD⁰_q

ausgedrückt werden (die Indizes laufen über 0 und 1 bzw.0⁰ und1⁰). Die Reihenfolge gestri- chener und ungestrichener Indizes kommutiert nicht im allgemeinen, ebenso nicht diejenige von Indizes gleichen Typs [45, p. 123].

Durch die symplektische Bilinearform [·,·] :S_x×S_x→Cwird der ε-Spinor als ein an- tisymmetrischer Spinor der Valenz ^{h0 0}_{2 0}ⁱ definiert,_ε(η,ξ)=[η,ξ]. Die Komponenten des _ε- Spinors,_ε=εABζ^A⊗ζ^B ∈S^∗_x⊗S^∗_x, lauten

εAB=

µ 0 χ

−χ 0

¶

. (1.3)

Entsprechend gilt für seine kontravarianten Komponenten ε^AB=

µ 0 χ⁻¹

−χ⁻¹ 0

¶

. (1.4)

Die lineare Abbildung S_{x →}S^∗_x, _η7→ε(η,·), ist ein Isomorphismus, die Kontraktion. Mit diesem Isomorphismus gilt also _〈κ,ξ〉 =[η,ξ], wobei _κ=ε(η,·). In Komponenten ist also εABη^A=ηb, oder

ηBξ^B=εABη^Aξ^B, (1.5)

d.h. man kann mit demε-Spinor Indizes herunterziehen. Analog kann man mit den Komponen- ten_ε^AB Indizes hinaufziehen. Wegen der Antisymmetrie ist beim Hinauf- und Herunterziehen die Reihenfolge der Indizes wichtig. Merkregel: Beim Herunterziehen eines Indexes den _ε- Spinorhinterund beim Hinaufziehenvordie Komponenten schreiben, also

η^AεAB=ηB, ε^ABηB=η^A, (1.6) Konsequenterweise gilt

ε^ACεC B=ε^AB, εC Aε^{C B}=εAB

, (1.7)

wobeiε^AB= −εBA

=δ_B^A(δ_B^Aist hier das übliche Kronecker-Symbol). Analoges gilt für gestri- chene Indizes,

εA⁰B⁰=εAB, ε^A0B0=ε^AB. (1.8) Die Komponenten desε-Spinors in einem Spinbein lauten

εAB=

µ 0 1

−1 0

¶

(1.9) Weiter gilt für die Kontraktion eines 2-Spinors_φwegen_φAA

=ε^ABφAB und_φ^A_A=ε^{B A}_φAB,

φAA= −φ^AA, (1.10)

und damit allgemeiner diesee-saw-Regelφ...A......A...= −φ...A ...

...

A

..., und insbesondere

ξAξ^A=0. (1.11)

1.2 Symmetrische Spinoren

Eine zentrale Rolle werden die symmetrischen Spinoren spielen. Definieren wir dafür zunächst dieSymmetrisierung

χA...B(C1...Cr)D...E:= 1 r! Ã

X

σ∈Perm(r)χA...Bσ(C1...Cr)D...E

!

(1.12) eines Spinors_χA...B(C₁...C_r)D...E, sowie dieAntisymmetrisierung

χA...B[C1...Cr]D...E:= 1 r! Ã

X

σ∈Perm(r)

signσ χA...Bσ(C1...Cr)D...E

!

(1.13) Beispielsweise gilt für einen 2-SpinorφAB und einen 3-SpinorψABC

φ(AB)=¹₂(φAB+φB A), φ[AB]=¹₂(φAB−φB A), ψ(ABC)=¹₆(ψABC+ψB AC+ψBC A+ψAC B+ψC AB+ψC B A), ψ[ABC]=¹₆(ψABC−ψB AC+ψBC A−ψAC B+ψC AB−ψC B A),

Ein Spinor, der entweder nur obere oder nur untere Indizes besitzt, heißtsymmetrisch, wenn er in seinen ungestrichenen und in seinen gestrichenen Indizes symmetrisch ist [45, p. 132], z.B.

ψA...BC⁰...D⁰=ψ(A...B)(C⁰...D⁰). (1.14) Es ist wohlbekannt, daß jede irreduzible Darstellung vonSL(2,C), also auch vonSO⁺(1, 3), iso- morph ist zu einer Transformationsgruppe auf symmetrischen Spinoren, die durch eine Spin- transformation ξA 7→t_A^BξB gegeben ist. Symmetrische Spinoren sind also irreduzibel unter den GruppenSL(2,C)undSO⁺(1, 3). Sind_φA :=φA...C D⁰...F⁰die Komponenten eines symmetri- schen^{h0 0}_{r s}ⁱ-Spinors, so sind die Transformationen von der Form_{φA 7→φ}A˜=TA˜Aφ_A mit der MatrixTA˜A =tA˜A

·tF˜⁰F⁰, und die_φA transformieren sich gemäß derD(r/2,s/2)-Darstellung der Lorentz-Gruppe [19, 8, 17].

Lemma 1.6. Ist ein Spinor_ψA...BC0...D⁰ der Valenz^{h0 0}_{r s}ⁱsymmetrisch, so hat er(r+1)(s+1) unabhängige komplexe Komponenten.

Beweis. Alle Spinorkomponenten mitr˜ Nullen undr−r˜ Einsen und s˜gestrichenen Nullen unds−s˜gestrichenen Einsen, 05^r˜5^r, 05^s˜5^s, sind gleich; es gibtr+1Möglichkeiten fürr˜unds+1fürs˜.

Wie das illustrative Beispiel eines^{h0 0}_{2 0}ⁱ-Spinors _φAB zeigt, der sich in seinen symmetri- schen und seinen antisymmetrischen Teil aufspalten läßt,

φAB=φ(AB)+φ[AB]=:θAB+λεAB,

λ=¹₂φCC [45, Gl. (2.5.23), p. 106], gilt die Eigenschaft allgemeiner Spinoren [45, p. 140]:

Lemma 1.7. Jeder Spinor _χA...BC0...D⁰ ist die Summe eines symmetrischen Spinors und von Produkten des_ε-Spinors mit Spinoren niedrigerer Valenz.

1.3 Die Infeld-van der Waerden-Symbole; Spinoren und Weltten- soren

Definition 1.8. Definieren wir vier Hermitesche(2×2)-Matrizen_σ^jAB⁰, A=0, 1,B⁰ =0⁰,1⁰, j= 0, 1, 2, 3, durch

σ^jAB⁰=

µ l^j m^j

¯ m^j n^j

¶

(1.15) mitl^j,n^j,m^j ∈F₍M,C), j =0, 1, 2, 3, wobeil,n,m,m¯ linear unabhängig sind, wenn die 4-Tupell=l(x)=(l⁰,l¹,l²,l³),n=n(x)=(n⁰,n¹,n²,n³),m=m(x)=(m⁰,m¹,m²,m³)für jedesx∈M als Vektoren des_C⁴betrachtet werden, dabei notwendigl(x),n(x)∈R⁴wegen der Hermitezität. Ferner seien_σj^AB0 die vier Hermiteschen Matrizen

σjAB⁰

=

µ nj −m¯j

−m¯j lj

¶

(1.16) die den 32 Gleichungen

σⁱAB⁰σjAB⁰

=δji

, σ^jAB⁰σjC D⁰

=εACεB⁰D⁰

=δACδB⁰D⁰. (1.17) genügen. Die acht Matrizen_σ^jAB⁰,_σjAB⁰ heißenInfeld-van der Waerden-Symbole[11, p. 539].

Da M parallelisierbar ist, existieren die Matrizen _σ^jAB⁰ in jedem Punktx∈M, so z. B.

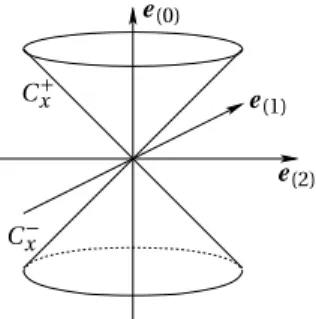
mitl₌e(0)+e(1),n₌e(0)−e(1),m₌e(2)+ie(3), wobei {e(a)|a=0, . . . , 3} ein Vierbein ist. Die Bedingung der Hermitezität liest sich in Komponentenschreibweise wegen(σ^jAB⁰)^∗ =σ^jB A⁰

=σ¯_B^j0A

σ^jAB⁰=σ¯_B^j0A. (1.18)

Lemma 1.9. Das Gleichungssystem (1.17) für die 32 reellen Einträge der Infeld-van der Waerden-Symbole besteht aus höchstens 25 unabhängigen Gleichungen, wenn man voraus- setzt, daßm^jm¯_j∈Rist (ansonsten sind es höchstens 26).

Beweis. Die erste Gruppe der Gleichungen lautet

lⁱnj−mⁱm¯j−m¯ⁱmj+nⁱlj=δⁱ_j, die zweite Gruppe läßt sich schreiben als

3

X

j=0









 l^j m^j

¯ m^j

n^j











·¡

nj,−m¯j,−mj,lj¢

=











1 0 0 0

0 1 0 0

0 0 1 0

0 0 0 1











Beide Gruppen bestehen also aus je 16 Gleichungen. Die zweite Gruppe läßt sich jedoch mit m^jm¯_j∈Rohne Informationsverlust auf das System

3

X

j=0



 l^j m^j

n^j



·¡

nj,−mj,lj¢

=





1 0 0

0 0 0

0 0 1



 (1.19)

reduzieren, denn einerseits ist mitk^jmj =0 auchk^jm¯j =0,k^j ∈{l^j,n^j}, andererseits folgt aus der ersten Gruppe insbesondere l^jnj−m^jm¯j−m¯^jmj+n^jlj =δ^j_j = 4, d.h. mit (1.19) m^jm¯j+m¯^jmj=l^jnj +n^jlj −4_{= −}2, alsom^jm¯j = −1.

Definition 1.10. Einkomplexer^hr_sⁱ-Welttensorist ein Spinor der Valenz^{hr r}_{s s}ⁱ, d.h. ein Spinor mit Komponenten der Form_χ^{AB0...C D0}_{E F}0...G H⁰.

Definition 1.11. Ein komplexer Welttensor, der invariant gegenüber der komplexen Konjuga- tion ist,

χ^{AB0...C D0}E F⁰...G H⁰=χ¯^B0A...D0CF⁰E...H⁰G

heißtreeller Welttensor. Die Menge der reellen Welttensoren bezeichnen wir mit T_{x ⊗ · · · ⊗} T_{x ⊗}T^∗_{x ⊗ · · · ⊗}T^∗_x; insbesondere istT_{x ⊂}S_{x ⊗}S⁰_x.

Sei {_ζ(0),_ζ(1)} ein globaler Schnitt des Spinbeinbündels. Für die Komponenten_ζ(A)B, A, B = 0, 1, gilt wegen_ζ(A) = ζ(A)Bζ(B) natürlich _ζ(A)B

=δAB. Da {_ζ(0), _ζ(1)} eine normierte Spinorbasis ist, sieht man sofort

ζ(A)Cζ(B)C=εAB, ζ(A)Cζ^(B)C=εAB, ζ^(C)Aζ(C)B=εAB, (1.20) d.h. man kann die Klammern weglassen, und die oben entwickelte Spinoralgebra bleibt kon- sistent. Diese Konsistenz wird nur durch die Beziehungen_ε(A)(B)=εAB und_ε(A)(B)

=εAB ga- rantiert; für eine nichtnormierte Spinorbasis müssen die Klammern zur Markierung der Spin- beinindizes bleiben [11, §102]. Dasselbe gilt für das komplex konjugierte Spinbein {_ζ^¯₍₀0),_ζ^¯₍₁0)} bzw. für dessen Komponenten_ζ^¯A⁰B⁰.

Als komplexe Vektoren geschrieben lauten die Spinbeinkomponenten ζ0A

=(1, 0), ζ0A

=(0, 1), ζ¯0⁰A⁰

= µ1

0

¶

, ζ¯1⁰A⁰

= µ0

1

¶ . Beachte, daß wegen_ζBA

=εC Bζ^{C A}gilt:_ζ0A= −ζ^1Aζ1A

=ζ^0A, und analog_ζ^¯0⁰A⁰= −ζ^10A0ζ¯1⁰A⁰

= ζ^00A0. Damit sieht man sofort die Beziehungen

l^j =σ^jAB⁰ζ0Aζ¯0⁰B⁰, m^j=σ^jAB⁰ζ0Aζ¯1⁰B⁰, m¯^j =σ^jAB⁰ζ1Aζ¯0⁰B⁰

, n^j=σ^jAB⁰ζ1Aζ¯1⁰B⁰

, l_j =σjAB⁰ζ⁰Aζ¯⁰⁰B⁰, m_j=σjAB⁰ζ⁰Aζ¯¹⁰B⁰,

m¯j =σjAB⁰ζ¹Aζ¯⁰⁰B⁰, nj=σjAB⁰ζ¹Aζ¯¹⁰B⁰, (1.21) oder in Matrizenschreibweise

l^j=(1, 0)

µ l^j m^j

¯ m^j n^j

¶ µ1 0

¶

, m^j=(1, 0)

µ l^j m^j

¯ m^j n^j

¶ µ0 1

¶

, etc.

Satz 1.12. Seix∈M, und seiTxM der Tangentialraum vonM anx. Dann ist der Raum der reellen WeltvektorenT_xisomorph zum Tangentialraum,T_x ^∼₌TxM.

Beweis. Sei {_ζ0,_ζ1} ein Spinbein, und sei {_ζ^¯₀0,_ζ^¯₁0} das komplex konjugierte Spinbein. Dann ist {_ζ0⊗ζ^¯₀0,_{ζ0 ⊗ζ}^¯₁0,_ζ1⊗ζ^¯₀0,_ζ1⊗ζ^¯₁0} eine Basis vonS_{x ⊗}S⁰_x, d.h.S_x⊗S⁰_x ^∼_=C⁴. Die Komponenten eines reellen Welttensors_χbilden wegen der Reellitätsbedingung_χ^AB0=χ¯^AB0 eine Hermitesche Matrix, d.h.T_x ist isomorph zu dem reellen Vektorraum der Hermiteschen (2×2)-Matrizen. Die vier Infeld-van der Waerden-Symbole_σ^jAB⁰ bilden nun eine Basis dieses Vektorraums, die wiederum durch die Projektionen_σ^j00⁰ 7→l^j,_σ^j01⁰ 7→m^j,_σ^j10⁰7→m¯^j,_σ^j11⁰

7→n^j, bijektiv auf die reellen Vektoren T^j= 1

p2

³

l^j+n^j´

, X^j= 1

p2

³

m^j+m¯^j´ , Y^j= 1

p2i

³

m^j−m¯^j´

, Z^j= 1

p2

³

l^j−n^j´

(1.22)