Seminararbeit aus Analysis TU-Wien 2014/2015
Die Invarianzs¨atze von Brouwer
David Kofler
19. Januar 2014
Inhaltsverzeichnis
1 Einleitung 3
2 Grundlagen 3
3 Die Invarianzs¨atze von Brouwer 4
Diese Seminararbeit besch¨aftigt sich mit den zwei S¨atzen Invariance of domain und Invariance of dimen- sion von Brouwer:
Satz 1.1 (Invariance of domain). Sei U eine offene Teilmenge von Rn und f : U → Rn stetig und injektiv. Dann ist f(U)offen.
Satz 1.2 (Invariance of dimension). Seien U ⊂ Rn und V ⊂ Rm nicht leer und offen mit m ≤ n.
Existiert eine stetige und injektive Funktion f : U →V, dann folgt n=m. Insbesondere sind Rn und Rmnicht hom¨oomorph f¨ur n6=m.
Auf dem ersten Blick scheint die Tatsache, dassRn undRm f¨ur n6=mnicht hom¨oomorph sind, trivial zu sein. Tats¨achlich gibt es stetige und surjektive, aber nicht injektive, Funktionenf :R→Rn, die von Peano 1890 entdeckten “Peano Kurven”. Also ist die Aussage nicht mehr so offensichtlich, dass es keine Hom¨oomorphismen zwischenRundRngeben kann. Erst 1911 konnte Brouwer beweisen, dass es wirklich keine Hom¨oomorphismen gibt. Der historisch interessierte Leser sei auf Chapter II in [3] verwiesen.
Normalerweise werden diese S¨atze mit der Maschinerie aus der algebraischen Topologie bewiesen. Wir werden einen analytischen Beweis angeben, der bis auf den Fixpunktsatz von Brouwer, ohne Resultate aus der algebraischen Topologie auskommt. Dazu kombinieren wir eine Arbeit von Wlasyslaw Kulpa [1]
(1998) und von Terence Tao [2] (2011).
2 Grundlagen
Im Folgenden bezeichnen wir mit Un(x) bzw. Kn(x) die offene bzw. abgeschlossene Kugel um xmit Radius >0 inRn. MitK1n bezeichnen wir die abgeschlossene Einheitskugel um 0 inRn.
Bemerkung 2.1.N ⊂Rn ist Lebesgue-Nullmenge, d.h.λn(N) = 0, genau dann, wenn f¨ur jedes >0 eine Folge von Quadern (Qk)k∈Nexistiert, sodass
N ⊂
∞
[
k=1
Qk und
∞
X
k=1
λn(Qk)< .
Satz 2.2. Sei B ⊂Rn offen,A ⊂B eine Lebesgue-Nullmenge und f :B →Rn stetig differenzierbar.
Dann istf(A)eine Lebesgue-Nullmenge.
Beweis. SeiQ⊂B ein abgeschlossener Quader. Es gen¨ugt zu zeigen, dassf(A∩Q) eine Nullmenge ist, da sichB als Vereinigung von abz¨ahlbar vielen solcher abgeschlossenen Quadern schreiben l¨asst.
Der QuaderQist kompakt. Also ist die Ableitung aufQdurch einC >0 beschr¨ankt:
kDf(x)kop:= sup
v∈Rn
{|Df(x)·v|:kvk ≤1} ≤ C, x∈Q.
SeienQundCim Folgenden fest. DaQkonvex ist, ist mitx, y∈Qauch die gesamte Verbindungsstrecke xyin Qenthalten und somit auch inB. Mit
f(y)−f(x) = Z 1
0
Df(x+t(y−x))(y−x)dt folgt
kf(y)−f(x)k∞=
Z 1
0
Df(x+t(y−x))(y−x)dt ∞
≤ Ck(y−x)k∞.
Jetzt verwenden wir, dassAeine Nullmenge ist. Sei also >0 und (Wk)k∈Neine Folge von W¨urfeln mit Mittelpunktak und L¨angedk, d.h.Wk =
x∈Rn:kx−akk∞< d2k , sodass A∩Q⊂
∞
[
k=1
Wk und
∞
X
k=1
λn(Wk) =
∞
X
k=1
dnk < .
F¨urx∈Wk gilt
kf(x)−f(ak)k∞ ≤ Ckx−akk∞ < Cdk
2 .
Also liegt f(Wk) in einem W¨urfel Wk0 mit L¨ange d0k ≤Cdk und Volumen λn(Wk0) ≤ (Cdk)n. Da die MengeA∩Qvon der Folge (Wk)k∈Nuberdeckt wird, gilt¨ f(A∩Q)⊂S∞
k=1Wk0 und somit folgt f¨ur das Maß
λn(f(A∩Q)) ≤
∞
X
k=1
λn(Wk0) ≤ Cn
∞
X
k=1
dnk ≤ Cn.
Da >0 beliebig war, istf(A∩Q) eine Nullmenge.
Wir brauchen folgende Aussagen, die ohne Beweis angegeben sind.
Satz 2.3 (Fortsetzungssatz von Tietze). Sei (X,T) ein normaler Raum, d.h. zu je zwei disjunkten abgeschlossenen Mengen A ⊂X und B ⊂X existieren zwei offene Mengen OA ∈ T und OB ∈ T mit A⊂OA,B ⊂OB undOA∩OB =∅. Sei A⊂X abgeschlossen undf :A→Reine stetige reellwertige Funktion. Dann existiert eine stetige FortsetzungF :X →RmitkFk∞=kfk∞ und F|A=f.
Satz 2.4. Metrische R¨aume sind normal.
Satz 2.5(Stone-Weierstrass). IstAeine Algebra stetiger reeller Funktionen auf einem kompakten Raum X, die punktetrennend ist und die die konstante Funktion1enth¨alt, dann liegtA dicht inC(X,R)bzgl.
der Supremumsnorm.
3 Die Invarianzs¨ atze von Brouwer
Nun kommen wir zu den zwei Haupts¨atzen dieser Seminararbeit. Wie bereits bemerkt, spielt der folgende Satz eine wichtige Rolle im Beweis der Invarianzs¨atze:
Satz 3.1(Fixpunktsatz von Brouwer). Seif :K1n →K1n eine stetige Funktion auf der abgeschlossenen Einheitskugel K1n :={x∈Rn:kxk2≤1}. Dann hat f mindestens einen Fixpunkt, d.h. es existiert ein x∈K1n mitf(x) =x.
F¨ur den Beweis sei auf Satz 7.2.4 in [5] verwiesen.
Seif :K1n→Rn stetig und injektiv, dann ist die Einschr¨ankungf :K1n→f(K1n) eine stetige Bijektion zwischen zwei kompakten Hausdorff-R¨aume, also ein Hom¨oomorphismus. Insbesondere istf−1:f(K1n)→ K1n stetig. Mit dem Fortsetzungssatz von Tietze Satz 2.3 finden wir komponentenweise eine stetige FortsetzungG:Rn→Rn vonf−1. Die AbbildungGeingeschr¨ankt auff(K1n) hat genau eine Nullstelle, n¨amlich beif(0). Mit dem Fixpunktsatz von Brouwer Satz 3.1 k¨onnen wir nun zeigen, dass diese Nullstelle in einem gewissen Sinn stabil ist.
Lemma 3.2 (Stabilit¨at). Sei f :K1n → f(K1n) ein Hom¨oomorphismus undG: Rn →Rn eine stetige Fortsetzung vonf−1:f(K1n)→K1n. Weiters sei H :f(K1n)→Rn eine stetige Funktion, sodass
kG(y)−H(y)k2≤1 f¨ur alle y∈f(K1n).
Dann hat H mindestens eine Nullstelle, d.h. es existiert einy∈f(K1n), sodass H(y) = 0.
Beweis. Betrachte die stetige Funktion
ψ(x) :=x−H(f(x)) =G(f(x))−H(f(x)), x∈K1n.
Nach Voraussetzung giltkG(y)−H(y)k2 ≤1 f¨ur y ∈f(K1n). Also istψ(x) eine stetige Abbildung von K1n nachK1n. Nach Satz 3.1 hatψ(x) einen Fixpunktx0, womit
x0=ψ(x0) =x0−H(f(x0)).
Also giltH(y) = 0 f¨ury=f(x0).
G:Y →Rn eine stetige Funktion mit G(y)6= 0 f¨ur y∈Y1. Dann existiert zu jedem δ >0 eine stetige Funktion Q:Y →Rn, sodass
kG(y)−Q(y)k∞< δ
undQ(y)6= 0f¨ur alley∈Y gilt.
Beweis. W¨ahleη∈Rmit 0<2η < δ, sodass
G(Y1)∩U2η(0) =∅.
Das ist m¨oglich, da 0∈/G(Y1),Y1 kompakt undGstetig ist. DaY kompakt ist, finden wir mit Satz 2.5 Polynome inn-Ver¨anderlichenP1, . . . , Pn :Rn→R, sodass
kG(y)−P(y)k∞< η/√
n f¨ur alley∈Y,
wobei P = (P1, . . . , Pn)T : Y → Rn ist. Nach Satz 2.2 istP(Y2) eine Nullmenge. Somit existiert ein d∈Uη(0)\P(Y2). F¨ur das verschobene Polynom
Q(y) :=P(y)−d giltQ(y) = 0 genau dann, wennd∈P(Y2), womit 0∈/Q(Y2).
F¨ur einy∈Y1gilt
kG(y)−Q(y)k2 = kG(y)−P(y) +dk2 ≤ kG(y)−P(y)k2+kdk2
≤ √
nkG(y)−P(y)k∞+kdk2 < η+η= 2η < δ.
WegenG(Y1)∩U2η(0) =∅schließen wir auf 0∈/Q(Y1).
Proposition 3.4. Seif :K1n →Rn stetig und injektiv. Dann liegt f(0)im Inneren vonf(K1n).
Den Beweis f¨uhren wir durch Widerspruch. Wir nehmen an,f(0) sei nicht im Inneren von f(K1n). Aus dieser Tatsache konstruieren wir uns eine nullstellenfreie St¨orungH der stetigen FortsetzungGvonf−1, die klein genug ist, um die Voraussetzungen von Lemma 3.2 zu erf¨ullen.
Beweis. Angenommen f(0) sei nicht im Inneren von f(K1n). SeiG :Rn →Rn die stetige Fortsetzung vonf−1 wie in Lemma 3.2.
W¨ahle >0, sodass|G(y)| ≤0.1 f¨urky−f(0)k2 ≤2. Das ist m¨oglich, da f(0) eine Nullstelle von G ist.
Daf(0) nicht inf(K1n)◦ist, existiert einc∈f(K1n)c, sodasskf(0)−ck2< . Mit der Dreiecksungleichung folgt
kG(y)k2≤0.1 f¨ur ky−ck2≤. (1) Betrachte die MengeY :=Y1∪Y2, wobei
Y1:={y∈f(K1n) :ky−ck2≥} und Y2:={y∈Rn :ky−ck2=}.
Nach Konstruktion sind Y und Y1 kompakt. Y enth¨alt nicht den Punkt f(0), da kf(0)−ck2 < ist.
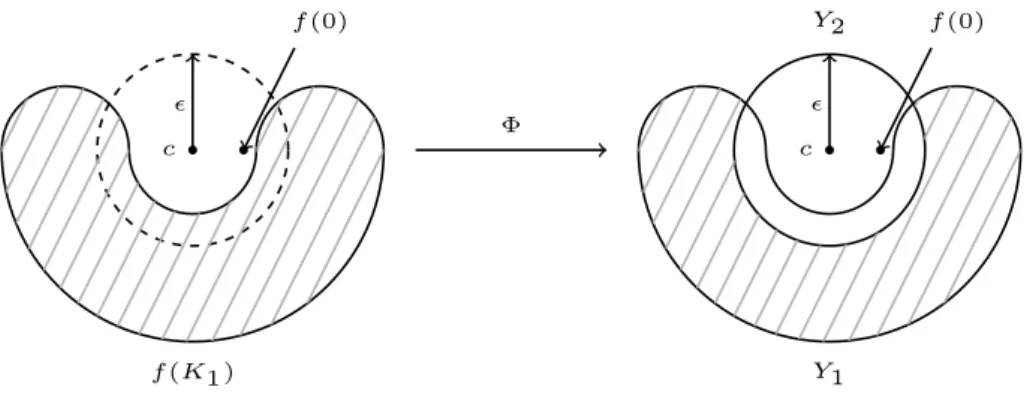
Insbesondere enth¨alt Y1 keine Nullstellen von G. Weiters betrachten wir die Funktion Φ :f(K1n)→Y definiert durch
Φ(y) := max(
ky−ck2,1) (y−c) +c, (2)
siehe Abbildung 1. Diese ist stetig und wohldefiniert, da der Punkt c nicht inf(K1n) liegt. Der Punkt Φ(y) liegt in Y f¨ur alley∈f(K1n), da f¨urky−ck2>
Φ(y) =y∈f(K1n) und kΦ(y)−ck2=ky−ck2≥
c
f(0)
f(K1 )
Φ
c Y2 f(0)
Y1
Abbildung 1: Die Abbildung Φ verschiebt alle Punkte innerhalbUn(c) nach außen.
gilt und f¨urky−ck2≤
kΦ(y)−ck2=.
DaY kompakt ist, finden wir mit Lemma 3.3 eine stetige FunktionQ:Y →Rn mit 0∈/ Q(Y) und kG(y)−Q(y)k2<0.7 f¨ur alle y∈Y. (3) Wir definieren nunH :f(K1n)→Rn durch
H(y) :=Q(Φ(y)).
Als Zusammensetzung von zwei stetigen Funktionen istH stetig und besitztkeineNullstellen inf(K1n).
Um den Abstand zuGabzusch¨atzen, unterscheiden wir f¨ury∈f(K1n) folgende zwei F¨alle:
1. ky−ck2> :
Wegen Φ(y) =y und mit (3) erhalten wir
kG(y)−H(y)k2<0.7.
2. ky−ck2≤:
Wegen kΦ(y)−ck2=und (1) gilt
kG(Φ(y))k2≤0.1.
Mit (3) und der Dreiecksungleichung folgt
kG(y)−H(y)k2 = kG(y)−G(Φ(y)) +G(Φ(y))−Q(Φ(y))k2
≤ kG(y)k2+kG(Φ(y))k2+kG(Φ(y))−Q(Φ(y))k2 ≤ 0.9.
Also erhalten wir insgesamt
kG(y)−H(y)k2≤1 f¨ur y∈f(K1n). (4) Somit sind die Voraussetzung von Lemma 3.2 erf¨ullt. Also m¨ussteH mindestens eine Nullstelle besitzen.
Da wir aberH nullstellenfrei konstruiert haben, erhalten wir einen Widerspruch.
Satz 3.5 (Invariance of domain). Sei U eine offene Teilmenge von Rn und f : U → Rn stetig und injektiv. Dann ist f(U)offen.
liegt. DaU offen ist, finden wir eine KugelKrn(u), die ganz inU liegt mit 0< r≤1, sodassf aufKr(u) stetig und injektiv ist. Aufgrund von Translationsinvarianz k¨onnen wir die Funktion ˜f(x) :=f(rx+u) betrachten, die ebenso stetig und injektiv ist und zwar auf K1n. Nach Satz 3.4 liegt ˜f(0) = f(u) im Inneren von ˜f(K1n(0)) = f(Krn(u)). Somit existiert ein > 0, sodass Un(f(u)) ⊂ f(U). Da u ∈ U beliebig war, istf(U) offen.
Korollar 3.6 (Invariance of dimension). Seien U ⊂Rn und V ⊂Rm nicht leer und offen mit m≤n.
Existiert eine stetige und injektive Funktion f : U →V, dann folgt n=m. Insbesondere sind Rn und Rmnicht hom¨oomorph f¨ur n6=m.
Beweis. Angenommen m < n und es existierte eine stetige und injektive Abbildung f. Definiere g : U → Rn als g := ι◦f, wobei ι : Rm → Rn die stetige und injektive Einbettung ι((x1, . . . , xm)) :=
(x1, . . . , xm,0, . . . ,0) ist. Die Menge g(U) ist von der Form (f1(x), f2(x), . . . , fm(x),0, . . . ,0) und hat somit leeres Inneres. Da die Funktiong aber stetig und injektiv ist, muss im Widerspruch dazu, g(U) nach Satz 3.5 offen sein.
Also haben wir bewiesen, dass Rn und Rm f¨ur n 6= m nicht hom¨oomorph sein k¨onnen, da es keine Hom¨oomorphismen zwischen Rn und Rm gibt. F¨ur n = 1 und m > 1 kann man das direkt zeigen.
Denn angenommen es existiert ein Hom¨oomorphismusf :R→Rm, dann k¨onnen wir den Punkt 0 und f(0) rausnehmen, und wir haben immer noch einen Hom¨oomorphismus ˜f :R\ {0} →Rm\ {f(0)}. Da Rm\ {f(0)}zusammenh¨angend ist undR\ {0}nicht, k¨onnen sie nicht hom¨oomorph sein.
Bemerkung 3.7.Eine Verallgemeinerung von Satz 3.5 auf Banachr¨aume:
Satz:SeienX, Y Banachr¨aume undU ⊂X offen. Istf :U →Y lokal injektiv und l¨asst sich als Summe von zwei Funktion f =g+hschreiben. Wobei g Fredholm mit Index0 und hstetig und lokal kompakt.
Dann istf(U)offen.
F¨ur den Beweis sei auf Corollary 2.2 in [4] verwiesen.
Außerdem spielt Satz 3.5 im Beweis des 5. Hilbert Problems eine wichtige Rolle (siehe [2]):
Satz:Jede lokal euklidische Gruppe ist isomorph zu einer Lie-Gruppe.
Literatur
[1] Wladyslaw Kulpa: Poincar´e and domain invariance theorem, Acta Universitatis Carolinae. Ma- thematica et Physica,http://dml.cz/dmlcz/702050, Vol. 39 , No. 1-2, 127–136, 1998.
[2] Terence Tao: Brouwer’s fixed point and invariance of domain theorems, and Hilbert’s fifth problem, http://terrytao.wordpress.com/2011/06/13/
brouwers-fixed-point-and-invariance-of-domain-theorems-and-hilberts-fifth-problem, UCLA, 2011.
[3] Jean Dieudonn´e: A History of Algebraic and Differential Topology, 1900-1960, Birkh¨auser, 1989.
[4] Alessandro Calamai: The Invariance of Domain Theorem for compact perturbations of nonlinear Fredholm maps of index zero, Nonlinear Functional Analysis and Applications 9, 185-194, 2004.
[5] Martin Bl¨umlinger: Analysis 3, http://www.asc.tuwien.ac.at/~blue/Ana3.pdf, Skriptum, TU Wien, WS 2013.