A point particle of mass m is moving under the influence of gravity and without friction on a paraboloid surface of the form z = µ ¡

Mechanik Solution 4.

HS 2019 Prof. Gino Isidori

Exercise 1. Point mass on a paraboloid

A point particle of mass m is moving under the influence of gravity and without friction on a paraboloid surface of the form z = µ ¡

x

+ y

¢

shown in Figure 1.

(a) Find the Lagrangian of the system using cylindrical coordinates and express the constraint through a Lagrange multiplier. Afterwards, derive the equations of motion for the particle.

(b) The Lagrangian found in a) has a rotational symmetry. Apply Noether’s theorem to derive the con- served quantity associated to it. Compare your result with the Euler-Lagrange equations derived before.

(c) Show that for each fixed value of the conserved quantity, there exists a special solution to the Euler- Lagrange equations with constant radius of motion r(t) = r

= const.

(d) We will now investigate small perturbations to the above solution, i.e. nearly circular orbits. For this, expand the equations of motion around r

using r(t) = r

+δ r(t) with a small perturbation δ r, where we have

0

¿ 1. Now, find the solution for δ r(t).

Hint: After inserting the expansion into the equations of motion you can simplify the result using (1 +

)

= 1 + n

0

+ O µ

r²₀

¶

. Throughout your calculation only work up to first order in

0

, meaning that you can set all terms of the form δ r

with k ≥ 2 to zero. In the end the motion of δ r should turn out to be the one of a harmonic oscillator.

Figure 1: Point mass constrained to move on a paraboloid surface.

Solution.

(a) In Cartesian coordinates the kinetic energy T, the potential energy V and the constraint f read

T = 1 2

¡ x ˙ ² + y ˙ ² + z ˙ ² ¢ , V = m gz,

f = µ ¡

x ² + y ² ¢

− z = 0. (S.1)

Therefore the Lagrangian is given by L = T − V − λ f = 1

2

¡ x ˙ ² + y ˙ ² + z ˙ ² ¢

− m gz − λ £ µ ¡

x ² + y ² ¢

− z ¤

, (S.2)

where _λ is a Lagrange multiplier. Transforming to cylindrical coordinates ¡ r, _φ , z ¢

using x = r cos _φ ,

y = r sin _φ ,

z = z (S.3)

we find a simpler form of the Lagrangian L = 1

2 m ¡

˙

r ² + r ² _φ ˙ ² + z ˙ ² ¢

− m gz − λ ¡

µ r ² − z ¢

. (S.4)

Now we derive the Euler-Lagrange equations using

∂ L

∂ q _i − d dt

∂ L

∂ q ˙ _i = 0 (S.5)

for q _i = r, _φ , z, _λ . This yields the four equations of motion 0 = m r ¨ − m _φ ˙ ² r + 2 _λµ r, 0 = d

dt

¡ mr ² _φ ˙ ¢ , 0 = m z ¨ + m g − λ ,

0 = µ r ² − z, (S.6)

where the last one is again the constraint.

(b) The paraboloid has a rotational symmetry in the z-direction. Such a rotation corresponds to a shift in the _φ -coordinate

φ → φ ⁰ = φ + ² (S.7)

whereas the other coordinates r and z stay unchanged. Since _φ is a cyclic variable and _² is a constant shift, the Lagrangian is invariant under the given transformation. Thus, we can apply Noether’s theorem

L _z = ^∂ L

∂ _φ ˙ 0

d _φ ⁰

d _² = mr ² _φ ˙ , (S.8)

where we used ^dφ _{d ²}

= 1. Hence, the z-component of the angular momentum is conserved.

Comparing with the equations of motion derived above we see that the conservation of L _z is equivalent to the second of equations (S.6).

(c) The last three equations of motion from (S.6) can be rewritten as

L _z = mr ² _φ ˙ = const.,

Using these we can rewrite the first of equation (S.6) as 0 = − r ³ r ¨ + L ² _z

m ² − 2 _µ r ⁴ £ g + 2 _µ ¡

˙ r ² + r r ¨ ¢¤

. (S.10)

We can no insert our ansatz r(t) = r ₀ = const., which yields

L ² _z = 2 _µ m ² gr ⁴ ₀ (S.11)

showing that for every fixed value of L _z there is a solution to the equations of motion with fixed radius r ₀ describing circular orbits.

(d) We now look at small perturbations around the circular orbit derived above. For this we insert the ansatz r(t) = r ₀ + δ r(t) with ^δ _r ^r

0

¿ 1 into equation (S.10). Using the expansion given in the hint we obtain

0 = − r ² ₀ (r ₀ + 3 _δ r) ¨ _δ r + L ² _z

m ² − 2 _µ r ³ ₀ (r ₀ + 4 _δ r) n

g + 2 _µ h

δ ˙ r ² + (r ₀ + δ r) ¨ _δ r io

. (S.12)

Only keeping terms up to order one in _δ r then yields 0 = − r ³ _{0 δ} ¨ r + L ² _z

m ² − 2 _µ gr ⁴ ₀ − 8 _µ gr ³ _{0 δ} r − 4 _µ ² r ⁵ _{0 δ} ¨ r. (S.13) Using the solution for constant radius in equation (S.11) we find that the second and third term in the above expression cancel. This gives as result the radial equation of motion

0 = _δ ¨ r + 8 _µ g

1 + 4 _µ ² r ² ₀ ^δ r, (S.14)

which is describing a harmonic oscillator with frequency _ω =

r 8 µ g

1 + 4 µ

r

. The solution of this differential equation can be derived with the ansatz

δ r(t) = A sin( _ω t + c), (S.15)

where A and c are constants depending on the initial conditions. Note that we need A ¿ r ₀ for our approximations to hold.

Exercise 2. Two particles connected by a string.

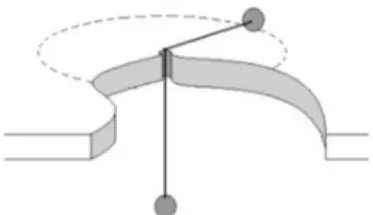
Consider two particles of equal mass m connected by a string of length L. One of them is suspended through a hole in a table and the other one moves on the frictionless top of a plane, see Figure 2. Both particles are subject to the action of gravity. Assume that the suspended particle moves only in the vertical direction.

(a) Determine the symmetries of the system. Which are the corresponding conserved quantities?

(b) Obtain the Lagrangian of the system. Use Lagrangian multipliers to determine the constraint force(s).

(c) Find the configuration for which the system is in equilibrium.

Figure 2: Mechanical system of exercise 2.

Solution.

(a) The system described above presents the following symmetries:

i) The motion of the system is time invariant, i.e. none of the forces explicitly depend on time. From the Noether theorem this implies that the energy of the system is a conserved quantity.

ii) The system is also invariant under rotations of the particle sitting in the plane around the z axis. As was derived in class, in this case the Noether theorem implies that the z component of the angular momentum is conserved for the particle in the plane.

(b) We use the following coordinates to describe the two particles (we label the particle in the plane as particle 1)

x ₁ = r cos _φ x ₂ = 0 , y ₁ = r sin _φ y ₂ = 0 , z ₁ , z ₂ = z ,

(S.16)

where we choose the z-axis to point downwards. Furthermore, the string and the plane impose the following holonomic constraints

r + z − L = 0 , z ₁ = 0 . (S.17)

The second constraint imposes a trivial condition and yield to a constraint force opposite to the gravitational force acting on the body sitting in the plane. For simplicity, we will use Lagrangian multipliers only for the first constraint.

The kinectic energy reads

T = 1 2 m ¡

˙

x ₁ ² + y ˙ ₁ ² + z ˙ ² ₁ + x ˙ ² ₂ + y ˙ ² ₂ + z ˙ ₂ ² ¢

= 1 2 m ¡

˙

r ² + r ² _φ ˙ ² + z ˙ ² ¢ .

(S.18)

For the potential energy we fix the origin at the plane, we thus have

V = − m gz ₂ = − m gz . (S.19)

Combining these two, together with the constraint, we find the Lagragian of the system L 1

m ¡

˙

r ² r ² _φ ˙ ² z ˙ ² ¢

m gz _λ (r z L) . (S.20)

We use the Euler-Lagrange equations to obtain the equations of motion m r ¨ − mr _φ ˙ ² − λ = 0 ,

d dt

¡ mr ² _φ ˙ ¢

= 0 =⇒ mr ² _φ ˙ = L _z = const. , m z ¨ − m g − λ = 0 ,

(S.21)

plus the constraint: _` + r − L = 0. The second equation is no more than angular momentum conservation in the ˆ z direction. Substituting in the first equation we thus have

m¨ r − L ² _z

mr ³ − λ = 0 , m z ¨ − m g − λ = 0 .

(S.22)

From the equations above it is clear that the forces of constraint are

~ F ₁ ^const = (m z ¨ − m g) ˆ e _r ,

~ F ₂ ^const = µ

m r ¨ − L ² _z mr ³

¶ ˆ e _z ,

(S.23)

and we have | F ~ ₁ ^const | = | ~ F ₂ ^const | .

(c) The system will be in equilibrium when the forces of constraint compensate the centrifugal and gravitational forces, so that ¨ r = z ¨ = 0. From (S.22), it is clear that this happens when λ = m g = L ² _z /(mr ³ ). Solving for this we obtain the radius for which the system presents a stable configuration

r _eq = µ L ² _z

m ² g

¶

1 3

. (S.24)