Vektorräume und Lineare Abbildungen

Vektorräume und Lineare Abbildungen

Patricia Doll, Selmar Binder, Lukas Bischoff, Claude Denier ETHZ D-MATL SS–07

11.04.2007

1 Vektorräume

1.1 Definition des Vektorraumes (VR)

1.1.1 Grundoperationen

Um den Vektorraum zu verstehen müssen wir erst die Grundoperationen die angewen- det werden beschreiben (hier am Beispiel der „geometrischen“ Vektoren, für andere mögliche Elemente eines Vektorraumes müssen sie sinnvoll definiert werden):

1. Addition zweier Vektoren

Vektoren werden gemäss dem ”altbekannten” Parallelogramm addiert.

Abbildung 1: Vektoraddition

2. Multiplikation mit einem Skalar:

Bei der Multiplikation eines Vektors mit einem Skalar a (d.h. einer eindimensiona- len Zahl) bleibt die Richtung des Vektors erhalten. Nur die Länge wird gestreckt wobei a der Streckungsfaktor ist.

Dabei gelten immer folgende Rechenregeln:

(~a,~b, ~csind Vektoren, α, β Skalare Zahlen) i) ~a+~b=~b+~a

ii) ~a+ (~b+~c) = (~a+~b) +~c iii) ~a+~0 =~0

iv) ~a+ (−a) =~ ~0 v) α(β~a) = (αβ)~a

vi) (α+β)~a=α~a+β~a α(~a+~b) =α~a+β~b vii) 1·~a=~a

1.1.2 Definition Vektorraum

Ein Vektorraum ist eine Menge von Elementen (Vektoren), die bezüglich der definierten Grundoperationen abgeschlossen ist. Das heisst, Elemente eines Vektorraumes unter- einander oder mit einem Skalar verknüpft ergeben wieder ein Element desselben VR.

Somit sind Vektorräume bezüglich der Grundoperationen Abelsche Gruppen.

Bemerkung: Elemente eines Vektorraums können nicht nur „geometrische“ Vektoren sein. Es kann sich beispielsweise auch um Matrizen oder Funktionen handeln. Es müs- sen nur die Grundoperationen neu definiert werden. Für Funktionen zum Beispiel ist es nahe liegend unter der Multiplikation mit einem Skalar die Streckung der Funktions- werte zu verstehen. Auch die Addition zweier Funktionen wird wohl jeder intuitiv richtig definieren. Prüfen wir nach, kommen wir schnell zum Schluss, dass die Bedingungen für einen Vektorraum der aus Funktionen besteht, erfüllbar sind.

1.2 Eigenschaften von Vektorräumen

1.2.1 Der Untervektorraum (UVR)

Nehmen wir uns einen ”grossen” Vektorraum, mit vielen Elementen, wieR². Die in ihm enthaltenen Vektoren sind von der Form(x, y). Nehmen wir daraus nur die TeilmengeU der Vektoren deren y-Wert gleich 0 ist. Sie sind von der Form(x,0). Ohne nachzuprüfen ist uns klar dass die erlaubten Grundoperationen fürR²auch fürU gelten. Kurz darüber nachgedacht, ist es auch offensichtlich das jede Anwendung der Grundoperationen auf einen Vektor der Form (x,0), nur einen Vektor derselben Form erzeugen kann.

Offensichtlich erfüllt die MengeU alle Kriterien für einen Vektorraum. Gleichzeitig ist U komplett enthalten in R². U ist damit ein Untervektorraum des Vektorraumes R². 1.2.2 Linearkombination

Ein Vektor~bist dann linear abhängig von einer Menge Vektoren A = (a~1, ~a2, . . . , ~an) wenn folgende Gleichung erfüllbar ist ohne dass allec_i gleich 0 sind:

~

a₁c₁+a~₂c₂+. . .+a~_nc_n=~b (1)

~b ist linear abhängig von der Menge A. er lässt sich komplett durch Elemente von A ausdrücken und ist auch definitiv in einem Vektorraum mit der Menge A.

1.2.3 Erzeugungssystem

Sind alle Vektoren~beines VektorraumesV linear abhängig von einer Teilmenge Ades Vektorraumes V, so ist A ein Erzeugungssystem des Vektorraumes V.

(Die triviale LösungA=Vist offensichtlich und sinnlos. Ein Erzeugungssystem macht erst dann Sinn wenn es weniger Elemente hat als der Vektorraum den es erzeugt.) 1.2.4 Basis

Eine Basis eines Vektorraumes V, ist ein Erzeugungssystem für V dessen Elemente alle linear unabhängig voneinander sind. Es hat die minimal nötige Anzahl von Elemen- ten. Daraus folgt auch, dass ein Erzeugungssystem das keine Basis ist, ”überflüssige”

Elemente enthält.

Bemerkung: Ein Erzeugungssystem kann von linear abhängigen Vektoren befreit wer- den, wenn alle Elementea~_i (nach Gleichung 1) durch Linearkombination den Nullvektor erzeugen können. Durch subtrahieren von a~n und dividieren durch cn, zeigt die Glei- chung nun, dass a~_n eine Linearkombination der Vektoren a~₁ bis an−1~ ist. a~_n kann eindeutig erzeugt werden und kann somit aus dem Erzeugungssystem gestrichen wer- den. Kann die Gleichung nicht mehr erfüllt werden ohne, dass alleci = 0sind, so ist aus dem Erzeugungssystem eine Basis geworden (durch Elimination der linear abhängigen Elemente).

Grösse einer Basis (für Vⁿ):

i) Mehr als n Vektoren sind linear abhängig.

ii) Weniger als n Vektoren sind nie ein Erzeugungssystem.

iii) n Vektoren sind dann ein Erzeugungssystem, wenn sie linear unabhängig sind und somit eine Basis bilden.

→ Glaubt man obigen drei Annahmen haben alle Basen für Vⁿ n Elemente.

Auf einen Beweis der obigen Annahmen wird verzichtet. Es sollte aber möglich sein durch Vertiefung der Bedeutung jeder einzelnen Aussage intuitiv deren Richtigkeit zu glauben.

1.3 Normierte Vektorräume

Die Norm eines Vektors wird auch als Länge oder Betrag bezeichnet. Bei der Vorstellung eines Vektors als Pfeil, d.h. als gerichtete Strecke, stellt diese die Länge dar. Beim Lösen von der Idee des Vektors als Pfeil muss eine andere Art gefunden werden, wie der Längenbegriff zu definieren ist. Deshalb werden die Eigenschaften in den Vordergrund gesetzt. Die Norm eines Vektors a wird |a| geschrieben.

Def. 1 Wenn V ein Vektorraum ist und eine Vorschrift einem Vektora ∈Veine reelle Zahl |a| zuordnet, heisst diese Norm, wenn die folgenden Regeln erfüllt sind.

1. i) Für jeden Vektora∈Vgilt|a| ≥0, ii) aus|a|= 0 folgt a= 0.

2. Für jeden Vektor a∈V und für jede Zahl α gilt: |αa|=|α| · |a|

Für komplexe Zahlen: |α|=√

u²+v², falls α=u+iv ist.

3. Für alle Vektoren a, b∈V gilt: |a+b| ≤ |a|+|b| (Dreiecksgleichung).

Die folgenden Normen sind bei Vektorräumen anzuwenden, welche aus Vektoren be- stehen.

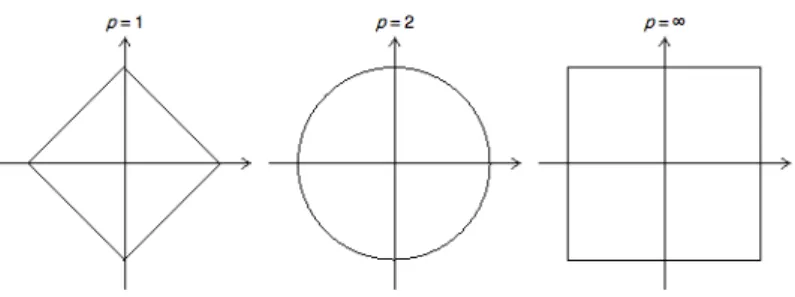
Lp-Normen:|x|p :=|^qp|x1|^p+|x2|^p+|x3|^p| (=Klasse von Normen) Euklidische Norm: |x|₂ :=|^qx₁²+x₂²+x₃²| (gehört zu den L_p-Normen) Maximumnorm:|x|∞ := max(|x₁|,|x₂|,|x₃|)

Abbildung 2: ”Einheitskreisscheibe mit verschiedenen L_p-Normen”

Vektorräume aus Funktionen bestehend benötigen eine andere Norm. Diese Norm |f| ist z.B. der maximale mögliche Wert einer Funktion f(x) ∈ I = [a, b], anstelle von f(x) wird jedoch |f(x)| eingesetzt, da auch die negativen Ausschläge berücksichtigt werden (2). In diese Norm kann auch noch die zweite Ableitung hinein genommen werden (3). Diese Norm kann damit mehr über die Funktion aussagen.

|f|₀ := max

x∈I |f(x)| (2)

|f|₁ := max

x∈I |f(x)|+ max

x∈I |f⁰(x)| (3)

1.4 Skalarprodukt

So wie der Längenbegriff über die Norm definiert werden kann, wird der Begriff des Winkels über das Skalarprodukt definiert.

cosϕ= <a,b>

kak·kbk, falls a6= 0, b6= 0

Wenn (a, b) = 0 stehena und b senkrecht aufeinander, sind sie orthogonal.

Def. 2 Sei V ein reeller Vektorraum. Eine Vorschrift, welche jedem Paar x, y von Vektoren eine reelle Zahl(x, y)zuordnet, heisst Skalarprodukt im VektorraumV, wenn die folgenden Regeln erfüllt sind:

1. Das Skalarprodukt ist linear im zweiten Faktor, d.h. es gilt:

i) (x, y⁽¹⁾+y⁽²⁾) = (x, y⁽¹⁾) + (x, y⁽²⁾) ∀x, y⁽¹⁾, y⁽²⁾ ∈V ii) (x, αy) =α(x, y) ∀x, y ∈V, α∈R

2. Das Skalarprodukt ist symmetrisch, d.h. es gilt:

(x, y) = (y, x) ∀x, y ∈V

3. Das Skalarprodukt ist positiv definit, d.h. es gilt:

i) (x, x)≥0 ∀x, y ∈V;

ii) aus(x, x) = 0 folgt x= 0

Folgend sind Beispiele von Skalarprodukten eines Vektorraums mit Vektoren und an- schliessend Funktionen.

Standardskalarprodukt in Rⁿ: (x, y) := x^Ty

Skalarprodukt in C[a, b] : (f, g) :=^R_a^bf(t)g(t)dt f, g Fkt∈C[a, b]

Def. 3 Zwei Vektoren x, y ∈ V heissen orthogonal, wenn (x, y) = 0. Da cosϕ= 0 falls x6= 0, y 6= 0, wobei ϕ= 90^◦

Satz 1 Sei V ein reeller Vektorraum mit Skalarprodukt.

i) Die orthogonale Projektion eines Vektors x auf den Vektor y 6= 0 ist gegeben durch den Vektor ^(x,y)_(y,y)y

ii) Für alle x, y ∈V gilt:(x, y)² ≤(x, x)(y, y) (Schwarzsche Ungleichung)

iii) Die Vorschrift, die jedemx∈Vdie Zahl |x|:=^q(x, x)zuordnet, ist eine Norm in V.

iv) Stehen zwei Vektorenx, y ∈Vsenkrecht aufeinander, d.h. ist (x, y) = 0, so gilt

|x+y|² =|x−y|² =|x|²+|y|² (Satz von Pythagoras).

Dabei bezeichnet kxk,x∈V die in iii) eingeführte Norm.

2 Lineare Abbildungen

Def. 4 Eine Abbildung F :x ∈V 7→y =F(x)∈ W ist eine lineare Abbildung von V7→W, falls:

i) F(x, y) =F(x) +F(y) ∀x, y ∈V ii) F(αy) =αF(x) ∀α, x∈V

2.1 Lineare Abbildungen und Matrizen

Es giltV =Rⁿ,W=R^mund die lineare AbbildungF :x∈V7→y∈Wist gegeben durch eine m×n-Matrix A, d.h. y=Ax. Sowie Vⁿ bzw V^m für den Vektorraum der n x×1-Matrizen.

Def. 5 SeiF :x∈Vⁿ7→y∈V^m eine lineare Abbildung.

i) Die Menge aller Vektoren, welche auf null abgebildet werden, heisst Kern der Matrix A.

Kern A :={x∈Vⁿ|Ax= 0}

ii) Die Menge aller Bildvektoren y∈V^m heisst Bild der Matrix A.

Bild A:={y∈V^m|Es gibt ein x∈Vⁿ, so dass y=Ax}

Eigenschaften von Kern A und BildA (im Zusammenhang mit Ax=b und Ax= 0) i) b∈BildA7→es gibt einxwomitb =Axlösbar, d.h., dass b∈BildAmindestens

eine Lösung besitzt.

ii) x∈ KernA falls x das homogene Gleichungssystem löst.

iii) Kern A ist ein Unterraum vonVⁿ. Bild A ist ein Unterraum vonV^m.

iv) Es gilt: dim(KernA) +dim(BildA) =n =dimVⁿ da (n−r) +r=n=Vⁿ v) Es gilt: dim(BildA) = (dim(BildA^T)

2.1.1 Zusammensetzen von Abbildungen

H(x) =G(F(x))7→G◦F und liest sich als: ”G verknüpft mit F”

Es gilt: Das Zusammensetzen von linearen Abbildungen ist wiederum linear.

2.2 Abbildungen und Skalarprodukt

Wird der n-dimensionale Vektorraum V zu Rⁿ, dann wird das Skalarprodukt zum Standardskalarprodukt.

Eine lineare Abbildung F ist gegeben durch F : x ∈ Rⁿ 7→ y = Ax ∈ R^m. Das Standardskalarprodukt ist enthalten in Rⁿ und R^m

Es gilt:

i) Die Unterräume Bild A und Kern A^T vonR^m spannen R^m auf:

Bild A+Kern A^T =R^m

ii) die Unterräume BildA und Kern A^T von R^m stehen senkrecht aufeinander:

Aus y∈ Bild A und v ∈ KernA^T folgt (y, v) = 0 iii) dim(BildA) +dim(KernA^T) = dimR^m =m

→ Das Gleichungssystem Ax = b ist genau dann lösbar, wenn b senkrecht auf allen Lösungen des so genannten adjungierten Gleichungssystem A^Ty = 0 steht. Denn aus ii) wissen wir, dass Bild A genau aus denjenigen Vektoren besteht, die senkrecht auf dem Kern von A^T stehen.

Beispiel:Fibonacci-Folge

F₀, F₁, F₂, . . . 7→0,1,1,2,3,5,8, . . .

Die Fibonacci-Folge ist wie folgt definiert:

F₀ = 0, F₁ = 1 F_n+1 =F_n+Fn−1 n= 1,2,3, . . . xⁿ sei F_n

F_n+1

!

, gesucht ist die lineare Abbildungsmatrix A, die xⁿ nach xⁿ⁺¹ über- führt (Alsoxⁿ·A=xⁿ⁺¹)

Lösung:

A= 0 1 1 1

!

7→x³ = 2 3 ·A= 3 5

2.3 Lineare Selbstabbildungen von Vektorräumen

Untersucht werden lineare Abbildungen eines endlichdimensionalen Vektorraumes Vⁿ =Rⁿ. Die linearen Abbildungen sind also quadratische Matrizen.

Def. 6 i) Eine Abbildung F : x ∈ Vⁿ 7→ x⁰ ∈ Vⁿ heisst umkehrbar oder inver- tierbar, falls es zu jedem x⁰ ∈ Vⁿ ein eindeutig bestimmtes x⁰ ∈ Vⁿ gibt mit x⁰ =F(x).

ii) Ist F invertierbar, so heisst die Abbildung, die jedem x⁰ = F(x) das eindeutig bestimmte Urbild x zuordnet, die Umkehrabbildung von F. Diese wird mit F⁻¹ bezeichnet.

Eigenschaften umkehrbarer linearen Abbildungen:

i) Eine lineare AbbildungF :x∈Vⁿ7→x⁰ =Ax∈Vⁿist genau dann umkehrbar, wenn A regulär ist.

ii) Ist F : x 7→ x⁰ = Ax umkehrbar, so ist F⁻¹ linear und F⁻¹ wird durch die Matrix A⁻¹ beschrieben. F⁻¹ :x⁰ 7→x=A⁻¹x⁰.

iii) IstF umkehrbar, so giltF⁻¹◦F =F ◦F⁻¹ =I. Dabei istI die Identität, d.h.

I :x∈Vⁿ 7→x∈Vⁿ.

2.3.1 Koordinatentransformation

Koordinatentransformation = Im Vektorraum wird eine neue Basis gewählt.

Def. 7 Eine Koordinatentransformationist eine umkehrbare lineare AbbildungT :y∈ Wⁿ7→x=T y ∈Vⁿ.

Ein Punktx= (x₁, x₂, . . . , x_n)^T ∈Vⁿ hat mit der Standardbasis des Vektorraums als Komponenten genau die Koordinaten von x.

Nimmt man nun eine neue Basist⁽¹⁾, . . . , t⁽ⁿ⁾∈Vⁿ, kann Punkt xals Linearkombina- tion dieser neuen Vektoren dargestellt werden:

x=y₁t⁽¹⁾+y₂t⁽²⁾+y₃t⁽³⁾+. . .+y_nt⁽ⁿ⁾

yi sind die neuen Koordinaten des Punktes x bezüglich der neuen Basis.

Satz 2 Seien eine lineare Abbildung F : x ∈ Vⁿ 7→ x⁰ = Ax ∈ Vⁿ und eine Koordinatentransformation T :y∈Wⁿ7→x=T y ∈Vⁿ gegeben.

Dann lässt sich die lineare Abbildung in den neuen Koordinaten darstellen als:

G=T⁻¹◦F ◦T :y∈Wⁿ7→y⁰ =T⁻¹AT y ∈Wⁿ

2.3.2 Norm einer Matrix

Die ”Grösse” oder Norm einer Matrix soll angeben, um welchen Faktor sich die Norm eines Vektorsxmaximal verändert, wenn man auf ihn die Abbildung F :x7→x⁰ =Ax anwendet.

Def. 8 Sei A eine n×n-Matrix, und sei in Vⁿ eine Norm kxk∗, x ∈ Vⁿ gegeben.

Dann heisst die Zahl

kAk∗ := sup

x∈Vⁿ,x6=0

(kAxk∗

kxk_∗

)

Norm von A.

Durch Umformen: (∀x∈Vⁿ, x6= 0, der Vektor _kxk¹

∗x hat die Norm 1):

kAk∗ := sup

kxk∗=1

{kAxk∗}

Eigenschaften:

i) kAk∗ ≥0, auskAk∗ = 0 folgt A= 0 ii) kαAk=|α|kAk∗.

iii) kA+Bk∗ ≤ kak∗+kBk∗

iv) kAxk_∗ ≤ kAk_∗kxk_∗ v) kABk∗ ≤ kAk∗kBk∗

2.3.3 Orthogonale Abbildungen Ausgehend von folgenden Annahmen:

Orthonormale Basis ∈V, die Vektorenx ∈V werden mit ihren Koordinatenvektoren identifiziert.

V=Rⁿ ; F :x7→x⁰ =Ax.

Skalarprodukt:(x, y) = x^Ty.

Norm euklidischkxk:=kxk2,x∈Rⁿ

Def. 9 i) Die Abbildung F : x ∈ Rⁿ 7→ x⁰ = Ax ∈ Rⁿ heisst orthogonal, falls (x⁰, y⁰) = (Ax, Ay) = (x, y) ∀x, y ∈Rⁿ gilt.

ii) Die Abbildung F :x∈Rⁿ 7→x⁰ =Ax ∈Rⁿ heisst längentreu, falls kx⁰k=kAxk=kxk ∀x∈Rⁿ gilt.

Eigenschaften: (F :x∈Rⁿ7→x⁰ =Ax∈Rⁿ,(x⁰, y⁰) = (Ax, Ay) = (x, y)) i) F ist orthogonal.

ii) F ist längentreu.

iii) Die Spalten vonA bilden eine orthonormale Basis in Rⁿ.

iv) Die Matrix A ist orthogonal, d.h. es gilt AA^T =I, bzw. A^T =A⁻¹.