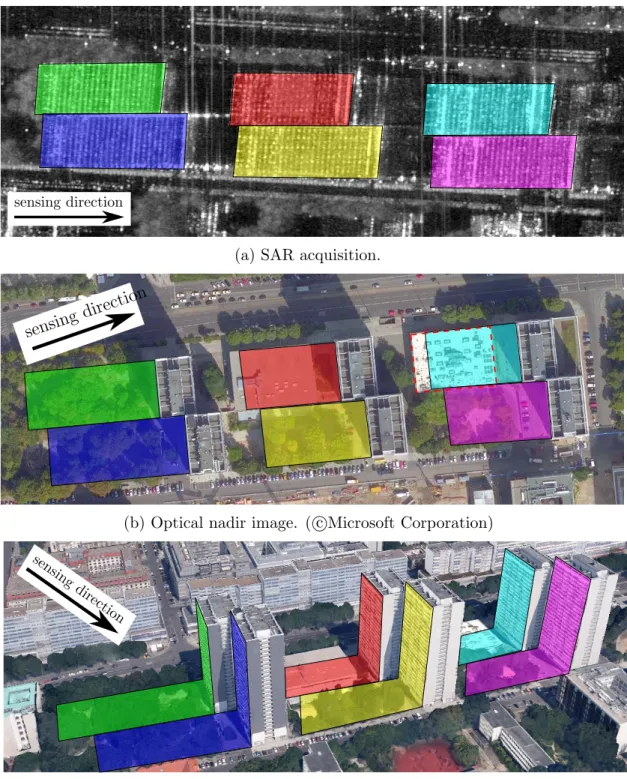
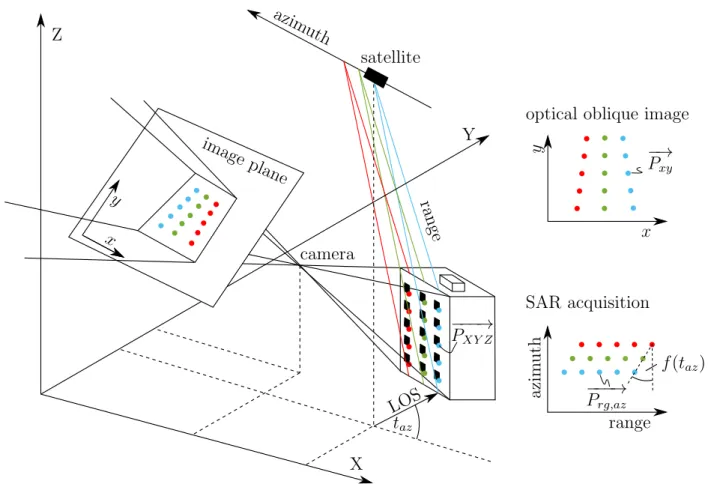
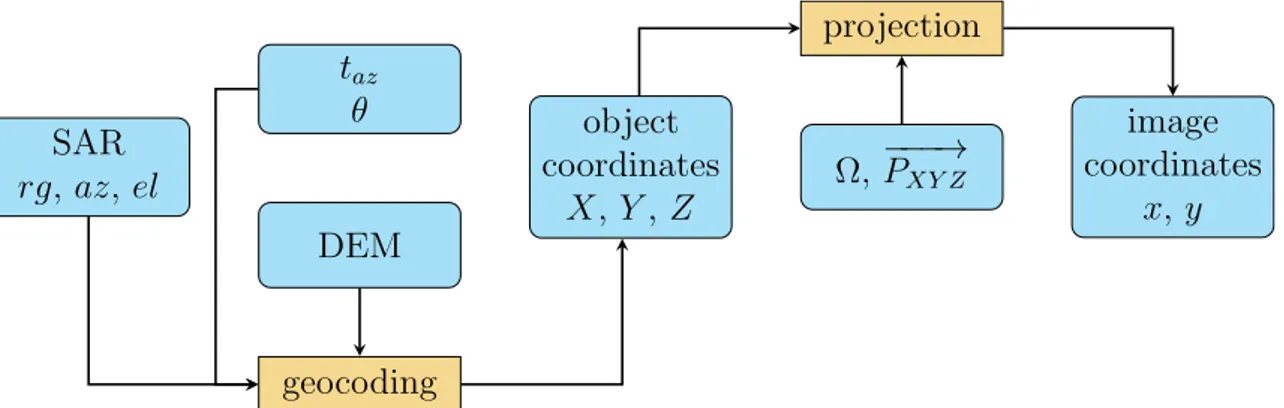
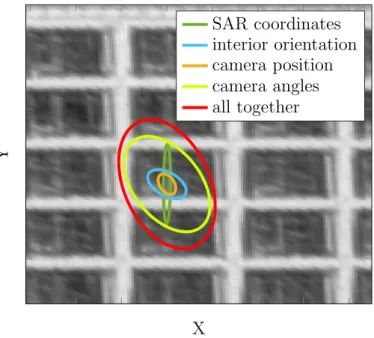
Ausschuss Geodäsi e der Bayer i schen Akademi e der Wi ssenschaf t en
Volltext
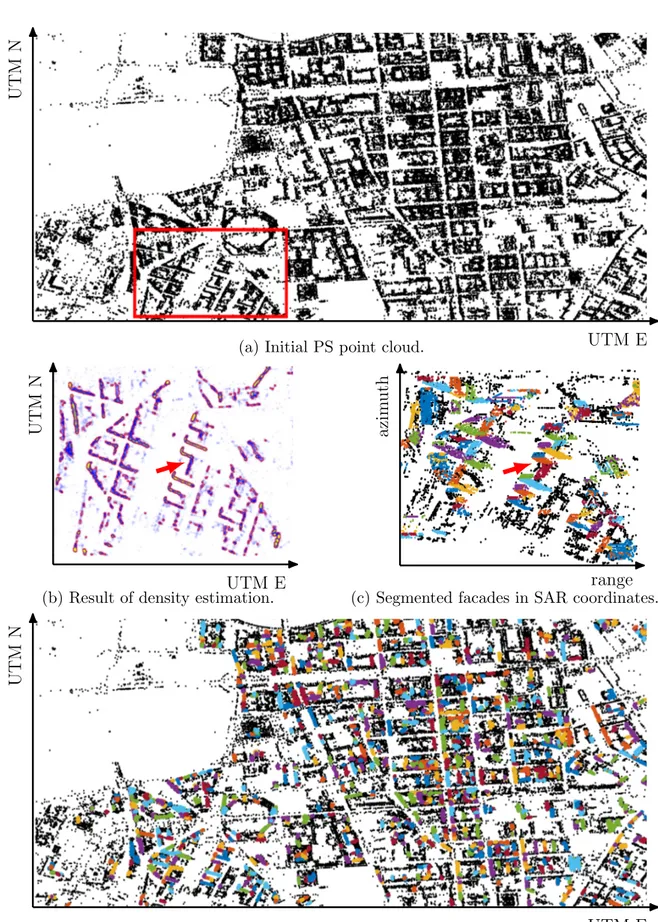
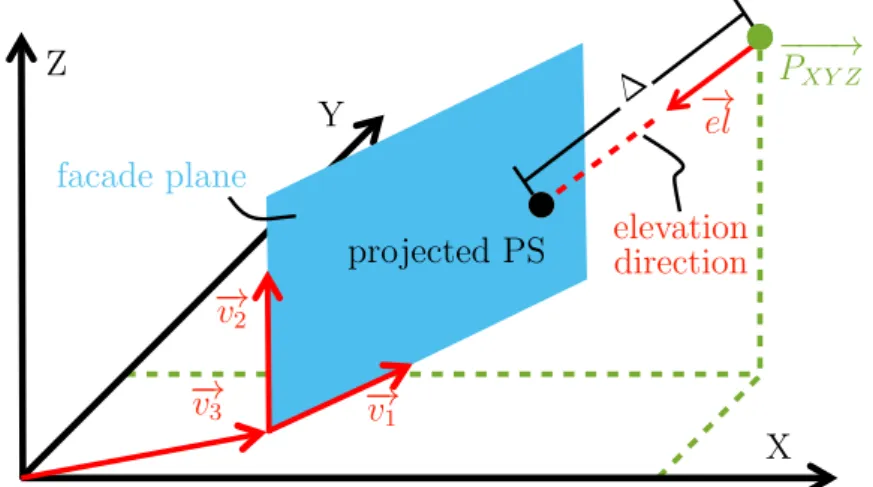
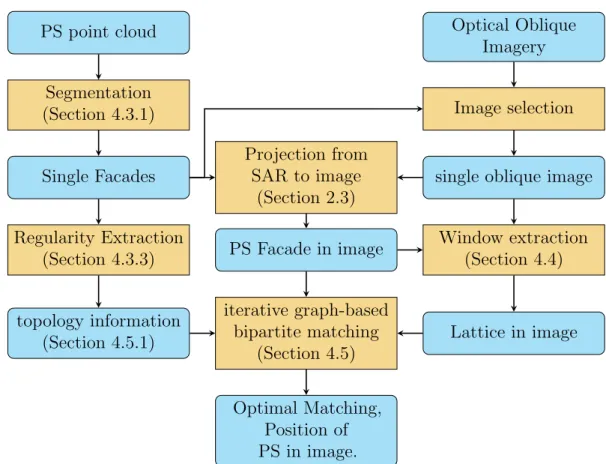
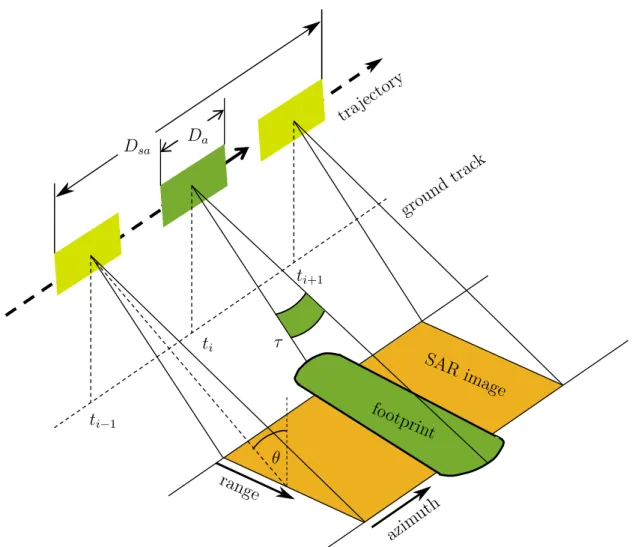
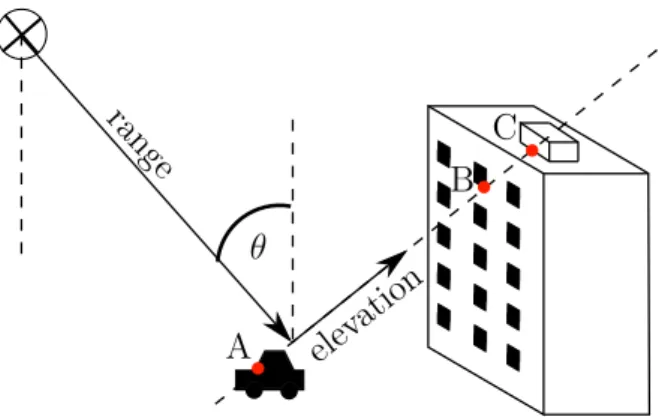
Abbildung

ÄHNLICHE DOKUMENTE
can note that the greater majority of the SMEs are active on a local or on a regio- nal market. This leads us towards a very fundamental point: the SME-population i so
Eine musealisierte Medieninstallation ist aufgrund ihrer historischen Bedeutung oder ihrer kultu- rell-gesellschaftlichen Werte (also ihrer Repräsentativität, Typizität
Shi Yinhong, director of the Center for American Studies at Renmin University, warns in the Financial Times: “When Hu Jintao took over [in 2002] China didn’t need to look to Russia
Having announced the future size of the military presence in Afghanistan two days prior, the president’s re- marks were a symbolic bookend to US engage- ment in the
Player positioning view giving detailed information about a specific player (top shows free kicks and bottom depicts corners).. the arising clusters are grouped by the number and
Heavy precipitation and fl oodwater warnings can be created with radar observations and information from weather models.. This is how, for example, short-term warnings for
termining the most probable feature class for each true positive extracted line (combined for both urban and rural areas) when compared to the reference
When planning the treat- ment allocated to lemmata in e-dictionaries lexicographers should consider the possibility of layering search zones in such a way that the user can