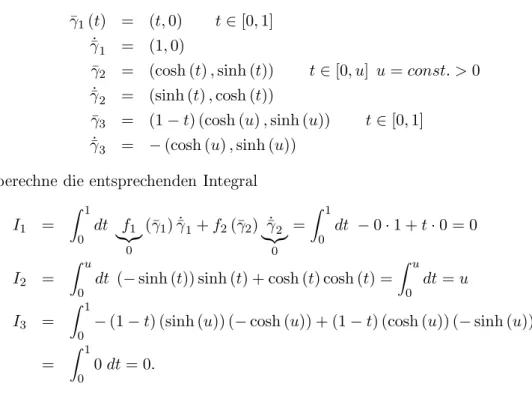3 Übungsblatt Mathematik für Physiker III
3.1 Astroide
Parametrisierung
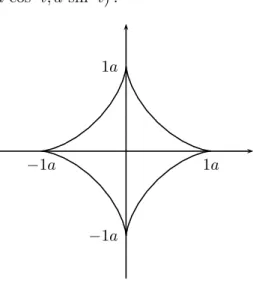
γ ¯ (t) = a cos 3 t, a sin 3 t .
− 1a 1a
1a
− 1a
Abbildung 1:EineAstroide
FüreineUmrundunggibtdieGrenzkurve denUmfangderAstroidean.FürdieLänge
der Kurve bei einer Umrundung, wobei wir auf Grund der Symmetrie nur den ersten
Quadranten betrachten unddanach mit 4multiplizieren können,folgt:
L (¯ γ (t)) = Z
¯ γ
1 ds = 4 · Z π
2
0
s d
dt a cos 3 t 2
+ d
dt a sin 3 t 2
dt,
= 4 · Z π
2
0
q
( − 3a cos 2 t sin t) 2 + 3a sin 2 t cos t 2 dt,
= 4 · Z π
2
0
3a cos t sin t q
cos 2 t + sin 2 t
| {z }
=1
dt,
= 4 ·
− 3 2
a cos 2 t |
π
0 2 = 4 · 3 2 a,
= 6a.
Somit folgt für denUmfang derAstroide
U = 6a.
1e 2e
− 1e
− 2e
− 3e
1e 2e
− 1e
− 2e
− 3e
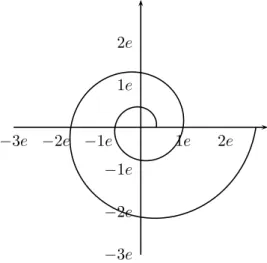
Abbildung 2:Die logarithmische Spirale
(b)
Fürdie Länge derKurve gilt:
L (¯ γ ) = Z b
a
s d
dt e ct cos t 2
+ d
dt e ct sin t 2
dt,
= Z b
a
q
(c e ct cos t − e ct sin t) 2 + (c e ct sin t + e ct cos t) 2 dt,
= Z b
a
q
c 2 e 2 ct cos 2 t − 2c e 2 ct cos t sin t + e 2 ct sin 2 t + c 2 e 2 ct sin 2 t + 2c e 2 ct cos t sin t + e 2 ct cos 2 tdt,
= Z b
a
e ct q
(c 2 + 1)dt,
=
p (c 2 + 1) c e ct | b a ,
= r
1 + 1 c 2
e cb − e ca .
Bei demFall:
a → −∞ ,
verschwindet diezweite Exponentialfunktion undesbleibt:L (¯ γ (t)) = r
1 + 1
c 2 e cb .
DamitsichdiebeidenKurven schneiden,müssen andemSchnittpunkt dieNormen,also
der Abstand vom Ursprung, gleich sein. Aufgrund der Bijektivität, das heiÿt Monoto-
nieund Surjektivität derExponentialfunktion ist dashöchstens undmindestens einmal
gegeben. Aufgrund der Winkelinvarianz der Kreiskurve, muss auschlieÿlich die Norm
betrachtet werden.
Um den Schnittwinkel
α
der zwei Kurvenγ ¯
und¯ γ k zu bestimmen benutzt man die
Formel:
cos (α) = h γ, ˙¯ γ ˙¯ k i
|| γ ˙¯ || || γ ˙¯ k ||
¯
γ (t) ˙ = r cos (t) r sin (t)
!
˙¯
γ (t) ˙ = − r sin (t) r cos (t)
!
¯
γ k (t) ˙ = e ct cos (t) e ct sin (t)
!
˙¯
γ k (t) ˙ = ce ct cos (t) − e ct sin (t) ce ct sin (t) + e ct cos (t)
!
Daraus kannmandie Normen berechnen:
|| γ ˙¯ (t) || = q r 2 sin 2 (t) + r 2 cos 2 (t) = r
|| γ ˙¯ k (t) || 2 = ce ct cos (t) − e ct sin (t) 2 + ce ct cos (t) − e ct sin (t) 2
= e 2 ct 1 + c 2
...unddasSkalarprodukt...
h γ, ˙¯ γ ˙¯ k i = ˙
* ce ct cos (t) − e ct sin (t) ce ct sin (t) + e ct cos (t)
!
, − r sin (t) r cos (t)
!+
= − rce ct sin (t) cos (t) + re ct sin 2 (t) + rce ct sin (t) cos (t) + re ct cos 2 (t)
= re ct .
Daraus folgt:
cos (α) = re ct r p e 2 ct (1 + c 2 )
= 1
√ .
Vektorfeld:
f ~ (x, y, z) :=
− cx
− cy
− cz
,
Bewegung durch diese Kraftfeldvon
¯ a = (1, 0, 0)
nach¯ b = (1, 0, 1) .
(a)
FürdieStreckewählenwirdieParametrisierung
¯ γ 1 = (0, 0, t)
mitdemIntervallt ∈ [0, 1] : Z
γ ¯
D f ~ (~ x) , d~ x E = Z 1
0
D f ~ (¯ γ (t)) , γ ˙¯ (t) E dt = Z
γ ¯
( − c z dz) = − c Z 1
0
s t d
dt t 2
dt = − c Z 1
0
t dt = − c 2 .
(b)
FürdieSchraubenliniewählenwirdieParametrisierung
γ ¯ 2 = (r cos t, r sin t, 2 t π )
mitdemIntervall
t ∈ [0, 2π] : Z
γ ¯
D f ~ (~ x) , d~ x E = Z 2 π
0
D f ~ (¯ γ (t)) , γ ˙¯ (t) E dt = Z
¯ γ
( − c) (x dx + y dy + z dz)
= − c Z 2 π
0 − r 2 cos t sin t + r 2 sin t cos t + 1
2π 2
t
!
dt = − c 1
2π
2 Z 2 π 0
t dt
= − c 1
2π 2 1
2 t 2 | 2 0 π = − 2cπ 2 1
4π 2 = − c 2 .
Die Bewegungen verbrauchen beide gleich viel Energie, da das Kraftfeld konservativ
ist.
3.4 2D-Vektorfeld
Vektorfeld:
f ~ (x, y) = − y x
! .
Es gilt klassisch
R
γ ¯ − y dx + x dy.
Die Kurve
γ ¯ a kannmanfolgendermaÿen parametrisieren:
¯
γ a (t) = (1 − t) (a, b) + t (c, d) t ∈ [0, 1]
˙¯
γ a (t) = (c − a, d − b) .
Daraus folgt
Z 1 0
dt (bt − b − td) (c − a) + (a − at + ct) (d − b)
= Z 1
0
dt ab − bc + ad − ab + t (bc − ab − cd + ad − ad + ad + cd − bc)
= ad − bc
(b)
Die Kurve
γ ¯ b kann manfolgendermaÿen parametrisieren:
¯
γ b 1 (t) = t 0
!
t ∈ [0, 1]
˙¯
γ b 1 (t) = 1 0
!
¯
γ b 2 (t) = cos (t) sin (t)
!
t ∈ [0, ϕ]
˙¯
γ b 2 (t) = − sin (t) cos (t)
!
¯
γ b 3 (t) = (1 − t) cos (ϕ) sin (ϕ)
!
t ∈ [0, 1]
˙¯
γ b 3 (t) = − cos (ϕ)
− sin (ϕ)
! .
Daraus ergeben sich die folgenden 3 bestimmen Integrale, in die man die Gesamtkurve
zerlegenkann:
I 1 = Z 1
0
( − 0) · 1 + t · 0 dt = 0 I 2 =
Z ϕ
0 − sin (t) ( − sin (t)) + cos (t) cos (t) dt = ϕ I =
Z 1
− (1 − t) sin (ϕ) ( − cos (ϕ)) + (1 − t) cos (ϕ) ( − sin (ϕ)) dt = 0
Manzerteile dasKurvenintegralwieder in3Teile:
¯
γ 1 (t) = (t, 0) t ∈ [0, 1]
˙¯
γ 1 = (1, 0)
¯
γ 2 = (cosh (t) , sinh (t)) t ∈ [0, u] u = const. > 0
˙¯
γ 2 = (sinh (t) , cosh (t))
¯
γ 3 = (1 − t) (cosh (u) , sinh (u)) t ∈ [0, 1]
˙¯
γ 3 = − (cosh (u) , sinh (u))
und berechne dieentsprechenden Integral
I 1 = Z 1
0
dt f 1
|{z}
0
(¯ γ 1 ) ˙¯ γ 1 + f 2 (¯ γ 2 ) ˙¯ γ 2
|{z}
0
= Z 1
0
dt − 0 · 1 + t · 0 = 0
I 2 = Z u
0
dt ( − sinh (t)) sinh (t) + cosh (t) cosh (t) = Z u
0
dt = u I 3 =
Z 1
0 − (1 − t) (sinh (u)) ( − cosh (u)) + (1 − t) (cosh (u)) ( − sinh (u))
= Z 1
0
0 dt = 0.
Daher lautet dasIntegralumdasgesamte 'Dreieck' herum:
I 1 + I 2 + I 3 = u.
Der Integrationsweg wirddurch folgendeSkizze ersichtlich:
1 2
1
− 1
x y
u = 1
Abbildung 3:DasDreieck