in or
Volltext
Abbildung
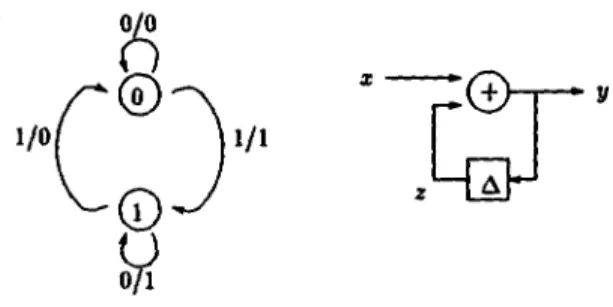



ÄHNLICHE DOKUMENTE
The accepted objectives of formal techniques are notably dierent from the requirements of the fault injection process. Thus, our formal methods approach towards V&V and FI
In this paper we have extended the threat model for human identification protocols by assuming a stronger attacker who can predict random decisions made by the human. We have stated
Moreover, having better information about borrowers has implications within lender groups: formal lenders rely less on collateral with longer borrower-relationship and
Other objectives include verification of the correlations with an experiment, recommended procedure to use empirical correlations in field and investigation of how
For a research paper, this involves deter- mining if the work presented is correct, if the problem studied and the results obtained are new and significant, if the quality of
Soon it was discovered that elements at low concentrations could be used to determine the nature of the ore from which the metal was smelted and possibly the geographical origin
Response times (lines) and error rates (bars) of the ‘same’- responses in Experiment 1: Categorizations at different levels of abstrac- tion (basic level, subordinate level, and
The idea that philosophy should proceed for- mally ("more geometrico". as in the title of Spinoza's Ethica) has been around for some time, hut both the auilude





