Matthias BRANDL, Erlangen-Nürnberg, Swetlana NORDHEIMER, Berlin
Zufällig vernetzt? Vernetzungen mit Stochastik im Lehrplan und darüber hinaus
Spätestens seit PISA gilt das Vernetzen verschiedener mathematischer As- pekte und Teilgebiete in der Schule als eine bedeutende und typische Ei- genschaft von Mathematik bzw. mathematischem Denken weltweit.
Nichtsdestotrotz stellt dies eine Herausforderung für Theorie und Praxis des Unterrichts dar. In diesem Beitrag sollen einerseits Möglichkeiten einer theoretischen Einordnung, andererseits konkrete Beispiele skizziert wer- den.
1. „Verstehens-Shift“ durch Vernetzung
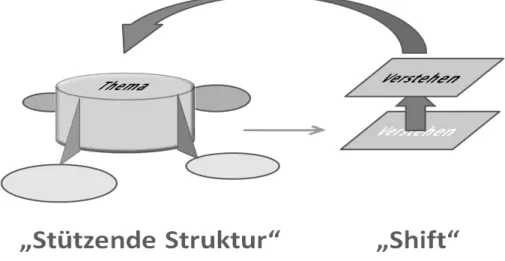
Lietzmann, Wittenberg, Wagenschein, Vollrath, Wittmann und andere ver- gleichen Mathematik metaphorisch mit einem Netz und zeigen an konkre- ten Beispielen, wie vor allem Geometrie, Arithmetik und Algebra im Un- terricht miteinander verknüpft werden können. Ausgehend von diesen An- sätzen illustriert Abb. 1 unser Verständnis von so genannter Vernetzung:
Abb. 1: Verstehens-Shift durch Vernetzung eines Themas
Durch die Vernetzung eines bestimmten Themas mit benachbarten mathe- matischen Teilgebieten findet auf der Ebene des Verstehens ein „Shift“
statt, der es den Lernenden ermöglicht, das Thema sozusagen von einer hö- heren Warte aus besser zu verstehen. Im fortgeführten Lernprozess werden die Nachbargebiete zwar „verblassen“, doch sie bleiben weiterhin eine stützende Struktur für das zentrale Themengebiet. In diesem Sinne sehen wir in der „Vernetzung“ eine Möglichkeit zwischen den aktuellen Heraus- forderungen der schulischen Praxis und den Ideen von Wagenschein („Einwurzelung“) und Bruner („scaffolding“) zu vermitteln (siehe Wagen- schein, 1968; Bruner, 1976).
2. Vernetzungen in den Rahmenlehrplänen
In den Lehrplänen deutscher Bundesländer finden sich verschiedene Auf- fassungen von Vernetzungen. Demnach kommt Vernetzung als eine der fünf Leitideen im Bildungsplan für Gymnasien in Baden-Württemberg vor.
In Sachsen wird für die Gymnasien am Ende jedes Schuljahres ein Lernbe- reich „Vernetzung“ mit einer bestimmten Pflichtstundenzahl vorgeschrie- ben. Dabei sollen beispielsweise die sächsischen Gymnasiasten am Ende der Klasse 6 im Rahmen des Lernbereichs „Anteile“ Bruchrechnung, Sto- chastik und Geometrie wiederholen und vernetzen. In den gymnasialen Lehrplänen für Bremen und Mecklenburg-Vorpommern wird Vernetzen als Teilkompetenz der prozessbezogenen Kompetenz Argumentieren gesehen.
Im Rahmenlehrplan des Saarlands werden inhaltliche Hinweise auf die Vernetzungen für Gymnasien gegeben. In Bayern finden Gymnasiallehrer das Wort „Vernetzung“ nicht so häufig in den Rahmenlehrplänen. Dafür werden dort Aufgabenbeispiele angeboten, die verschiedene Themenberei- che mit einbeziehen.
Zwar wird Vernetzung häufig eher in den gymnasialen Lehrplänen explizit thematisiert, man findet dieses Prinzip aber auch in einigen Lehrplänen für die anderen Schularten. So gilt beispielsweise in Hessen Vernetzung als ei- nes der Ziele des Mathematikunterrichts in der Hauptschule. In Berlin, Brandenburg, Hamburg, Rheinland-Pfalz werden mögliche fachinhaltliche Vernetzungen zwischen den Themenbereichen und Leitideen genannt. Die ausgewiesenen Vernetzungen verbinden häufig algebraische und geometri- sche Themen. Ein klassisches Beispiel dafür ist die Trigonometrie. Veran- schaulichung von Brüchen und Wahrscheinlichkeiten, Kreisdiagramme sind weitere Beispiele für häufig empfohlene Vernetzungen. Für die Klas- sen 5/6 werden in Berlin und Brandenburg sogar verbindliche innermathe- matische Verknüpfungen vorgeschrieben.
Was unter Vernetzung jeweils konkret verstanden wird, ist selten explizit beschrieben und erschließt sich nur mit Hilfe von Beispielen. Der Konkre- tisierungsgrad dieser variiert von der Angabe von Themenüberschriften bis hin zu konkreten Aufgaben. Dabei wird aber z.B. das reichhaltige Potenzial für die Vernetzung von Inhalten aus der Stochastik mit anderen Inhalten bei weitem nicht ausgeschöpft (siehe Engel 2007).
3. Beispiel: Pythagoras-Bäume zu den Zufallsexperimenten
In Analogie zur Veranschaulichung von arithmetischen Konzepten (z.B.
Brüchen) bzw. algebraischen Konzepten (z.B. Termen), kann auch nach ei- ner geometrischen Veranschaulichung von Wahrscheinlichkeiten bzw. rela-
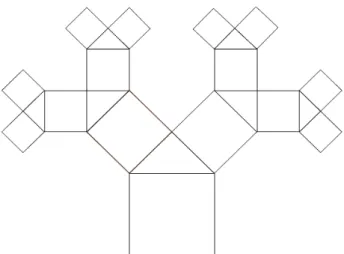
tiven Häufigkeiten gesucht werden. So können beispielsweise Pythagoras- Bäume als Alternative zu Baumdiagrammen mögliche Ausgänge eines mehrstufigen Zufallsexperiments darstellen.
Abb. 2: Symmetrischer Pythagoras-Baum
In Abbildung 2 wird ein dreimaliger Münzwurf mit einem Pythagoras- Baum veranschaulicht. Die dem zeitlichen Ablauf entsprechende Leserich- tung ist von unten nach oben. Für die Darstellung eines Versuchs in den höheren Stufen steht wie am Anfang ein Quadrat zur Verfügung. Mit jeder Stufe halbiert sich der Flächeninhalt der entstehenden Quadrate. Die Sum- me der Flächeninhalte der Quadrate bleibt innerhalb einer Stufe gleich.
Wird ein Spielwürfel viermal hintereinander geworfen und gefragt, wie oft die Zahl sechs vorkommt, so kann das Experiment nicht mehr mit einem symmetrischen Pythagoras-Baum dargestellt werden. Wie würde der Py- thagoras-Baum aussehen, der zu diesem Experiment passen würde? Schüler der Mathematischen Schülergesellschaft der HU-Berlin haben das gleich- schenklig rechtwinklige Dreieck mit einem nicht-gleichschenklig recht- winkligen Dreieck ersetzt. Dadurch sind in der zweiten Stufe zwei Quadra- te entstanden, deren Flächeninhalte im Verhältnis 1:5 standen. Somit haben sie das Modell mit Hilfe von Thaleskreis und Pythagoras auf andere Ber- noulli-Experimente übertragen.
4. Beispiel: Bestimmung von Pi
Ausgangspunkt einer stochastischen Bestimmung von Pi ist ein Quadrat der Seitenlänge a mit einbeschriebenem Kreis. Auf dieses Quadrat fallen zufäl- lig n Regentropfen. Mit welcher Wahrscheinlichkeit treffen diese in den Kreis? Die Kombination zweier unterschiedlicher Betrachtungsweisen sei- tens der Geometrie und der Stochastik liefert einen Näherungswert für Pi:
π ≈ 4⋅ (Zahl der Tropfen, die in den Kreis fallen / n)
Dies kann nun mittels eines Tabellenkalkulationsprogramms berechnet werden. Hilfreich hierfür ist die Ausnutzung der Symmetrie, indem nur ein Viertelkreis betrachtet wird, dessen Mittelpunkt im Ursprung liegt. Radius 1 ermöglicht die direkte Verwendung von Zufalls zahlen in MS Excel; die Entscheidungsregel ergibt sich aus dem Satz des Pythagoras: x2 + y2 ≤ 1.
Detailliertere und weiterführende Hinweise zur praktischen Durchführung im Unterricht finden sich z. B. in Müller (2006).
5. Beispiel: Vom Lotto zum Pascalschen Dreieck
In Brandl (2011) geht es um die Ausgangsfrage: „Steigt die Wahrschein- lichkeit, dass ich meinen Jackpot-Gewinn teilen muss mit der Anzahl der Teilnehmer?“ Die Antwort lautet zunächst: Ja, natürlich. Aber: Wie genau hängt diese Tatsache von der Zahl n der Teilnehmer ab?
Zunächst ergibt sich hier als mathematisches Modell für die zu erwartende Wahrscheinlichkeit eine Kombination aus hypergeometrischer und Bino- mialverteilung. Unter dem analytischen Blickwinkel funktionaler Abhän- gigkeiten ergibt sich sodann die Antwort aus einer Kurvendiskussion.
Im weiteren Verlauf der Lerneinheit wird die Ausgangsfrage verallgemei- nert: „Wie verändert sich die Wahrscheinlichkeit, dass sich k Teilnehmer bei steigender Teilnehmerzahl n einen Jackpot teilen müssen?“ Hier kommt nun der Binomialkoeffizient mit ins Spiel. Auch dieser wird nun unter funktionalen Gesichtspunkten betrachtet, als Polynom vom k. Grad in n in- terpretiert, und anhand des Pascalschen Dreiecks, iterativen Folgen und Dreieckszahlen illustriert. Das Thema sorgt damit für eine fachinhaltliche Vernetzung von Stochastik, Analysis, Algebra und Geometrie.
Literatur
Brandl, M. (2011): Der Lotto-Jackpot in der (Kurven-)Diskussion – eine vernetzende Unterrichtseinheit für den Stochastik- und Analysisunterricht der Oberstufe, in A.
Brinkmann, J. Maaß, H.-S. Siller (Hrsg.): Mathe vernetzt - Anregungen und Materia- lien für einen vernetzenden Mathematikunterricht. Schriftenreihe des Arbeitskreises
"Vernetzungen im Mathematikunterricht" der GDM, Band 1. Köln: Aulis Verlag, S.
99 – 108.
Bruner, J.S.; Ross, G.; Wood, D. (1976): The role of tutoring and problem solving, in:
Journal of Child Psychology and Psychiatry.
Engel, J. (2007): Daten, Funktionen, Zufall, Modelle: Vernetzung von Leitideen des Mathematikunterrichts. Beiträge zum Mathematikunterricht, S. 4 - 13.
Müller, J. H. (2006): Reis im Kreis, in mathematik lehren, 138, S. 23 - 43.
Wagenschein, M. (1968): Verstehen lehren. Genetisch - Sokratisch – Exemplarisch.
Weinheim, Basel: Beltz.