Quantum Computing
Prof. Dr. Christoph Lehner
Lecture for Summer of 2020
Contents
1 Ideal quantum computing 5
1.1 Introduction to digital quantum computing . . . 5
1.1.1 Qubits, gates, measurements . . . 5
1.1.2 Common one-qubit gates . . . 6
1.1.3 Common two-qubit gates . . . 7
1.1.4 Quantum circuits . . . 8
1.1.5 Example: Bell states . . . 9
1.1.6 Quantum simulator . . . 10
1.1.7 Many-qubit gates . . . 10
1.1.8 Quantum parallelism . . . 12
1.2 Quantum algorithms . . . 13
1.2.1 Deutsch–Jozsa algorithm . . . 13
1.2.2 Grover algorithm . . . 16
1.2.3 Parenthesis: Arithmetic gates, ancilla and garbage qubits, uncomputing . . . 18
1.2.4 Example: Solving an equation using Grover’s algorithm . 23 1.2.5 The quantum Fourier transform . . . 34
1.2.6 Example: Addition through Fourier transform . . . 36
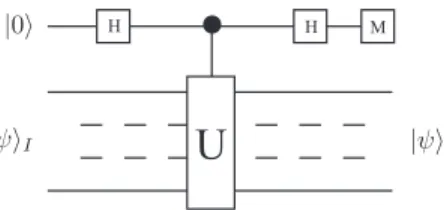
1.2.7 Phase estimation . . . 38
1.2.8 Example: Order-finding . . . 46
1.2.9 Application: Shor’s algorithm . . . 61
1.2.10 Parenthesis: RSA encryption . . . 65
2 Real quantum computing 69 2.1 Real quantum hardware . . . 69
2.1.1 Characteristics of real quantum computers . . . 69
2.1.2 Survery of universal digital quantum computers (2020) . . 72
2.1.3 Example of hardware implementation: IBM 5 qubit systems 74 2.2 Formal treatment of quantum noise . . . 77
2.2.1 Principal system and environment . . . 77
2.2.2 Mixed states, density matrix, and quantum operations . . 78
2.2.3 Noise channels . . . 81
2.2.4 Fidelity and trace distance . . . 83
2.2.5 Simulating quantum noise . . . 84 3
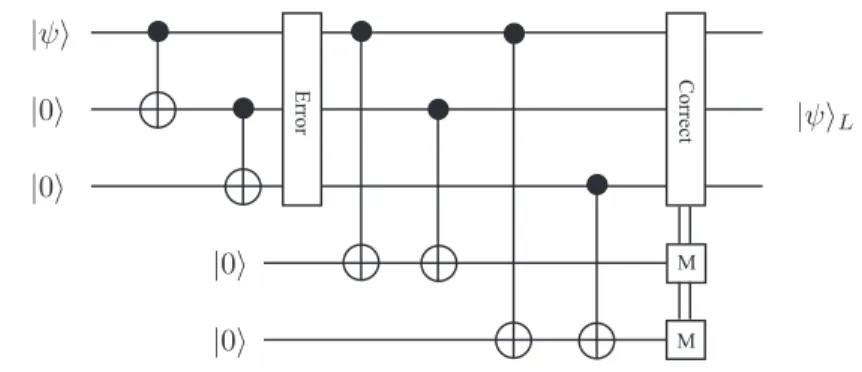
2.3 Quantum Error Correction . . . 95
2.3.1 The three-qubit bit flip code . . . 95
2.3.2 The three-qubit phase flip code . . . 100
2.3.3 The Shor code . . . 103
2.3.4 Stabilizer formalism . . . 107
2.3.5 Gottesman Knill Theorem . . . 112
2.3.6 Fault tolerance – general idea . . . 114
2.3.7 Threshold theorem . . . 115
2.3.8 Fault tolerant operations . . . 116
3 Scientific quantum computing 119 3.1 One-dimensional spin-chain . . . 119
3.2 One-dimensional free particle . . . 130
3.3 One-dimensional particle in time-independent potential . . . 137
3.4 One-dimensional real scalar quantum field theory . . . 144
Chapter 1
Ideal quantum computing
1.1 Introduction to digital quantum computing
1.1.1 Qubits, gates, measurements
• A single qubit is a vector of unit length in the two-dimensional complex vector spaceS spanned by
|0i= 1
0
, |1i=
0 1
. (1.1)
• The direct product ofN vector spacesS creates the vector space SN SN ≡
ON i=1
S (1.2)
with dimensionality 2N. A state ofN qubits is represented by a vector of unit length inSN.
• Example: A two-qubit vector space is spanned by
|00i=
1 0 0 0
, |01i=
0 1 0 0
, |10i=
0 0 1 0
, |11i=
0 0 0 1
. (1.3)
• In general, thei-th component of a basis vector ofSN will be written as (|bN−1bN−2· · ·b0i)i=
(1 fori=PN−1 j=0 bj2j,
0 else (1.4)
with 0≤i <2N. From left-to-right we therefore write the most-significant to least-significant bits. On occasion, we will write|iifor|bN−1bN−2· · ·b0i withi=PN−1
j=0 bj2j and use the function bitj(i) =bj. 5
• A quantum gate is a unitary matrix acting onSN.
• For a general state
|Ψi=
2XN−1 i=0
Ψi|ii (1.5)
with Ψi∈CandP2N−1
i=0 |Ψi|2= 1 we define Pj(|Ψi) =
2XN−1 i=0;bitj(i)=1
|Ψi|2 (1.6)
and a probabilistic measurement operation Mj :SN →SN ⊗ {0,1} that with likelihoodPj(|Ψi) maps|Ψito
2XN−1 i=0;bitj(i)=1
Ψi
pPj(|Ψi)|ii ⊗1 (1.7) or else to
2XN−1 i=0;bitj(i)=0
Ψi
p1−Pj(|Ψi)|ii ⊗0. (1.8) This operation therefore maps a qubit to a qubit and a classical bit in a probabilistic manner.
• The classical bit returned byMj is insensitive to a global complex phase of the state. This is important since the classical bits are the only way to extract information from the system. Global phases are therefore not important.
• A set of quantum gates that when combined can generate an arbitrary unitary matrix up to an arbitrary global phase is calleduniversal.
• A digital quantum computer is a machine that can apply quantum gates on N-qubit states and perform such measurements that provide a mapping to classical bits. Such a machine is called universal if it can apply a universal set of quantum gates.
1.1.2 Common one-qubit gates
• Hadamard
H = 1
√2
1 1 1 −1
(1.9) Action: |0i → √12(|0i+|1i),|1i → √12(|0i − |1i)
1.1. INTRODUCTION TO DIGITAL QUANTUM COMPUTING 7
• Phase shift gate
Rφ= 1 0
0 eiφ
. (1.10)
Action: |0i → |0i,|1i →eiφ|1i
• Pauli-X or NOT gate
X = NOT = 0 1
1 0
(1.11) Action: |0i → |1i,|1i → |0i
• Pauli-Y
Y =
0 −i i 0
(1.12) Action: |0i →i|1i,|1i → −i|0i
• Pauli-Z
Z= 1 0
0 −1
=Rπ (1.13)
• T =Rπ/4,S=Rπ/2
1.1.3 Common two-qubit gates
• Swap
SWAP =
1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1
(1.14)
Action: |00i → |00i,|01i → |10i,|10i → |01i, |11i → |11i
• CNOT
CNOT =cX=
1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0
(1.15)
Action: |00i → |00i,|01i → |01i,|10i → |11i, |11i → |10i;
Here: least-significant bit is target bit, most-significant bit is control bit Version for switched target and control bits in exercises.
1.1.4 Quantum circuits
• A quantum circuit is a specific combination of gates and measurements.
We introduce a graphical representation.
• A qubit is represented by a single line
|ψi
• N qubits may be grouped and written as
|ψi N
• A classical bit is represented by a double line bi
• The measurement of a qubit is represented as
|ψi bi
• A one-qubit gate operation is represented as
|ψi H
for the Hadamard gate and analog for other gates.
• The NOT gate has the special representation
|ψi
• Gate applications are read from left to right, so
|ψi A B
is represented as
BA|ψi (1.16)
in matrix notation.
• CNOT with least-significant target bit is represented as
1.1. INTRODUCTION TO DIGITAL QUANTUM COMPUTING 9
|ψtargeti
|ψcontroli
One typically writes the least-significant qubit at the top. The case with least-significant control bit will be discussed in the exercises.
• A general controlled one-qubitU operation is represented as
|ψcontroli
|ψtargeti U
where U could, e.g., be H or Rφ, which is only applied to target bit if control bit is 1.
• SWAP is represented as
|ψi
|φi
1.1.5 Example: Bell states
The circuit
|0i H b0
|0i b1
performs the Bell experiment. After the Hadamard the system is in state
√1
2(|00i+|01i) (1.17)
and then after the CNOT in
√1
2(|00i+|11i). (1.18) The four possible classical results then are measured with probability
P(00) =P(11) = 1
2, P(10) =P(01) = 0. (1.19) The bits are maximally correlated and we always findb0=b1. Such correlation between qubits is called entanglement and is at the core of many quantum algorithms.
1.1.6 Quantum simulator
• A digital quantum computer can be simulated on a classical computer.
• On the course webpage, there is a link to http://github.com/lehner/sqc, a simple Python implementation of such a simulator; In this week’s ex- ercises, we will discuss the usage of this library and we will use it to implement some of the algorithms introduced in the lecture.
• Caveat: with increasing number of qubits N, the problem size for the classical simulation increases as 2N.
1.1.7 Many-qubit gates
• It is useful to define
√X =HRπ/2H =1 2
1 +i 1−i 1−i 1 +i
(1.20) with√
X√
X =X =NOT.
• Extend the CNOT gate by another control gate to the C2NOT or Toffoli gate. It can be implemented as
=
√X √
X† √
X
• For controlled-U gate, replace √
X by √
U; see also problem set 2. For this, we will need
X1/n=HRπ/nH . (1.21)
• Similarly the CnNOT can be obtained from the Cn−1NOT gate. For C3NOT
=
√X √
X† √
X
With worker bits, we can implement this more efficiently, see problem set 2.
1.1. INTRODUCTION TO DIGITAL QUANTUM COMPUTING 11
• We can also trigger on a 0 bit value by adding additional NOT gates. We write this with an empty circle
= X X
• Now we are ready to find a representation of a gate s(ij) on SN with s(ij)|ii=|ji, s(ij)|ji =|ii, s(ij)|li=|li for 0≤i, j, l < 2N and l 6=i, j.
This matrix plays a crucial role in the proof of universality done in the exercises
• Consider the bit-wise representation of i and j. Let i and j differ in n bits, then we can define so-called Gray codes gm, where g0 =i, gn =j, andgmandgm−1 only differ in one bit.
Example: i = 3 (011), j = 4 (100); g0 = 3 (011), g1 = 7 (111), g2 = 5 (101),g3= 4 (100)
• We can implements(gm,gm−1)by the CN−1NOT gate with target bit being the differing bit and triggering on the values of the common bits.
Example: g2= 5 andg3= 4 from above
3 3
s(54) =
• Then
s(ij)=s(g1,g0)· · ·s(gn−1,gn−2)s(gn,gn−1)· · ·s(g1,g0) (1.22) Example: i= 3,j= 4
3 3
s(34) =
1.1.8 Quantum parallelism
• For a general function
f :{0,1}N → {0,1} (1.23) it will be useful to define
Uf :SN ⊗S→SN ⊗S,|xi ⊗ |yi 7→ |xi ⊗ |y⊕f(x)i, (1.24) where ⊕here means the modulo 2 operation. Such a function effectively evaluatesf for all possible values in parallel. We will also write|xi⊗|yi=
|x, yi. Note that the action on a general element ofSN ⊗S is defined by the action on each basis element|x, yi.
• Since we cannot implement a non-reversible gate operation (quantum gates are unitary), we cannot map simply to|xi ⊗ |f(x)i. The simple reversible choice of y⊕f(x) will shown to be useful below.
• The circuit representation is
N N
|xi
Uf
|xi
|yi |y⊕f(x)i
• ForN = 1, the state
|Ψi= Ψ0,0|0,0i+ Ψ0,1|0,1i+ Ψ1,0|1,0i+ Ψ1,1|1,1i (1.25) then would be mapped to
Uf|Ψi= Ψ0,0|0,0⊕f(0)i+ Ψ0,1|0,1⊕f(0)i
+ Ψ1,0|1,0⊕f(1)i+ Ψ1,1|1,1⊕f(1)i. (1.26)
• Example: N = 1,f(x) = 1 We have
Uf|Ψi= Ψ0,0|0,1i+ Ψ0,1|0,0i+ Ψ1,0|1,1i+ Ψ1,1|1,0i. (1.27) or
Uf =
1.2. QUANTUM ALGORITHMS 13
• Example: N= 1, f(x) =x We have
Uf|Ψi= Ψ0,0|0,0i+ Ψ0,1|0,1i+ Ψ1,0|1,1i+ Ψ1,1|1,0i. (1.28) or
Uf =
1.2 Quantum algorithms
1.2.1 Deutsch–Jozsa algorithm
• A simple example for a problem that can be solved exponentially faster on a quantum computer than on a classical computer
• Problem: Given a function
f :{0,1}N → {0,1} (1.29) that is either constant (maps always to either 0 or 1) or balanced (returns 0 for exactly half of the input domain and 1 else), find out if it is constant or balanced.
• Classical solution: evaluate function for all possible inputs and stop as soon as answer is known
– Best case: first two evaluations differ⇒function is balanced – Worst case: first 2N−1 evaluations are identical ⇒ answer known
after 2N−1+ 1 evaluations
– For randomized selection of inputs: probability of misidentification afternevaluations is≤21n
• Quantum algorithm (guaranteed result after one evaluation):
N N
|0i H⊗N
Uf
H⊗N r
|1i H
The measuredr = 0 if and only iff is constant. If f is balanced r6= 0 will be measured.
• Explanation:
We start with the input state (Mark states in diagram above)
Ψ0=|0i⊗N|1i. (1.30) After the Hadamard operations, we have
Ψ1=
2XN−1 x=0
√ 1
2N+1|xi |0i − |1i
. (1.31)
To illustrate the mechanism, we remind ourself that forN = 2 (H⊗H)|00i= (H⊗1) 1
√2 |00i+|01i
, (1.32)
= 1
2 |00i+|10i+|01i+|11i
(1.33) and
H|1i= 1
√2 |0i − |1i
. (1.34)
ThenUf produces
Ψ2=
2XN−1 x=0
√ 1
2N+1|xi |0⊕f(x)i − |1⊕f(x)i
(1.35)
=
2XN−1 x=0
(−1)f(x)
√2N+1 |xi |0i − |1i
. (1.36)
Next we note
H|bi= 1
√2 X1 b0=0
(−1)bb0|b0i (1.37) withb∈ {0,1} or generally
H⊗N|xi= 1
√2N
2XN−1 z=0
(−1)x·z|zi, (1.38) where
x·z≡
N−1X
j=0
bitj(x)bitj(z)
mod 2 (1.39)
and bitj(x) is the value of thej-th bit of x.
1.2. QUANTUM ALGORITHMS 15 Therefore the final state is
Ψ3=
2XN−1 x,z=0
(−1)z·x+f(x) 2N |zi
|0i − |√ 1i 2
. (1.40)
Now iff(x) is constant, the amplitude of thez= 0 state is
2XN−1 x=0
(−1)f(x) 2N
2
= 1 (1.41)
and therefore with certaintyr= 0 will be measured. If f(x) is balanced thez= 0 amplitude is
2XN−1 x=0
(−1)f(x) 2N
2
= 0 (1.42)
and due to the normalization of the state a valuer6= 0 will be measured.
So with a single application of the quantum circuit, we know the answer.
• Run algorithm on sqc
1.2.2 Grover algorithm
• Problem:
Given a function
f :{0,1}N → {0,1} (1.43) that is 1 for one value ofx0 with 0≤x0<2N and 0 for all other values, findx0.
• Applications: Database search, cryptographic hash functions, factor n= p∗qwithpandqprime (classical test division up to√n)
• Classical solution requires O(2N) evaluations of the function
• Here, we illustrate a quantum algorithm which requires O(√
2N) function evaluations
• The quantum circuit is:
N N
|0i H⊗N
Gk
r
|1i H
with
N N
G
=
N N
Uf
Us
and
Us = H⊗N 2|0i h0| −1 H⊗N .
• Fork≈√
2N, we measurer=x0with high likelihood 1−O(1/2N)
1.2. QUANTUM ALGORITHMS 17
• Explanation:
We start with the input state (Mark states in diagram above)
Ψ0=|0i⊗N|1i. (1.44) After the Hadamard operations, we have
Ψ1=
2XN−1 x=0
√ 1
2N+1|xi |0i − |1i
. (1.45)
Neglecting the trivial last qubit, we can say that at this point the system is in state
|ψi ≡ |ψ1i= 1
√2N
2XN−1 x=0
|xi=
r2N−1
2N |αi+ 1
√2N |βi (1.46) with useful basis
|αi ≡ 1
√2N −1 X
x6=x0
|xi, (1.47)
|βi ≡ |x0i. (1.48)
We will find that the remaining operations live in the space spanned by
|αiand|βi.
It is easy to verify thatUf :|xi |yi 7→ |xi |y⊕f(x)iperforms a reflection about|αiin this space, i.e.,
Uf(a|αi+b|βi) =a|αi −b|βi. (1.49) Similarly
Us=H⊗N(2|0i h0| −1)H⊗N = 2|ψi hψ| −1 (1.50) i.e.,Usis a reflection about the vector|ψi. CombinedGtherefore performs a rotation in this space by
cos(θ/2) =
r2N −1
2N (1.51)
or
θ= 2
√2N
1 +O(1/2N)
. (1.52)
Illustrate:
Figure 6.3. The action of a single Grover iteration,G: the state vector is rotated byθtowards the superposition
|β⟩of all solutions to the search problem. Initially, it is inclined at angleθ/2 from|α⟩, a state orthogonal to|β⟩.
An oracle operationOreflects the state about the state|α⟩, then the operation 2|ψ⟩⟨ψ| −Ireflects it about|ψ⟩.
In the figure|α⟩and|β⟩are lengthened slightly to reduce clutter (all states should be unit vectors). After repeated Grover iterations, the state vector gets close to|β⟩, at which point an observation in the computational basis outputs a solution to the search problem with high probability. The remarkable efficiency of the algorithm occurs becauseθbehaves likeΩ(!
M/N), so onlyO(!
N/M) applications ofGare required to rotate the state vector close to|β⟩.
whereθis a real number in the range 0 toπ/2 (assuming for simplicity that M≤N/2; this limitation will be lifted shortly), chosen so that
sinθ=2√ M(N−M)
N . (6.14)
6.1.4 Performance
How many times must the Grover iteration be repeated in order to rotate|ψ⟩near|β⟩? The initial state of the system is|ψ⟩=!(N−M)/N|α⟩+!M/N|β⟩, so rotating through arccos!M/Nradians takes the system to|β⟩. Let CI(x) denote the integer closest to the real numberx, where by convention we round halves down, CI(3.5) = 3, for example. Then repeating the Grover iteration
R= CI
"
arccos!M/N θ
#
(6.15) times rotates|ψ⟩to within an angleθ/2≤π/4 of|β⟩. Observation of the state in the computational basis then yields a solution to the search problem with probability at least one-half. Indeed, for specific values ofMandNit is possible to achieve a much higher probability of success. For example, whenM≪Nwe haveθ≈sinθ≈2!M/N, and thus the angular error in the final state is at mostθ/2≈!M/N, giving a probability of error of at mostM/N. Note thatRdepends on the number of solutionsM, but not
Afterk applications
|ψ1+ki=Gk|ψ1i= cos(θk/2)|αi+ sin(θk/2)|βi. (1.53) We find
θk= (1 + 2k)θ . (1.54)
Forθk ≈π we have the optimal solution or k≈(π/4)√
2N. (1.55)
1.2.3 Parenthesis: Arithmetic gates, ancilla and garbage qubits, uncomputing
• We now address how to implement generic arithmetic functionsf(x) with x=
NX−1 j=0
bj2j, (1.56)
where bj∈ {0,1}.
• A circular left shiftCl with
Cl|bN−1, . . . , b0i=|bN−2, . . . , b0, bN−1i (1.57) can be implemented with SWAP gates. ExampleN = 4:
|b0i Cl
|b3i
|b1i |b0i
|b2i |b1i
|b3i |b2i
=
|b0i |b3i
|b1i |b0i
|b2i |b1i
|b3i |b2i
.
1.2. QUANTUM ALGORITHMS 19 IfbN−1= 0, this implements
f(x) = 2x . (1.58)
If bN−1 = 1, the circular left shift results in an odd number, however, which we may not wish for an implementation off(x) = 2x.
• A left shift
Sl|bN−1, . . . , b0i=|bN−2, . . . , b0,0i (1.59) can be implemented if we add a so-calledancilla qubit with fixed value
|0ito the circuit, resulting in an additional variablegarbage qubit. We again illustrate forN= 4:
|b0i
Cl
|0i
|b1i |b0i
|b2i |b1i
|b3i |b2i
Ancilla qubit|0i |b3iGarbage qubit .
This operation again coincides withf(x) = 2x, however, has a more gra- cious overflow behavior (known from, e.g., C code) forbN−1= 1.
• A circular right shiftCr with
Cr|bN−1, . . . , b0i=|b0, bN−1, . . . , b1i (1.60) can again be implemented with SWAP gates. ExampleN = 4:
|b0i Cr
|b1i
|b1i |b2i
|b2i |b3i
|b3i |b0i
=
|b0i |b1i
|b1i |b2i
|b2i |b3i
|b3i |b0i
.
Ifb0= 0, this implements
f(x) =x/2. (1.61)
However forb0= 1 (for odd numbers), we do not obtain a sensible result for division by two.
• A right shift
Sr|bN−1, . . . , b0i=|0, bN−1, . . . , b1i (1.62) can again be implemented with ancilla and garbage qubits. We again illustrate forN = 4:
|b0i
Cr
|b1i
|b1i |b2i
|b2i |b3i
|b3i |0i
Ancilla qubit|0i |b0iGarbage qubit .
This operation coincides with f(x) =x/2 for allx.
• The need for ancilla and garbage qubits originates from the restriction to use reversible (unitary) gates on a quantum computer.
• Since the value of a garbage qubit is variable, we cannot reuse it as an an- cilla bit for another gate. We can, however, use intermediate information and thenuncompute it to restore the ancilla bit.
Example: ImplementUf for
f(x) =
(1 for 2x= 10,
0 else . (1.63)
ForN = 4, this can be implemented as
|b0i
Uf
|b0i
|b1i |b1i
|b2i |b2i
|b3i |b3i
|0i |0i
|yi |y⊕f(x)i
=
1.2. QUANTUM ALGORITHMS 21
|b0i
Cl Cr
|b0i
|b1i |b1i
|b2i |b2i
|b3i |b3i
|0i |0i
|yi |y⊕f(x)i
,
where the C4NOT operation only acts forx= 10 (binary 1010).
This “uncomputation” now allows for multiple applications of thisUf with only a single overall ancilla qubit.
• Next, we consider the function
f(x) =x+ 1. (1.64)
This can be implemented using elementary “half-adder” gates
|ai
O+,1/2
|ai
|bi |a⊕bi= Sum Ancilla qubit|0i |abi= Carry
=
|ai |ai
|bi |a⊕bi
|0i |abi
.
We combine half-adders to implement the function. For N=3, e.g.,
|1i
O+,1/2
|1i
|b0i |b00i
|0i
O+,1/2
|b0i
|b1i |b01i
|0i
O+,1/2
|b0b1i
|b2i |b02i
|0i |b0b1b2i
with
x+ 1 =
N−1X
j=0
b0j2j. (1.65)
• We can also add more generally
f(x) =x+z (1.66)
with
z=
NX−1 j=0
cj2j. (1.67)
For this we need to define a full-adder gate
|ai
O+
|ai
|bi |bi
|ci |a⊕b⊕ci= Sum Ancilla qubit|0i |ab+c(a⊕b)i= Carry
=
|ai |ai
|bi |bi
|ci |a⊕b⊕ci
|0i |ab+c(a⊕b)i
.
1.2. QUANTUM ALGORITHMS 23 We combine full-adders to implement the function. For N=3, e.g.,
|0i
O+
|b0i
|c0i |b00i
|0i
O+
|b1i
|c1i |b01i
|0i
O+
|b2i
|c2i |b02i
|0i with
x+z=
NX−1 j=0
b0j2j, (1.68)
where we do not write the values of the garbage qubits.
• Similarly, we can implement subtraction.
• Finally, we consider multiplication ofxandz, i.e., f(x) =xz=
NX−1 j,j0=0
bjcj02j+j0 =
NX−1 j=0
bjSlj(z), (1.69)
where Sjl(z) implements j left-shifts of the number z as defined above.
We note that we can implement binary multiplication as a combination of such shifts and addition.
1.2.4 Example: Solving an equation using Grover’s algo-
rithm
5/9/19, 1'23 PMgrover Page 1 of 20http://localhost:8888/nbconvert/html/grover.ipynb?download=false
In [1]:importsqc importnumpyasnp importmatplotlib.pyplotasplt
Contr ol-U gates (see also Pr oblem Set 2, Pr oblem 1)
In [2]:defA(i,o): returno.Rz(i,np.pi/4.0).H(i).Rz(i,np.pi/2.0) defAdg(i,o): returno.Rz(i,-np.pi/2.0).H(i).Rz(i,-np.pi/4.0) defCH(i,t,o):# i=control, t=target returnA(t,Adg(t,o).CNOT(i,t)) defCRz(i,t,phi,o): returno.Rz(t,phi/2.).CNOT(i,t).Rz(t,-phi/2.).Rz(i,phi/2.).CNOT(i, t) op=sqc.operator(2) foriinrange(4): st=sqc.state(2,v=[1ifi==jelse0forjinrange(4)]) print("Applying CH(0,1) to %s gives:\n%s\n"%(str(st),str(CH(0,1, op)*st))) print("Applying CRz(0,1,Pi/2) to %s gives:\n%s\n"%(str(st),str(C Rz(0,1,np.pi/2.,op)*st)))5/9/19, grover Pagehttp://localhost:8888/nbconvert/html/grover.ipynb?download=false
gate (see also Lectur e Section 1.1.7) 𝐶
2𝑋
1/𝑛 =𝐻𝐻𝑋1/𝑛𝑅𝜋/𝑛 Applying CH(0,1) to 1 * |00> gives: 0.9999999999999998 * |00> Applying CRz(0,1,Pi/2) to 1 * |00> gives: (1+0j) * |00> Applying CH(0,1) to 1 * |01> gives: 0.7071067811865475 * |01> + 0.7071067811865474 * |11> Applying CRz(0,1,Pi/2) to 1 * |01> gives: (1+0j) * |01> Applying CH(0,1) to 1 * |10> gives: 0.9999999999999998 * |10> Applying CRz(0,1,Pi/2) to 1 * |10> gives: (1+0j) * |10> Applying CH(0,1) to 1 * |11> gives: 0.7071067811865474 * |01> + -0.7071067811865475 * |11> Applying CRz(0,1,Pi/2) to 1 * |11> gives: (2.220446049250313e-16+1j) * |11>5/9/19, 1'23 PMgrover Page 3 of 20http://localhost:8888/nbconvert/html/grover.ipynb?download=false
In [3]:defCrootX(i,t,n,o): returnCH(i,t,CRz(i,t,np.pi/n,CH(i,t,o))) defCNOT(i,j,o): returno.CNOT(i,j) defC2rootX(i,j,t,n,o):#i,j=control; t=target returnCrootX(i,t,2.*n,CNOT(i,j,CrootX(j,t,-2.*n,CNOT(i,j,CrootX(j ,t,2.*n,o))))) op=sqc.operator(3) foriinrange(8): st=sqc.state(3,v=[1ifi==jelse0forjinrange(8)]) print("Applying C2NOT(0,1,2) to %s gives:\n%s\n"%(str(st),str(C2 rootX(0,1,2,1,op)*st)))
(see also Lectur e Section 1.1.7)
In Problem Set 02, we will learn a much faster implementation, that requires additional worker qubits.𝐶
𝑛𝑋
1/𝑚Applying C2NOT(0,1,2) to 1 * |000> gives: 0.999999999999999 * |000> Applying C2NOT(0,1,2) to 1 * |001> gives: 0.9999999999999989 * |001> Applying C2NOT(0,1,2) to 1 * |010> gives: 0.9999999999999989 * |010> Applying C2NOT(0,1,2) to 1 * |011> gives: 0.9999999999999988 * |111> Applying C2NOT(0,1,2) to 1 * |100> gives: 0.9999999999999989 * |100> Applying C2NOT(0,1,2) to 1 * |101> gives: 0.9999999999999989 * |101> Applying C2NOT(0,1,2) to 1 * |110> gives: 0.9999999999999989 * |110> Applying C2NOT(0,1,2) to 1 * |111> gives: 0.9999999999999991 * |011>5/9/19, 1'23 PMgrover Page 4 of 20http://localhost:8888/nbconvert/html/grover.ipynb?download=false
In [4]:defCnrootX(c,t,m,o):#c=array of n control qubits; t=target qubit assert(len(c)>0) iflen(c)==1: returnCrootX(c[0],t,m,o) i=[c[0]] j=[c[1]] r=c[2:] returnCnrootX(r+i,t,2.*m,CnrootX(r+i,j[0],1.,CnrootX(r+j,t,-2.* m,CnrootX(r+i,j[0],1.,CnrootX(r+j,t,2.*m,o))))) op=sqc.operator(4) foriinrange(16): st=sqc.state(4,v=[1ifi==jelse0forjinrange(16)]) print("Applying CnNOT([0,1,2],3) to %s gives:\n%s\n"%(str(st),st r(CnrootX([0,1,2],3,1,op)*st)))
5/9/19, 1'23 PMgrover Page 5 of 20http://localhost:8888/nbconvert/html/grover.ipynb?download=false
Applying CnNOT([0,1,2],3) to 1 * |0000> gives: 0.9999999999999921 * |0000> Applying CnNOT([0,1,2],3) to 1 * |0001> gives: 0.9999999999999909 * |0001> Applying CnNOT([0,1,2],3) to 1 * |0010> gives: 0.9999999999999921 * |0010> Applying CnNOT([0,1,2],3) to 1 * |0011> gives: 0.9999999999999909 * |0011> Applying CnNOT([0,1,2],3) to 1 * |0100> gives: 0.9999999999999907 * |0100> Applying CnNOT([0,1,2],3) to 1 * |0101> gives: 0.9999999999999912 * |0101> Applying CnNOT([0,1,2],3) to 1 * |0110> gives: 0.9999999999999913 * |0110> Applying CnNOT([0,1,2],3) to 1 * |0111> gives: 0.9999999999999909 * |1111> Applying CnNOT([0,1,2],3) to 1 * |1000> gives: 0.999999999999991 * |1000> Applying CnNOT([0,1,2],3) to 1 * |1001> gives: 0.9999999999999912 * |1001> Applying CnNOT([0,1,2],3) to 1 * |1010> gives: 0.9999999999999908 * |1010> Applying CnNOT([0,1,2],3) to 1 * |1011> gives: 0.9999999999999908 * |1011> Applying CnNOT([0,1,2],3) to 1 * |1100> gives: 0.9999999999999906 * |1100> Applying CnNOT([0,1,2],3) to 1 * |1101> gives: 0.9999999999999907 * |1101> Applying CnNOT([0,1,2],3) to 1 * |1110> gives: 0.999999999999991 * |1110> Applying CnNOT([0,1,2],3) to 1 * |1111> gives: 0.999999999999991 * |0111>
5/9/19, grover Pagehttp://localhost:8888/nbconvert/html/grover.ipynb?download=false
Cir cular shift
In [5]:defSWAP(i,j,o): returno.CNOT(i,j).CNOT(j,i).CNOT(i,j) defCl(mask,o): foriinmask[1:]: o=SWAP(mask[0],i,o) returno defCr(mask,o): foriinreversed(mask[:-1]): o=SWAP(mask[-1],i,o) returno op=sqc.operator(4) st=sqc.state(4,v=[0,1]+[0]*14) foriinrange(4): print("Cl^%d |0001> = %s"%(i,str(st))) st=Cl([0,1,2],op)*st st=sqc.state(4,v=[0,1]+[0]*14) foriinrange(4): print("Cr^%d |0001> = %s"%(i,str(st))) st=Cr([0,1,2],op)*stGr over sear ch for 2x=10 (see Lectur e Section 1.2.2)
Cl^0 |0001> = 1 * |0001> Cl^1 |0001> = 1.0 * |0010> Cl^2 |0001> = 1.0 * |0100> Cl^3 |0001> = 1.0 * |0001> Cr^0 |0001> = 1 * |0001> Cr^1 |0001> = 1.0 * |0100> Cr^2 |0001> = 1.0 * |0010> Cr^3 |0001> = 1.0 * |0001>
5/9/19, 1'23 PMgrover Page 7 of 20http://localhost:8888/nbconvert/html/grover.ipynb?download=false
In [6]:nqubits=4 expected_theta=2.*np.arccos(np.sqrt((2**nqubits-1.)/(2**nqubits))) optimal_k=int(np.round(np.pi/4.*np.sqrt(2**nqubits))) print("Optimal_k = %d"%optimal_k) plt.figure(figsize=(6,6)) plt.xlim(-1,1) plt.ylim(-1,1) plt.quiver([0],[0],[0,1],[1,0], color=['gray'],scale=3) plt.text(0.75,0,"|alpha>") plt.text(0,0.75,"|beta>") # TODO: theta_k plt.quiver([0],[0],[np.cos(expected_theta*(i+0.5))foriinrange(opti mal_k+1)], [np.sin(expected_theta*(i+0.5))foriinrange(optimal_k+1)], color=['r','b','g','black'],scale=4) plt.show() expected_theta_deg=expected_theta/np.pi*180. print("Optimal_angle = %g"%((optimal_k+0.5)*expected_theta_deg))
5/9/19, 1'23 PMgrover Page 8 of 20http://localhost:8888/nbconvert/html/grover.ipynb?download=false
In [7]:print("Startup Grover Search") print("---") Nbits=nqubits+2# bits for x, 1 ancilla bit, 1 for y defpr(i,start,width): return(i//2**start)%(2**width) # Psi0 psi0=sqc.operator(Nbits).X(nqubits+1)*sqc.state(Nbits, basis=["|%d>|%d>|%d>"%(pr(i,0,nqubits),pr(i,nqubits,1), pr(i,nqubits+1,i))foriinrange(2**Nbits)]) print("|Psi0> = ") print(psi0) print("")# TODO: continue here # Psi1 psi1=sqc.operator(Nbits).H(0).H(1).H(2).H(3).H(5)*psi0 print("|Psi1> = ") print(psi1) print("")
Optimal_k = 3 Optimal_angle = 101.343