·
Einf¨ uhrung in die Theorie dynamischer, insbesondere linearer Systeme
U. Mortensen
Fachbereich Psychologie und Sportwissenschaften, Institut III Westf¨alische Wilhelms-Universit¨at
M¨unster, 2000
Revidierte Version 30. 08. 2007 letzte ¨Anderung: 23. 05. 2008
Inhaltsverzeichnis
1 Dynamische Systeme 5
1.1 Dynamische Systeme: allgemeine Begriffe . . . 5
1.2 Lineare Systeme . . . 10
1.2.1 Allgemeine Charakterisierung . . . 10
1.2.2 Die L¨osungen eines linearen Systems . . . 12
1.2.3 Die Exponentialmatrix . . . 12
1.2.4 Die Dirac-Impuls-Funktion und die Impulsantwort-Matrix . . . 18
1.2.5 Die Operator-Schreibweise . . . 20
1.2.6 Zur Berechnung der Impulsmatrix . . . 22
1.2.7 Stabilit¨at linearer Systeme; Eigenfrequenzen . . . 23
1.2.8 Anmerkungen zum Zustandsbegriff . . . 24
1.2.9 Lineare Systemen-ter Ordnung . . . 25
1.2.10 System- und Transferfunktionen . . . 34
1.2.11 Minimum-Phasen-Systeme . . . 42
1.2.12 Transferfunktionen und Partialbruchzerlegung . . . 45
1.2.13 Der Fall einfacher Pole . . . 47
1.2.14 Der Fall mehrfacher Pole . . . 49
1.2.15 Elementare Systemelemente . . . 50
1.2.16 Elementare ¨Ubertragungsglieder . . . 50
1.2.17 Teilsysteme zweiter Ordnung . . . 53
1.2.18 Graphische Repr¨asentationen und Maßeinheiten . . . 55
1.2.19 Filter und ihre Charakterisierung . . . 57
1.2.20 Maximale Antwort linearer Filter; Matched Filter . . . 63
1.2.21 Energie und Leistung . . . 65
1.2.22 Linearisierung nichtlinearer Systeme . . . 72
2 Die allgemeine Theorie der Signalentdeckung 81
2.1 Entdeckenswahrscheinlichkeiten als bedingte Wahrscheinlichkeiten . . . . 83
2.2 Der Likelihood-Quotient f¨ur Weißes Rauschen . . . 84
2.3 Spezielle Modelle des Entdeckens . . . 89
2.3.1 Peak-Detection . . . 90
2.3.2 Wahrscheinlichkeitssummation . . . 90
2.4 Psychometrische Funktionen . . . 92
2.4.1 Allgemeine Modelle . . . 92
2.4.2 Das Quick-Modell: W-Summation zwischen Kan¨alen . . . 95
2.4.3 Zeitliche Wahrscheinlichkeitssummation . . . 100
3 Visuelle Psychophysik 107 3.1 Psychophysik im Zeit- und Ortsbereich . . . 107
3.2 Erste empirische Befunde . . . 108
3.3 Systemidentifikation im Zeitbereich . . . 109
3.3.1 Sch¨atzung der Amplitudencharakteristik . . . 113
3.3.2 Die Perturbationsmethode . . . 120
3.3.3 Peak-Detection versus Wahrscheinlichkeitssummation . . . 123
3.4 Systemidentifikation im Ortsbereich . . . 127
3.4.1 Das visuelle System als einzelner Kanal . . . 127
3.4.2 Die direkte Sch¨atzung der Impulsantwort im Ortsbereich . . . 130
3.4.3 Neuronale Kan¨ale: Orientierungen . . . 134
3.4.4 Neuronale Kan¨ale: Ortsfrequenzen . . . 136
3.4.5 Neuronale Kan¨ale: Kanten-, Linien- und Gitterdetektoren . . . 139
3.4.6 Neuronale Kan¨ale als Matched Filter . . . 143
A Fourier- und Laplace-Transformationen 151 A.1 Komplexe Zahlen . . . 151
A.2 Fourier-Reihen . . . 155
A.2.1 Periodische Funktionen . . . 155
A.2.2 Superpositionen . . . 156
A.2.3 Die Orthogonalit¨atsrelationen der Sinus- und Kosinusfunktionen . 158 A.3 Fouriertransformierte . . . 161
A.3.1 Definition der Fouriertransformierten . . . 161
A.3.2 Einige allgemeine S¨atze . . . 163
A.3.3 Die Dirac-Delta Funktion . . . 167
A.4 Fourier-Transformationen spezieller Funktionen . . . 169
A.4.1 Die Sinus- bzw. Kosinusfunktion . . . 169
A.4.2 Die Exponentialfunktion . . . 169
A.4.3 Eine Konstante . . . 172
A.4.4 Die Funktion 1/x . . . 172
A.4.5 Die Schrittfunktion . . . 173
A.4.6 Der Balken . . . 173
A.4.7 Die Gabor-Funktion . . . 174
A.4.8 Hermite-Funktionen . . . 175
A.5 Hilbertransformierte . . . 176
A.6 Laplace-Transformierte . . . 178
A.7 Die Schwartzsche Ungleichung . . . 179
A.8 2-dimensionale Signale . . . 180
A.8.1 Allgemeine Definition . . . 180
A.8.2 Gabor-Muster . . . 182
B Stochastische Prozesse und Verteilungen 183 B.1 Stochastische Prozesse . . . 183
B.2 Die Weibull-Verteilung . . . 192
C Literatur 195
Symbole und Bezeichnungen
Es wird von den folgenden Symbolen bzw. Bezeichnungen Gebrauch gemacht:
R Menge der reellen Zahlen
N Menge der nat¨urlichen Zahlen 0, 1, 2,· · ·
C Menge der komplexen Zahlenz=a+jb,a, b∈R, j=√
−1 exp(x) ex
log nat¨urlicher Logarithmus (zur Basise) log10 Logarithmus zur Basis 10
Kapitel 1
Dynamische Systeme
1.1 Dynamische Systeme: allgemeine Begriffe
Sprungfedern, Planetensysteme, Pendel, interagierende Populationen wie die der F¨uchse und Hasen, Neurone und Netze von Neuronen sind Beipiele f¨ur dynamische Systeme; diese Systeme m¨ussen also trotz ihrer Verschiedenheit wesentliche Aspekte gemein haben. Die Definition des Begriffs des dynamischen Systems wird dementsprechend einigermaß en abstrakt sein. Es soll gleichwohl auf allzu große mathematische Strenge verzichtet werden, da sie den Rahmen des Textes sprengen w¨urde; der interessierte Leser sei auf die Literatur, etwa Arnol’d (1980), J¨anich (1983) oder Arrowsmith und Place (1990) verwiesen. Es gen¨ugt f¨ur unsere Zwecke, ein gewisses intuitives Verst¨andnis der Begriffsbildungen zu erhalten, das die qualitative Betrachtung dynamischer Systeme erleichtern soll.
Ohne Beschr¨ankung der Allgemeinheit l¨aßt sich sagen, dass ein System zu einem be- stimmten Zeitpunkt in einem bestimmten Zustand ist; so hat ein schwingendes Pendel zu einem Zeitpunktteine bestimmte Auslenkungφ(t) (Abweichung von der Vertikalen) sowie eine bestimmte Geschwindigkeitv(t), und φ(t) undv(t) zusammen definieren den Zustand des Pendels. Man sieht hier bereits, dass bei der Charakterisierung der Zust¨an- de eine gewisse Willk¨urlichkeit herrscht, denn von der Beschaffenheit des Materials, von seinem Alter und einer Reihe anderer Eigenschaften sehen wir bei unserer Zustandsbe- schreibung ab. Betrachten man ein Neuron, so kann sein Membranpotential zur Zeittals sein Zustand zur Zeitterkl¨art werden, und wieder hat man dabei von vielen Eigenschaf- ten des Neurons, die man ebenso als zustandsdefinierend betrachten k¨onnte, abstrahiert.
Die Wahl der betrachteten Zust¨ande ist somit ein Teil der Theorie, die ¨uber das Sy- stem entwickelt wird. F¨ur die Definition des Begriffs des dynamischen Systems ist dieser Aspekt der Willk¨urlichkeit belanglos.
Der Zustand des betrachteten Systems im Zeitpunkt t soll durch x(t) repr¨asentiert werden, wobeix(t) als Vektor
x(t) = (x1(t),· · ·, xn(t))′
aufgefaßt wird. Die n Komponentenxi(t), 1≤i≤n, von x(t) repr¨asentieren dann be- stimmte Zustandsaspekte und k¨onnen als Koordinaten eines Punktesxbzw.x(t) imRn
aufgefaßt werden. Dementsprechend werden wir die Ausdr¨ucke ”Punkt” und ”Zustand”
synoym verwenden. Diexi(t) sind Funktionen der Zeit. Der Verlauf dieser Zustands¨ande- rungen definiert die Dynamik des Systems. Die Definition des Begriffs des dynamischen Systems wird dementsprechend auf einen ”Zustandsraum” als Teilraum des Rn bezug nehmen und eine allgemeine Charakterisierung der Dynamik enthalten.
Ist nun ein Zustand durch einen Punktx(t) gegeben, so bedeutet die Ver¨anderung des Zustands nach s Zeiteinheiten den ¨Ubergang zu einem anderen Punkt x(t+s) = (x1(t+s),· · ·, xn(t +s))′. Formal wird also die Dynamik durch eine Abbildung von Punkten imRn auf Punkte imRn erkl¨art. Dementsprechend hat man dann die
Definition 1.1.1 Es sei M ⊂Rn ein offenes Gebiet1 desRn und φ:R×M →M sei eine stetige Abbildung, die f¨ur allex∈M den Bedingungen
(i) φ(0, x) =x
(ii) φ(s, φ(t, x)) =φ(t+s, x) f¨ur alles,t∈R
gen¨ugt. Dann heißtφdynamisches System, undcheißtPhasen-oderZustandsraum.x∈ M heißt ZustandoderPhasenpunkt.Das Paar(M, φ)heißtZustands- oderPhasenfluß.
Gem¨aß Definition 1.1.1 ist ein dynamisches System abstrakt als eine Abbildung φdefi- niert, und zwar werden Elemente von R×M auf Punkte inc abgebildet. Sindc undφ gegeben, so hat man das System spezifiziert. Ein Element ausR×M ist ein Paar (t, x), durch das ein Zeitpunkt und ein Zustand festgelegt werden. Die Abbildung φ ordnet diesem Paar, d.h. dem Zustand xzum Zeitpunktt, einen bestimmten anderen Zustand y ∈M zu, n¨amlichy =φ(t, x). Durchφwerden die Zustandstransformationen oder der Fluß der Zust¨ande festgelegt; daher der Ausdruck Zustandsfluß f¨ur das Paar (M, φ). (Der synonym gebrauchte AusdruckPhasef¨ur Zustand geht auf Betrachtungen in der Physik zur¨uck.) Die Bedingungen (i) und (ii) in Definition 1.1.1 heißen dementsprechend auch Flußaxiome.
F¨ur die in Definition 1.1.1 eingef¨uhrte Abbildung φist Stetigkeit gefordert worden;
dies bedeutet, dass kein sprunghafter ¨Ubergang von einem Zustand zu einem anderen erfolgen soll; jeder ¨Ubergang ben¨otigt Zeit. Die Implikationen dieser Forderung werden anhand des in der folgenden Definition eingef¨uhrten Begriffs, der es erlaubt, weitere Eigenschaften eines dynamischen Systems herzuleiten, deutlich werden.
Definition 1.1.2 Es sei M ⊂ Rn der Zustandsraum eines dynamischen Systems und es sei ϕx : R → M, ϕx(t) 7→ y ∈ M, eine Abbildung, die f¨ur spezielles x ∈ M und t∈Rden Zustandy∈M festlegt, den das System vonxausgehend nacht Zeiteinheiten annimmt. Dann heißt ϕx Flußlinie oder Bewegung des Punktes x unter Wirkung des Flusses (M, φ).Die Menge ϕx(R) der Punkte, die man vonx ausgehend erreicht, heißt die durch xgehende Trajektorie(Bahn, Orbit, Phasenkurve) des dynamischen Systems φ.
Eine Trajektorie des dynamischen Systemsφist dementsprechend dasBildder Abbildung ϕx. Nat¨urlich istϕx(t) =φ(t, x). W¨ahrend aberφf¨urbeliebiges xundt den Zustandy
1Die Randpunkte des Gebietes geh¨oren nicht zuM.
definiert, in denxnachtZeiteinheiten ¨ubergeht, betrachtetϕxdiesen ¨Ubergang nur f¨ur ein speziellesx∈M, d.h. betrachtet manϕx, so betrachtet man einen speziellen, durch den Punktxverlaufenden Prozeß. Dementsprechend ist die KenntnisallerAbbildungen, d.h. aller Flußlinienϕx gleichbedeutend mit der Kenntnis vonφ. Man erh¨alt nun sofort die im folgenden Satz enthaltenen Folgerungen:
Satz 1.1.1 Es gelten die folgenden Aussagen:
1. ϕx(0) = xf¨ur alle x∈M, d.h. der Zustand ver¨andert sich nicht, ohne dass Zeit vergeht.
2. Es seiy=ϕx(t0)∈M; dann l¨aßt sich auch eine Flußlinie f¨ury erkl¨aren. Offenbar istϕy(t) =ϕx(t0+t) f¨ur allet∈R.
3. Haben zwei Flußlinienϕxundϕy einen gemeinsamen Punkt, so sind sie ¨uberhaupt identisch; zweinicht identische Flußlinien k¨onnen sich nicht kreuzen.
Die Folgerungen 1. und 2. sind unmittelbar klar. Die Folgerung 3. sieht man wie folgt ein:
es gelte etwaϕy(t) =ϕx(t0+t). Dies heißt abery=ϕx(t0), und nach Satz 1.1.1 erreicht man alle Zust¨andez=ϕy(t) ebenfalls, wenn man vonxausgehend die Zust¨andeϕx(t0+ t) bestimmt. Dies heißt, dass die Menge ϕy(R) der Punkte, die man von y ausgehend erreicht, gleich der Mengeϕx(R) der Punkte ist, die man vonxausgehend erreicht; die durch x und y gehenden Trajektorien sind also gleich. Da sich aus ϕy(t) =ϕx(t0+t) die Gleichheit der Trajektorien ergibt, folgt aus derUngleichheitder Trajektorienϕx(R) und ϕy(R) auch, dass es keine Punkte xund y geben kann, f¨ur die ϕy(t) = ϕx(t0+t) gilt. Durch jeden Punktx∈M kann alsonur eineTrajektorie gehen.
Es sollen nun einige Typen von Trajektorien charakterisiert werden; anschließend wird gezeigt, dass es nur diese Typen gibt:
Definition 1.1.3 Gilt ϕx(t) =x f¨ur alle t ∈ R, so heißt x ein Fixpunkt des durchφ definierten dynamischen Systems. Existiert einτ0= inf{t0|ϕx(t+t0) =ϕx(t0)}2,τ0>0, derart, dass ϕx(t+τ0) = ϕx(t), so heißt ϕx periodisch und τ0 dementsprechend die Periode.Giltϕx(t0)6=ϕx(t1)f¨ur t06=t1, so heißtϕx injektiv.3
Die Bedeutung dieser Begriffe wird in der Aussage des folgenden Satzes verdeutlicht, die auch f¨ur qualitative Betrachtungen dynamischer Systeme von Bedeutung ist:
Satz 1.1.2 Die Flußlinien des Systems sind entweder Fixpunkte, oder sie sind periodisch, oder sie sind injektiv.
Beweis: Den Beweis des Satzes findet man etwa in Arnol’d (1980), J¨anich (1983), Ar- rowsmith und Place (1989).
2inf steht f¨urinfimum; dies ist in diesem Fall die kleinste Zahl der in {· · ·} angegebenen Menge.
Dementsprechend soll alsoτ0≤t0f¨ur allet0 gelten.
3Allgemein heißt eine Abbildung f : A→ B injektiv, wenn f¨ur allex1 und x2 aus A folgt, dass x1=x2fallsf(x1) =f(x2) ist. In Definition 1.1.2 ist aberϕxals Abbildung definiert worden.
In der Abb. 1 sind die drei Typen von Flußlinien dargestellt; Abb. 2 enth¨alt die Flußlinien, die sich bei einem ebenen Pendel ergeben. Die wie eine Acht aussehende Trajektorie darf nicht als sich kreuzende Flußlinie aufgefaßt werden, denn nach Satz 1.1.2 gibt es keine Flußlinien, die sich kreuzen; der ”Kreuzungspunkt” ist in der Tat eine Flußlinie f¨ur sich, n¨amlich einFixpunkt; ger¨at das System in diesen Zustand, so verharrt es dort, d.h. es finden keine Ver¨anderungen der xi statt. Beim Pendel ist dieser Zustand z.B. dann erreicht, wenn es zur Ruhe gekommen ist und senkrecht herunterh¨angt. Der Fixpunkt definiert einen Gleichgewichtszustand.
Die Definition des dynamischen Systems durch die Abbildungφund die der Flußlinien ϕx implizieren also, dass die Bewegungen im Zustands- oder Phasenraum in nur drei Klassen zerlegt werden k¨onnen. Die Tatsache, dass es f¨ur einen Punkt (Zustand) x ∈ M nur eine Trajektorie geben kann, die durch ihn hindurchf¨uhrt, bedeutet, dass die Kenntnis vonxsofort auch die Kenntnis des Prozesses, d.h. des Verlaufs der ¨Uberg¨ange der Zust¨ande ineinander, bedeutet. Der Prozeß ist insgesamt eindeutig bestimmt oder determiniert.
Bis jetzt ist zwar ein dynamisches System als eine Abbildungφdefiniert worden, aber es ist noch unklar, wie man zu einer konkreten Charakterisierung des Verhaltens eines solchen Systems gelangen kann. MitVerhaltensind dabei die Bewegungen im Zustands- raum gemeint. Nun bedeutet die Kenntnis von φ nach dem bisher Gesagten auch eine Kenntnis des Verhaltens, und so kann man sagen, dass φeine funktionale Beschreibung des Systems ist. Umgekehrt ist man h¨aufig daran interessiert, aus Beobachtungen des Verhaltens auf eine funktionale, durch Definition einer Abbildung φgegebene Beschrei- bung des Systems zu kommen. M¨oglichkeiten, φ n¨aher zu charakterisieren, sollen jetzt angegeben werden.
Die Dynamik eines Systems ¨außert sich in den Bewegungen der Zustandspunkte im Phasenraum M. Die Bewegungen, d.h. die Zustandsver¨anderungen, k¨onnen, abh¨angig vom Ort in c schnell oder langsam sein. Wir k¨onnen also jedem Punkt x ∈ M eine Geschwindigkeitv(x) zuordnen. Denn durchxgeht nur eine Flußlinie, und deshalb kann es inxauch nur eine Geschwindigkeitv(x) geben.v(x) ist ein Maß f¨ur die Ver¨anderung der Flußlinie in x und es liegt deshalb nahe, sie ¨uber einen Differentialquotienten zu definieren:
Definition 1.1.4 Die Ableitung
v(x) =dϕx(t)/dt|t=0
heißtPhasengeschwindigkeitdes Flusses(M, φ)im Punktx. Die Abbildung v:M →Rn heißt Vektorfeldauf M.
Der Punktxist durch einen Vektor definiert, und deshalb ist v(x) ebenfalls ein Vektor.
Dies kommt noch einmal in der Definition des Vektorfeldes v zum Ausdruck. Jedem Punkt incwird ein Punkt inRn zugeordnet, dessen Koordinaten eben die Komponenten des Vektors vsind.
x∈M ist ein Zustand des Systems, undϕx beschreibt die Transformation vonxals Funktion vont. v(x) gibt dann die Ver¨anderung der Flußlinie oder Trajektorie inxan.
Dementsprechend kann man auch ˙xf¨urv(x) schreiben. Man hat dann die
Definition 1.1.5 Es sei M ⊂Rn ein Zustandsraum eines dynamischen Systemsφund v das φentsprechende Vektorfeld. Dann heißt
˙
x=v(x) (1.1)
die durch das Vektorfeld v definierte Differentialgleichung (abgek¨urzt: Dgl). c heißt der Phasen- oder Zustandsraumder Dgl (1.1). Die Flußlinieϕx heißtL¨osungder Dgl (1.1), wenn dϕx(t)/dt|t=o = v(ϕx(τ)) f¨ur τ = t, a < t < b, wobei a = −∞ und b = +∞ zugelassen sind. Giltϕx(t0) =x0∈M f¨ur a < t0< b, so sagt man, dass die L¨osung der Anfangsbedingungϕx(t0) =x0 gen¨ugt.
Die Dgl (1.1) ist ein System von Differentialgleichungen; ausgeschrieben erh¨alt man
˙
x1 = v1(x1,· · ·, xn)
˙
x2 = v2(x1,· · ·, xn) ...
˙
xn = vn(x1,· · ·, xn) (1.2) Dievi sind dabei Funktionen derxj=xj(t). Ist das Systemφbekannt, so kann es duch das zugeh¨orige System von Dgln (1.2) beschrieben werden. Auf der linken Seite treten nur Ableitungen erster Ordnung auf, und auf der rechten Seite findet man nur Funktionen derxi, nicht aber ihre Ableitungen:
Ein dynamisches System ist also stets durch ein System von Differentialgleichungen erster Ordnung repr¨asentierbar.
Es sollte an hier Stelle angemerkt werden, dass durch (1.1) deterministische dyna- mische Systeme beschrieben werden. Stochastische Irregularit¨aten des Systemverhaltens gehen bei der Beschreibung durch (1.1) nicht mit ein. Das Verhalten neuronaler Systeme enth¨alt aber stochastische Komponenten, so dass eigentlich stochastische dynamische Sy- steme betrachtet werden m¨ussen. Die Diskussion solcher Systeme setzt aber die Kenntnis des Begriffs des deterministischen Systems voraus. Auf die stochastischen Aspekte wird sp¨ater eingegangen, es gen¨ugt an dieser Stelle, sich auf die Klasse der deterministischen Systeme zu beschr¨anken.
Ist ein dynamisches System durch ein System von Dgln charakterisierbar, so kann man umgekehrtAnnahmen¨uber ein System durch die Formulierung entsprechender Dgln artikulieren. Bestimmte — nicht alle — Systeme lassen sich auch durch bestimmte Funk- tionen, die Impuls- und die Transferfunktion, charakterisieren; darauf wird sp¨ater aus- f¨uhrlich eingegangen, denn von dieser M¨oglichkeit wird bei Anwendungen der Theorie der Systeme auf die Psychophysik ausgiebig Gebrauch gemacht. Impuls- und Transferfunkti- on stehen allerdings in einer bestimmten Beziehung zu dem System von Dgln, durch die das System beschrieben werden soll. Damit erl¨autert werden kann, wie die empirisch be- stimmten Impuls- und Transferfunktionen interpretiert werden k¨onnen, sollen zun¨achst die Systeme von Dgln weiter betrachtet werden.
EineL¨osungf¨ur das System von Dgln besteht in einem Vektor x(t) = (x1(t),· · ·, xn(t))′,
dessen Komponentenxj(t) Funktionen sind, die den in Bedingung (1.2) genannten For- derungen gen¨ugen. Die x1(t),· · ·, xn(t) k¨onnen als Koordinaten eines Punktes aufgefaßt werden, der sich in Abh¨angigkeit von der Zeit durch den Phasenraum bewegt. Die Bahn eines solchen Punktes ist eine Trajektorie, f¨ur die die Aussage des Satzes 1.2 gilt. Nach Satz 1.1.1, Aussage 3 k¨onnen sich zwei nicht identische Flußlinien nicht kreuzen; durch jeden Punkt des Phasenraumes kann nur eine Trajektorie gehen. Hat man f¨ur die L¨osung x(t) also einen Punkt — dieAnfangsbedingung — spezifiziert, so ist damit der Verlauf von x(t) festgelegt.
Die Funktionenvi in (1.1) k¨onnenlinearodernichtlinear sein. Sind alle Funktionen v1,· · ·, vnlinear, so heißt das Systemlinear. Lineare Systeme spielen in den Anwendungen der Systemtheorie eine zentrale Rolle, u.a. deswegen, weil sich die L¨osungen f¨ur solche Sy- steme zumindest grunds¨atzlich anschreiben lassen. Bei nichtlinearen Systemen l¨aßt sich in einfachen F¨allen x(t) explizit herleiten, in vielen F¨allen ist aber eine solche explizite Herleitung nicht nur schwierig, sondern unn¨oglich: gem¨aß einem Satz von Liouville exi- stieren vielfach gar keine geschlossenen Ausdr¨ucke f¨urx(t), und wenn sie existieren, sind sie nicht notwendig auch hilfreich, um das Verhalten des Systems zu erfassen (Arnol’d (1980), p. 39). Nun sind die meisten biologischen Systeme, insbesondere auch das visuel- le System, nichtlinear. Gleichwohl ist der eben genannte Sachverhalt, dass sich n¨amlich nur selten die L¨osungen in expliziter Form angeben lassen, kein Grund zur Melancholie.
Denn f¨ur eine große Klasse nichtlinearer Systeme lassen sichLinearisierungen angeben, die das Verhalten des Systems f¨ur kleine Auslenkungen, d.h. f¨ur St¨orungen mit geringer Intensit¨at, im Rahmen der Theorie linearer Systeme zu beschreiben gestatten. Zumindest im Prinzip ist es auch m¨oglich, von den linearisierten Versionen auf die Nichtlinearit¨aten zu schließen. Im Folgenden sollen deshalb die linearen Systeme ausf¨uhrlicher dargestellt werden; Bedingungen f¨ur die Linearisierbarkeit eines nichtlinearen Systems werden im Anschluß daran angegeben.
1.2 Lineare Systeme
1.2.1 Allgemeine Charakterisierung
Es sei ˙x=v(x) ein System von Dgln. Dann sindxundx n-dimensionale Vektoren, undv kann kann abstrakt als Abbildungv:Rn→Rn verstanden werden. Istvlinear, so heißt
˙
x=v(x) einlineares Systemmit der Dimensionn. Dann kann das System in der Form
˙
x=v(x) =Ax+u (1.3)
geschrieben werden4 Dabei ist
x= (x1,· · ·, xn)′
der Zustandsvektor, die Komponentenxi=xi(t) sind nat¨urlich Funktionen der Zeit und heißen Zustandsvariablen. Diese Variablen k¨onnen direkt physikalische oder psycholo- gische Variable abbilden, sie k¨onnen aber auch bestimmte Funktionen solcher Variablen
4Die Bezeichnunglineares Systemist ¨ublich, wenn auch ein wenig lax, denn linear (im mathematischen Sinne) ist es nur f¨ur den Fallu≡0. (1.3) heißt eigentlichaffines System.
sein; auf spezielle Interpretationen wird sp¨ater eingegangen.Aist dieKoeffizientenmatrix
A=
a11 a12 · · · a1n
a21 a22 · · · a2n
... an1 an2 · · · ann
Die aij k¨onnen Funktionen der Zeit sein, sie k¨onnen aber auch Konstante sein; im letzteren Fall handelt es sich bei (1.3) um ein System mit konstanten Koeffizienten;
die folgenden Betrachtungen gelten f¨ur beide Arten von Systemen. Der Vektor u = (u1(t),· · ·, un(t))′ repr¨asentiert ”St¨orungen” des Systems. F¨ur die i-te Komponente des Vektorsxgilt dann jedenfalls
˙
xi(t) = dXi(t) dt =
Xn
j=1
aijx1(t), i= 1,· · ·, n. (1.4) F¨uru(t)≡0 im betrachteten Zeitintervall ergibt sich
˙
x=Ax; (1.5)
diese Gleichung beschreibt ein homogenes System. Ein homogenes System bewegt sich nicht unter dem Einfluß einer ¨außeren ”St¨orung”. F¨ur den Spezialfall ˙x= 0 findet keine Zustands¨anderung statt, d.h. das System f¨uhrt keinerlei Bewegung aus. Das System ist dann in einerGleichgewichtslageoder in einemFixpunkt. Die Menge der Fixpunkte errgibt sich aus der Diskussion der Gleichung
Ax= 0 (1.6)
Ist der Rang von Agleich n, d.h. istdetA=|A| 6= 0, so weiß man aus der Theorie der linearen Gleichungssysteme, dass es f¨ur (1.6) nur eine L¨osung gibt, n¨amlich x= 0 f¨ur allet. Ist dagegen|A|= 0, d.h. ist der Rang vonAkleiner alsn, so sind die Gleichungen (1.6) voneinander abh¨angig und es exisitiert eine Hyperebene, auf der (1.6) erf¨ullt ist.
Eine ausf¨uhrliche Diskussion dieses Falles kann hier ni Knobloch & Kappel (1974)). Es gen¨ugt hier, sich auf den Fall |A| 6= 0 zu beschr¨anken. Die Gleichungen in (1.6) sind dann voneinander unabh¨angig und stellen insofern eine ¨okonomische Beschreibung des Systems dar; da das Ziel psychophysischer Untersuchungen eine Beschreibung des visuel- len Systems oder Teilen davon ist, wird man immer auf eine ¨okonomische Beschreibung abzielen.
Es sei also|A| 6= 0 und es seit0 der Anfangspunkt des Intervalles, in demu(t)≡0 gilt, und es seix0=x(t0). Istx06= 0, so ist das Systemausgelenkt, d.h. es ist durch eine vorangehende St¨orung aus der Gleichgewichtslage in den Zustand x0 gebracht worden.
Man hat etwa durch einen Stoß die Stimmgabel in Schwingungen versetzt, oder die Spiralfeder zu einem gewissen Gerade zusammengedr¨uckt oder auseinander gezogen. Die Stimmgabel wird irgendwann schwingen, sie strebt dem Fixpunkt x= 0 zu. Die innere Reibung in der Gabel bedeutet, dass die Schwingungen ged¨ampft werden, bis eben keine Schwingung mehr vorhanden ist. F¨ur ein beliebiges System kann es sein, dass es, vont0an sich selbst ¨uberlassen, nicht gegen einen Fixpunkt strebt: einige oder alle Komponenten vonxk¨onnen gegen Unendlich streben, oder das System schwingt ohne jede D¨ampfung.
Strebt x gegen einen Fixpunkt, so ist das System stabil nstabil. Es zeigt sich, dass es von den Eigenwerten vonAabh¨angt, ob ein System stabil ist oder nicht; hierauf wird in Abschnitt 1.2.7 n¨aher eingegangen.
Bei den in diesem Buch behandelten Systemen handelt es sich um Informations¨uber- tragungssysteme. Dementsprechend kann der Vektoruauch als Vektor vonEingangssi- gnalenoder alsInput-Vektoraufgefaßt werden. Unter bestimmten Bedingungen sind dann die Komponenten des Vektorsxdie Ausgangssignale. Es wird sich aber oft als n¨utzlich erweisen, die Ausgangssignale als eine bestimmte Transformation des Vektors aufzufas- sen. So seiCeinem×n-Matrix undy= (y1,· · ·, ym)′ sei einc-dimensionaler Vektor, der die Ausgangssignale repr¨asentieren m¨oge. Außerdem kann man noch zulassen, dass der Eingangsvektorueine direkte Wirkung aufy haben darf. Dazu seiDeinem×n-Matrix, und der Ausgangsvektor sei durchCx+Dudefiniert. Außerdem k¨onnen wir noch zulas- sen, dass der Vektor u in transformierter Form auf den Zustand des Systems einwirkt, d.h. in der FormBu. Das System (1.3) kann dann in der Form
˙
x = Ax+Bu (1.7)
y = Cx+Du
angeschrieben werden. Die MatrixB heißt auchKontrollmatrix,C heißtOutput-Matrix, undD heißtFeedforward-Matrix.y heißtOutput-Vektor.
Das visuelle System ist wie die meisten biologischen Systeme nichtlinear. Die Bedeu- tung der linearen Systeme ergibt sich aus dem Umstand, dass einerseits lineare Systeme einer mathematischen Analyse leichter zug¨anglich sind und nichtlineare Systeme f¨ur klei- ne Auslenkungen, d.h. St¨orungen, h¨aufig durch lineare Systeme in sehr guter N¨aherung beschrieben werden k¨onnen. Die Linearisierung nichtlinearer Systeme setzt die Kennt- nis einer Reihe von Eigenschaften linearer Systeme voraus, weshalb lineare Systeme in einiger Ausf¨uhrlichkeit behandelt werden sollen.
Die Gleichung (1.3) ergibt sich direkt aus der Definition des Begriffes Dynamisches System. Dies bedeutet, dass sichjedes lineare System in der Form (1.3) darstellen l¨aßt.
Deshalb heißt das System von Dgln (1.3) bzw. (1.7) auch dieNormalform.
1.2.2 Die L¨ osungen eines linearen Systems 1.2.3 Die Exponentialmatrix
Zur Vorbereitung wird der Begriff der Exponentialmatrix eingef¨uhrt. Es sei zun¨achst daran erinnert, dass eine hinreichend oft differenzierbare Funktion f(x) in eine Taylor- Reihe entwickelt werden kann
f(x) =f(0) + x
1!f(1)(0) +x2
2!f(2)(0) +x3
3!f(3)(0) +· · · (1.8) Dabei ist
f(n)(x) = dn
dxf(x), n= 1,2,· · ·
dien-te Ableitung vonf an der Stellex;f(n)(0) ist also dien-te Ableitung vonf an der Stellex= 0. Setzt manξ=x+h, so kann manf in eine Taylor-Reihe um den Punktx
entwickeln:
f(ξ) =f(x+h) =f(x) + h
1!f(1)(x) +h2
2!f(2)(x) +h3
3!f(3)(x) +· · · (1.9) F¨ur hinreichend kleine Werte vonhkann alsof durch einelineare Funktion
f(x+h)≈f(x) +hf′(x), f′(x) = df(x) dx
angen¨ahert werden; es ist jah/1! =h.f′(x) ist die Steigung,f(x) ist die additive Kon- stante bei dieser Approximation. Auf diese Approximation wird bei der Linearisierung nichtlinearer Systeme zur¨uckgegriffen.
Es sei nunPeinen×n-Matrix. Dann istP2=P·P,P3=P·P·P, etc. Weiter seiaein Skalar, d.h. eine reelle Zahl (d.h. a∈R). Dann istaP eine Matrix, deren Elemente sich von den Elementen der MatrixP durch die Multiplikation mit der Zahlaunterscheiden.
Ist alsopij das Element in deri-ten Zeile undj-ten Spalte vonP, so istapij das Element in deri-ten Zeile undj-ten Spalte vonaP. Man kann dann die unendliche R eihe
P0 0! +P1
1! +P2
2! +· · ·= X∞
k=0
Pk
k! (1.10)
bilden. Dabei ist P0 eine Matrix, deren Elemente alle gleich 1 sind, und da 0! = 1, ist P0/0! eine Matrix, deren Elemente alle gleich 1 sind. Der Faktor 1/k! ist eine reelle Zahl, so dass Pk/k! eine Matrix ist, deren Elemente dadurch entstehen, dass zun¨achst P k-mal mit sich selbst multipliziert wird und dann die Elemente vonPk mit a= 1/k!
mmultipliziert werden.
Die Reihe (1.10) entsprichtformalder Taylor-Reihe f¨ur die Funktionf(x) =ex, d.h.
ex= 1 +x1 1! +x2
2! +x3
3! +· · ·= X∞
k=0
xk k!
Wegen der Analogie zu der in (1.10) eingef¨uhrten Reihe wird man zu der folgenden Definition gef¨uhrt:
Definition 1.2.1 Die Matrix
H= X∞
k=0
Pk
k! =:eP (1.11)
heißt Exponentialmatrix5.
Ein im folgenden Abschnitt interessierender Spezialfall ist die Exponentialmatrix der MatrixAt; es gilt
eAt= X∞
k=0
(At)k
k! (1.12)
5Das Zeichen ”=:” soll heißen, dass das SymboleP durch die links stehende Summe definiert wird.
und
e−At= X∞
k=0
(−At)k k! =
X∞
k=0
(−1)k(At)k
k! (1.13)
F¨ur sp¨atere Anwendungen sei gleich noch der Ausdruck f¨ur die Ableitung voneA bzw.
e−Atnachtangef¨ugt: es ist d
dteAt = d
dt(1 +At+(At)2
2! +(At)3 3! +· · ·)
= A+2(At)A
2! +3(At)2A
3! +4(At)3A 4! +· · ·
= (1 +At+(At)2
2! +(At)3
3! +· · ·)A
= eAtA (1.14)
Andererseits gilt f¨ur die Terme (At)k−1A/(k−1)!
k(At)k−1A
k! = (At)k−1A
(k−1)! = Aktk−1
(k−1)! =A(At)k−1 (k−1)!, denntist ja ein Skalar, d.h. es gilttA=At, so dass man auch
d
dteAt=AeAt (1.15)
schreiben kann. Auf analoge Weise zeigt man, dass d
dte−At=−Ae−At (1.16)
ist.
Herleitung der L¨osung
Es wird zun¨achst das homogene System ˙x=Axbetrachtet. Es gilt der
Satz 1.2.1 Es seiA eine konstante Matrix, d.h. die Elementeaij der Matrix A sollen nicht von der Zeit abh¨angen. Dann istx(t)durch
x(t) =x0eAt (1.17)
gegeben.
Beweis: Eine M¨oglichkeit, die L¨osung f¨ur das homogene System herzuleiten, besteht darin, den L¨osungsvektorx(t) in eine Taylor- bzw. MacLaurin-Reihe zu entwickeln; dies bedeutet, dass jede Komponente vonxin eine solche Reihe entwickelt wird. Mitx0=x(0) soll also gelten
x(t) = x0+t x(1)(0) + +t2
2!x(2)(0) +t3
3!x(3)(0) +· · · (1.18)
Dabei ist wieder
x(k)(0) = dk dtx(t)
t=0
, k= 1,2,· · ·
Nun ist x(1)0 =AX0, x(2)0 =Ax(1)0 =A2x0, x(3)0 =Ax(2)0 = A3x0, etc. Setzt man diese Ausdr¨ucke in (1.18) ein, so erh¨alt man die Reihe
x(t) =x0(1 +tA+t2
2!A2+t3
3!A3+· · ·) =x0(1 +At+(At)2
2! +(At)3
3! +· · ·), (1.19) denntA=At. In der Klammer rechts steht aber gerade die Exponentialmatrix vonAt,
so dass man (1.17) erh¨alt.
Jetzt kann die L¨osung f¨ur das inhomogene System ˙x=Ax+ubestimmt werden. Es gilt Satz 1.2.2 Gegeben sei das inhomogene Gleichungssystemx˙ =Ax+usowie einen Vek- tor x0 von Anfangswerten. Dann sind die L¨osungen x(t)f¨ur dieses System durch
x(t) =xc(t) +xp(t). (1.20) gegeben. Dabei ist
xc(t) =eA(t−t0)x0, xp(t) = Z t
t0
eA(t−τ)u(τ)dτ. (1.21) mitx0=x(t0).
Beweis: Die Gleichung ˙x = Ax+u impliziert ˙x−Ax = u. Multipliziert man diese Gleichung von links mite−At, so erh¨alt man
e−Atx˙−e−AtAx=e−Atu
Sindf undgirgendzwei Funktionen vont, so ist die Ableitung des Produktsf gnach der Produktregel durch (f g)′ =f′g+f g′ gegeben. Die vorangehende Gleichung legt nahe, dass sie ¨uber die Ableitung eines Produktes beschrieben werden kann. Es werde dazu die Ableitung des Produktse−Atxbetrachtet; es ist
d
dt(eAtx) =e−Atx˙−Ae−Atx=e−At( ˙x−Ax) =e−Atu.
Integration bez¨uglichtliefert Z d
dt(eAtx)dt=eAtx(t) = Z
eAtu(t)dt.
Integriert man f¨ur die Grenzent0(= Anfangszeitpunkt) undt, so erh¨alt man insbesondere Z t
t0
d
dt(eAτx)dτ =eAtx(t)−eAt0x(t0) = Z t
t0
eAτu(τ)d τ
oder
eAtx(t) =eAt0x(t0) + Z t
t0
eAτu(τ)d τ Multiplikation dieser Gleichung mit e−Atliefert dann
x(t) =e−A(t−t0)x(t0) + Z t
t0
e−A(t−τ)u(τ)dτ (1.22)
und dies ist gerade (1.20).
Abbildung 1.1: Komplement¨are, partikul¨are und Gesamtantwort auf eine Schrittfunktion
0 2 4 6 8 10
0,0 0,5 1,0 1,5 2,0
Systemantwort
t
partikuläre Lösung komplementäre Lösung Gesamtantwort
Bemerkungen:
1. Allgemein setzt sich die L¨osung der linearen (affinen) Differentialgleichung aus zwei Teill¨osungen zusammen:
• xc(t), diekomplement¨are L¨osung
• xp(t), diepartikul¨are L¨osung
2. Der komplement¨are Teil xc der L¨osung h¨angt von der ”Auslenkung” des Systems zur Zeit t0 ab, zu dem der Input (die ”St¨orung”) des Systems durch u beginnt, w¨ahrendxp nur durch den Inputubestimmt wird.
3. Die Art der Reaktion des Systems h¨angt offenbar von der ExponentialmatrixH(t) :=
eAtab. IstH bekannt, l¨aßt sich die Reaktion des Systems auf einen beliebigen In- put u berechnen. Um H weiter zu spezifizieren, wird im folgenden Teilabschnitt ein spezieller Inputubetrachtet, der f¨ur die experimentelle Charakterisierung der MatrixH(t) =eAtund damit des Systems von Bedeutung ist.
Beispiel 1.2.1 Es sein= 1 und das Eingangssignal sei eine Schrittfunktion, d.h. es sei u(t) =
0, t≤0
1, t >0 (1.23)
F¨urn= 1 ist A=a,a∈Reine einzelne reelle Zahl. Die Anwendung von (1.22) liefert, wenn man der Einfachheitt0= 0 annimmt,
x(t) =x(0)e−at+ Z t
0
e−a(t−τ)dτ (1.24)
Es ist aber Z t
0
e−a(t−τ)dτ =e−at Z t
0
eaτdτ =e−at1
a eat−1
=1
a 1−e−at , so dass sich schließlich
x(t) =x(0)e−at−1
a 1−e−at
(1.25)
ergibt. F¨ur x(0) = 0 befindet sich das System in der Ruhelage, f¨ur x(0) 6= 0 ist das System bereits aus der Ruhelage ausgelenkt, wenn die St¨orung durchu(t) beginnt.
Man muß jetzt zwei F¨alle betrachten: (i)a <0 und (ii) a >0. F¨ur den Fallx(0)6= 0 strebt die komplement¨are L¨osungx(0)e−at gegen Null, wenna >0, und die partikul¨are L¨osung strebt gegen 1/a. F¨ura >0 strebt also die Antwort des Systems gegen die Kon- stante 1/a; das System iststabil. F¨ur den Falla <0 w¨achste−atallerdings unbeschr¨ankt;
das System istinstabil. Der logisch m¨ogliche Falla= 0 ist aus offensichtlichen Gr¨unden uninteressant.
1.2.4 Die Dirac-Impuls-Funktion und die Impulsantwort-Matrix
Definition 1.2.2 Die Funktionδ:R→Rsei durch die folgenden Bedingungen charak- terisiert:
1.
δ(ξ) =
∞. ξ= 0 0, ξ6= 0
(1.26)
2. Z ∞
−∞
δ(ξ)dξ = 1 (1.27)
3. Es seif eine beliebige Funktion. Dann gilt Z ∞
−∞
f(ξ)δ(x−ξ)dτ =f(x) (1.28)
Dann heißtδ Dirac-Delta-FunktionoderDirac-Impuls6.
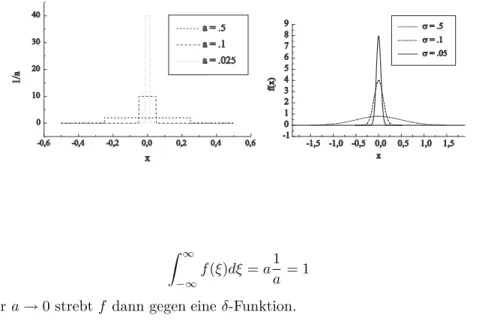
Die δ-Funktion hat auf den ersten Blick bizarre Eigenschaften: sie ist nur f¨ur x = 0 von Null verschieden; f¨ur x = 0 nimmt sie den Wert ∞ an, und das Integral ¨uber δ soll den endlichen Wert 1 haben. In der Tat ist die δ-Funktion keine gew¨ohnliche Funktion, sondern eine verallgemeinerte Funktion. Man kann sich ihre Definition aber veranschaulichen.
Beispiel 1.2.2 Dazu betrachte man die Funktion
f(ξ) =
0, x <−a/2 1/a, −a/2≤ξ≤a/2 0, ξ > a/2
f definiert offenbar ein Rechteck der Breiteaund der H¨ohe 1/a, so dass f¨ur allea6= 0
6Nach ihrem Erfinder, dem Physiker Paul Adrien Maurice Dirac, (1902 – 1984), Mathematiker, we- sentliche Leistungen in der Quantenmechanik.
Abbildung 1.2: Approximation der Dirac-Funktion: Rechteckpulse und Gauß-Funktionen
-0,6 -0,4 -0,2 0,0 0,2 0,4 0,6
0 10 20 30 40
a = .5 a = .1 a = .025
1/a
x
-1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 -1
0 1 2 3 4 5 6 7 8 9
f(x)
x
σ = .5 σ = .1 σ = .05
Z ∞
−∞
f(ξ)dξ=a1 a = 1
gilt. F¨ura→0 strebtf dann gegen eineδ-Funktion.
Beispiel 1.2.3 Die Gaußfunktion f(ξ) = 1
σ√ 2πexp
− ξ2 2σ2
ist ein weiteres Beispiel. Sicherlich ist das Integral ¨uber f gleich 1 (f ist ja eine Dichte- funktion), und f¨urσ→0 strebtf gegen eineδ-Funktion.
Die Bedingung (1.28) ist intuitiv einleuchtend:δnimmt ja nur dann einen von Null verschiedenen Wert an, wenn das Argument ξ gleich Null ist. Dies ist der Fall, wenn ξ=xist. Gleichwohl ist die Forderung (1.28) nicht trivial, denn f¨ur diesen Fall ist jaδ gleich unendlich! dass sie Sinn macht, kann man anhand der in den Beispielen 1.2.2 und 1.2.3 betrachteten Funktionen ¨uberpr¨ufen, wenn man a bzw.σ na egration gegen Null gehen l¨aßt.
W¨ahlt man nun f¨ur u einen Vektor, dessen Komponenten aus δ-Funktionen δ(τ) bestehen, so liefert insbesondere (1.28) die Beziehung
Z ∞
−∞
eA(t−τ)u(τ)dτ =eAt (1.29) Dementsprechend heißtH(t) =eAt auch dieImpulsantwortmatrix.
Das System ist durch die MatrixAder Kopplungskoeffizienten bestimmt. Die Impul- santwortmatrixHist wiederum durchAbestimmt. Gibt man nun einen Impuls (im Sinne derδ-Funktion) auf das System, so ist die Antwort gerade durchH(t) gegeben. Gelingt es,H(t) aus der Beobachtung abzusch¨atzen und kannAausH berechnet werden, so hat man damit das System identifiziert. Auf die tats¨achliche Durchf¨uhrung dieses Ansatzes wird sp¨ater zur¨uckgekommen.
1.2.5 Die Operator-Schreibweise
Der lineare Operator und das Superpositionsprinzip F¨ur die hier verfolgten Zwecke kann man sagen, da0 ein System f¨uhrt ein Inputsignal in eine Antwort bzw.
in ein Outputsignal ¨uberf¨uhrt, Dies l¨aßt sich durch die Operatorschreibweise ausdr¨ucken.
Dabei wird das System durch denOperatorL repr¨asentiert; es gilt
L(u) =x (1.30)
wobei u und x nat¨urlich (vektorielle) Funktionen etwa von t sind, also u = u(t) und x=x(t). Man zeigt nun leicht die G¨ultigkeit von
Satz 1.2.3 Der OperatorL(bzw. dass durch den OperatorLrepr¨asentierte System) sei linear. Dann gilt
L(α1u1+α2u2) =α1x1+α2x2 (1.31) wennL(u1) =x1 undL(u2) =x2.
Beweis:Aus ˙xi=Axi+ui,i= 1,2 folgtui= ˙xi−Axi und damitαiui=αix˙i−αiAxi
und sicherlich
α1u1+α2u2=α1x˙1+α2x˙2−α1Ax1−α2Ax2=α1x˙1+α2x˙2−A(α1x1+α2x2) bzw.
α1x˙1+α2x˙2=A(α1x1+α2x2) +α1u1+α2u2
und dies ist gerade die Aussage des Satzes: man muß nur x=α1x1+α2x2setzen.
Bemerkungen:
1. Die Aussage (1.31) heißt auchSuperpositionsprinzip.
2. Das Superpositionsprinzip kann auch zur Definition von linearen Systemen gew¨ahlt werden. W¨ahrend das Superpositionsprinzip allerdings leicht aus der linearen Dif- ferentialgleichung ˙x=Ax+ufolgt, ist es schwieriger, die Differentialgleichung aus dem Superpositionsprinzip herzuleiten. Deshalb wurden hier lineare Systeme durch die linearen Differentialgleichungen definiert.
Die Impulsantwort und die Darstellung vonxals FaltungsintegralEs sei ∆(t) = (δ1(t), δ2(t),· · ·, δn(t))′ und das Inputsignal sei durch ∆ definiert, d.h. es m¨ogeu(t) =
∆(t) gelten. Dann kann man
L(u) =L(∆) =H(t) (1.32)
schreiben; die Antwort des Systems ist gerade die Impulsantwort. Man bemerke, dass die Impulsantwort des Systems durch (1.32) auch definiertwerden kann; w¨ahlt man diesen Weg, hat man allerdings die Aufgabe, zu zeigen, dassH gerade die FormeAthat.
Der Nutzen von (1.32) besteht andererseits u.a. darin, dass Eingangs- und Ausgangs- signal stets durch eineFaltungaufeinander bezogen sind:
Definition 1.2.3 Es seien f und hirgendzwei Funktionen. Dann heißt das Integral x(t) =
Z ∞
−∞
f(τ)h(t−τ)dτ (1.33)
einFaltungsintegraloder einfach Faltungvonf undh. Man schreibt auch abk¨urzend
x=f∗h (1.34)
Nach Satz 1.2.2, p. 15, ist die partikul¨are L¨osung der Gleichung ˙x=Ax+u, d.h. der Teil der L¨osung, der durch den Inputu”erzwungen” wird, durch
xp(t) = Z t
t0
e−A(t−τ)u(τ)dτ
gegeben. Das Integral auf der rechten Seite hat die Form einer Faltung, auch wenn e−A(t−τ)u(τ) ein Vektor ist. Generell gilt der folgende Satz:
Satz 1.2.4 Gilt die Beziehung (1.33), so gilt auch x(t) =
Z ∞
−∞
f(t−τ)h(τ)dτ (1.35)
Beweis: Der Beweis erfolgt durch Substitution vonξ=t−τ und nachfolgende Umbe-
nennung der Variablen.
Der Ausdruck (1.29) f¨ur xp ist eine Vektorgleichung. Ihre Struktur wird deutlicher, wenn man sie etwas ausf¨uhrlicher anschreibt. Es seien hij(t) die Elemente der Matrix H(t) =eAt. Diei-te Komponente des VektorseA(t−τ)u(τ) ist dann durch das Skalarpro- dukt deri-ten Zeile voneA(t−τ)mit dem Vektor u(τ) gegeben, d.h. durch
hi1(t−τ)u(τ) +· · ·hin(t−τ)unn(τ) = Xn
j=1
hij(t−τ)uj(τ),
ujdiej-te Komponente vonu, und diei-te Komponente des Antwortvektorsxipist durch xip(t) =
Z t t0
Xn
j=1
hij(t−τ)u(τ)dτ = Xn
j=1
Z t t0
hij(t−τ)u(τ)dτ (1.36) gegeben (Vertauschbarkeit von Summation und Integration vorausgesetzt). Man sieht, dass die Komponenten des Antwortvektors durch eine Summe von einfachen (nicht vek- toriellen) Faltungsintegralen gegeben sind. Sind die Komponenten von u insbesondere δ-Funktionen, so erh¨alt man
xip(t) = Xn
j=1
Z t t0
hij(t−τ)δ(τ)dτ = Xn
j=1
hij(t). (1.37)
Beispiel 1.2.4 Ein besonders einfaches Beispiel ist der Fall n = 1. Das System ˙x = Ax+ugeht dann in das System ˙x=ax+uuber, wobei¨ a∈R, denn die MatrixA hat jetzt nur ein Element, n¨amlich a. Die Impulsantwort des Systems ist dann
H(t) =ceat, a∈R, c∈R (1.38) wobei ceine Proportionalit¨atskonstante ist. Statt (1.38) kann dann auch
L[δ(t)] =c Z t
0
ea(t−τ)δ(τ)dτ =ceat
geschrieben werden. F¨ura >0 w¨achst die Antwort als Reaktion auf den Impuls offenbar unbeschr¨ankt (zumindest so lange, wie die Rahmenbedingungen, unter denen das System definiert ist, gelten); das System ist instabil. F¨ur a < 0 f¨allt die Antwort von ihrem Maximumc exponentiell gegen Null ab (das Systemrelaxiert); das System iststabil.
Die in Beispiel 1.38 angesprochene Frage der Stabilit¨at eines linearen Systems kann nur diskutiert werden, wenn bekannt ist, wieH(t) =eAtim allgemeinen Falln >1 berechnet wird. Darauf wird im folgenden Abschnitt eingegangen.
1.2.6 Zur Berechnung der Impulsmatrix
A ist eine n×n-Matrix. Es sei T eine n×n-Matrix, f¨ur die die inverse Matrix T−1 existieren m¨oge, so dassT T−1=T−1T =I,Idie Einheitsmatrix. Weiter seiT−1AT = Λ, Λ wieder einen×n-Matrix, so dassA=TΛT−1. Insbesondere sei Λ die Diagonalmatrix der Eigenwerte von A, wobei vorausgesetzt werde, dass alle Eigenwerte vonAverschieden seien. Die MatrixT enth¨alt dann die Eigenvektoren vonA. Ist ein Eigenwertλikomplex, so dassλi =λi1+jλi2 mit j =√
−1 gilt, so existiert stets ein zweiter Eigenwertλk = λ¯i=λi1−jλi2und die zugeh¨origen Eigenvektoren sind ebenfalls konjugiert komplex (f¨ur eine Begr¨undung dieser Aussage lese man in Lehrb¨uchern der linearen Algebra nach). Es gilt nun der
Satz 1.2.5 Es sei T die Matrix der Eigenvektoren von A, und Λ sei die zugeh¨orige Diagonalmatrix der Eigenwerte vonA. Dann gilt
eAt=T eΛtT−1, (1.39)
wobei
eΛt=
eλ1t 0 · · · 0 0 eλ2t · · · 0 ... ... ... ... 0 0 · · · eλnt
(1.40)
ist.
Beweis: Aus T−1AT = Λ folgt sofort A = TΛT−1. Weiter ist A2 = (TΛT−1)2 = TΛT−1TΛT−1 =TΛ2T−1, A3 =A2A =TΛ2T−1TΛT−1=TΛ3T−1, etc, so dass man allgemein
Ak=TΛkT−1 (1.41)
folgern kann. Analog zeigt man, dass
(At)k =T(Λt)kT−1 (1.42)
Es ist aber eAt=
X∞
k=0
(At)k k! =
X∞
k=0
T(λt)kT−1 k! =T
X∞
k=0
(λt)k k!
!
T−1=T eΛtT−1
womit (1.39) gezeigt ist.
(1.39) zeigt, dass man zur Berechnung von eAt nicht alle Terme (At)k/k! der un- endlichen Reihe (1.12 ) berechnen muß. Es gen¨ugt vielmehr, die Eigenwerte und die zugeh¨origen Eigenvektoren der Matrix Azu berechnen, umeAt f¨ur allet bestimmen zu k¨onnen.
Insbesondere kann man nun einen expliziten Ausdruck f¨ur die Elemente hij(t) der Impulsantwortmatrix angeben. Es seitij das Element in deri-ten Reihe undj-ten Spalte von T (d.h.tij sei die i-te Komponente des j-ten Eigenvektors vonA), und ˜tij sei das entsprechende Element vonT−1. Dann gilt wegenH =eAt=T eΛtT−1
hij(t) = Xn
k=1
tik˜tkjeλkt˜tkj = Xn
k=1
tik˜tkjeλkt (1.43) Das Element hij ist also eine Summe von Exponentialfunktioneneλkt, ”gewichtet” mit dentik˜tkj. Auf die inhaltliche Bedeutung dieses Sachverhalts wird eingegangen, wenn die verschiedenen Formen der Zusammenschaltung von Systemen diskutiert wird.
1.2.7 Stabilit¨ at linearer Systeme; Eigenfrequenzen
Nach (1.37) ist nunxpi(t) =P
jhij(t), und damit ist xpi(t) =
Xn
j=1
Xn
k=1
tik˜tkjeλkt= Xn
k=1
Xn
j=1
tikt˜kj
eλkt= Xn
k=1
cikeλkt (1.44)
mit cik = P
jtik˜tkj. Die i-te Komponente der Reaktion auf einen Impuls ist also eine Summe von Exponentialfunktionen. Hieraus wird sofort die Bedeutung der Eigenwerte von Adeutlich. So seiλk ∈Rund weiter gelteλk >0. Dann w¨achsteλktunbeschr¨ankt und damit auch xpi(t), d.h. das System istinstabil. Es sei weiterλk ∈C, wobei mitC die Menge der komplexen Zahlen bezeichnet wird, so dassλk=αk+iβk. Dann existiert stets ein Eigenwertλs= ¯λk =αk−i βk und die Koeffizientencik undcissind ebenfalls zueinander konjugiert komplex, d.h.cis = ¯cik =|cik|e−iφ, ¯cik =|cik|eiφ, so dass wir f¨ur diese beiden Eigenwerte die Teilsumme
Sik(t) :=|cik|eiφeλkt+|cik|e−iφe¯λkt=|cik|eαkt
ei(βkt+φ)+e−i(βkt+φ) d.h.
Sik(t) =|cik|eiφeλkt+|cik|e−iφe¯λkt= 2eαkt|cik|cos(βkt+φ). (1.45)
Die Existenz eines Paares konjugiert komplexer Eigenwerte bedeutet also, dass die ent- sprechende Komponente der Impulsantwort mit der Frequenz βk schwingt; dies ist eine Eigenschwingungdes Systems, undβk heißt dementsprechend eineEigenfrequenzdes Sy- stems. Gibt es mehrere Paare von Eigenwerten, so gibt es verschiedene Eigenfrequenzen und damit verschiedene Eigenschwingungen, die sich additiv ¨uberlagern.
Aus (1.45) folgt sofort eine Aussage ¨uber die Stabilit¨at von linearen Systemen. F¨ur
|cik|<∞ist auch|cik|cos(βkt+φ)<∞f¨ur allet. Σik(t) h¨angt allerdings noch von dem Faktor eαkt ab. αk ist der Realteil des Eigenwerts λk. F¨ur αk >0 strebt dieser Faktor gegen unendlich, damit auch Σik(t) und damit die Systemantwort insgesamt: das System ist instabil. F¨urαk<0 gegen Null, und damitSik(t). Damit gilt
Satz 1.2.6 Das System x˙ = Ax+u ist stabil, wenn die Realteile aller Eigenwerte λk
von Anegativ sind.
Definition 1.2.4 Die Funktionenexp(λjt)heißen dieModendes Systems, und die Vek- toren eλjtTj heißen diedynamischen Moden des Systems. Die Matrix derT der Eigen- vektoren heißt auchModalmatrix.
1.2.8 Anmerkungen zum Zustandsbegriff
F¨ur das System ˙x=Ax+u- die folgenden Betrachtungen ¨ubertragen sich auf das verall- gemeinerte System (1.7) - waren die Komponenten des Vektorsxals Zustandsvariablen bezeichnet worden. Die Definition des Zustands eines linearen Systems ist aber nicht ein- deutig. So sei etwaT einen×nMatrix mit konstanten Koeffizienten, f¨ur die die Inverse T−1 existieren m¨oge (T sei also nichtsingul¨ar). Ist x nun ein Zustandsvektor, so kann man durch die TransformationT−1xzu einem neuen n-dimensionalen Vektorz =z(t) ubergehen. F¨ur jeden Zeitpunkt¨ t korrespondiert dann zu xder Vektorz. Multipliziert man von links mit T, so erh¨alt man T T−1x=x=T z, so dass man auch sagen kann, der Vektor xsei durch Transformation aus einem Vektor z hervorgegangen. Da T eine Matrix mit konstanten Elementen ist, folgt ˙x=Tz, und die Gleichung˙
˙
x=Ax+u kann dann in der Form
Tz˙ =AT z+u
geschrieben werden. Multipliziert man nun von links mitT−1, so erh¨alt man die Gleichung
˙
z=T−1AT z+T−1u. (1.46)
F¨ur den Zustandsvektor z wird das System, d.h. werden die Kopplungen zwischen den Zustandsvariablen, also durch die MatrixT−1ATund nicht mehr durch die MatrixAcha- rakterisiert. Nat¨urlich ergibt sich jetzt die Frage, welche Aspekte der Systembeschreibung denn invariant sind, wenn schon die Definition der Zustandsvariablen nicht eindeutig ist.
Es zeigt sich, dass die Eigenwerte vonA und T−1AT die gleichen sind. Die Eigenwerte von A ergeben sich als Wurzeln des Polynoms Q(λ) = |A−λI| = 0. F¨ur die Matrix T−1AT hat man f¨ur die Eigenwerte ein Polynom ˜Q(µ) =|T−1AT −µI| = 0. Nun gilt aberI =T−1T, so dass man auch ˜Q(µ) =|T−1AT−µT−1T|= 0 schreiben kann. Dies
ist identisch mit ˜Q(µ) = |T−1(AT −µT)| = |T−1(A−µI)T|. Aus der Matrixalgebra ist aber bekannt, dass die Determinante eines Produktes von Matrizen gleich dem Pro- dukt der entsprechenden Determinanten ist, also folgt ˜Q(µ) = |T−1||A−µI||T| = 0.
Die Determinanten|T−1|und|T|sind nach Voraussetzung ungleich Null, sonst w¨are die MatrixT nicht nichtsingul¨ar. Also muß|A−µI|= 0 gelten, d.h. aber |A−µI|=Q(µ), so dass die Eigenwerteµvon T−1AT gerade gleich den Eigenwertenλvon Asein m¨us- sen. Die Eigenwerte vonAoderT−1AT beschreiben aber gerade die qualitativ wichtigen Aspekte der Dynamik des Systems, wie etwa Stabilit¨at in Gleichgewichtslagen und die Eigenfrequenzen f¨ur den Fall komplexer Eigenwerte.
Es werde nun insbesondere angenommen, dass die Eigenwerte alle verschieden sind und dass T die Modalmatrix ist; dann gilt T−1AT = Λ = diag(λ1,· · ·, λn), und nach (1.46) erh¨alt man
˙ z=
λ1 0 · · · 0 0 λ2 · · · 0
... . ..
0 0 · · · λn
z+T−1u (1.47)
Betrachtet man als Ausgangsvariable beim urspr¨unglichen System y = Cx+Du, so ergibt sich jetzt f¨ur y die Gleichung y = ˜Cz+Du, wobei ˜C = CT ist. Das Wesent- liche an (1.47) ist aber, dass die Zustandsvariablen zi nunentkoppelt sind. Wie sp¨ater noch gezeigt werden wird, bedeutet dies, dass sich das System alsParallelschaltung be- stimmter elementarer Teilsysteme auffassen l¨aßt, weil ja die Elemente der Matrix Λ die Kopplungskoeffizienten der Zustandsvariablen enth¨alt, und hierλij = 0 f¨uri6=j ist.
Der Fall mehrerer gleicher Eigenwerte ist komplizierter und soll hier nicht einge- hend diskutiert werden; allgemein l¨aßt sich sagen, dass er sich ergibt, wenn das Sy- stem aus parallel arbeitenden Teilsystemen aufbaubar ist, die ihrerseits als r¨uckwirkungs- freie Hintereinander- oder Reihenschaltung gleichartiger Subsysteme repr¨asentiert werden k¨onnen.
1.2.9 Lineare Systeme n-ter Ordnung
Systeme der Form (1.3) bzw. (1.4), p. 1.4, sind eine allgemeine Repr¨asentation von li- nearen Systemen. Die Diskussion bestimmter dynamischer Systeme kann allerdings auf Differentialgleichungen f¨uhren, die Ableitungen h¨oherer Ordnung enthalten. Es wird die folgende Notation eingef¨uhrt: mit D werde der Differentiationsoperator bezeichnet. Ist y(t) eine mindestensn-mal differenzierbare Funktion vont, so bezeichne Dy das Differen- tial dy(t)/dt, D2y die entsprechende zweite Ableitung d2y(t)/dt2, allgemein Dny dann dien-te Ableitungdny(t)/dtn.
Beispiel 1.2.5 (Harmonischer Oszillator) Es sei ein System gegeben, das um den Betrag z(t) aus seiner Ruhelage ausgelenkt wird. Je mehr sie ausgelenkt wird, desto gr¨oßer sei die ”R¨uckstellkraft”F =F(z), mit der es in den Ausgangszustand zur¨uckzu- gelangen versucht (man denke an eine Feder). Man kann annehmen, dass diese Kraft der Auslenkung proportional ist7, und da sie der Auslenkung entgegengesetzt wirkt, kann manz(t) =−kF(z) schreiben, wobeikeine Proportionalit¨atskonstante ist. Nun ist aber
7Hookesches Gesetz