Virtual splitting of shared resource networks for pricebased coordination with portfolio tariffs

(1)

Virtual splitting of shared resource networks for price- based coordination with portfolio tariffs

Simon Wenzel

^a,*

, Lukas Samuel Maxeiner

^a

and Sebastian Engell

^a

aProcess Dynamics and Operations Group, Department of Biochemical and Chemical Engineering, TU Dortmund, Emil-Figge Straße 70, 44227 Dortmund, Germany

E-mail:{simon.wenzel;lukas.maxeiner;sebastian.engell}@tu-dortmund.de

Abstract

In the process industries the optimal allocation of shared resources among physically coupled subsystems is key to an efficient operation of the overall system, e. g., an integrated production site. If the subsystems have a certain level of autonomy or it is desired to grant confidentiality to the constituent subsystems, price-based coordination can be employed, where an independent system operator (ISO) iteratively adjusts transfer prices for the shared resources until the demand and the supply match, i. e., the shared resource networks are balanced. In this contribution, a modified subgradient price update scheme is presented, which can be used for systems that are connected to external resources, such as pipelines, through which certain amounts of the resources can be exchanged at prices that are fixed in portfolio tariffs. The approach virtually splits the shared resource networks to account for the different price regimes in the available tariff. The principle is illustrated in a simulation study of a production site with three productions plants that are connected to an external distribution grid.

Keywords: Demand-side response; Price-based coordination; Lagrangian decomposition;

Resource allocation; Resource efficiency; Energy tariffs

1. Introduction

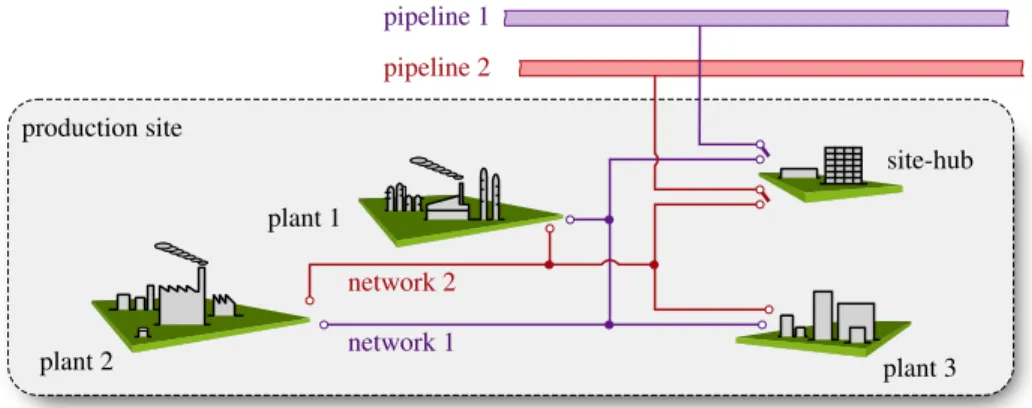
Increasing the efficiency and sustainability in the process industries is not only beneficial with respect to economic considerations, but also necessary to fulfill environmental regula- tions from the government (Siirola and Edgar, 2012). One important handle is the optimal allocation of possibly scarce and time varying shared resources such as electricity, steam at different pressure levels, heating gas, or intermediates in a system. Distributed price-based optimization techniques based on Lagrangian relaxation or ADMM (Boyd, 2010) can be used to determine the optimal allocation of shared resources in systems that consist of physically coupled subsystems, while preserving a certain level of autonomy and confidentiality (Wenzel et al., 2016). In the process industries large production sites that consist of many productions plants—possibly belonging to different business units or companies—can be regarded as such systems (Engell and Sonntag, 2016). In addition to the side-wide networks, there are usually connections to external (smart) grids (Samad and Kiliccote, 2012) as illustrated in Figure 1, through which resources can be bought or sold. This can be managed by grid tariffs that range from simple to highly sofisticated constructs (Braithwait, 2010) (e.g., see Figure 2).

Especially, when there is severe shortage or surplus of shared resources in the networks, price- based coordination algorithms lead to transfer prices that can exceed or be below the market prices of external resources by far. Thus, it is beneficial for the site to buy or sell amounts externally to overcome the shortage or surplus.

(2)

network 1 network 2

pipeline 2

plant 2 plant 3

plant 1

site-hub production site

Figure 1: Site-wide optimization problem with external pipeline connection.

In this contribution, we study such a situation and propose a price-based coordination scheme that is aware of the portfolio tariffs for the external pipeline systems or grids. The networks for the shared resources on site are virtually split according to the contract structure and the coordinating entity on site can decide to buy or sell certain amounts of shared resources. We illustrate the principle of the coordinator update in a simulation study using three production plants that are internally connected by two networks on site and externally connected to two pipelines for which a portfolio tariff with three different price regimes has been negotiated.

The rest of the paper is structured as follows: First, the site-wide optimization problem is stated. Then the modeling of the virtual networks for the price-based coordination in the presence of portfolio tariffs is introduced. A tariff-aware coordinator update is proposed and tested in a simulation study and finally a brief outlook on future research is provided.

2. Problem description

The topology of an industrial production site that consists of (partially) autonomous subsystems (plants) that are physically connected by networks for shared resources is depicted in Figure 1. The internal networks are connected to the pipelines via the site hub. The site-hub manages a surplus of demand or supply of a particular resource by buying or selling resources.

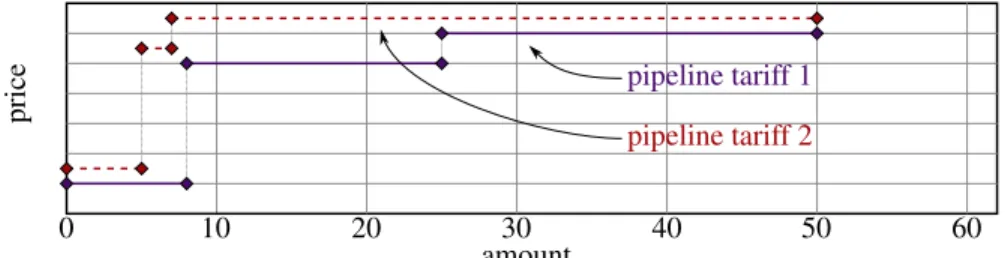
This resource allocation in the presence of different price regimes can be formulated as an optimization problem. It is assumed that the site-hub can acquire limited amounts of shared resources at different rates. A possible tariff structure that reflects the amounts and prices that are available from the pipeline is shown in Figure 2. The optimization problem of the site can be formulated as follows

max

u_i,r_i,∀i n i=1

∑

p^|_i,prod.y_i−1^(1×m)(P◦R_P)1^(s×1), (1a)

s. t. ∑ⁿi=1r_i−R_P1^(s×1)=0, R_P∈RP, (1b)

Fi(ui,ri):={ui,ri|yi=fi(ui),ri=gi(ui,yi),ui∈Ui},∀i, (1c) where it is assumed that the site strives for a maximization of the sum of the individual objectives (here, product salesp^|_i,prod.yi) under the consideration of the additional costs or benefits that are caused by interfacing the pipelines with the constrained resource amounts given in RP. We denoteA◦Bas the Hadamard product (element-wise multiplication) and1^(s×1)as a column vector withsidentity entries. The matrixP∈R^(m×s)contains the individual prices formresources andsprice regimes in the tariff (cf. Figure 2) andRP∈R^(m×s)is the amount

(3)

pipeline tariff 1 pipeline tariff 2

amount

price

0 10 20 30 40 50 60

Figure 2: Portfolio tariff with different price regimes.

of resources exchanged with the pipelines for each resource at each price. The overall costs or benefits are then computed asP◦Rp. The constraints are on the one hand the network balance Eq. (1b), which should be closed at any time and on the other hand the individual constraint setsFifor each subssystemi=1,2, . . . ,nthat result from technical limitations. In site-wide formulation, the subsystems have a vectorri∈R^(m×1)that indicates the demand or supply, which is independent of the source or sink and where positive numbers indicate demands and negative numbers the supply. If the optimization problem is decomposed by Lagrangian relaxation to set up a price-based coordination algorithm (Bertsekas and Tsitsik- lis, 1997), a single vector of Lagrange multipliers with a single multiplier for each resource is not sufficient, since the site-hub can buy and sell resources at different rates depending on the amount that is taken from or sent to the pipeline. This leads to the following modeling approach.

3. Virtual splitting of the networks on the subsystem level

A standard Lagrangian relaxation of the problem stated in Eq. (1) can be written as the following optimization problem that needs to be solved by each subsystemi

maxu_i,r_i p^|_i,prod.yi−λλλ^|ri, (2a)

s. t. Fi(ui,ri), (2b)

whereλλλis the vector of Lagrange multipliers, which can be interpreted as the vector of prices that are associated with the demand or supply of the shared resources inr_i. To account for different price regimes in the portfolio contract, the constraints of the individual systems have to be extended. To model the different price regimes in a tariff the networks can be split into virtual networks, i. e., each of themresource networks is split intosvirtual networks of the same resource. Here, without the loss of generality, we assume that for each resourcesprice regimes exist. This results in the following formulation (ri,j,l∈R)

r_i=





 ri,1

... ri,m





=







∑^s_l=1ri,1,l

...

∑^s_l=1ri,m,l





=R_i1^(s×1)=







ri,1,1 . . . ri,1,s

... . .. ... ri,m,1 . . . ri,m,s





1^(s×1). (3)

The subsystems’ optimization problems are changed such that for each resource j only one virtual network is allowed to be active. This is realized by a constraint adaptation, announced by the site-coordinator. The reasoning behind this is as follows: If the internal price of a shared resource exceeds the next higher external price (pipeline price in the tariff), the coordinator buys an amount of resource from the pipeline and allocates it to the internal shared resource network. From this point in time on, the subsystems that demanded shared resources receive an allocated amount of resource for the particular network. Afterwards, the amount

(4)

mulation involves the following constraint adaptation, where the resources from the preceding price regimes (t_j−1, withtas a vector storing the active price regimes for each resource j) are frozen and the succeeding virtual networks are set to zero

ri,j,l∈R_i,^(t)_j,l, R_i,^(t)_j,l=







R tj=l 0 l>t_j ˆ

ri,j,l else

, (4)

where ˆr_i,_j,lis the amount of resource that has been bought during the last price regime by the coordinator and that has been assigned relatively to the amount the other subsystems’ demand.

Further, the modeling involves the matrix F^(t), fj,l ∈[0,1], which activates the respective virtual networks. The subsytems’ optimization problems are changed to

max

u_i,R_i,∀i p^|_i,prod.yi−1^(1×m)(ΛΛΛ◦Ri)1^(s×1) (5a)

s. t. Fi(u_i,r_i), r_i−R_iF^(t)1^(s×1)=0 ri,j,l∈R_i,^(t)_j,l, ∀j,l







individual constraints, (5b)

where the manipulated variables of the subsystem are the vector u_i and the entries of the matrixR_i. The vector of Langrange multipliers λλλ is extended to the matrix of pricesΛΛΛ∈ R^(m×s).

4. Proposed coordination scheme

Note, that the proposed update scheme is formulated for buying resources only. The formulation for selling resources to external resources can be formulated analogously . The proposed coordination scheme receives the planned amounts of shared resources from the subsystems as input (see Algorithm 1). After a convergence check, the network balance is evaluated and it is checked whether the Euclidean norm of the balance is below a thresholdε. The coordinator evaluates whether one of the internal prices exceeds the next higher pipeline price that would be available to buy additional quantities of resources. If the coordinator decides to buy additional resources at the pipeline price, the subsystems are queried again for the exact pipeline price before the bought amount is assigned to the subsystems. The assigned quantities are calculated based on the demands of the receiving plants only, i. e., a producing plant is not assigned any resource. If the internal price is lower than the next higher price in the tariff, a normal subgradient update is performed. Whenever the coordinator buys an amount for a specific network, the virtual networks that are linked to the lower-priced tariff regimes are

“frozen”, i. e., the Lagrange multipliers inΛΛΛand the received quantitiesri,j,l are fixed (see constraint in (4)).

5. Case study

The mathematical formulation of the plants’ optimization problems is given in Eq. (5). The manipulated variables of each plant are limited to lie between 0 and 1 (lower and upper bound on the load). The numerical values for the tariff are given in Figure 2. The model equations

(5)

Algorithm 1Price-based coordinator update with constraint adaption.

1: procedureCOORDINATORUPDATE([R₁, . . . ,R_n]) .Input: subsystems’ responses

2: G ←∑ⁿ_i=1R_i−R_P .Subgradient evaluation

3: ifkGk₂<ε then

4: return; .Convergence achieved (Eukledian norm)

5: end if

6: forj=1,2, . . . ,mdo

7: ifΛΛΛj,t_j ≥P_j,t_j then

8: ΛΛΛj,t_j←P_j,t_j .Assign the pipeline price

9: G ←∑ⁿ_i=1R_i(ΛΛΛ)−R_P .Reevaluation of the subsystems

10: r_j,t_j ←min(Gj,tj,r¯_j,l,p) .Buying from the pipeline

11: fori=1,2, . . . ,ndo

12: rˆ_i,_j,t_j ← r_i,j,t_j÷∑ⁿi=1max(r_i,_j,t_j,0)

×r_j,t_j

13: end for

14: t_j←t_j+1

15: F_j,t_j←1

16: else

17: ΛΛΛj,t_j←ΛΛΛj,t_j+SG .Normal Subgradient update

18: end if

19: end for

20: end procedure

for the three plants are:

f1(u1) =

32u²_1,1+8u1,1

24u²_1,2+3u1,2

, g1(u1) =

60u1,1+20 40u1,2+35

, p1,prod.= 5.4

2.1

, (6a)

f₂(u₂) =

35u²_2,1+15u2,1

37u²_2,2+10u2,2

, g₂(u₂) =

50u2,1+10 45u2,2+2

, p_2,prod.= 1.5

2.6

, (6b)

f3(u3) =

25u3,1+15 30u²_3,2+8

, g3(u3) =

−25u3,1−15

−20u3,2+20

, p3,prod.= 1.5

3.2

. (6c)

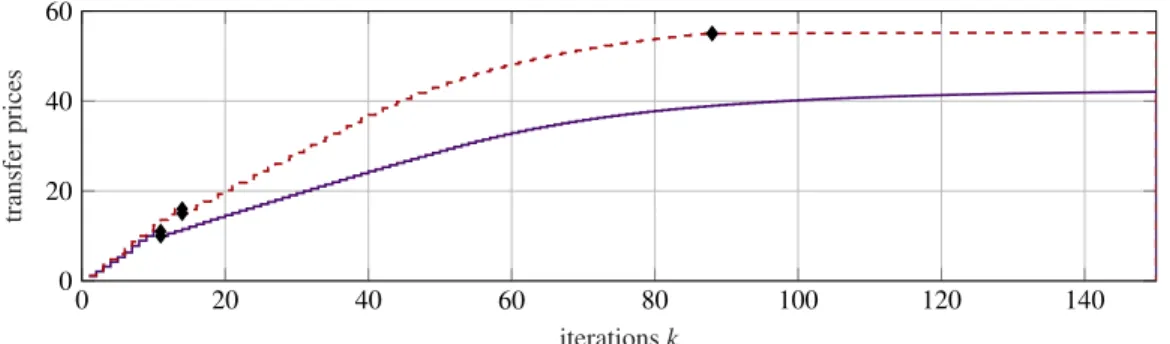
The results of the simulation study using Algorithm 1 withsi,j=i=0.7,si,j6=i=0,si,j∈Sare shown in Figure 3 and Figure 4. It can be seen that when for a particular resource network the price-based coordination leads to a price higher than the next higher pipeline price (diamond symbols in Figure 3), the coordinator buys the available amount from the pipeline for the particular price (see vertical bars in Figure 4). The network balance at these events is reduced until finally the network balance is below the threshold. Upon convergence of the algorithm the final cost a subsystem has to pay is the summation of the costs from each virtual network, i. e., the cost for a particular resource is determined from the amounts that are bought and received externally at different price regimes and the amount that is traded at the equilibrium price on site.

6. Conclusion and outlook

The problem of portfolio tariffs with different price regimes depending on the quantity of shared resource that is retrieved from the pipeline network has been studied and a price-based coordinator update that is aware of the tariff has been proposed. The simulation results show that the coordinator is able to react to the situation by buying certain (limited) amounts of shared resources at fixed rates. The coordination strategy for the investigated case study converges to a solution that is feasible for the two networks and that finds the equilibrium

(6)

0 20 40 60 80 100 120 140 0

20 40

iterationsk

transferprices

Figure 3: Transfer prices against the number of iterations.

0 20 40 60 80 100 120 140

0 10 20

iterationsk

networkimbalance

Figure 4: Network resource balance against the number of iterations.

price by employing a subgradient-based update step. The strenght of the proposed approach is its transparency with respect to the different announced price regimes, i. e., each subsystem has consistent information how its overall cost function is computed. The advantage of price- based coordination is kept and thus the individual cost functions are allowed to remain private.

Future research should be devoted to higher degrees of interactions between the networks, which have usually tight couplings.

Acknowledgment

The project leading to this publication has received funding from the European Union’s Hori- zon 2020 research and innovation programme under grant agreement No 723575 (CoPro, spire2030.eu/copro) in the framework of the SPIRE PPP.

References

D. P. Bertsekas, J. N. Tsitsiklis, 1997. Parallel and Distributed Computation: Numerical Methods. Athena Scientific, Belmont.

S. Boyd, 2010. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers.

Foundations and Trends^R in Machine Learning 3 (1), 1–122.

S. Braithwait, may 2010. Behavior Modification. IEEE Power and Energy Magazine 8 (3), 36–45.

S. Engell, C. Sonntag (Eds.), 2016. Proposal of a European Research and Innovation Agenda on Cyber-physical Systems of Systems, 2016-2025. CPSoS EU Project.

T. Samad, S. Kiliccote, dec 2012. Smart grid technologies and applications for the industrial sector. Computers &

Chemical Engineering 47 (2012), 76–84.

J. Siirola, T. Edgar, dec 2012. Process energy systems: Control, economic, and sustainability objectives. Computers &

Chemical Engineering 47, 134–144.

S. Wenzel, R. Paulen, G. Stojanovski, S. Kr¨amer, B. Beisheim, S. Engell, jan 2016. Optimal resource allocation in industrial complexes by distributed optimization and dynamic pricing. at - Automatisierungstechnik 64 (6), 428–442.