Dynamic Density-Matrix Renormalization for the Symmetric Single Impurity Anderson Model
Volltext
Abbildung
ÄHNLICHE DOKUMENTE
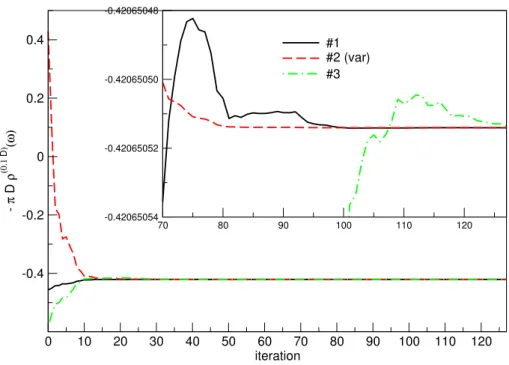
For this, we project out the ground state and use the state | ˜ = (1 − |GG| ) | to study the process of thermalization (in practice, this state | ˜ can be constructed exactly
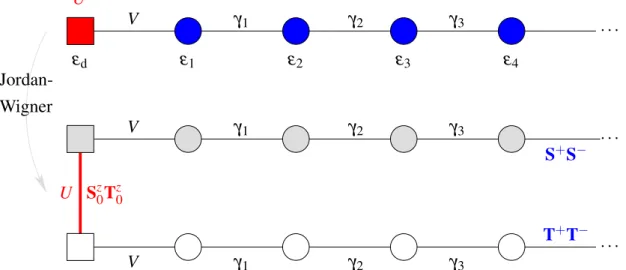
20 The number of hopping operators may depend on the symmetry used: For a chain of spin 1/2 fermions treated in terms of SU(2) × U(1) symmetry, for example, one has a single
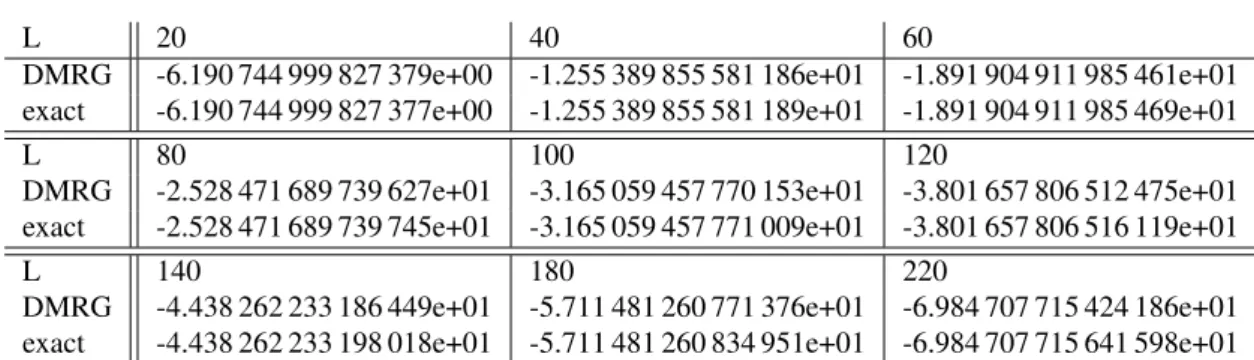
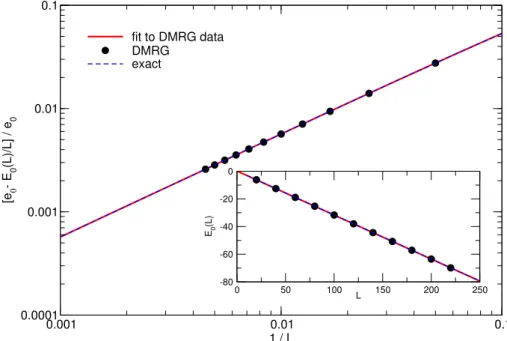
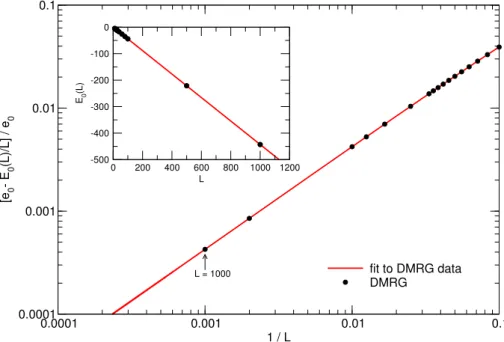
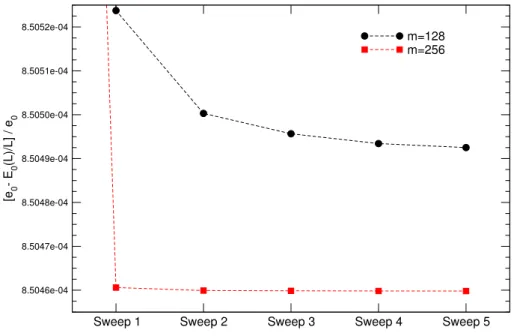
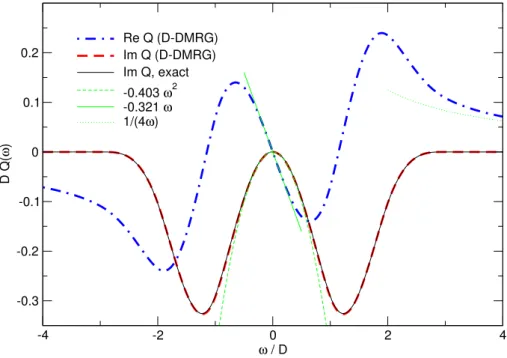
In this paper, we focused on the calculation of the impurity specific heat and the impurity susceptibility of the Anderson model within the FDM approach, 16 finding that this method
Section IV presents numerical results for several interacting quantum dot models of increasing complexity: first the spinless interacting resonant level model (IRLM), then the
This defines the question investigated in this pa- per: Using the flow equation method, we calculate the time-dependent buildup of the electrical current through an Anderson
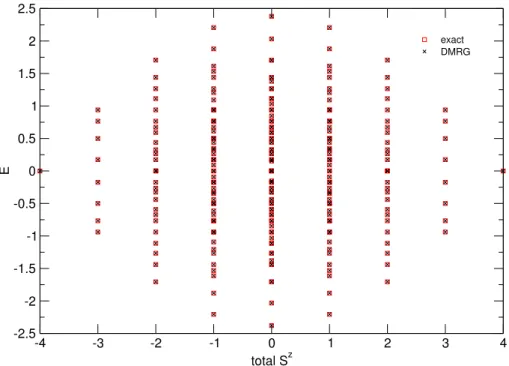
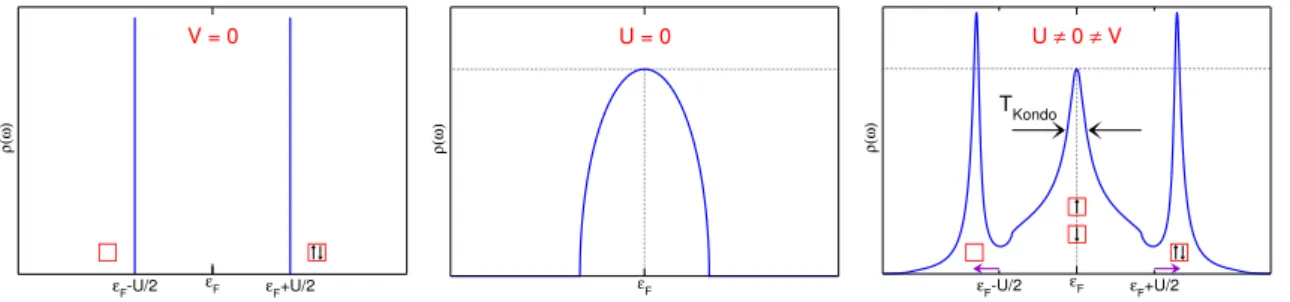
III, the spin-spin correlations constituting the Kondo cloud are investigated and we demonstrate how to extract the value of the Kondo screening length K from the
Second, we also want to create an effective basis that spans a DMRG optimal Hilbert space, i.e., the states we keep for an effective basis are to be the ones having the largest
In the present Chapter, we present the two main theoretical tools for the present work, the multiloop functional renormalization group and the Keldysh formalism, and then a way in