Vorlesungsskript Integrierter Kurs III - spezielle Relativit¨atstheorie

Vorlesungsskript

Integrierter Kurs III - spezielle Relativit¨atstheorie

Marcel Indlekofer, Thomas Lauermann, Vincent Peikert und Raphael Straub 6. Dezember 2004

2

Inhaltsverzeichnis

2 spezielle Relativit¨atstheorie 5

2.1 Einschub: Konzepte & Definitionen . . . . 5

2.1.1 (karthesische) Koordinaten . . . . 5

2.2 Newton’sche Mechanik . . . . 5

2.2.1 Galilei-Invarianz . . . . 5

2.2.2 Widerspruch zur Wellengleichung und zu den Maxwell-Gleichungen mit Galilei-Invarianz . . . . 7

2.3 Relativit¨atsprinzip & Lorentztransformation . . . . 8

2.3.1 Einstein’sches Relativit¨atsprinzip . . . . 8

2.3.2 Konstanz von c . . . . 8

2.3.3 Die spezielle Lorentz-Transformation . . . . 8

2.3.4 Elementare Folgerungen . . . . 10

2.3.4.1 Addition von Geschwindigkeiten . . . . 10

3

4 INHALTSVERZEICHNIS

Kapitel 2

spezielle Relativit¨ atstheorie

2.1 Einschub: Konzepte & Definitionen

2.1.1 (karthesische) Koordinaten

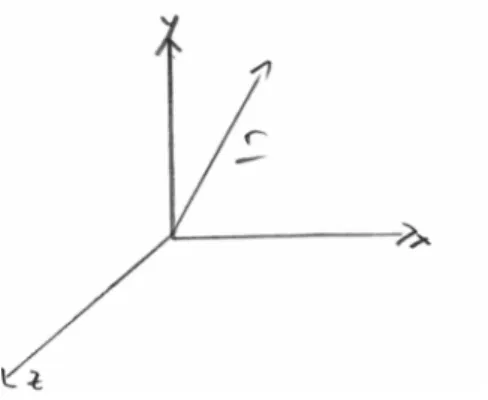
Abbildung 2.1: Raumkoordinaten

Jeder Punkt im Raum besitzt Raumkoordinaten (vgl. Abbildung 2.1):

r=



 x y z



=



 x1

x₂ x₃





Jeder Punkt in Raum und Zeit besitzt Raum-Zeit-Koordinaten:

x=







 ct

x y z







 :=







 x⁰ x¹ x² x³









(2.1)

2.2 Newton’sche Mechanik

2.2.1 Galilei-Invarianz

Newton: ”Mechanische Vorg¨ange laufen in allen Inertialsystemen gleich ab.”

Galilei: ”Zwei Inertialsysteme sind durch eine Galilei-Transformation miteinander ver- kn¨upft.”

5

6 KAPITEL 2. SPEZIELLE RELATIVIT ¨ATSTHEORIE

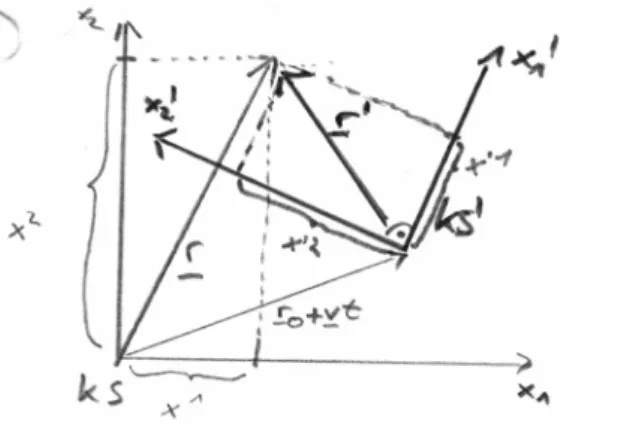
Abbildung 2.2: Galileitransformation

xⁱ =

3

X

j=1

Rⁱ_jx⁰ⁱ+rⁱ₀+vⁱt (2.2)

Rⁱ_j ist eine Drehmatrix.

Bemerkung:Die Indizes f¨ur Koordinatenxⁱ stehen oben und werden mit den Indizes un- ten anRⁱ_j summiert.Abk¨urzung:Im folgenden verwenden wir h¨aufig dieEinstein’sche Summenkonvention:

3,4

X

j=1

Rⁱ_jx^0j =Rⁱ_jx^0j (2.3)

doppelt auftauchende Indizes werden absummiert.

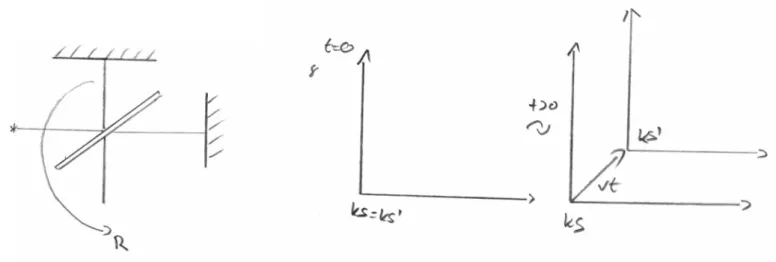
spezielle Galilei-Transformation:

xⁱ =x⁰ⁱ+vⁱt (2.4)

t =t⁰

Die spezielle Galilei-Transformation (Abbildung 2.3) ist eine Transformation auf ein

Abbildung 2.3: spezielle Galilei-Transformation

geradlinig bewegtes Bezugssystem.

2.2. NEWTON’SCHE MECHANIK 7

2.2.2 Widerspruch zur Wellengleichung und zu den Maxwell- Gleichungen mit Galilei-Invarianz

• A) Wellengleichung:

∇²− 1 c²∂_t²

E(r,t) = 0

Die Wellengleichung ist eine Folge der Maxwell-Gleichungen im Vakuum mit der speziellen L¨osung:

E(r⁰,t) =E₀cos(ωt−k·r)

f¨ur ω = ck. Die Galilei-Transformation auf ein mitbewegtes Inertialsystem (mit v =k_k^c) ergibt eine stehende Welle:

E(r⁰,t) =E₀cos(ωt−k·r⁰− k²

k ct) =E₀cos(k·r⁰) welche keine L¨osung der Wellengleichung ist.

Daraus folgern wir, dass sowhol die Wellengleichung als auch die Elektrodynamik nach Maxwell nicht Galilei-invariant sind. Dies ist der Ausgangspunkt der speziellen Relativit¨atstheorie.

• B) Versuch von Michelson-Morley

Man verwende ein Michelson-Intzerferometer und benutzt eine Rotation des Spek-

Abbildung 2.4: Michelson-Interferometer

trometers, um Unterschiede in der Lichtgeschwindigkeit entlang der Wege 1 und 2 zu messen, welche auf Grund der Bewegung der Erde zustande kommen.

Erwarten w¨urde man, dass die Interfernzmaxima N ≈ ^L1+L_λ ^{2 v}_c2

mit der Erdge- schwindigkeit v auf Grund des großen Vorfaktors ^L1+L_λ ² messbar sind. Durch den Vorfaktor sind selbst feinste Unterschiede messbar. Im Versuch wird aber kein Unter- schied beobachtet, somit existiert keine Galilei-Transformation auf das Erdsystem.

Diese Beobachtung ist durch die Konstanz der Lichtgeschwindigkeit cim bewegten Koordinatensystem erkl¨arbar.

8 KAPITEL 2. SPEZIELLE RELATIVIT ¨ATSTHEORIE

2.3 Relativit¨ atsprinzip & Lorentztransformation

2.3.1 Einstein’sches Relativit¨atsprinzip

Die gesamten physikalischen Vorg¨ange laufen in allen Inertialsystemen gleich ab und zwei Inertialsysteme sind durch eine Lorentztransformation verkn¨upft.

2.3.2 Konstanz von c

Die Lichtgeschwindigkeit cim Vakuum ist unabh¨angig vom Inertialsystem und ¨andert sich also nicht bei Lorentz-Transformation.

2.3.3 Die spezielle Lorentz-Transformation

Abbildung 2.5: spezielle Lorentz-Transformation

Die Wellenfront einer Kugel-Lichtwelle, die vom Ursprung in zwei Inertialsysteme ausgeht, muss gleich sein.(vgl. Abb 2.5):

r²−c²t² =r² − x⁰2

=r⁰²−c²t⁰² =r⁰²− x⁰⁰2

(2.5) Zur Vereinfachung w¨ahlt man:

x⁰¹ =x¹ und x⁰² =x²

Licht, die Wellenfront einer elektromagnetischen Kugelwelle, breitet sich aus von einer Welle, die zum Zeitpunktt=t⁰ = 0 am Ortr=r⁰ = 0 war. Das zweite Koordinatensystem KS’ bewege sich mit v =vzˆDie Position der Wellenfront, der sogenannte Lichtkegel l¨asst sich mit folgender Formel beschreiben:

r²−c²t² = (r⁰)²−(ct⁰)² (2.6) Zur Vereinfachung nehmen wir Bewegung in z-Richtung an: x⁰ =x und y⁰ =y

z²−c²t² = (z⁰)²−(ct⁰)² ∗ (2.7) Wenn wir nun die Lichtgeschwindigkeit in allen Bezugssystemen als konstant postulieren, wie lautet dann die zugeh¨orige Koordiantentransformation(KT)? Wir postulieren weiter- hin:

• KT sei linear: λ₁ ct₁

z₁

+λ₂ ct₂

z₂

=λ₁ ct⁰₁

z₁⁰

+λ₂ ct⁰₂

z₂⁰

• KT sei homogen: t=z = 0 wird auf t⁰ =z⁰ = 0 abgebildet.

2.3. RELATIVIT ¨ATSPRINZIP & LORENTZTRANSFORMATION 9 Damit k¨onnen wir KT als Matrix Λ schreiben, die Matrix der Lorenzransformation ge- nannt wird und gegeben ist durch:

x^0µ= Λ^µ_ν ·x^ν (2.8)

als die Transformation von KS nach KS’ mit der Relativgeschwindigkeit v.

ct⁰ z⁰

=

a b f d

· ct

z

(2.9) also ist zum Beispiel Λ⁰₀ = a oder Λ⁰₃ = b. Dann lautet die R¨ucktransformation von KS’

nach KS:

ct z

= 1

ad−bf

d −b

−f a

· ct⁰

z⁰

(2.10) und beschreibt die Transformation mit der umgekehrten Relativgeschwindigkeit v⁰ =−v:

x^µ = Λ^µ_ν(−v)·x^0ν (2.11)

Vergleich von Λ(v) und Λ(−v) und die Isotropieforderung ergibt:

det Λ =ad−bf = 1 sowie a=d (2.12)

Daraus folgt:

det Λ =a²−bf = 1 (2.13)

Sei nun b =vb und f =vf, ergibt sich in Gleichung ∗ eingesetzt:

z²−c²t² = (vf ct+az)²−(act+vbz)² = (a²−v²b²)z² −(a²−v²f²) + 2avc(f −b)zt (2.14) Daraus folgt b =f und somit f¨allt der gemischte Term weg.

⇒ a²−v²b² = 1 (2.15)

Damit k¨onnen wir nun einen Winkel ϕ einf¨uhren, so dass a = d = coshϕ und b = f = sinhϕ mit cosh²ϕ−sinh²ϕ = 1 gilt.

⇒Λ^µ_ν(v) =

coshϕ sinhϕ sinhϕ coshϕ

= coshϕ

1 tanhϕ tanhϕ 1

(2.16) Ein winkel ϕparametrisiert die Lorentztransformation. Mitβ = tanhϕund γ = coshϕ =

√1

1−β² erhalten wir:

Λ^µ_ν(v) = γ·

1 β β 1

(2.17)

10 KAPITEL 2. SPEZIELLE RELATIVIT ¨ATSTHEORIE Abbildung 2.6: Plot der hyperbolischen Winkelfunktionen

wobei |β|<1 gelten muss.

Aus dem Vergleich mit den Galilei-Transformationen f¨ur v → 0 folgt: b → vb(0) und damit ist β(0) = ¹_c. Aus der Hintereinanderschaltung mehrerer Lorentztransformationen kann man zeigen, dass gilt:

β = v

c (2.18)

Damit ist ϕ = artanh^v_c und wir haben die speziellen Lorentztransformationen:

t⁰ = t+^vz_c2

q 1−^v_c2²

(2.19) (2.20) sowie

z⁰ = z+vt q

1− ^v_c²2

(2.21)

welche bei v in die Galilei-Transformationen t⁰ =t und z⁰ =z+vt ¨ubergehen.

2.3.4 Elementare Folgerungen

2.3.4.1 Addition von Geschwindigkeiten

Begr¨undung: β ist linear in v, weil damit Hintereinanderschaltung zweier LT zu den Geschwindigkeiten u und v wieder eine spezielle LT mit der Geschwindigkeit w ergibt.

Hierbei bedienen wir uns einer Gruppeneigenschaft der Lorentztransformationen:

Abbildung 2.7: Wie groß ist w?

Λ^µ_ν(u)·Λ^ν_κ(v) = Λ^µ_κ(w) (2.22)