Fluid Dynamics

(1)

Fluid Dynamics

Prof. Huw C. Davies

WS 2005 / 2006

Version: 1.1

24^th October 2005

(2)

streets” along the direction of wind flow. When the flow is interrupted by an obstacle such as an island, a series of organized eddies can appear within the cloud layer downwind of the obstacle. These turbulence patterns are known as von Karman vortex streets. In this image from the June 6 2001, an impressive vortex pattern continues for over 300 km southward of Jan Mayen island. Jan Mayen is an isolated territory of Norway, lo- cated about 650 km northeast of Iceland in the north Atlantic Ocean. Jan Mayen’s Beerenberg volcano rises about 2.2 km above the ocean surface, providing a significant impediment to wind flow.

Fluid dynamicist Theodore von Karman was the first to derive the conditions under which these turbulence patterns occur. Von Karman was a professor of aeronautics at the California Institute of Technology and one of the principal founders of NASA’s Jet Propulsion Laboratory. (Source:

NASA)

Institute for Atmospheric and Climate Science

(3)

Introduction

παντ α χωρει, σνδεν µενει Heraclitus 5 cent. B. C.

1.1 Natural Flow Phenomena

Flow phenomena in natural fluid systems are pervasive and diverse. Their pervasiveness can be highlighted by noting that the range of fluid media includes: the galactic medium and interstel- lar gas; stellar and planetary atmospheres; planet Earth’s atmosphere-ocean-lake-river system;

our personal cardio-vascular system, pulmonary system, eyes, ears, larynx, alimentary canal, kidneys etc.

The diversity of documented fluid phenomena is linked to the vast range of spatial scales of the forementioned media and to the different physical processes that are active at different spatial scales. As examples of this latter point note that:

• motion in the conducting fluid regions of the Sun is influenced by, and indeed is believed to maintain, the ambient magnetic field

• the vortex like structure of large scale (∼2000 km ) cloud systems in the earth’s atmosphere is related to the earth’s rotation,

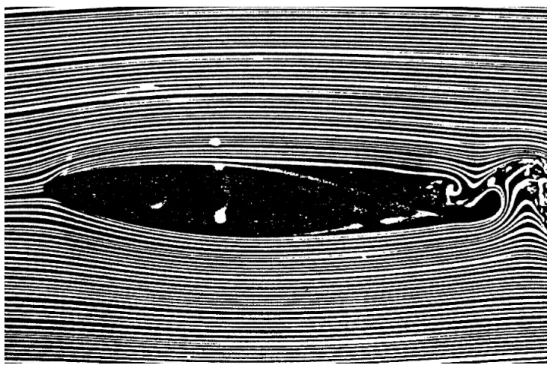
• a rapid change in the surface elevation of a mountain stream (i. e. a so-called hydraulic jump) is usually either associated with the perturbing effect of a submerged obstacle (Fig.

1.1) or is an illustration of the spontaneous transition between two flow states

• secondary circulations and eddies in rivers are often attributable to the geometry of the river bank

A fascinating and profound aspect of fluid dynamics is that there exists an unity within this diversity with different fluid media replicating similar phenomena albeit on a different scale.

Thus for example:

• the essence of the solar magneto-dynamo is believed to be akin to that operating in the earth’s fluid core (Fig. 1.2 (a))

• analogues of atmospheric vortex-like structures are observed in Jupiter’s atmosphere (Fig.

1.2 (b)) and in the earth’s major oceans

(8)

(a) (b)

Figure 1.1: Von Karman vortex street’s from Guadelupe, 20^th August 1999 (a) and idealized Karman street (b).

(a) (b)

Figure 1.2: A great solar helium eruption (a) was taken on December 19, 1973 using the Solar Physics Branch’s Spectroheliograph, complex flow of a dynamic atmosphere around a single spot on the planet Jupiter (b).

(9)

1.2. NATURE OF ENVIRONMENTAL FLUID DYNAMICS 3

• jump-transition phenomena also occur in galaxy-expansions, in the atmospheric Bora, in lake outflows and in the washbasin

• secondary circulations constitute a crucial component of blood flow in the aorta

1.2 Nature of Environmental Fluid Dynamics

Fluid dynamics is the scientific study of the motion of fluids. It is founded upon the basic laws of classical physics as they apply to a fluid continuum. The mathematical formulation of these laws provides the subject with a concise, compact and well established theoretical foundation.

Nevertheless, as noted earlier, it encompasses strikingly disparate topics.

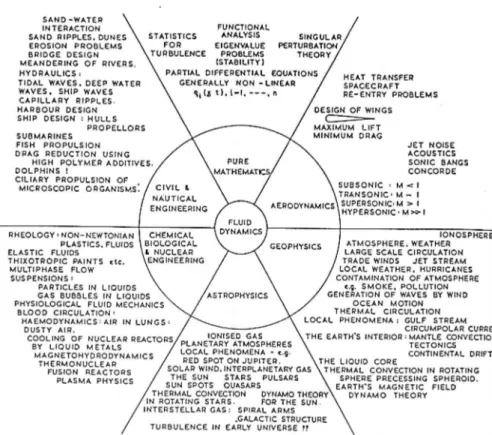
A classification of fluid dynamic studies in terms of sub-disciplines is set out in Fig. 1.3 along with examples of topics in each study-area. A fluid dynamicist would usually be involved with one particular sector of the circle. However the sectors are not independent and growth of understanding or new applications in one sector can, and often does, provide fresh insight or trigger new discoveries in other sectors.

Environmental fluid dynamics is the sub-discipline concerned specifically with the naturally occurring phenomena of the earth’s atmosphere, oceans and enclosed water and ice systems. It embraces topics that in their spatial scale range from the global circulation of the atmosphere and ocean to the flow around and within cloud and spray droplets, and in temporal scale from that associated with air turbulence to that of glacier movement.

From an observational and experimental standpoint environmental fluid dynamics has several distinctive aspects:

• the phenomena of interest occur in natural (and often complex and inaccessible) systems in contrast to controlled laboratory conditions

• the phenomena can often be only partially (and frequently inadequately) observed

• the flow media are essentially our habitat

The general aims of the subject include determinating the structure and seeking an understanding of observed flow patterns, predicting their development and/or controlling or modifying their impact.

(10)

Figure 1.3: The fluid dynamicist’s view of the world.

1.3 Objectives of Course

The underlying aims of the course are:

• To establish the physical framework for examining environmental flow phenomena

• to develop a familiarity with the concepts of fluid dynamics

• to stimulate an awareness of the philosophy (or mode of approach) that characterizes fluid dynamic studies.

The course itself is split into three parts that provide successively:

• a concise, semi-formal (but not over-rigorous) introduction to the physical foundation and the mathematical formulation of the basic laws of fluid dynamics

• a brief overview of some of the general concepts and techniques that are common to most branches of the subject

• a sketch outline of some key ingredients of geophysical fluid dynamics

(11)

Chapter 2

Physical Foundations of Fluid Dynamics

In this sense rational mechanics will be the science of motions resulting from any forces whatso- ever, and of the forces required to produce any motions, accurately proposed and demonstrated.

Is. Newton 1686

In this section we discuss and document the physical foundations ofFluid Dynamics and in so doing highlight the distinctive features of a fluid.

2.1 On the molecular structure of materials

First we consider the distinction between solid, liquids and gases from a micro-physical standpoint. At the corpuscular level this difference can be expressed in terms of the following factors:

• the ratio of the molecular spacing within a material relative to the equilibrium separation length (d0 ∼3−4·10⁻¹⁰ m ),

• the strength of the intra-molecular forces, and

• the extent of the relative movement of molecules.

The strong intra-molecular forces and resultant small relative movement of molecules within a solid are consistent with a sample of solid material possessing a distinct geometric shape and being able to withstand (to a substantial degree) attempts to modify that shape (Table 2.1). In contrast the properties of liquid and gases indicate that a fluid sample would neither exhibit a preferred spatial configuration nor be able to withstand (to any degree) an attempt to distort its Table 2.1: The relationship between molecular - spacing, -forces and -movement within a solid, liquid and gas.

Molecular Intra-molecular Molecular Movement

Spacing Forces Individual Relative

solid very small strong small vibrations severely constrained

liquid ∼1 medium curved intermediate

gas very large weak piecewise linear rel. unconstrained

(12)

shape. Again the continuous movement of molecules within a fluid is associated with a perpetual transfer of momentum and heat within the fluid.

It is the mode of description and manifestation of these features on the macro-scale that we consider in the subsequent sub-sections.

2.2 The Continuum Hypothesis

Environmental fluid dynamics is usually concerned with flow phenomena that occur on the macroscopic scale, i. e. on spatial scales that are large compared with the distance between the individual molecules and on temporal scales much greater than the average time between the successive ‘molecular encounters’ of a particular molecule. On the macroscopic scale it has been proven to be appropriate to regard a fluid as a continuum i. e. to invoke a Continuum Hypothesis for the fluid medium.

In this framework physical quantities such as the mass and momentum associated with matter contained within a given ’small’ volume are assumed to be spread uniformly within that volume. The values assigned to these macroscopic quantities can be viewed as ’phase-averages’

of the mass and momentum associated with the molecules that, in reality, occupy only a small portion of that same volume. In essence the Continuum Hypothesis implies that the medium is indefinitely divisible without losing any of its defining properties and hence connotes a description of a flow system as a continuous field. Thus in the context of this Hypothesis expressions such as a point in the fluid, the density momentum and temperature at a point in the fluid, and a fluid particle are rendered meaningfull. In effect the expression the displacement of a fluid particle is not related to the displacement of some particular molecule. To avoid con- fusion and to highlight the underlying distinction between the micro- and macro-scopic frames we shall use the term fluid parcel and not fluid particle for the presumed fundamental fluid entity.

The Continuum Hypothesis provides the framework for studing fluid motion as one of the Field Theories of Classical Physics. It is important to be aware that an Hypothesis has been made, but also to recognize that one need not look far for an apologia:

• an integral aspect of the scientific approach is that of formulating a hypothesis

• in the present context a programme based upon the continuum hypothesis is eminently workable, whereas an approach based upon the laws governing elementary particles is invariably demonstrably impractical.

The programme is in effect to apply the laws of Classical Physics to a fluid medium. These laws include the principle of mass conservation, Newton’s law of motion, an equation of state and the first and second laws of Thermodynamics.

2.3 Forces acting on a fluid

In the context of the continuum hypothesis there are two kinds of forces that can act on a fluid parcel namely,

• body forces acting on the entire fluid parcel, and

(13)

2.3. FORCES ACTING ON A FLUID 7

• surface forces acting exclusively on the surface of the parcel.

We consider these two categories in turn.

1. Body Forces

These are forces that can ’act at a distance’, or in effect penetrate a fluid. Examples are the gravitational, magnetic and electrical fields. They act uniformly on the entire fluid parcel and the total force is proportional to the volume of the parcel.

i. e. Total Force = F(r, t)ρ dV,

F= the force per unit mass (it can be a function of both space and time) dV = volume of fluid parcel

In an environmental context the body force of principle interest is the gravitational field.

Newton’s law of universal gravitation states that two bodies of mass M and m whose centers of mass are separated by a distance r, experience a force of attraction such that,

F=−G M m r²

r

r (2.1)

Here F is the force exerted on the body of mass m due to the gravitational pull of the body of massM, and Gis the so-called gravitational constant.

The body force per unit mass on a fluid parcel in the atmosphere or ocean due to the gravitational attraction of the earth is given by

F

m ≡g^∗ =−G M r²

r

r (2.2)

whereM is now the mass of the earth andris essentially the radial location of the parcel.

Rewriting r in the form

r =a+z (2.3)

whereais the mean radius of the earth (If the earth’s sphericity is neglected thenz is the departure height from sea-level). It follows that

g^∗ =− g

1 +^z_a² k. (2.4)

Moreover since (z/a)1 for most environmental flow systems,

g^∗ ≈ −gk. (2.5)

Here g= (G M/a²)≈9.81 m s ⁻² andk is in the direction of the local vertical.

2. Surface Forces

These forces can be viewed as the interaction of parcels that are juxtaposed (i. e. in ’me- chanical contact’), and expressed as the stress (i. e. force per unit area) acting on the surface of the parcel. This stress has components both normal and tangential to the surface. To define the stress, let τ_xy represent the stress components in the x-direction acting at the point 0 on the surface of a fluid parcel whose local outward normal is is in the positive

(14)

y-direction.

It then follows that the stress is specified by τ_ij, the components of the stress matrix,

τ_ij =





τ_xx τ_xy τ_xz τ_yx τ_yy τ_yz τzx τzy τzz



 (2.6)

The surface forces in a fluid are molecular in origin and owe their existence in part to the momentum transfer accomplished by the movement and ’collision’ of molecules. We consider in turn two components of the surface stress - the pressure stress and the viscous stress.

(a) Pressure stress

A fluid exerts a normal stress even when it is stationary on the macro-scale. Consider for example a fluid confined in a container and at rest. It will nevertheless exert a

’thrust’ on the side-walls of the container due to the continual molecular bombardment of the walls. In this case the thrust will be normal to the wall since the net effect of the along wall velocity components will cancel. This normal thrust expressed as a force per unit area is the pressure (p) exerted by the fluid on the container wall. It follows that at the boundary the fluid itself experiences a stress of (−p). What is the counterpart of this thrust at a location immersed within the fluid? In effect a purely geometric plane surface within the fluid experiences an equal and opposite thrust on its two sides. More generally an arbitrary fluid parcel experiences this thrust acting normally at every point on its surface. (A proof for the non-dependence of pressure upon direction is given in Appendix I.) It follows in terms of the stress matrix τ_ij, that for a fluid at rest,

τ_xx=τ_yy =τ_zz =−p(x, y, z, t). (2.7) A more vivid illustration in Fig. 2.1 is to consider a liquid of uniform densityρat rest in a gravitational field−gk. A horizontally aligned layer of width ∆zwould experience a downward force per unit length ofgρ(∆z). The fluid is at rest and thus in the absence of other forces the gravitational effect can only be offset by the difference in the pressure on the upper and lower surfaces of the stipulated layer i. e. a balance of the normal force components implies that

(p+ ∆p) +g ρ(∆z) = p , (2.8)

i. e. ∆p

∆z = −g ρ ,

and in the limit of an infinitely thin layer (i. e. ∆z → 0) we obtain the so-called hydrostatic relationship

(15)

2.3. FORCES ACTING ON A FLUID 9

z

x y

∆z

p + ∆p

p

Figure 2.1: Schematic concept of the hydrostatic relationship.

∂p

∂z =−g ρ (2.9)

Hydrostatic relationship In this particular case we have merely considered the effect of vertical variations of the pressure field upon a fluid parcel, and shown it takes the form (−∂p/∂z). In general the ’effective-stress’ associated with the pressure field is of the form

−(∇p) =− ∂p

∂xi+ ∂p

∂yj+∂p

∂zk

(2.10) (b) Viscous Stress

We have already noted that the continuous movement and ’collision’ of molecules within a fluid is associated with perpetual transfer of momentum and heat within a fluid. In a fluid at rest there is no net macro-scale effect. However if the fluid is in differential motion (i. e.v6= constant) or has a non-uniform temperature distribution (T 6= constant) then a net flux of momentum or heat can ensue.

To illustrate this consider the idealized experimental set-up of water confined between two parallel plates (see Fig. 2.2) with the upper plate in uniform motion (u = U₀) and the lower plate held fixed. It is found that (at least for U₀ small) a constant tangential stress (−τ_xz) has to be applied to keep the plate moving at this velocity and the velocity profile, u = u(z), of the flow is steady and increases linearly from zero at the base to u=U₀ at the top. It follows that

• the fluid establishes a force resisting the motion of the plate, and

• the stress is sustained across the entire fluid depth, so that a horizontal surface (z = z₀) within the fluid experiences equal and opposite tangential stresses on its two sides. In effect the faster fluid atz=z₀₊ tends to draw the lower slower layer along with it, whilst the lower layer acts to retard the upper layer.

The realized stress on a fluid parcel is the so-called ’viscous stress’. For a gas the stress is established almost entirely by the differential transport of momentum by

(16)

u = 0 u = U0 z

d

Figure 2.2: Idealized experiment of a moving plate between water.

upward and downward moving molecules that carry with them a value of x-directed momentum characteristic of their layer of origin. For a liquid both this process and the modification of the intra-molecular forces by the differential motion are important.

It is appropriate to sub-divide the surface stress matrix into two components to take cognizance of the two generating mechanisms of pressure and viscous effects

i. e. let τ_ij= −p δ_ij

| {z } pressure

+ τ_ij⁰ deviatoric stress|{z}

(2.11)

where δij = 1 if i=j δ_ij = 0 if i6=j and τ_xx⁰ =tau⁰_yy =τ_zz⁰ = 0 .

Note that the (−p) is consistent with an inward directed pressure force on a fluid parcel.

The two foregoing surface forces, are related respectively to the intrinsic thermodynamic and flow properties of fluids and are considered further in the next two sub-sections.

2.4 Constitutive Relationships

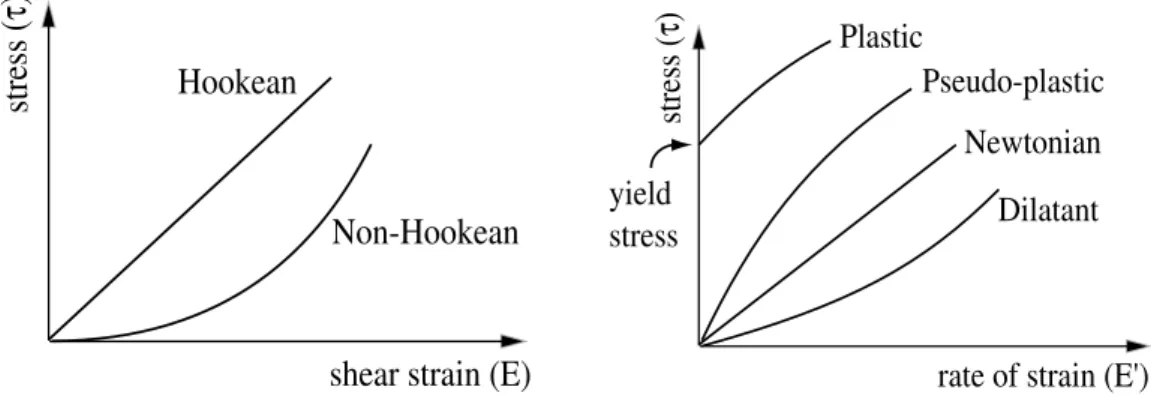
Here we discuss the distinction between solids and fluids from the macrophysical/continuum standpoint. Consider the experimental set-up of Fig. 2.3 with an arbitrary material placed between the two plates, the upper plate generating a constant stressτ_xz =τ, and the lower plate again held fixed. The response of the material can be assessed in terms of the shear strain E = δ/d (the angle of distortion) or to the rate of strain E⁰ (the rate of change of the angle of distortion). An alternative, at least for materials that deform continuously, is to maintain a constant strain rate (ε⁰) and measure the stress (τ).

The strain response to an imposed stress (or the converse) is a property of a material’s constitution. The resulting relationship, e. g.

τ =τ(E, E⁰) or E⁰=f(τ, t) (2.12)

defines the Constitutive Equation or the Rheological equation of state. (Rheology - the science of deformation and flow of matter).

(17)

2.4. CONSTITUTIVE RELATIONSHIPS 11

τ z

d

δ

Figure 2.3: Idealized experiment of a moving plate between water.

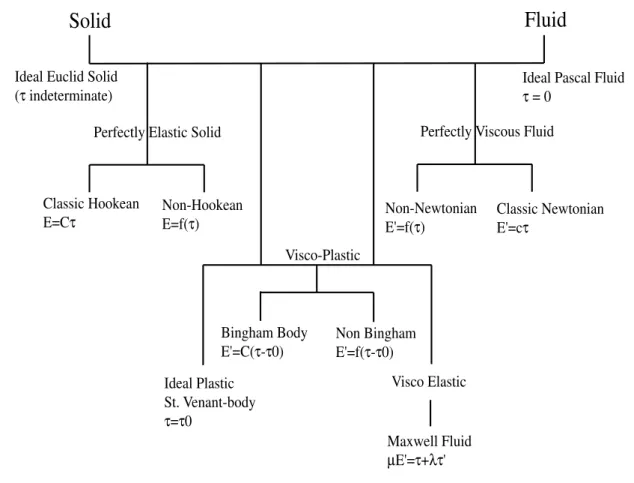
A classification of various conceivable forms of continuous media and their constitutive equations are shown in Fig. 2.5. An idealized ’Euclid Solid’ would be undistortable irrespective of magnitude of τ, whilst for a perfectly ’Elastic Solid’ the shear strain would be purely a function of τ (cf. Hooke’s Law for a spring states that the force is proportional to the extension). In this latter case the material would respond to a shear stress by distorting to a modified equilibrium configuration and would recover its original shape on cessation of the external stress.

At the other extreme an ideal ’Pascal Fluid’ would deform continuously (i. e.E⁰ 6= 0) without an associated shear stress (so that τ /E⁰ = 0) whilst for a perfectly ’Viscous Fluid’ it is the rate of shear strain (E⁰) that would be purely a function of τ (cf. Newton’s statement in 1686 that

’the resistance arising from want of lubricity in the parts of the fluid is, other things being equal, proportional to the velocity with which the parts of the fluid are separated from one another’).

Other hybrid materials are also categorised in Fig. 2.5. For example visco-plastic substances that require the stress to exceed some threshold value before exhibiting fluid properties, and visco-elastic substances for whichE⁰ =E⁰(τ, τ⁰) so that the fluid has some ’memory’ features.

stress (τ)

shear strain (E) Hookean

Non-Hookean

stress (τ)

rate of strain (E') Newtonian

Dilatant Pseudo-plastic Plastic

yield stress

Figure 2.4: Illustration of the (E,τ) and (E’,τ) profiles of the various categories.

In this course we shall concentrate almost exclusively on Newtonian Fluids. This restriction is appropriate since air and water are, to a very good approximation, Newtonian in behavior, i. e.E⁰=c τ, or equivalent τ =µ E⁰.

The second form of the constitutive relationship (τ = µ E⁰) emphasizes the fact, that al- though a fluid can not withstand (to any measure) a force that acts to distort its shape it

(18)

Perfectly Elastic Solid Ideal Euclid Solid

(τ indeterminate) Ideal Pascal Fluid

τ = 0

Fluid Solid

Perfectly Viscous Fluid

Non-Newtonian E'=f(τ)

Visco-Plastic Non-Hookean

E=f(τ) Classic Hookean

E=Cτ

Visco Elastic Non Bingham E'=f(τ-τ0) Bingham Body

E'=C(τ-τ0)

Classic Newtonian E'=cτ

Maxwell Fluid µE'=τ+λτ' Ideal Plastic

St. Venant-body τ=τ0

Figure 2.5: Types of continuous media.

Table 2.2: Classification of some natural media are listed below.

Material Constitutive Relationship(s) Newtonian: air, water E⁰=cτ ⇒τ =µE⁰

Non-Newtonian: milk (Pseudo-Plastic) blood

glacier-ice E⁰=Aτ³ ⇒τ α(E⁰)¹³ orE⁰ =aτ³+bτ orτ =arcsinh(E⁰)¹³ Visco-Plastic: oceanic pack-ice E⁰=Btanh⁻¹(τ /π+ 1) (non-Bingham)

nevertheless establishes an internal stress that resists the resulting motion. The ratio µ=τ /E⁰ for a steady flow is referred to as the coefficient of viscosity of a fluid. In qualitative terms viscosity represents the property of a fluid to establish an increasing resistance to deformation for an increasing rate of deformation The molecular transport and the inter-molecular forces that contribute to viscous stress are different for different fluids and are also temperature dependent.

Thus the coefficient of viscosity (µ) varies from fluid to fluid and has a temperature dependence.

(19)

2.5. EQUATION OF STATE 13

Table 2.3: Viscosity of some common fluids.

fluid µ[ kg m⁻¹s ⁻¹] ν[ m ²s⁻¹] air (0^◦C) 1.70· 10⁻⁵ 1.32 · 10⁻⁵ air (20^◦C) 1.80· 10⁻⁵ 1.50 · 10⁻⁵ water (0^◦C) 1.80· 10⁻³ 1.80 · 10⁻⁶ water (20^◦C) 1.00· 10⁻³ 1.00 · 10⁻⁶ blood (37^◦C) 4.00· 10⁻³

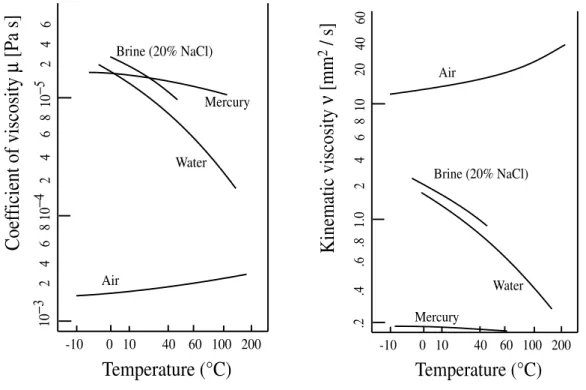
The fluid parcel acceleration to be associated with a given viscous stress would be proportional to µ/ρ (since acceleration α force/density). Thus the value of the so-called kinematic viscosity ν = µ/ρ is also of interest. The values of µ and ν for air and water, displayed as a function of temperature, are given in Fig. 2.3.

Note the typical values of µand ν for air and water at ordinary temperatures and pressure (Table 2.3 and Fig. 2.6).

Thus µ_air/µ_water ≈ 1/60, whereas ν_air/ν_water ≈ 14 (i. e. when ν is the relevant quantity water is in effect a much less viscous fluid than air).

-10 0 10 40 60 100 200

Temperature (°C)

10−3 2 4 6 8 10−4 2 4 6 8 10−5 2 4 6Coefficient of viscosity µ [Pa s]

Air

Water Brine (20% NaCl)

Mercury

-10 0 10 40 60 100 200

Temperature (°C)

.2 .4 .6 .8 1.0 2 4 6 8 10 20 40 60Kinematic viscosityν [mm2 / s]

Air

Water Brine (20% NaCl)

Mercury

Figure 2.6: Coefficient of viscosity (left) and kinematic viscosity (right) of common fluids.

2.5 Equation of state

The concept of the ’thermodynamic state of a fluid’ is based upon a comparison of different samples of a fluid that are in equilibrium. Two samples would be in the same ’state’ if their properties did not change upon being brought into direct contact with one another. It is usual to characterize the state of a fluid by its chemical composition, temperature and pressure. Two

(20)

samples that differed in their chemical composition and temperature would have their properties (i. e. the value of these variables) modified by diffusive processes, whilst a pressure difference would constitute an inter-sample force which would be inconsistent with the maintenance of an equilibrium state of rest. Other ’secondary’ properties of state are then defined in terms of these state variables, and in particular the equation for density is normally referred to as the Equation of State.

The atmosphere and natural water bodies are composed of a mixture of substances. Here we shall consider the Equation of State for sea water and air.

1. Sea water

contains dissolved salts (principally chloride and sodium), plankton, organic debris, dust and, near the surface, bubbles. Below the surface zone only the salts are significant and moreover their relative ratios are almost constant. In this case the chemical composition can be specified in terms of a single variable. Thus below the surface zone the equation of state for sea water takes the form

ρ=ρ(s, T, p) (2.13)

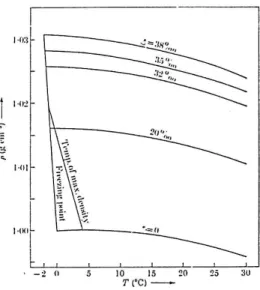
The salinity, s, is the ratio of the weight of dissolved salts to the weight of the sample of sea water (≈ 33-37 parts per thousand). An indication of the value of ρ for water of different salinities is displayed in Fig. 2.7 as a function of temperature. (Note that pure water has a maximum density at T ≈ 4^◦C - the temperature of the deeper layers of all major freshwater lakes in thermally cold atmospheric environments.)

Figure 2.7: The density of water with different salinities as a function of the temperature.

Detailed tables of the dependency of ρ upon s, T, and p have been compiled and are available. Some estimate of the relative importance of variations in s, T, and p can be obtained as follows:

Consider the variations of δρ such that ∂ρ

ρ

≈ 1

ρ

∂ρ

∂T

p,s

dT + 1

ρ

∂ρ

∂p

s,T

dp+ 1

ρ

∂ρ

∂s

p,T

ds

(21)

2.5. EQUATION OF STATE 15

≈ −α dT + 1

K dp+β ds (2.14)

where α, β and K denote respectively the coefficients of thermal and salinity expansions and the bulk modulus. For the normal range of values of p, T and s(excluding the deep ocean), α ≈ 10⁻⁴K⁻¹, K ≈ 10⁹N m⁻², β ≈ 1. It is evident on assigning the typical values to dT, dpand dS respectively of ≈(10 K , <10⁵N m ⁻², 10⁻³), that the pressure induced variations are not significant.

For many fresh-water applications it is appropriate to approximate the equation of state to the form

ρ=ρ_∗1−α^∗θ_∗² (2.15)

where θ_∗ = (T −T^∗), ρ_∗ = ρ_∗(T^∗) and to assign values for T^∗ (the temperature of maximum density) and α^∗, that are based upon the characteristic value of the salinity of the water body e. g. for pure water T^∗ = 4^◦C, α^∗ ≈ 6.8·10⁻⁶K ⁻². Again for fresh water systems with comparatively small temperature variations the equation of state can be approximated by a linear relation of the form

ρ=ρ_∗ 1−α⁰θ_∗ (2.16)

2. Air

The relative proportions of the main constituents of the atmosphere are, with the exception of water vapor, comparatively constant. Thus again the composition of air is satisfactorily prescribed by specifying one variable. In this case an appropriate variable is the specific humidity (q) which describes the mass of water vapor per unit mass of air. The equation of state for air is given to a good approximation by that for an ideal gas. Thus for example for dry air

p_d V = m_d R T , (2.17)

i. e. p_d = ρ_d R T ,

where ρ_d =m_d/V andR =R^∗/M = 287 J kg ⁻¹K⁻¹. Here the subscriptd refers to dry air,R^∗ denotes the universal gas constant, and M the molecular weight.

Similarly for water vapor,

e=ρ_v R_v T (2.18)

where e is the water vapor pressure, ρ_v the mass of water vapor per unit volume and Rv =R^∗/Mv.

It follows, from the partial pressure equation, that the pressurepfor moist air is given by

p = p_d+e (2.19)

Note also that ρ = ρ_d+ρv ,

so that ρ_d = (1−q)ρ since q = ρ_v ρ It follows that:

e

p = q

ε+ (1−ε)q , where ε= M_w M_a = R

R_v (2.20)

(22)

This is an equation that expresses the vapor pressureeof the atmosphere in terms of the specific humidityq.

Furthermore the gas equation can be rewritten in the form

ρ = p

R T_v , (2.21)

where Tv = T

1−q+q ε

is the virtual temperature.

Note that we can write T_v in the form

T_v =T (1 + 0.6078q) (2.22)

Virtual temperature

and sinceq∼O(10⁻³) it follows that for most of the atmosphere, excluding the extremely moist regions of the tropics, the approximation T_v ≈ T is appropriate. This in turn indicates that the equation of state for the atmosphere can be reasonably represented as that for an ideal gas

i. e. p=ρ R T or p α=R T with α= 1

ρ (specific volume) (2.23)

Ideal gas law

(23)

Chapter 3

Mathematical Formulation of the Basic Laws

Mathematicas disciplinas, non leviter, tametsi perfunctorie attingendus esse putamus.

Huldrich Zwingli

3.1 Description of Flow

3.1.1 Coordinate Specification

The continuum hypothesis enables us to readily describe the structure of a flow field (e. g. the instantaneous velocity or density distribution). Two distinct methods are available for assigning values for these continuum variables Eulerian and Lagrangian Coordinates.

1. Eulerian Specification

This is aspace specific coordinate frame. Flow quantities such as the velocityvor density ρ are defined as functions of time t and position in space r = (x, y, z), i. e.v = v(r, t) and ρ = ρ(r, t). Thus for example the motion of the fluid in a given time interval [t] is specified completely if the velocity v is known as function of the independent variables r and tfor all locations in the fluid medium during that time interval. In effect this specification provides a portrayal in 3D-space of the spatial flow structure at each instant in time.

2. Lagrangian Specification

This is aparcel-specific coordinate frame. Flow quantities are defined as functions of time tand parcel location in spaceA= (a, b, c), i. e.v=v(A, t) andρ=ρ(A, t). Now the flow field is specified in terms of the location of each fluid parcel in time and space - a parcel at A0 = (x0, y0, z0) at time t =t0 is at A at time t, and the parcel velocity is given by v = A⁰ = dA/dt. In this reference frame the specification provides the time history of each fluid parcel.

The Lagrangian specification (which was actually proposed by Euler) is in a sense the more fundamental and has proved most insightful in certain special situations. In general however the Lagrangian specification is a cumbersome observational frame for flow exper- iments and an intractable mathematical base.

(24)

Here we shall adopt the Eulerian framework. However we will make extensive use of one essentially Lagrangian concept. This is the concept of the time rate of change of physical quantities associated with a fluid parcel, or the so-called material derivative.

3.1.2 The Material Derivative

The mathematical formulation of this Lagrangian concept in an Eulerian framework can be derived as follows:

Letψbe a physical quantity associated with a fluid parcel. The rate of change ofψin a fluid parcel (i. e. the advected rate of change, or the material derivative) will be denoted byDψ/Dt.

Consider a fluid element atr= (x, y, z) at a time tand moving with a velocity v= (u, v, w).

At a later time T = (t+δt) the particle will arrive at r = (r+δr) = (X, Y, Z), where δr = (δx, δy, δz) = (u δx, v δy, w δz).

Then Dψ

Dt = lim

δt→0

ψ(X, Y, Z, T)−ψ(x, y, z, t) δt

. (3.1)

We writeψ(X, Y, Z, T) as a Taylor series expansion aboutψ(x, y, z, t) so that

ψ(X, Y, Z, T) =ψ(x, y, z, t) + ∂ψ

∂t

u δt+ ∂ψ

∂x

u δt+ ∂ψ

∂y

v δt+ ∂ψ

∂z

w δt+· · · (3.2) It follows that

Dψ Dt = ∂ψ

∂t +u∂ψ

∂x +v∂ψ

∂y +w∂ψ

∂z (3.3a)

Material derivative or equivalently

Dψ Dt = ∂ψ

∂t + (v· ∇)ψ (3.3b)

In particular note that the acceleration of a fluid parcel takes the form Dv

Dt = ∂v

∂t + (v· ∇)v (3.4)

= ∂v

∂t −(v ∧ (∇ ∧ v)) + 1

2∇(v²). (3.5)

The equivalence of the relationships in equations 3.3a / 3.3b serves to underline the mathematical distinction between the material derivative (D/Dt) and the local time derivative (∂/∂t).

An illustration of this distinction from a physical standpoint is shown in Fig. 3.1. Here ψcon- notes the flow pattern perceived by an observer who is either stationary (panel a) or moving with the same velocity as the wave (panel b).

(25)

3.1. DESCRIPTION OF FLOW 19

Figure 3.1: Shear layer flow with traveling instability waves: (a) streamlines seen by stationary observer. (b) streamlines seen by observer traveling at the wave velocity, and (c) filament lines.

(from Hama, 1962)

3.1.3 Some Terminology Related to Flow Description

In the context of flow specification it is useful to refer to various standard ’observationally- related’ modes of flow description:

1. A parcel path (or trajectory) is the curve traced out by a fluid parcel as it moves within a fluid i. e. the path represents the Lagrangian time history of an individual parcel. It can be visualized as follows: Consider a fluid medium in which one parcel is illuminated then a long-time exposure picture would reveal the parcel path.

2. A streak line (or filament line) demarks the location of all fluid parcels that at an earlier instant in time passed through a certain point in space. It can be visualized by picturing the display formed by continually injecting a ’neutral’ dye into the flow at the chosen location.

3. A streamline is a curve that at a given instant is everywhere tangential to the velocity vector i. e. the flow is along the streamline at the instant connsidered. It follows that the family of streamlines at a given time is defined by

dx u = dy

v = dz

w (3.6)

Streamlines

Fluid Dynamics

Fluid Dynamics

Contents

Chapter 1

Introduction

Chapter 2

Physical Foundations of Fluid Dynamics

Chapter 3

Mathematical Formulation of the Basic Laws