Scheinregressionen, kointegrierte Prozesse und FehlerkorrekturmodelleEine Strategie zur Modellierung langfristiger Gleichgewichtsbeziehungen und kurzfristiger Effekte*

(1)

20 2 © F. Enke Verlag Stuttgart Zeitschrift für Soziologie, Jg. 26, Heft 3, Juni 1997, S. 202-221

Scheinregressionen, kointegrierte Prozesse und Fehlerkorrekturmodelle

Eine Strategie zur Modellierung langfristiger

Gleichgewichtsbeziehungen und kurzfristiger Effekte*

Helmut Thome

Institut für Soziologie, Martin-Luther-Universität Halle-Wittenberg, D-06099 Halle (Saale)

Z u s a m m e n fa s s u n g : Zeitreihendaten eröffnen im Prinzip die Möglichkeit, sowohl kurzfristige Effekte als auch lang

fristige strukturelle Beziehungen zwischen Variablen simultan zu schätzen. Dabei wird die in der Querschnittanalyse meist nur implizit gemachte Voraussetzung aufgegeben, die Daten befänden sich zum Zeitpunkt der Messung im Gleichgewicht. Um die sich daraus ergebenden Vorteile dynamischer Analyse nicht zu verspielen, müssen die in Zeitrei

hen typischerweise vorhandenen stochastischen oder deterministischen Trendkomponenten korrekt identifiziert und modelliert werden. Anderenfalls erliegt man leicht der doppelten Gefahr der Scheinkausalität einerseits, der scheinba

ren Nicht-Kausalität andererseits. D ie hier vorgestellten Kointegrations- und Fehlerkorrekturmodelle sind - unter be

stimmten Voraussetzungen - geeignet, dieses Dilemma zu vermeiden. Sie sind aber bisher in der Soziologie kaum rezi

piert worden, obwohl ihnen in den Sozialwissenschaften ein erhebliches Anwendungspotential zukommen dürfte. Zur Veranschaulichung werden strukturelle Zusammenhänge zwischen der „Popularität“ der SPD, den aggregierten Ein

schätzungen zur allgemeinen wirtschaftlichen Lage und dem Niveau der Arbeitslosigkeit in der Periode von Februar 1971 bis Sept. 1982 untersucht.

L Einführung

Zeitreihenanalysen haben in der Soziologie, an

ders als in der Politikwissenschaft,1 noch nicht recht Fuß gefaßt. Sofern überhaupt Zeitreihenda

ten soziologisch analysiert werden, z. B. über län

gere Zeiträume erhobene Kriminalitätsraten, wird das Potential dynamischer Analysemodelle mei

stens nicht ausgeschöpft* 1 2 oder es wird mit statisti

schen Modellen gearbeitet, die für die gegebene Datenstruktur nicht angemessen sind. Soziolo

gisch relevante Zeitreihen, die mindestens 50 mög

lichst gleichabständige Meßzeitpunkte umfassen, sind noch Mangelware. Soweit sie vorliegen, sind sie in der Regel in Form von Aggregatdaten (für Populationen oder Teil-Populationen) gegeben und ziehen somit die üblichen - häufig falschen - Argumente auf sich, die allgemein gegen Aggre

gatdatenanalysen vorgebracht werden.3 Die Da

tenlage verbessert sich jedoch fortlaufend; Hypo

Ich danke Steffen Kühnei, Rainer Metz und Thomas Rahlf für ihre wertvollen Hinweise und Kommentare zu früheren Manuskriptfassungen

1 Das gilt insbesondere für die Politikwissenschaft in den U S A - siehe die jüngeren Jahrgänge in American Political Science Review, die verschiedenen Beiträge des Jahrbuchs Political Analysis (oder der Vorgänger-Zeitschrift Politi

cal Methodology) oder Editionen wie die von H. Norpoth et al. (1991).

2 Siehe aber Eisner (1987; 1992).

3 Eine schlagende Entkräftung einiger dieser Argumente liefert Erbring (1990).

thesen und Fragen, die sich auf Trends, Struktur

brüche und lang- oder kurzfristige strukturelle Zu

sammenhänge beziehen, sind im Übermaß vor

handen. Es könnte also durchaus nützlich sein, sich mit zeitreihenanalytischen Methoden auch in der Soziologie ernsthaft zu befassen.

Strukturmodelle, wie sie üblicherweise in den im

mer noch dominierenden Querschnittanalysen an

gewandt werden, beinhalten etliche Annahmen, die generell problematisch sind und in der Zeitrei

henanalyse aufgegeben oder variabel gehandhabt werden können. Dazu gehört vor allem die Vor

aussetzung, die Daten befänden sich zum Zeit

punkt der (einmaligen) Messung im Gleichge

wichtszustand.4 Andererseits verletzen Zeitreihen

daten in der Regel Annahmen, die in der Quer

schnittanalyse normalerweise als unproblematisch angesehen werden. Die zeitlich geordneten Mes

sungen am gleichen Objekt sind in der Regel nicht Realisationen unabhängiger „Zufallsexperi

mente“, sondern korrelieren miteinander. Diese

„Autokorrelationen“ der einzelnen Zeitreihen be

einflussen die (Kreuz-)Korrelationen zwischen den Zeitreihen; und da die Residuen Meßfehler und implizite (nicht gemessene) Einflußgrößen be

inhalten, die ebenfalls seriell korrelieren, können

4 Dynamische Modelle, die diese Annahme fallenlassen, können natürlich nicht nur in der Zeitreihenanalyse, son

dern auch in der Verlaufsdaten- (Ereignis-) und der Panel

analyse eingesetzt werden.

(2)

Helmut Thome: Scheinregressionen, kointegrierte Prozesse und Fehlerkorrekturmodelle 203

sie nicht, wie in den Querschnittanalysen meist vorausgesetzt, als unabhängig voneinander gelten.

Ein besonderer Fall der Autokorrelationsproble

matik liegt vor, wenn Zeitreihen, deren strukturel

le Zusammenhänge man prüfen und modellieren möchte, lokale oder globale Trendverläufe aufwei

sen. Beispiele hierfür liefern die aggregierten Par

teipräferenzen (s. unten, Abb. 5), die Arbeitslo

sendaten (Abb. 4) oder die Einschätzung der allge

meinen wirtschaftlichen Lage (Abb. 3). Aber auch aus anderen Gebieten (z. B. der historischen Kri

minalitätsforschung, der langfristigen Entwicklung wohlfahrtsstaatlicher Indikatoren) liegen Zeitrei

hen mit derartigen Verlaufsformen vor. Wenn strukturelle Zusammenhänge zwischen verschie

denen Zeitreihen untersucht werden sollen, müs

sen die Trendkomponenten adäquat berücksich

tigt werden. Dies geschieht häufig nicht. Wenn man das Problem nicht einfach ignoriert, werden routinemäßig zwei Strategien verfolgt, ohne ihre Anwendungsbedingungen vorher zu klären: (1) Die Daten werden mit Hilfe irgendeiner Polynom

funktion „trendbereinigt“, oder - was auf dasselbe hinausläuft - der Zeitindex wird in irgendeiner Form als „Kontrollvariable“ in die Regressions

gleichung mit aufgenommen. (2) Man modelliert den statischen oder dynamischen Zusammenhang nicht für die ursprünglichen Niveau-Variablen, sondern für die Veränderungsbeträge, die sich von Zeitpunkt zu Zeitpunkt ergeben. Ignoriert man das Problem oder wählt die erste Strategie, wird man in den meisten Fällen Scheinbeziehungen identifizieren. Wählt man dagegen die zweite Stra

tegie, begibt man sich in die entgegengesetzte Ge

fahr, fälschlicherweise das Fehlen einer Beziehung festzustellen (scheinbare Nicht-Kausalität). In jün

gerer Zeit ist mit den Kointegrations- und Fehler

korrekturmodellen eine dritte Strategie entwickelt worden, mit der sich die Problematik der Nicht- Stationarität der Zeitreihen unter bestimmten Voraussetzungen positiv wenden läßt. Diese Stra

tegie dient nicht nur der Vermeidung der eben an

gesprochenen Fehler; sie eröffnet darüber hinaus die Möglichkeit, eine eventuell vorhandene lang

fristige Gieichgewichtsbeziehung zwischen zwei oder mehr Variablen und die kurzfristige Anpas

sungsdynamik, mit der eine Störung des Gleichge

wichts vom „System“ bearbeitet wird, simultan zu modellieren. Da diese Strategie unter Soziologen noch wenig bekannt ist, soll sie hier anhand eines einfachen Beispiels vorgestellt werden, das den Zusammenhang zwischen ökonomischen Indika

toren und aggregierten Parteipräferenzen betrifft.

In anderen Sachgebieten stellen sich strukturell

identische Analyseaufgaben, die mit der gleichen Methodik bearbeitet werden können. Das Anwen

dungsbeispiel läßt sich jedoch nicht verständlich darstellen, wenn nicht zuvor einige formale Kon

zepte, die motivierende Problemlage und die An

wendungsvoraussetzungen der Methode geklärt werden.

Zunächst werden (in Abschnitt 2) einige Basismo

delle und terminologische Vereinbarungen vorge

stellt, die im folgenden laufend benutzt werden.

Im dritten Abschnitt werden deterministische und stochastische Trendprozesse unterschieden, eine Unterscheidung, die für das Verständnis der

„Scheinregression“ und der Kointegrationsmodel- le fundamental ist. Der vierte Abschnitt bringt eine knappe Einführung in die sog. Einheitswur

zeltests, mit denen Hypothesen über die Stationa- rität oder Nicht-Stationarität einer Zeitreihe bzw.

den deterministischen oder stochastischen Cha

rakter von Trendkomponenten geprüft werden.

Der fünfte Abschnitt erläutert unter dem Stich

wort „Scheinregressionen“ Verzerrungseffekte, die auftreten können, wenn in Regressionsana

lysen Trendkomponenten nicht adäquat berück

sichtigt werden. Im sechsten Abschnitt werden die Kointegrations- und Fehlerkorrekturmodelle im Kontext des bereits erwähnten Anwendungsbei

spiels vorgestellt. Der siebte Abschnitt faßt die zentralen Überlegungen mit einigen zusätzlichen Hinweisen zusammen.

2. Basismodelle und Notationen

Es ist natürlich nicht möglich, in diesem Abschnitt in die Grundlagen der Zeitreihenanalyse einzufüh

ren5. Es sollen lediglich einige Basismodelle und Notationen erläutert werden, ohne die die folgen

den Abschnitte nicht verständlich sind.

Beobachtete Zeitreihen werden als Realisationen stochastischer Prozesse betrachtet. Die Basismo

delle setzen voraus, daß diese Prozesse „schwach stationär“, d.h. die beiden ersten Momente (Mit

telwerte und Varianzen/Kovarianzen) des erzeu

genden Prozesses zeitlich stabil sind: Erwartungs

wert (Niveau) und Varianz der realisierbaren Wer

te sind für alle Beobachtungszeitpunkte konstant;

das Maß der Abhängigkeit zweier Werte (ihre Au

tokovarianz) ist lediglich abhängig von dem zeitli

chen Abstand ihrer Realisationen, nicht von der

5 Einführungen in die univariate Zeitreihenanalyse bietet Thome (1992a; 1994); zur dynamischen Regressionsana

lyse siehe Thome (1992b).

(3)

2 0 4 Zeitschrift für Soziologie, Jg. 26, Heft 3, Juni 1997, S. 202-221

historischen Zeit. Stationäre Prozesse lassen sich in sog. ARMA(p,q)-Modellen „sparsam“ mit Hilfe einer Kombination von autoregressiven und

„moving-average“ Komponenten darstellen (s.

Box/Jenkins 1976):

yt - <1hy(~\ - • • • - $Py,-P = c + at - ,... - (2-1) {YJ mit t = l,2,...,n bezeichne eine stationäre Zeitreihe; c sei eine Konstante und {at} eine Folge von Zufallsgrößen (random shocks), die identisch und unabhängig voneinander normalverteilt sind mit dem Erwartungswert E(a,) = 0 und der Varianz var (at) = a 2. Wenn alle 0-Gewichte, nicht aber alle

<|>-Gewichte in (2-1) gleich Null gesetzt sind, han

delt es sich um einen autoregressiven Prozeß p-ter Ordnung: AR(p) oder ARMA(p,0); falls alle 0- Gewichte, nicht aber alle 0-Gewichte gleich Null gesetzt sind, handelt es sich um einen „moving- average“ Prozeß q-Xtr Ordnung: MA(q) oder AR- MA(0,q); wenn sämtliche $- und 0-Gewichte gleich Null sind, spricht man von „weißem Rau

schen“ oder einem white-noise Prozeß. In der uni- variaten Analyse versucht man, aus der empiri

schen Autokorrelationsfunktion (und anderen Musterfunktionen) die p- und ^-Parameter, also die Anzahl der benötigten <|>- und 0-Gewichte zu bestimmen („Modellidentifikation“), sie mit ei

nem geeigneten Verfahren zu schätzen und das ge

schätzte Modell anhand bestimmter Kriterien auf seine Adäquanz zu prüfen („Modelldiagnose“).

Gleichung (2-1) läßt sich mathematisch leichter handhaben, wenn der „Backshift“-Operator B (oder „Lag“-Operator L) eingeführt wird, der wie folgt definiert ist:

BmYt = Y t_m , m = 1,2,... (2-2) s ° = i

Bc = c , c = Konstante

Gleichung (2-1) kann nun wie folgt geschrieben werden:

(1 - - «fcß2 - . . . - = c + (2-3) (1 - 0,ß - 02ß2 - . . . - %Bq)a,

Mit Hilfe des Verschiebe-Operators B läßt sich auch die Differenzenbildung darstellen, ein häufig angewandtes Verfahren der Trendbereinigung, das in Abschnitt 3 diskutiert wird:

= >V, = (1 - B)y, s Ay, (2 -4 )

Unter Umständen muß die Differenzenreihe wt nochmals „differenziert“ werden, bevor Stationa- rität erreicht wird. Die mehrfache Differenzenbil

dung (ihr Grad d) ist durch das Exponieren des Differenzenoperators darstellbar. Bei zweifacher Differenzenbildung, d - 2, erhalten wir somit:

Aiv, = [(>’t-y,-i) - (y,-i->'i-2)l = (1 - Bf y, S A2y, (2-5) Die „Inversion“ der Differenzenbildung, das schrittweise Summieren der Differenzenbeträge, wodurch die ursprüngliche Zeitreihe wiederherge

stellt wird, läßt sich nun sehr einfach mit Hilfe ei

nes negativen Exponenten (-d) des Differenzen

operators darstellen, im Falle von d - 1:

(1 - B f 1 = (1 + £ + £ 2...) = £ # (2-6)

7=0 .o

(1 - a£)_1 = (1 + a B + a2B2 + ...) = X aI& ; 0 < a < 1

7=0

Indem man B wie eine algebraische Größe behan

delt, lassen sich die Nullstellen („Wurzeln“) der Lag-Polynome in (2-1) berechnen, die Informatio

nen über wichtige Prozeßcharakteristiken enthal

ten. Wenn die Nullstellen des AR-Polynoms alle au

ßerhalb des Einheitskreises liegen, ist der Prozeß schwach stationär im oben definierten Sinne. Reine MA-Prozesse sind stets stationär; dennoch wird auch hier verlangt, daß die Nullstellen des Polynoms (1 - 0tB - ... -0qBq) außerhalb des Einheitskreises liegen, um die sog. Invertibilität des Prozesses zu ge

währleisten. Diese Eigenschaft wird benötigt, um MA-Prozesse in AR-Prozesse „übersetzen“ zu kön

nen und um eine eindeutige Zuordnung von Prozeß

struktur und Autokorrelationsfunktion sicherzu

stellen. Der Differenzenoperator (1-B) läßt sich als ein spezielles autoregressives Polynom mit dem Ko

effizienten <|) = 1 interpretieren:

(1 - B) y , = at (2-7)

yt = yt-\ + at

Ein autoregressiver Prozeß 1. Ordnung mit einem solchen Koeffizienten stellt einen Grenzfall dar;

die Nullstelle dieses Polynoms liegt exakt auf dem Einheitskreis: (1-B) = 0 => B = l.M it Hilfe eines solchen Lag-Polynoms lassen sich, wie wir in Ab

schnitt 3 noch näher erläutern werden, stochasti

sche Trendkomponenten darstellen. Derartige Prozesse bezeichnet man auch als „grenzstationä

re“ oder „homogen nicht-stationäre“ Prozesse.

Wenn die Zeitreihe durch d-fache Differenzenbil

dung stationär „gemacht“ wird, spricht man - in Anspielung auf das Summieren der Differenzen

beträge - auch von „integrierten“ Prozessen „d-ter Ordnung“ oder kurz von /(d)-Prozessen.

3. Deterministische und stochastische Trendmodelle

Zunächst muß die Unterscheidung von determini

stischen und stochastischen Trendverläufen ge-

(4)

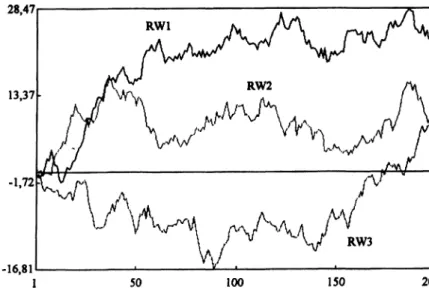
Abb. 1 Drei simulierte

Random- Walk-P ^rozesse.

klärt werden, weil sonst weder der volle Umfang der Probleme der Scheinregression noch die Vor

aussetzungen der Konstruktion von Kointegra- tionsmodellen zu verstehen sind.

Der Begriff des Trends ist allgemein nur vage defi

niert als „eine langfristige systematische Verände

rung des mittleren Niveaus der Zeitreihe“ (Schlitt- gen/Streitberg 1989: 9). Der Substanzwissenschaft

ler muß anhand eines konkreten Gegenstands fest

legen, wie er dieses Konzept präzisieren und ver

wenden möchte. Die Statistik bietet zur formalen Spezifikation zwei (noch weiter differenzierbare) Modellklassen und einige Auswahlkriterien an.

Deterministische Trendmodelle fassen den Trend als eine Funktion der Zeit auf, bspw. in Form eines Polynoms m-ten Grades. Die Zeitreihe selbst läßt sich dann durch folgende Gleichung darstellen

yt ~ ßo + ßl* + ß2*2 + • • • + ßm*W⁺ ^t = 1*2,. • -(3-1) wobei ut eine stationäre Komponente bezeichnen soll, die um den Trend zentriert ist. Ein unter So

zialwissenschaftlern beliebter Sonderfall ist der li

neare Trend mit m = 1. Die Koeffizienten ß0, .. .,ßm können im Prinzip mittels Regressionsanalyse be

stimmt werden, wobei die Angemessenheit des üb

lichen Kleinstquadratverfahrens an die bekannten Bedingungen über die Verteilungseigenschaften der Restgröße ut gebunden ist. Eine „trendberei

nigte“ Zeitreihe läßt sich sodann mittels Subtrak

tion ermitteln. Die Schätzalgorithmen können bei anderen Zeitfunktionen wie z. B. der Exponential

funktion oder der logistischen Funktion (zur Dar

stellung von Wachstumskurven) komplexer wer

den, sind jedoch ebenso wenig Gegenstand dieses

Artikels wie die konzeptuell und methodisch schwierige Trennung von Trend und langen Zy

klen.6

Zur Erläuterung stochastischer Trendmodelle be

trachten wir zunächst einen Sonderfall, den sog.

einfachen Random-Walk-Prozeß (RWP), den wir schon in Abschnitt 2 eingeführt hatten:

y, = y,~\ + a, (3-2)

yt -y,~\ = a,

Nimmt man für diesen Prozeß einen willkürlichen Startwert von y0 an, so erhält man rekursiv

y i = y 0 + «i (3-2a)

yz = y0 + a\+ a2

t

y, = y« + X at i=l

Der Erwartungswert ist somit E(y,) = y0, wenn E («/) = 0. Ist ein späterer Wert yt erst einmal beobachtet, liefert er den bedingten Erwartungs

wert für einen beliebigen Prognosehorizont s:

E( Yt +51 yd = Tms = 1 *2,... Der Prozeß ist aber nicht

stationär, denn die Varianz wächst mit der Zeit: Da die random shocks als unabhängig voneinander vor

ausgesetzt werden, ergibt sich die Varianz der Sum

me aus der Summe der Varianzen g2 für die einzel

nen Zufallsvariablen at in Gleichung (3-2a) Var(Y,) = = t o 2

Das heißt, mit t -» °o wächst die Varianz des Pro

zesses ins Unendliche, sie ist nicht begrenzt. Der

6 Zum letzteren siehe Thome/Rahlf (1996).

(5)

206 Zeitschrift für Soziologie, Jg. 26, Heft 3, Juni 1997, S. 202-221

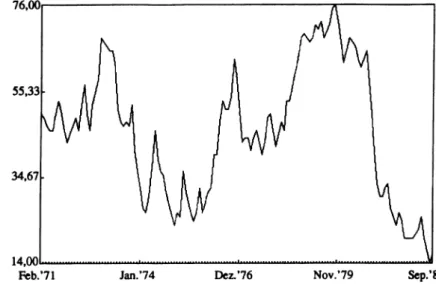
A b b .2 Vergleich Random- Walk mit Drift und trend

stationärer Prozeß.

RWD: yt = 0,2 + yM + at TSP: yt = 0,2 • t + at

Prozeß pendelt unregelmäßig hin und her und kann für längere Zeit auch eine dominant aufstei

gende oder abfallende Richtung verfolgen. Inner

halb begrenzter Beobachtungsperioden kann so

mit der Eindruck entstehen, es läge ein determini

stischer Trend oder ein zyklischer Verlauf vor.

Wie die Realisationen in Abb. 1 zeigen, hat der RWP - anders als ein stationärer Prozeß -nur eine schwache Affinität zu seinem Erwartungswert.

Theoretisch wiederholt er erst im Unendlichen ir

gendeinen Wert, den er zuvor schon einmal reali

siert hat (Mills 1990: 99). Akkumulierte Gewinn

summen beim Lotteriespiel und Preisbewegungen auf spekulativen Märkten folgen häufig einer sol

chen Prozeßdynamik: zu jedem Zeitpunkt beginnt ein neues „Spiel“. Die ständigen Auf- und Ab

wärtsbewegungen mit ihren unregelmäßigen, viel

fachen Richtungswechseln stellen keine „determi

nistische“, sondern „stochastische“ Trendbewe

gungen dar. Sie müssen nicht unbedingt in der „rei

nen“ Form des RWP gemäß Modellgleichung (3-2) realisiert werden, sondern können auch als Ele

ment einer komplexeren Prozeßdynamik auftreten.

Wie wir schon in Abschnitt 2 sahen, ist der RWP (3-2) formal ein autoregressiver Prozeß erster Ordnung mit dem Koeffizienten § = 1. Das autore

gressive Polynom (1-<|>B) = (1-B) hat die Wurzel (Nullstelle) B = 1; der Prozeß ist damit im Sinne der im vorigen Abschnitt referierten Stationari- tätsdefinition nicht-stationär, er ist ein sog. Ein

heitswurzel- (Unit-Root)-Prozeß. Solche Prozesse sind dadurch gekennzeichnet, daß sie zwar stocha

stische Trendverläufe aufweisen, aber durch Diffe

renzenbildung in stationäre Prozesse überführt werden können.7 Man spricht deshalb auch von

„differenzenstationären“ im Unterschied zu

„trendstationären“ Prozessen, DSP statt TSP Werden stochastische und deterministische Trend

prozesse nicht korrekt identifiziert und werden demgemäß inadäquate Verfahren der Trendberei

nigung angewandt, können daraus substantiell feh

lerhafte Interpretationen folgen (s. unten).

Bevor wir darauf näher eingehen, soll noch das er

weiterte random walk Modell, der random walk with drift (RWD), vorgestellt werden:

y, = yt-i + H + a, (3-4)

Er unterscheidet sich von dem Modell (3-2) ledig

lich durch die Konstante p. Sie besagt, daß die Zeitreihe in jedem Intervall durchschnittlich um den Betrag p ansteigt. Bei einem willkürlichen Startwert von ^{y = y0}ergibt sich ein Erwartungswert

£(Y,) = y0 + r n (3-5)

Die Varianz ist weiterhin to 2, strebt also gegen un

endlich. Die Konstante p bezeichnet man als drift- Parameter, der eine deterministische Komponente in Form eines linearen Trends (mit p als Steigungs

koeffizient) in den Prozeß einführt: die Zeitreihe entfernt sich - unter fortlaufenden stochastischen

7 Ein autoregressiver Prozeß mit <|> > 1 nimmt einen expo

nentiell ansteigenden Verlauf an und kann nicht durch Differenzenbildung, auch nicht durch wiederholte D iffe

renzbildung, in einen stationären Prozeß überführt wer

den. Formal ist das dadurch erkennbar, daß die Lösung der charakteristischen Gleichung in B kleiner als 1 ist, z.B.: ( 1 - 1 . 2 B) = 0 => B = 0.83.

(6)

Schwankungen - zunehmend von ihrem Ur

sprungsort. Der dr//if-Parameter beeinflußt den Reihenverlauf um so stärker, je größer der Quo

tient |i/a2a . Aber auch dieser RWD läßt sich durch (einfache) Differenzenbildung in eine stationäre Reihe transformieren; aus Gleichung (3-4) ergibt sich unmittelbar: (1-B )yt = p + at

Die simulierten Realisationen des RWD in Abb. 2 zeigen, daß sie nur eine geringe Affinität zu der mit dem drift-Parameter jn gesetzten Trendlinie aufweisen; die durch die Zufallsereignisse ( a j an

gestoßenen lokalen Trends pendeln fortlaufend und unregelmäßig oberhalb und unterhalb dieser Durchschnittsgröße hin und her. Jedes Zufalls

ereignis at * 0 setzt die Trendlinie (den Prognose

pfad) auf eine neue Spur, die parallel zu den voran

gegangenen verläuft, aber von einem neuen Ordi

natenabschnitt ausgeht.8 Der bedingte Erwar

tungswert ergibt sich aus

E ( Y M = y t + s-VL (3-6)

t

= V0 + X a i + 5 • f l i = l

Das heißt, er ist durch die Summe der vorangegan

genen Zufallsereignisse mit bestimmt. Folglich wächst der Prognosefehler mit der Länge des Pro

gnosehorizonts ad infinitum. Im deterministischen Trendmodell (3-1) dagegen ist die langfristige Pro

gnose identisch mit dem Trendwert, gegenwärtige und vergangene Ereignisse liefern keine zusätzli

chen Informationen; der mittlere quadrierte Pro

gnosefehler konvergiert gegen die Varianz der sta

tionären Restkomponente.

Was passiert, wenn ein differenzenstationärer Pro

zeß (DSP) nicht durch Differenzenbildung, son

dern mit Hilfe einer Polynomfunktion trendberei

nigt wird, deren Parameter in einer „gewöhnli

chen“ (OLS-)Regression geschätzt worden sind?

Diese Frage haben u. a. Nelson/Kang (1981; 1984) mit Hilfe von Simulationsstudien untersucht. Die wichtigsten Ergebnisse lassen sich wie folgt zusam

menfassen:9

1. Wenn die Reihe von einem random walk ohne drift erzeugt wurde, führt eine OLS-Regression der Reihe auf den Zeitindex t zu einem durch

schnittlichen Determinationskoeffizienten nicht von r2 = 0, sondern von r 2 = 0.44, und zwar unab

8 Zu Einzelheiten siehe Hamilton (1994: 435 ff.), Mills (1990: 92 ff., 199ff.), Nelson/Plosser (1982), Raffalovich (1994).

9 Vergl. Maddala (1992: 261) und Mills (1990: 201). Ana

lytische Begründungen für diese Ergebnisse liefern Dur- Iauf/Phillips (1988).

hängig von dem Stichprobenumfang (d.h. der Län

ge der beobachteten Zeitreihe). Falls der erzeu

gende Prozeß einen drift einschließt, wird der De

terminationskoeffizient ebenfalls zu hoch ge

schätzt; die Schätzung tendiert mit zunehmendem Stichprobenumfang gegen 1.

2. Die Signifikanztests (mit Students /-Statistik) werden unzuverlässig. Im Falle eines random walk ohne drift wurde die korrekte Nullhypothese, der Steigungsparameter für den Zeitindex sei ß = 0, bei einem nominellen Fehlerrisiko von 5% in 87%

der Fälle abgelehnt (Quote ermittelt für einen Stichprobenumfang von 100).10 * * Diese besondere Form der „Schein-Regression“ führt zu autokorre

lierten Fehlern. Die Wahrscheinlichkeit für eine fälschliche Zurückweisung der Nullhypothese wurde aber nur geringfügig auf 73% gesenkt, wenn der Schätzalgorithmus eine Fehler-Autore

gression 1. Ordnung berücksichtigte. Dieses Er

gebnis bestätigt „the importance of correctly iden

tifying the behavior of error processes prior (Her

vorhebung, H. T.) to engaging in significance te

sting“ (Durlauf/Phillips 1988: 1349).

3. Die durchschnittliche Höhe der artifiziellen Autokorrelationen der Residualreihe (der trend

bereinigten Daten eines random walk) hängt vom Stichprobenumfang n ab. Der Autokorrelations

koeffizient zum lag 1 beträgt ca. (1-10/n). Außer

dem zeigt das Muster der geschätzten Autokorre

lationen eine zyklische Schwingung mit einer Pe

riode von (2/3)n, was zu der Annahme verleiten könnte, tatsächlich einen zyklischen Prozeß ent

deckt zu haben.11

Es kann also in mehreren Hinsichten zu gravieren

den Fehlschlüssen kommen, wenn man versucht, aus einem differenzenstationären Prozeß einen mutmaßlichen Trend nicht durch Differenzenbil

dung, sondern mit Hilfe eines trendstationären Modells zu eliminieren. Im allgemeinen sind weni

ger fatale Konsequenzen zu erwarten, wenn ein (wahrer) trendstationärer Prozeß durch Differen

zenbildung transformiert wird (Maddala 1992:261 f.). Die Koeffizienten des Trendpolynoms können nach der Differenzenbildung unverzerrt mit Hilfe der üblichen Kleinstquadratmethode ge

schätzt werden. Im Falle eines linearen Trends z.

B. wird der Steigungskoeffizient zum Ordinaten

abschnitt der einfach differenzierten Reihe. Al

10 D ieses Ergebnis stellte sich ein, obwohl der Schätzer ß im Limit gegen Null konvergiert (Durlauf/Phillips 1988).

11 Eine Diskussion dieser Problematik findet sich in Tho- me/Rahlf (1996).

(7)

208 Zeitschrift für Soziologie, Jg. 26, Heft 3, Juni 1997, S. 202-221

lerdings wird durch die Differenzenbildung der Fehlerterm zu einem nicht-invertierbaren MA- Prozeß,12 was zu ineffizienten Schätzungen (er

höhten Standardfehlern) führt. Dieses Problem kann dadurch gemildert werden, daß die Autokor

relation der Fehler simultan in der Schätzglei

chung mit berücksichtigt wird (s. Mills 1990: 202).

Die Differenzenbildung ist aber durchaus nicht zu empfehlen, wenn (a) eine nicht-integrierte Reihe eine zyklische Komponente enthält oder wenn (b) die strukturelle Beziehung zwischen Zeitreihen modelliert werden soll, die kointegriert sind (s.

Abschnitt 6).

Bevor wir uns mit der Modellierung struktureller Beziehungen zwischen zwei (oder mehreren) nicht-stationären Zeitreihen beschäftigen, sollen Testverfahren vorgestellt werden, die entwickelt worden sind, um zuverlässiger zwischen stationä

ren und nicht-stationären und - im Falle der Nichtstationarität - zwischen DS- und TS-Prozes- sen unterscheiden zu können.

4. Einheitswurzeltests

Die Einheitswurzeltests sind in vielerlei Varianten entwickelt und in Hunderten von Artikeln disku

tiert worden. In dieser knappen Einführung sollen nur die Standard-Tests, die Dickey und Fuller (Fuller 1976; Dickey/Fuller 1979; Dickey/Fuller 1981) ausgearbeitet haben, vorgestellt werden. Bei der Anwendung all dieser Tests ist man mit einem grundsätzlichen Problem konfrontiert: Jede endli

che Reihe von n Realisationen, die tatsächlich von einem Einheitswurzelprozeß generiert wurde (bspw. einem AR(l)-Prozeß mit 0 = 1 ) , läßt sich ebenso gut durch ein stationäres Prozeßmodell darstellen, in dem die entscheidenden Koeffizien

ten eine Wurzel in der Nähe von 1 implizieren, z. B. 0 = 0.999 (s. Hamilton 1994: 444 ff.). Es gibt also stets lokale Alternativen, denen gegenüber der Test praktisch keine Trennschärfe hat - dies gilt im Prinzip für fast alle statistischen Tests. Bei kurzen Zeitreihen (Daumenregel: n < 100) ist die Trennschärfe aber auch gegenüber größeren Ab

weichungen von der Nullhypothese so gering, daß Kritiker die Einheitswurzeltests in diesen Fällen grundsätzlich für nicht sinnvoll einsetzbar halten (s. z.B. DeJong et al. 1992). Letztlich geht es um

12 D ieses Problem entsteht nicht, wenn der Prozeß so

wohl ein (deterministisches) Trendpolynom zum Grad m als auch eine ARIM A-Komponente mit d Einheitswur

zeln enhält, solange m < d (s. Mills 1990: 202).

das relative Gewicht von Alpha- und Beta-Fehlern sowie von Konsistenz und Effizienz der Schätzun

gen. „The goal of unit root tests is to find a parsi

monious representation that gives a reasonable ap

proximation to the true process, as opposed to de

termining whether or not the true process is liter

ally 7(1) (Hamilton 1994: 516).13

Der eben erwähnte Dickey/Fuller-Test (DF-Test) ist für zwei unterschiedliche Situationen konzipiert worden: (a) für unabhängige Modell-Residuen („einfacher“ DF-Test), (b) für autokorrelierte Re

siduen (erweiterter, augmented Test: ADF-Test).

Beide Male wird eine Nullhypothese, wonach der vorliegende Prozeß differenzenstationär sei, gegen die Alternativhypothese, er sei stationär oder trendstationär, getestet. Zur Durchführung des Tests in der „einfachen“ Version haben Dickey und Fuller drei elementare Schätzgleichungen vor

geschlagen, deren Parameter nach dem üblichen (OLS) Regressionsverfahren geschätzt werden:14

y, = PoJ^r-1 + u, (4-la)

y, = ah + phy,_x +u, (4-1 b) y, = cc, + y j + pcy,_i + u, (4-lc) Es wird angenommen, daß die Residuen unabhän

gig und identisch normalverteilt sind, ut ~ i.i.d. N{0, e r) 15 * Hie Alternativhypothese impliziert die An

nahme p <1, die Nullhypothese die Annahme p = 1.

Unter der Nullhypothese sind die OLS-Schätzer p aber nicht normalverteilt. Ihre asymptotischen Ei

genschaften sind davon abhängig, ob die Schätz

gleichung eine Konstante oder einen Zeitindex als Regressor enthält und ob der unterstellte wahre

13 Eine weitergehende Problematisierung dieses Test- Ansatzes muß hier unterbleiben; auch technische Einzel

heiten können nicht abgehandelt werden. Eine ausführli

che Kritik mit Blick auf wirtschaftshistorische Analysen enthält - mit vielen Literaturhinweisen - die Habilita

tionsschrift von R. Metz (1995); siehe auch die knappen Bemerkungen in Maddala (1992: 584 ff.).

14 Die Schätzgleichungen werden häufig auch in einer an

deren Form eingesetzt, analog zu (4-la) z.B . mit: Ayt = pyt_i + ut. D ie Nullhypothese der Nichtstationarität ist dann p = 0. Bei stationären Reihen müßte p < 0 sein, da relativ hohen y-Werten der Tendenz nach relativ niedrige y-Werte folgen. (Der Regressionsparameter wird in die

sem Kontext häufig mit p bezeichnet, da er bei einem A R (1) Prozeß mit dem Korrelationskoeffizienten iden

tisch ist.)

15 Unter dieser Voraussetzung geben Fuller (1976) und Dickey/Fuller (1981) auf der Basis von Monte-Carlo-Ex- perimenten die Verteilungen von ß für kleine Stichpro

ben. Im Falle großer Stichproben sind sie auch gültig, wenn die Fehler nicht normal-verteilt sind (s. Hamilton 1994: 502)

(8)

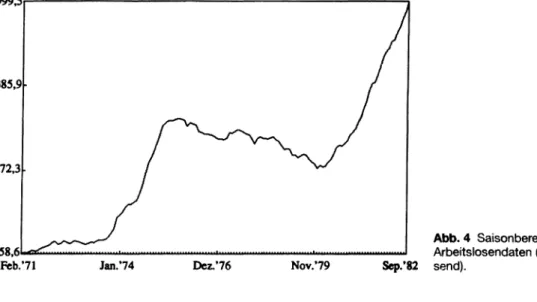
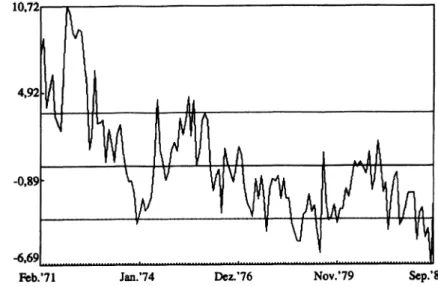
Abb. 3 Aggregierte Ein

schätzung der allgemeinen wirtschaftlichen Lage.

Prozeß einen drift term enthält oder nicht (Hamilton 1994:501 f.). Dickey (1976) und Dickey/Fuller (1981) haben in Monte-Carlo-Experimenten die Verteilun

gen von p unter verschiedenen Nullhypothesen (un

terstellten „wahren Prozessen“) ermittelt; die kriti

schen Werte für unterschiedliche Signifikanzniveaus sind in Tabellenform in verschiedenen Publikationen immer wieder reproduziert worden (so bspw. in Ha

milton 1994; Banerjee et al. 1993).

Die Nullhypothese des einfachen RWP kann so

wohl mit der Schätzgleichung (4-1 a) als auch mit der Schätzgleichung (4-1 b) überprüft werden. In der Regel wählt man Gleichung (4-lb), um gegen

über der Alternativhypothese möglichst „fair“ zu sein (Hamilton 1994: 501; Banerjee et al. 1993:

100ff.); denn das alternative AR-Modell wird zur Repräsentation einer beobachteten Zeitreihe in den meisten Fällen einen konstanten Term a * 0 benötigen.

In einem ersten Beispiel wollen wir mit Hilfe die

ser Testgleichung prüfen, ob die in Abb. (3) wie

dergegebene Reihe „Einschätzungen zur allgemei

nen wirtschaftlichen Lage“ (AWL) 16 differenzen

stationär ist.

16 Prozentanteil derer, die die wirtschaftliche Lage als

„gut“ oder „sehr gut“ einschätzen. D iese Zeitreihe wurde mir von Prof. G. Kirchgässner mit Genehmigung des Bun

despresseamtes zur Verfügung gestellt. Sämtliche Berech

nungen wurden, wenn nichts anders vermerkt ist, mit dem Programmpaket MICROFIT® 3.0 (s. Pesaran/Pesaran 1991) durchgeführt. Für den ADF-Test liefert dieses Pro

gramm auch die kritischen Werte auf dem 5-Prozent-Ni- veau; für andere Niveaus müssen die erwähnten Tabellen konsultiert werden.

Die OLS-Schätzung gemäß Gleichung (4-lb) führt zu folgenden Ergebnissen (Standardfehler in Klammern)

AW Lt = .638 + .98 AW Lt_x + u, (4-2) (1.047) (.0218)

Die Nullhypothese p = 1 wird gegen die Alterna

tivhypothese p < 1 in gewohnter Weise getestet, in

dem die Differenz (p - E(p)) ins Verhältnis zu dem Standardfehler des geschätzten Koeffizienten ge

setzt wird. Da sie aber, wie erwähnt, nicht Students /-Verteilung folgt, bezeichnet man diese Teststati

stik mit x. In unserem Beispiel erhalten wir x=

(0.98 - 1)/0.0218 = -0.91. Laut Füller-Tabelle ist der kritische Wert für diese Stichprobengröße mit -2.89 für das 5%-Signifikanzniveau und mit -2.58 für das 10% -Signifikanzniveau gegeben. Das be

deutet, die Nullhypothese ist nicht zurückzuwei

sen. Die allgemeinen wirtschaftlichen Erwartun

gen sind durch stochastische Trendverläufe ge

kennzeichnet; sie sind ein integrierter Prozeß 1. Ordnung,17 abgekürzt 7(1).

In einem zweiten Beispiel betrachten wir die saiso

nal bereinigte Reihe der monatlichen Arbeits

losenzahlen (in Tausend) der BRD, ebenfalls für den Zeitraum von Febr. 1971 bis Dez. 1982 (s. Abb.4).18

17 An diesem Ergebnis ändert sich nichts, wenn wir eine autoregressive Fehlerstruktur berücksichtigen (s. unten).

18 D ie Saisonbereinigung wurde mit SPSS/PC-DOS nach dem Verfahren der gleitenden Mittelwerte durchgeführt (additives Modell für wurzeltransformierte Daten mit nachfolgender Rücktransformation). Zum Verfahren sie

he Thome (1992a); siehe auch Fußnote 36.

(9)

21 0 Zeitschrift für Soziologie, Jg. 26, Heft 3, Juni 1997, S. 202-221

Abb. 4 Saisonbereinigte Arbeitslosendaten (in Tau

send).

Die empirische Verlaufsform der Reihe wie auch substantielle Erwägungen sprechen gegen die Al

ternativhypothese, dieser Prozeß sei stationär.

Folglich testen wir die Nullhypothese eines diffe

renzenstationären Prozesses mit drift gegen die Hypothese eines trendstationären Prozesses. In diesem Beispiel ist es jedoch nicht sinnvoll, Unab

hängigkeit der Residuen im Testmodell (4-lc) zu unterstellen. Zur Saisonbereinigung wurde ein Verfahren angewandt (s. Fußnote 18), das eine konstante Saisonfigur unterstellt, eine wenig reali

stische Annahme. Wir müssen also davon ausge

hen, daß die auf diese Weise adjustierte Reihe eine serielle Korrelation über zwölf Monatsintervalle aufweist. Deshalb können wir nicht Gleichung (4-lc), sondern müssen die erweiterte Schätzglei

chung19 des Augmented Dickey-Fuller-Tests (ADF-Test) anwenden:

y, = a + yt + py,_, + ü>,(AyM) + (^(Ay,_2) (4-3) + ... + o>f,-i(Ay,_;,+1) +

u,

Die OLS-Schätzung mit p=12 führt zu folgenden Ergebnissen:

19 Zur Herleitung dieser Schätzgleichung und Diskussion alternativer Vorgehensweisen siehe Hamilton (1994:

504 ff., 517 ff.). Gleichung (4-3) resultiert aus einer Umfor

mung der Gleichung yt = a + ßt + «hy^, + <feyt-2 + • • • + 4>PYt-p + ut. Es ist gängige Praxis, auch nicht-signifikante Terme yt_k mit 0 < k < p auf der rechten Seite der Schätzgleichung mit zu berücksichtigen. Bei vorgegebener Saisonalität spricht allerdings nichts dagegen, die vorgelagerten Ver

zögerungsterme zu eliminieren. Zur Bestimmung eines adäquaten Verzögerungsparameters p siehe Hamilton (1994: 530).

ARBLO( = 3.937 + .2925/ + .971 \A R B LO t. x (4-4) (3.898) (.0956) (.00954)

+ 364AARBLOt_{ + A93AARBLOt_2 +

(.869) (.0925)

. .. + Al$AARBLOt_n (.0917)

Für den Test der Nullhypothese H0: p = 1 erhalten wir in gleicher Weise wie im vorigen Beispiel x = -3.03. Der kritische Wert ist laut Dickey/Fuller-Ta- belle -3.44 für das 5% -und -3.15 für das 10%-Si

gnifikanzniveau. Die Nullhypothese wird folglich nicht zurückgewiesen, die Arbeitslosenzahlen scheinen eine stochastische Trendkomponente zu enthalten. Um eine deterministische Trendkompo

nente ausschließen zu können, müssen wir aber auch noch die verbundene Hypothese testen: y = 0 und p = l.D as geschieht analog zu dem üblichen F-Test; die entsprechende Teststatistik wird jedoch mit O bezeichnet, weil sie unter der Nullhypothese nicht F-verteilt ist. Um die Teststatistik zu ermit

teln, muß das gemäß Nullhypothese restringierte Modell geschätzt werden - mit folgenden Ergeb

nissen:

ARBLO, - ARBLO t_x = (4-5)

2.468 + 399AARBLt_l + . .. + A01AARBLt.u + ut

(2.091) (.089) (.091)

Daß auf der linken Seite der Differenzenbetrag (yt - yt_i) steht, folgt aus der Hypothese p = 1. Die Teststatistik kann nun nach der üblichen Formel berechnet werden:

4> =(RSSr - RSSg/m (54647 - 50627) /2 „

RSSe/(n-k) ~ 50627/124 “ 4’yZ (4-6) Dabei bezeichnen RSSr und RSSe Fehlerquadrat

summen (Residual Sum o f Squares) des restrin

(10)

gierten bzw. des erweiterten Modells, m und (n-k) die jeweiligen Freiheitsgrade. Die von Dickey und Fuller ermittelten kritischen Werte für die Ableh

nung der Nullhypothese sind = 6,45 für das 5%- Signifikanzniveau und d>= 5,45 für das 10%-Ni

veau. Die Nullhypothese wird somit beibehalten;

die Arbeitslosenreihe enthält keine deterministi

sche Trendkomponente im Sinne eines TSP. Da auch die Konstante ä = 2.468 in Gleichung (4-5) nicht signifikant von Null abweicht, kann eine dn/r-Komponente ebenfalls ausgeschlossen wer

den.20 Die Arbeitslosen-Reihe (s. Abb.4) ändert im Beobachtungszeitraum nicht nur ihr Niveau, sondern auch ihre Trendneigungen, sie könnte also auch einen integrierten Prozeß zweiter Ordnung - 1(2) - darstellen. In diesem Falle wären die ersten Differenzen nicht stationär, sondern repräsentier

ten einen /(l)-Prozeß. Eine solche Annahme wird durch die relativ langsam abfallende Autokorrela

tionsfunktion der ersten Differenzen (hier nicht gezeigt) gestützt; allerdings liegt der Autokorrela

tionskoeffizient bei Lag 1 mit ß = 0.63 deutlich un

ter l.21 Wir wollen nun die Nullhypothese des 7(1)- Prozesses für die ersten Differenzen gegen die Al

ternativhypothese eines stationären AR(p)-Pro- zesses testen. Die Partielle Autokorrelationsfunk

tion der Differenzenreihe deutet auf einen autore

gressiven Prozeß zweiter Ordnung hin (p=2), so daß wir folgende Testgleichung schätzen

AARBLt = (4-7)

3.172 + .13SAARBLt.x - 266A2A R B L t_x + ut (1.967) (.077) (.087)

Daraus ergibt sich die Teststatistik x = (.738 - l)/.011 = -3.40 Dieser Betrag liegt unterhalb des kritischen Wertes von -2.88 für das 5%-Signifi

kanzniveau. Die Nullhypothese des Vorliegens ei

ner Einheitswurzel in der Differenzenreihe kann somit zurückgewiesen werden. Wir gehen also da

von aus, daß die saisonal bereinigten Arbeitslosen

daten einen integrierten Prozeß erster Ordnung darstellen.22

20 Da in Gleichung (4-5) auf der linken Seite die Differen

zenbeträge stehen, p = 1 fixiert ist und nicht geschätzt wird, sind für die Schätzer dieser Gleichung die üblichen t- Tests anwendbar.

21 D ies beweist aber noch nicht das Fehlen einer Einheits

wurzel, s. Box/Jenkins (1976: 200 f.).

22 Schätzungen mit einer AR(12)-Struktur in der Glei

chung (4-7) ergaben ein auf dem 5%-Niveau signifikantes

<S>i2; alle anderen Omegakoeffizienten - außer (fy - waren jedoch nicht signifikant. Ein F-Test und ein Lagrange- Multiplier-Test zeigten, daß das erweiterte Modell gegen

über dem restringierten Modell, = 0 für k=2, .. ..12, die

Die Einheitswurzeltests benötigen wir erneut bei der Einführung der Kointegrationsmodelle in Ab

schnitt 6; deren Konstruktion ist u.a. durch das nun zu behandelnde Problem der Scheinbeziehung im Kontext der Regressionsanalyse motiviert.

5. Das Problem der Scheinregression wurde von Granger/Newbold (1974) unter dem Ti

tel „spurious regression“ in die Diskussion einge

bracht. Der Ausdruck bezieht sich auf den Tatbe

stand, daß in einem Regressionsmodell für nicht

stationäre Zeitreihen auch dann ein signifikanter Steigungskoeffizient geschätzt werden kann, wenn keinerlei strukturelle (kausale) Beziehung zwi

schen den Reihen besteht. Das Problem ist in der ökonometrischen Fachliteratur vor allem im Hin

blick auf differenzenstationäre Prozesse abgehan

delt worden (siehe u. a. Granger/Newbold 1974;

Nelson/Kang 1984; Durlauf/Phillips 1988; Baner- jee et al. 1993:70 ff.), nicht zuletzt deshalb, weil an

genommen wird, daß die meisten ökonomischen Zeitreihen eher dem DSP- als dem TSP-Typ zuzu

rechnen sind (Nelson/Plosser 1982). Dies dürfte erst recht für soziologisch relevante Zeitreihen gelten. Deshalb werde ich mich hier ebenfalls auf diesen Prozeßtyp konzentrieren.23

Ausgangssituation sind zwei einfache, nicht mit

einander korrelierte RWP

yt= yt-1 + u, (5-1)

X , = X,_i + V,

E(u,v,) = 0 V f ; E{u,u,_k) = £(v,v,_*) =

0 V & * 0

Unter diesen Vorausssetzungen führt die Kleinst- quadratschätzung des Regressionsmodells

y, = ßo + ßi*,+ (5-2a)

zu irregulären Ergebnissen. Banerjee et al. (1993:

74 ff.) berichten, daß bei Simulationsstudien mit n

= 100 Realisationen die korrekte Nullhypothese (ßi = 0) in 75% aller Fälle bei einem nominellen Signifikanzniveau von 5% zurückzuweisen war.

Die Ablehnungsquote nahm mit größerem Stich-

Fehlerquadratsumme (RSS) nicht in relevantem Maße verringert. Wie sensibel der Dickey/Fuller-Test gegenüber der Spezifikation der Fehlerstruktur ist, zeigt sich darin, daß die erweiterte Testgleichung zu einem Tau-Wert führ

te, der über dem kritischen Wert des 5%- oder 10%-Signi

fikanzniveaus lag. In diesem Falle wäre die Nullhypothese also beibehalten worden.

23 Strukturbeziehungen zwischen Zeitreihen mit determi

nistischen Trendkomponenten diskutiert Kang (1990).

(11)

21 2 Zeitschrift für Soziologie, Jg. 26, Heft 3, Juni 1997, S. 202-221

probenumfang nicht ab, sondern weiter zu. Eine höhere Integrationsordnung der Prozesse ließ die

se Quote nochmals ansteigen und die Korrela

tionskoeffizienten stark gegen r = ±1 tendieren.

Das Problem ist nicht dadurch lösbar, daß man die Reihen vorgängig mit Hilfe einer Polynomfunk

tion trendbereinigt oder (was auf das gleiche hin

ausläuft) den Zeitindex t in gleicher Potenz als

„Kontrollvariable“ in die Regressionsgleichung einführt:

y, = ßo+ ßi*, + Y,+e, (5-2b)

Nelson/Kang (1984), die die Variante (5-2b) eben

falls in Simulationsstudien durchgespielt haben, kamen bei gleichen Signifikanz-Kriterien zu einer nur geringfügig niedrigeren Ablehnungsquote von 64 % und zu einem durchschnittlichen Determina

tionskoeffizienten von r2 = 0.50.24 Da in der realen Forschungspraxis a priori nicht bekannt ist, ob zwei Reihen strukturell miteinander verbunden sind, eine entsprechende Hypothese erst getestet werden soll, sind bei naiver Anwendung des übli

chen Regressions- und Trendbereinigungsverfah

rens gravierende Fehlschlüsse zu erwarten.

Das Problem der Scheinregression bei integrierten Prozessen kann vermieden werden, wenn die Para

meter des Modells (5-2a) nicht mit den Rohdaten, sondern mit den „differenzierten44 Zeitreihen ge

schätzt werden:

Ay, = Y+ß(Ax,) + w„ M, = e , - € M

Da Ay und AX stationäre Prozesse [1(0)] sind, müssen auch die Residuen (als Linearkombination zweier stationärer Prozesse) stationär sein; (5-3) ist folglich eine „legitime44 Regressionsgleichung.

Die Interpretation des Steigungskoeffizienten ß ist durch die Anwendung des Differenzenoperators A s (1-B) auf beiden Seiten der Gleichung nicht berührt. Macht man die Differenzenbildung durch Aufsummieren über alle beobachteten Zeitpunkte rückgängig,25 kommt man bei y * 0 zur Gleichung

t

3', = >'o + Y'+ß^r + Z u i (5-4)

1=1

die einen Trendterm mit einschließt.26 Wenn die Uj nicht autokorreliert sind, ist die Störgröße in (5-4)

24 D ie korrekte Nullhypothese der Unabhängigkeit von der Zeit, wird sogar in 83 % aller Fälle zurückgewiesen.

25 Formal durch Anwendung des inversen Differenzen

operators (1 -B )1.

26 In analoger Weise kommt man auch von einem univa- riaten random walk zu einer Regressionsgleichung, die den Zeitindex als Regressor einschließt (s. Nelson/Kang 1984: 74). D ie in Abschnitt 3 genannten D efekte einer

ein RWP, siehe Gleichung (3-2a). Es ist bekannt, daß der OLS-Koeffizient ß in Gleichung (5-4) nu

merisch mit dem OLS-Koeffizienten identisch ist, den man erhält, wenn man die vorgängig trendbe

reinigten Reihen regressiert (Lovell 1963), also den Koeffizienten ß in

y, = ßx, + ü, (5-5)

schätzt. (Die mittels Polynomfunktion trendbe

reinigten Reihen sind in (5-5) mit einer Tilde ge

kennzeichnet.) Als „trendbereinigte44 random walks haben Regressor- und Residualvariable die gleiche theoretische Autokorrelationsfunktion (da diese, wie in Abschnitt 3 angemerkt, bei ei

nem trendbereinigten RW nur von der Länge der Zeitreihe abhängig ist). Die Kombination von autokorrelierten Residuen und autokorrelierter Regressorvariable vergrößert den wahren Stan

dardfehler des Steigungskoeffizienten um den Faktor (1 + X pkÄ*), wobei pk die Autokorrela

tion der Residuen und Ä* die Autokorrelation der Regressorvariable zum Lag k bezeichnen. In den OLS-Schätzalgorithmen bleibt dieser Faktor unberücksichtigt. Das heißt, der Standardfehler wird, wenn beide Autokorrelationen das gleiche Vorzeichen haben, unterschätzt, die Ablehnung der Nullhypothese erleichtert. Da die Autokor

relation der trendbereinigten random walks mit der Länge der Zeitreihe zunimmt, wird dieser Fehlschluß um so wahrscheinlicher, je länger die Zeitreihen sind.27 *

Die praktischen Auswirkungen dieser Probleme können gemindert werden, wenn im Schätzalgo

rithmus, etwa nach dem Cochrane-Orcutt-Verfah

ren (s. Kmenta 1986: 298 ff.), zumindest die Auto

korrelation erster Ordnung in den Residuen be

rücksichtigt wird. In den Simulationsstudien von Nelson/Kang (1984: 79 f.) konnte die fälschliche Ablehnung der korrekten Nullhypothese (ßj = 0 in Gleichung (5-2a)) auf eine Quote von 11.3% und

Trendbereinigung integrierter Prozesse mittels einer re

gressionsanalytisch geschätzten Polynomfunktion sind also ebenfalls im Sinne einer „spurious regression“ zu deuten.

27 D ie übliche Verteilungstheorie setzt voraus, daß Stich- proben-Momente gegen einen fixen Populationsparame

ter konvergieren. Nicht-Stationarität der Zeitreihen (so

fern sie nicht explizit modelliert werden kann und folglich nicht aus der Residualreihe eliminiert wird) bedeutet, daß keine fixen Populationsparameter vorliegen und die übli

chen Konvergenztheoreme nicht gelten. Zur Verteilungs

theorie, die in diesem Falle benötigt wird, siehe Phillips (1986); Durlauf/Philipps (1988); Baneijee et al. (1993:

8 6 ff.); Hamilton (1994: 558 ff.).

(12)

bei iterativer Anwendung sogar auf knapp 7% ge

senkt werden.28

Die Probleme können auch gemindert werden, wenn in die Regressionsgleichung verzögerte Ter

me {Yt.j} und {Xhl} als Regressoren in die Glei

chung (5-2) einbezogen werden. Allerdings hat der entsprechende F-Test keine standardmäßige Grenzverteilung (Hamilton 1994: 562). Außerdem ist diese technisch gemeinte Korrektur mathema

tisch äquivalent mit einer substantiellen Neuspezi

fikation des dynamischen Zusammenhangs zwi

schen den beiden Variablen (s. Maddala 1992: 244, 255; Thome 1992b: 90ff.) und deshalb nur zu emp

fehlen, wenn sie inhaltlich begründet werden kann.

Wir haben oben festgestellt, daß die Probleme der Scheinregression mit Hilfe der Differenzenbildung umgangen werden können. Dennoch ist davon ab

zuraten, dieses Verfahren routinemäßig anzuwen

den. Selbst wenn die Zeitreihen, deren strukturel

ler Zusammenhang modelliert werden soll, tat

sächlich integrierte Prozesse sind, kann die Diffe

renzenbildung zu einem fehlspezifizierten Regres

sionsmodell führen, dann nämlich, wenn zwischen den beiden integrierten Prozessen eine langfristige Gleichgewichtsbeziehung besteht; wenn sie, wie man sagt, „kointegriert“ sind. In diesem Falle gibt es eine bessere Modellierungsstrategie, die im fol

genden Abschnitt vorgestellt werden soll.

6. Kointegrierte Prozesse und Fehlerkorrekturmodelle

Der Differenzenoperator ist, mathematisch be

trachtet, ein „Filter“, mit dem bei nicht-integrier

ten Prozessen niederfrequente Schwingungen ei

ner Zeitreihe eliminiert bzw. abgeschwächt und höherfrequente Schwingungen stärker betont wer

den. Deshalb eignet er sich ja zur „Trendbereini

gung“ ; denn der „Trend“ läßt sich formal als Kom

positum langgezogener Sinusschwingungen auffas

sen, wobei ein „linearer“ Trend als Grenzfall einer Sinusschwingung mit unendlich langer Periode auftritt. Es kann nun durchaus der Fall sein, daß bestimmte soziale Indikatoren, Y und X, in ihren langfristigen Verlaufskomponenten einen struktu

rellen Zusammenhang bilden, yt =f (x{), ihre kurz

fristigen Fluktuationen aber nicht oder nur sehr

28 Es ist zu beachten, daß der empirische Autokorrela

tionskoeffizient die wahre Autokorrelation unterschätzt;

das Problem der Nicht-Stationarität bleibt also im Prinzip bestehen (Nelson/Kang 1984: 79).

schwach kovariieren, Ayt * f(A*,). Das heißt, es ist denkbar, daß man mit Hilfe der Differenzenbil

dung das Problem der Scheinkausalität (Scheinre

gression) vermeidet, dabei aber in die Falle der scheinbaren Nicht-Kausalität gerät. Das Konzept der „Kointegration“ zweier oder mehrerer nicht

stationärer Prozesse bietet, unter bestimmten Vor

aussetzungen, einen Ausweg aus diesem Dilemma.

Die erste Bedingung ist, daß die Zeitreihen, deren Zusammenhang man untersuchen möchte, inte

grierte Prozesse der gleichen Ordnungsstufe d sind, daß sie also jeweils durch d-fache Differen

zenbildung in stationäre Reihen transformiert wer

den können. Reihen, die mit einem unterschiedli

chen Ordnungsgrad integriert sind, können keinen langfristigen linear-strukturellen Zusammenhang bilden.29 Die zweite Bedingung ist, daß es für die gleichermaßen integrierten Prozesse mindestens eine (bei nur zwei Reihen genau eine) Linearkom

bination gibt, die stationär ist. Dies ist nicht selbst

verständlich, denn eine Linearkombination zweier (oder mehrerer) 7(d)-Prozesse ist im allgemeinen wiederum ein 7(d)-Prozeß. Erst wenn beide Bedin

gungen erfüllt sind, spricht man von „kointegrier- ten“ Prozessen.

Eine stationäre Linearkombination nicht-stationä

rer Prozesse ist offensichtlich nur dann auffindbar, wenn die (stochastischen) Trendbewegungen der einzelnen Zeitreihen miteinander „korrespondie

ren“, wenn eine Änderung des lokalen Trends in X mit einer mehr oder weniger rapiden Anpassung des lokalen Trends in Y verbunden ist. Wenn zwei Zeitreihen korrespondierende deterministische Trendverläufe aufweisen, läßt sich die Frage nach ihrem kausalen Zusammenhang empirisch nicht beantworten. Erst die beobachtete Korrespondenz von Trendabweichungen bzw. Trendänderungen in X und Y liefert einen Beleg für einen eventuell be

stehenden kausalen Zusammenhang. Stochasti

sche Trends sind per Definition sich verändernde Trends; ihre Korrespondenz (Kovariation) über mehrere Zeitreihen ist nicht determiniert, sondern empirisch offen; wird sie beobachtet, stützt sie die Hypothese eines kausalen Zusammenhangs; wird sie nicht beobachtet, ist die Kausalhypothese wi-

29 Dies besagt nur, daß sich diejenigen Zeitreihen, für die ein linear-struktureller Zusammenhang spezifiziert wer

den soll, im gleichen Integrationsgrad befinden. D ie Roh

daten können einen unterschiedlichen Integrationsgrad aufweisen oder erst durch eine Transformation in eine DSP-Struktur überführt werden. Zum Beispiel wird der Preisindex häufig in Form der Inflationsrate, also der „dif

ferenzierten“ logarithmierten Werte, als Regressor- variable eingesetzt (siehe unten).

(13)

2 1 4 Zeitschrift für Soziologie, Jg. 26, Heft 3, Juni 1997, S. 202-221

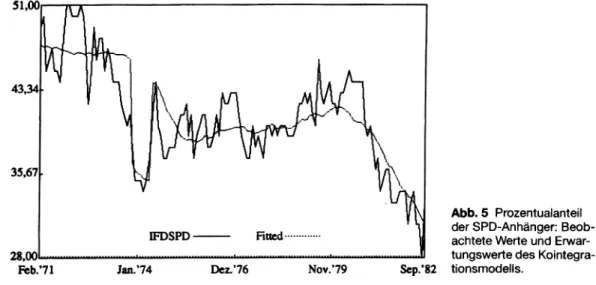
Abb. 5 Prozentualanteil der SPD-Anhänger: Beob

achtete Werte und Erwar

tungswerte des Kointegra- tionsmodells.

derlegt (beides unter der Voraussetzung korrekter Modellspezifikation). Wie im folgenden noch deutlicher werden wird, läßt sich der langfristige strukturelle Zusammenhang als bewegliche Gleichgewichtsbeziehung deuten: Abweichungen vom Gleichgewicht (dargestellt in den Residuen der statischen Regressionsgleichung) führen zu Anpassungsreaktionen im System.

Dieses Konzept soll nun anhand eines negativen und eines positiven Beispiels veranschaulicht und weiter ausgeführt werden. Wir hatten in Abschnitt 4 festgestellt, daß die „allgemeinen wirtschaftli

chen Erwartungen“ (Abb. 3) einen integrierten Prozeß 1. Ordnung darstellen. Mit dem gleichen Instrumentarium läßt sich feststellen, daß die Zeit

reihe der SPD-Präferenzen im gleichen Zeitraum (s. Abb. 5) ebenfalls einen /(l)-Prozeß repräsen

tieren.30

Dieser Befund verdient schon deshalb Aufmerk

samkeit, weil sich aus der Theorie rationaler Er

wartungsbildung ableiten läßt, daß (Partei-)Präfe- renzen einem random walk, genauer einem ARI- MA(0,1,1)-Modell folgen (s. Kirchgässner 1991:

118 mit Literaturhinweisen).31 Diese Thematik

30 D ie Daten wurden vom Zentralarchiv für Empirische Sozialforschung, Köln, zur Verfügung gestellt (Z A Stu- diennr. 0800). D ie ursprüngliche Erhebung erfolgte durch das Institut für Dem oskopie, Allensbach. D ie Daten ge

ben den Prozentanteil derjenigen Befragten an, die „am nächsten Sonntag SPD wählen würden, falls Wahlen statt

fänden.“

31 Modellschätzungen über die gleiche Untersuchungspe

riode (1971-1982) und über eine zweite Subperiode von

möchte ich hier jedoch nicht weiter verfolgen, sondern mich statt dessen der Frage zuwenden, ob die beiden Variablen, die allgemeinen wirtschaftli

chen Erwartungen AWL und die SPD-Präferenz- anteile, „kointegriert“ sind. Im Falle der Kointe- gration liefert die OLS-Regression der statischen Gleichung

SPDt = a + $AWLt + e, (6-1)

konsistente Schätzer (Engle/Granger-Verfah

ren).32 Wenn die beiden Variablen nicht kointe-

1983 bis 1986 führen Kirchgässner (1991: 118 f.) jeweils zum gleichen Befund wie hier. Wird die Modellschätzung jedoch über die gesamte Periode (1971 bis 1986) vorge

nommen, kann die Nullhypothese des RW auf dem 5% -Si

gnifikanzniveau zurückgewiesen werden.

32 Die Konsistenz (genauer: Superkonsistenz) der OLS- Schätzer ist nicht nur an die Bedingung gebunden, daß alle in die Kointegrationsgleichung aufgenommenen Va

riablen den gleichen Integrationsgrad aufweisen; es darf - auch bei mehr als zwei Variablen - nur eine einzige Koin- tegrationsbeziehung vorliegen (Muscatelli/Hurn 1995).

D ie Konsistenz gilt unter dieser Voraussetzung auch bei autokorrelierten Fehlern (Hamilton 1994: 588). Die Schätzer sind aber nicht effizient und in kleinen Stichpro

ben auch nicht erwartungstreu (finite sample bias der Ord

nung 1/n, s. Engle/Granger 1987:262), da die statische Ko

integrationsgleichung die kurzfristige Beziehungsdynamik nicht berücksichtigt; außerdem sind die üblichen f-Tests für die Signifikanz der einzelnen Regressoren nicht an

wendbar (Muscatelli/Hurn 1995: 173). Zu beachten ist auch, daß der Determinationskoeffizient mit zunehmen

der Stichprobengröße gegen 1 tendiert (Hamilton 1994:

589). Das mindert seine Aussagekraft; andererseits gilt, daß in bivariaten Modellen die Verzerrung bei der Para-