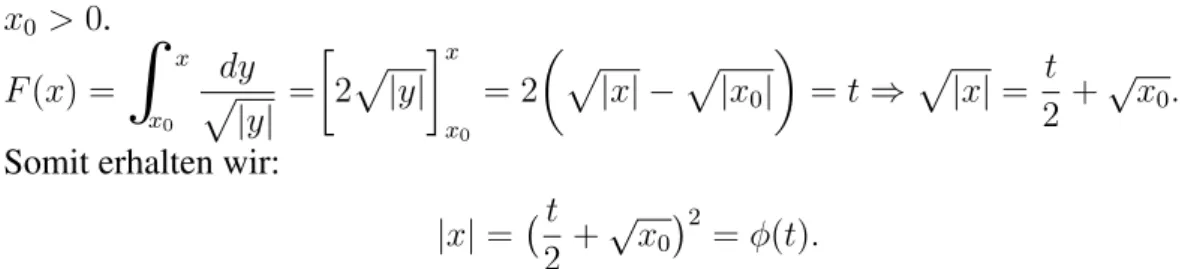Gew ¨ohnliche Differentialgleichungen

Gew ¨ ohnliche

Differentialgleichungen

Inhaltsverzeichnis

1 Einf ¨uhrung in die ODEs 3

1.1 Form von ODEs . . . 3

1.2 Klassifikation von ODEs . . . 3

1.3 Einige Beispiele zu ODEs . . . 4

2 L ¨osungsmethoden f ¨ur ODEs 7 2.1 Trennung der Variablen . . . 7

2.2 Anfangswertproblem einer ODE erster Ordnung . . . 13

2.3 Inhomogene ODEs und Variaion der Konstanten . . . 18

2.3.1 Inhomogene ODEs . . . 18

2.3.2 Variation der Konstanten . . . 19

2.4 Exakte Differentialgleichungen . . . 22

2.5 Koordinatentransformation . . . 27

3 Theorie zu ODEs 33

3.1 Isokline . . . 33

3.2 Lipschitz-Stetigkeit . . . 35

3.3 Existenz und Eindeutigkeit von L¨osungen . . . 39

3.3.1 Banach-Kontraktionsprinzip . . . 39

3.4 Satz von Picard-Lindel¨of . . . 41

3.4.1 Picard-Iteration . . . 43

3.5 Harmonischer Oszillator, Resonanz und Anwendungen . . . 45

3.5.1 Mehr ¨uber Resonanz . . . 49

3.6 Gr¨onwall-Ungleichung . . . 50

4 Systeme von Differentialgleichungen 59 4.1 Das Matrixexponential . . . 59

4.2 Jordansche Normalform . . . 63

4.3 Station¨are Punkte . . . 65

4.4 Lotka-Volterra Gleichungen (R¨auber-Beute-Modell) . . . 70

4.4.1 Erg¨anzung zur Theorie von L¨osungen . . . 74

4.5 Nicht-autonome lineare ODEs . . . 77

5 Vektorfelder 83 5.1 Gradientenvektorfeld . . . 90

5.2 Lyapunov-Funktionen . . . 91

1 Einf ¨ uhrung in die ODEs

Es stellt sich zuerst die Frage was ¨uberhaupt ODEs sind und wozu man ¨uberhaupt lernen sollte, wie man sie l¨ost.

1.1 Form von ODEs

Definition 1. Liegt eine Gleichung folgender Form vor, so handelt es sich um eine ODE:

F(t, x, x⁽¹⁾, ..., x⁽ⁿ⁾) = 0

f¨urx∈C^k(k), t ∈R,k, K¨orper, und den Ableitungen von x

x^(j)= d^(j)x(t)

dt^(j) , j ∈N.

1.2 Klassifikation von ODEs

Leider kann man oft zu ODEs nicht viel sagen, da sie in der Regel ziemlich kompliziert sind und oft besondere Tricks ben¨otigen um gel¨ost zu werden, jedoch gibt es nat¨urlich auch welche, die l¨osbar sind, und um diese zu erkennen f¨uhren wir folgende Klassifika- tionen ein:

Definition 2. Eine ODE der Formx⁽ⁿ⁾(t) +x⁽ⁿ⁻¹⁾(t) +...+x⁽¹⁾(t) = g(t)wird genannt

•Eine ODE n-ter Ordnung, wobei n hier die h¨ochste auftretende Ableitung bezeichnet.

•Homogen, fallsg(t) = 0(ACHTUNG: Eine (nichtlineare) ODE heißt auch homogen, falls sie von folgender Form isty⁰(x) = f(y

))

z.B. nicht mit einem Sinus versehen sind).y⁰(x) =sin(t) +cos(y)ist z.B. nicht linear.

(Vorsicht bei nichtlinearen ODEs kann man den Begriff der Homogenit¨at nicht mitneh- men)

•Autonom, falls die Funktion nicht explizit von der unabh¨angigen Variable abh¨angt.

y⁰(x) = y²+xist z.B. nicht autonom, da x, die unabh¨angige Variable, explizit vorkommt.

•ODE mit konstanten Koeffizienten, falls alle Koeffizienten der gesuchten Funktion nicht variieren.y⁰(x) +a(x)y(x) = 0hat z.B. variierende Koeffizienten wegena(x)y(x).

1.3 Einige Beispiele zu ODEs

Nun haben wir vorerst genug Theorie und wollen uns nun konkreten Beispielen widmen:

•m· d²~x

dt² =F~(~x)→System von ODEs (xist hier ein Vektor imR³), 2. Newton’sches Gesetz

•Radioaktiver Zerfall :N ≥0,dN

dt =−λN

Nun wollen wir uns ein Beispiel genauer anschauen und es analysieren und auch l¨osen : Wir haben folgende ODE gegeben und wollen sie auch l¨osen:

f⁰(t) =

f(t) cos(t)

2

.

Wie wir hier sehen bekommen wir ein Problem, wenn dercos(t) = 0ist, weshalb wir unser Intervall auf(−π

2,π

2)beschr¨anken werden, wobei wir noch f(0) = f₀ als An- fangswert (InitialValue) setzen.

Nun stellt sich die Frage wie wir diese Gleichung l¨osen k¨onnen. Da es eine Differential- gleichung ist, w¨are Integrieren eine Idee jedoch k¨onnen wir in der Form in der wir die Gleichung jetzt haben nicht einfach losintegrieren, da die Variablen alle durcheinander

gemischt sind. Um integrieren zu k¨onnen, m¨ussen wir die Gleichung erstmal umschrei- ben, und das machen wir indem wir durchf(t)²dividieren und so erhalten wir:

f⁰(t)

f²(t) = 1 cos²(t) .

Wir sehen nun dass die Gleichung zum integrieren besser aussieht, da alle f(t) also die Terme die nach f integriert werden auf einer Seite, und die die nach t integriert werden, also in dem Fallcos²(t)auf einer Seite stehen, das heißt wir haben die Variablen separiert.

Wir erhalten nun:

Z

f⁰(t) f²(t) =

Z

1 cos²(t)

⇐⇒ − 1

f(t) = tan(t) +c .

Wir erhalten somit als allgemeine L¨osung f¨ur unsere Differentialgleichung : f(t) = −1

tan(t) +c, und da wir noch unseren IV gegeben hatten, k¨onnen wir das c be- stimmen und erhalten:

f(0) =f₀ ⇐⇒c= −1 f0

.

-4 -2 2 4

-6 -4 -2 2 4 6

Abbildung 1: Plot f¨ur c=0

-4 -2 2 4

152 154 156 158 160 162

Abbildung 2: Plot f¨ur c=50π

2 L ¨ osungsmethoden f ¨ ur ODEs

2.1 Trennung der Variablen

Wir haben unsere vorherige ODE mit der Methode der Trennung der Variablen gel¨ost.

Wir werden uns nun anschauen, wie diese Vorgehensweise Funktioniert, wann sie funk- tioniert, und werden dabei merken dass man sie eigentlich fast nie wieder brauchen wird was die komplexeren Vorgehensweisen der Natur betrifft.

Stellen wir uns zun¨achst die Frage, wie wir folgende Gleichung l¨osen k¨onnen:

y⁰ =f(x)·g(y) .

Wir wollen diese Gleichung nun nachyaufl¨osen und schreiben daher:

dy

dx = f(x)· g(y) es wird hier nun das dx auf die andere Seite durch ”multiplizie- ren”gebracht. (Es sei an dieser Stelle erw¨ahnt, dass das mathematisch alles andere als korrekt ist, denn man m¨usste eigentlich substituieren, aber f¨ur unsere Zwecke reicht das vollkommen aus, da es uns dasselbe ergebnis bringt).

Wir erhalten nun:

dy=f(x)·g(y)dx.

Nun dividieren wir durchg(y)und erhalten:

dy

g(y) =f(x)dx

f¨ur y 6= 0(y = 0ist in diesem Fall eine konstante L¨osung, aber uninteressant). Nun

Integrieren erm¨oglicht und erhalten:

Z

dy g(y) =

Z

f(x)dx.

Sei nun G die Stammfunktion von 1

g und F die Stammfunktion vonf(x). Wir erhalten somit:

G(y) =F(x) +c

und durch Umformen erhalten wir unser gesuchtesy, was so aussieht:

y =G⁻¹(F(x) +c)

mitG⁻¹ als Umkehrfunktion von G. Hier sieht man nun, dass das Prinzip der Trennung der Variablen darin besteht, alle Variablen einer Gattung auf eine Seite zu bringen (z.B.

alle y nach links und alle x nach rechts) um das integrieren zu erm¨oglichen. Es folgen nun weitere Beispiele, damit das Prinzip dieser L¨osungsmethode verinnerlicht wird, da seperable Gleichungen im Gegensatz zu anderen Arten angenehm zu handhaben sind.

•Gegeben sei die Gleichungy⁰ =g(y x).

Man kann versuchen diese Gleichung zu separieren wird dabei aber keine Freunde haben und es auch nicht schaffen. Hier muss eine Variablentransformation durchgef¨uhrt werden um die Gleichung seperabel zu machen. Hierf¨ur sagen wiru= y

x undy(x) = xu(x).

Durch Ableiten und anwenden der Produktregel erhalten wir

y⁰ =x·u⁰+u=g(y x).

Auf diese Weise erhalten wir eine Gleichung der Form:

u⁰ = g(u)−u x

Diese Gleichung ist separabel und durch l¨osen dieser Gleichung und R¨ucksubstitution kann die urspr¨ungliche Gleichung gel¨ost werden.

•Nun ein etwas l¨angeres Beispiel mit Diskussion der gefundenen L¨osungen am ende:

Gegeben sei eine Gew¨ohnliche Differentialgleichung (welcher Art?) folgender Gestalt:

N⁰(t) =κ(1− N(t) Nmax

)N(t), N(0) =N₀

mitN(t)als Anzahl einer Bakterienkultur zum Zeitpunkt t,κ >0als Wachstumsrate, N0 als Bakterienmenge zum Zeitpunkt t = 0 und Nmax als maximale Kapazit¨at f¨ur Bakterien.

Man l¨ose diese ODE und disktuiere das Verhalten vonN(t)f¨urt → ∞.

Wir werden die L¨osung in folgende Schritte gliedern:

1. Schritt : Die Gattung dieser ODE feststellen 2. Schritt : Welche Methode wenden wir an?

3. Schritt : Die Variablen Trennen

4. Schritt : Die Integrale L¨osen (in diesem Fall wird das Werkzeug der Partialbruchzerle- gung ben¨otigt)

5. Schritt : L¨osung formal aufschreiben, alle F¨alle ausschließen und die L¨osungen disku- tieren.

1.) Hierbei handelt es sich um eine Gew¨ohnliche Differentialgleichung erster Ordnung

Auf gehts mit dem separieren:

N⁰(t) =κ(N(t)− N(t)² N_max) Man dividiere durch(N(t)− N(t)²

N_max)und erh¨alt dadurch N⁰(t)

N(t)− N(t)² N_max

! =κ.

Man schreibe die linke Seite um, und integriere beide Seiten. So erh¨alt man:

Z

N⁰(t)dt N(t)· 1− N(t)

N_max

! =

Z

κdt.

Wir k¨onnen die linke Seite etwas umformen und erhalten so:

N_max

Z

sss N⁰(t)dt N(t)· N_max−N(t)

! =

Z

κdt.

4.) Nun muss man die Integrale l¨osen. Die rechte seite sollte kein Problem darstellen, die Linke ben¨otigt jedoch die Partialbruchzerlegung, die wir nun durchf¨uhren werden.

Ziel ist es die linke Seite in folgenden Ausdruck zu bringen:

N⁰(t)

N(t)·(N_max−N(t)) = A

N(t)+ B N(t)−N_max

. Die Rechte Seite besteht aus Termen A und B, welche durch die beiden Nullstellen der linken Seite dividiert werden, denn falls N(t)=0 ist oderN(t) =N_maxist, so wird der

Nenner der linken Seite 0.

Nun bringen wir die rechte Seite auf gemeinsame Nenner und erhalten dadurch:

A·(N(t)−N_max) +B(N(t)) N(t)·(N_max−N(t)) . Durch herausheben und Umformen erhalten wir:

(A+B)(N(t))−A(N_max) N(t)·(N_max−N(t)) .

Durch Koeffizientenvergleich der rechten und linken Seiten sehen wir nun, dass:

A+B = 0und −A(N_max) = 1sein muss und daher folgt daraus:

A=− 1

N_max undB = 1 N_max,

womit wir die Partialbruchzerlegung durchgef¨uhrt haben, welche folgendes Endergebnis liefert:

N⁰(t)

N(t)·(N_max−N(t)) =− 1

N_maxN(t)+ 1

N_max(N(t)−N_max).

Nun k¨onnen wir die linke Seite durch den neuen Ausdruck ersetzen und erhalten dadurch:

Z

− 1

N_maxN(t)+ 1

N_max(N(t)−N_max)dN =

Z

κdt.

Nun k¨onnen wir die linke Seite in zwei Integranden aufspalten und erhalten dadurch:

− 1 N_max

Z

1

N(t) + 1 N_max

Z

1

N(t)−N_max =

Z

κdt

Integrieren wir beide Seiten, so erhalten wir

− 1

N_max log(N(t)) + 1

N_max log((N(t)−N_max)) =κt+c.

Nun ist es nur noch eine Frage des Umformens, wie wir auf unser N(t) kommen.

F¨uhren wir nun die ¨Aquivalenzumformungen durch, so erhalten wir als endg¨ultige L¨osung:

N(t) = e^κt+cN_max 1−e^κt+c

5.) Wir sehen nun, dass f¨urt → ∞auchN(t) → ∞geht, also das Wachstum rapide zunimmt.

Das war es vorerst mit der Methode der Trennung der Variablen. Wir m¨ochten nochmals wiederholen wann und wie man solche Gleichungen durch diese Methode l¨ost.

Zuerst ¨uberpr¨uft man ob diese Gleichung erster Ordnung ¨uberhaupt seperierbar ist.

Ist sie es, so bringt mal alle Variablen auf eine Seite. Hat man dies getan, so integriert man beide Seiten jeweils nach der vorhandenen Variable und formt das Ergebnis auf die gew¨unschte Form um.

2.2 Anfangswertproblem einer ODE erster Ordnung

Wir wollen uns nun Anfangswertproblemen widmen und haben folgendes IVP gegeben:











x⁰(t) =f(x(t)) x(0) =x₀,

=: (+)

Weiters sagen wir, dassf : R → Rstetig ist, undf(x₀)6= 0, da sonstx(t) = x₀ eine L¨osung w¨are, und das nat¨urlich langweilig ist.

Wir nehmen nun(+)und dividieren hier durchf(x(t))und erhalten:

x⁰(t) f(x(t)) = 1.

Nun integrieren wir beiden Seiten und erhalten dadurch:

dy=x⁰(s)ds

Z

0

x⁰(s)

f(x(s))ds =t,

mitF(x) =

R

dy f(y).

Wir wissen, dassF(x)beix≈x₀ monoton ist, und deshalb in dem Bereich invertierbar ist. Hier definieren wir unsφ(t) =F⁻¹(t) = x.

Nun stellt sich uns die Frage, wie langeφ(t)nun existiert. Wir definieren uns(x₁, x₂), als das gr¨oßte Intervall, auf demf >0ist. Weiters definieren wir unsT₁ := lim

x&x1

F(x) undT = lim F(x).

Wir wollen nun 2 F¨alle f¨urT₂unterscheiden:

1.Fall:T₂ =∞= lim

x%x2

R

x0

1

f(y)dy⇒ 1

f ist nicht integrierbar.

2.Fall:T₂ <∞. Dieser Fall spaltet sich nochmals in 2 F¨alle auf:

Fall 2a:x2 =∞ ⇒ lim

t→T₂φ(t) = x2 =∞also nicht fortsetzbar.

Fall 2b: x₂ < ∞ ⇒ lim

t→T₂φ(t) = x₂ < ∞ und f(x₂) = 0. Hier kann man φ(t) fortsetzen, alsoφ(t)≡x₂,t≥T₂, jedoch ist die Fortsetzung hier nicht immer eindeutig.

Nun widmen wir uns wieder ein paar Beispielen dazu:

Beispiel 1:f :R→R, x7→x², x₀ >0.

Wir w¨ahlen uns als Intervall, auf demf(x)monoton ist:(x₁, x₂) = (0,∞), somit erhalten wir:

F(x) =

R

dy f(y) =

R

dy y12 =

− 1 y

x x0

= 1 x₀ − 1

x. Dadurch erhalten wir(T₁, T₂) = (−∞, 1

x0

).

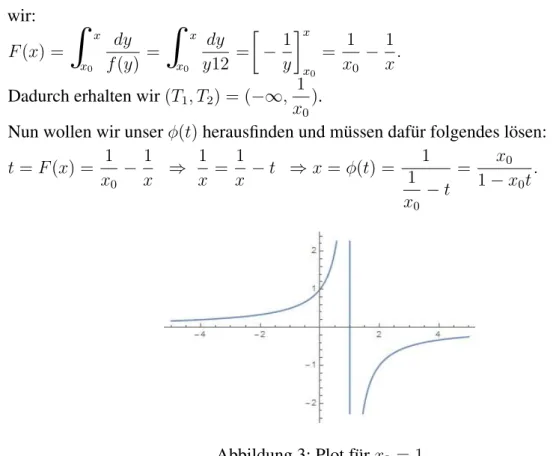
Nun wollen wir unserφ(t)herausfinden und m¨ussen daf¨ur folgendes l¨osen:

t=F(x) = 1 x₀ − 1

x ⇒ 1 x = 1

x −t ⇒x=φ(t) = 1 1 x₀ −t

= x₀ 1−x₀t.

Abbildung 3: Plot f¨urx₀ = 1

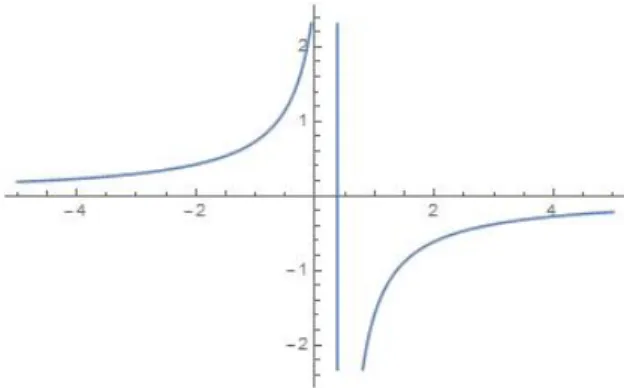
Abbildung 4: Plot f¨urx₀ = 10·π·e

Beispiel 2:f :R→R, x7→p

|x|, mit(x₁, x₂) = (0,∞),(T₁, T₂) = (−2√ x₀,∞) x₀ >0.

F(x) =

R

dy p|y| =

2p

|y|

x x0

= 2

p|x| −p

|x₀|

=t⇒p

|x|= t 2+√

x₀. Somit erhalten wir:

|x|= t 2 +√

x₀2

=φ(t).

Nochmals wie geht man solche Beispiele an?

1.) Man sucht sich das gr¨oßte Intervall(x₁, x₂)in dem die Funktion monoton ist.

2.) Man berechnet sich F(x) mit der FormelF(x) =

R

dy y 3.) Man bestimmt mittelsF(x)das Intervall(T₁, T₂)

4.) Man setztF(x) =tund bestimmt damitx=φ(t).

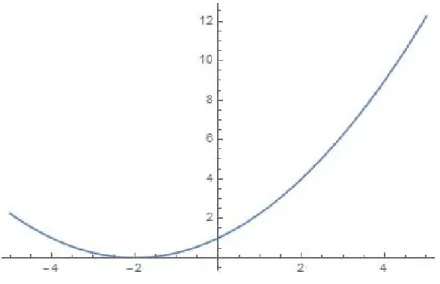
Hier noch zum Abschluss die Plots, welche Parabeln sind:

Abbildung 5: Plot f¨urx₀ = 1

Abbildung 6: Plot f¨urx₀ =e^π

2.3 Inhomogene ODEs und Variaion der Konstanten

2.3.1 Inhomogene ODEs

Wir erinnern uns, dass folgende ODE eine erster Ordnung ist, die zus¨atzlich homogen ist:

x⁰(t) = a(t)x(t), x(0) =x₀

Eine L¨osung von dieser Gleichung erhalten wir durch folgende Formel A(t, t0) =e

Rt t0a(s)ds

. Weiters gelten folgende Eigenschaften:

A(t, t) = 1,A⁰(t,₀) = a(t)A(t, t₀), und die L¨osung unserer ODE lautet:

x(t) = x₀·A(t, t₀).

Nun stell sich die Frage, was wir tun m¨ussen, falls eine inhomogene ODE vorliegt, also eine der Form:

x(t) =a(t)x(t) +g(t), x(0) =x₀.

In diesem Falle haben wir etwas mehr zu tun, denn sowie man Gleichungssysteme l¨ost, indem man zuerst eine spezielle L¨osung sucht und sie zu jener des homogenen Systems addiert, ist das auch bei den L¨osungen von Differentialgleichungen so. Die allgemeine L¨osung f¨ur eine inhomogene ODE ist deshalb:

x(t) =x_hom+x_part.

Man kann auch hier wie bei der homogenen eine L¨osungsformel angeben, welche wie folgt lautet:

x(t) = x₀A(t, t₀) +

R

g(s)A(t, s)ds., wobei der zweite Summand die partikul¨are L¨osung repr¨asentiert.

Nun wollen wir der vollst¨andigkeithalber auch zeigen, dass das wirklich eine L¨osung ist,

und dazu leiten wir x(t) einfach ab:

x⁰(t) =x₀A⁰(t, t₀) +g(t)A(t, t₀) +

Z

t0

g(s)A⁰(t, s)ds

=x₀A(t, t₀) +g(t) + Z t

t0

g(s)a(t)A(t, s)ds

=a(t)

x₀A(t, , t₀) +

Z

t0

g(s)A(t, s)ds

+g(t) = a(t)x(t) +g(t).

Beispiele zum L¨osen von inhomogenen ODEs werden noch viele folgen.

2.3.2 Variation der Konstanten

Wir betrachten folgende ODE:

x⁰(t) = a(t)x+g(t)

Wie schon besprochen werden wir zuerst die homogene Gleichung L¨osen und dann die Variation der Konstanten anwenden um die partikul¨are L¨osung zu bekommen.

x⁰(t) = a(t)xist die homogene Gleichung

⇒ x⁰(t)

x =a(t)⇒log(x) =

Z

t0

a(s)ds+const⇒x(t) =c·e

Rt t0a(s)ds

,

mitc=e^const.

Wir haben zum auffinden der homogenen L¨osung die Trennung der Variablen benutzt und m¨ochten jetzt eine partikul¨are L¨osung durch die Variation der Konstanten finden.

machen, in diesem Fall von t. Wir erhalten somit:

Ansatz:x(t) = c(t)·e

Rt t0a(s)ds

, nun leiten wirx(t)ab, und setzen in unsere urspr¨ungliche ODE ein :

x⁰(t) = c⁰(t)e

Rt t0a(s)ds

+c(t)e

Rt t0a(s)ds

a(t) = g(t) +c(t)e

Rt t0a(s)ds

a(t) Wir sehen nun, dass sich einiges rausk¨urzt und wir erhalten nun:

c⁰(t) =g(t)e⁻

Rt t0a(s)ds

und durch integrieren erhalten wir:

c(t) =

Z

t0

g(u)e⁻

Rt t0a(s)ds

du,

womit das unsere Partikul¨arl¨osung w¨are. Da das etwas viel Theorie ist machen wir nun ein konkretes Beispiel:

Betrachte folgende inhomogene Differentialgleichung erster Ordnung:

x⁰(t) =−x(t)

(auch wenn man hier die partikul¨are L¨osung sofort sieht wenden wir trotzdem die Variation der Konstanten an):

Durch Trennen der Variablen und L¨osen wie gewohnt erhalten wir:

Z v⁰ vdv =

Z

−dt

und wir erhalten als Ergebnis f¨urv(t):

v(t) =c·e^−t,

cals Integrationskonstante.

Nun werden wir dascaus der homogenen L¨osung variieren und erhalten damit:

v(t) = c(t)·e^−t

c⁰(t)·e^−t =v⁰(t) =t−v =t−c·e^−t und wir sehen, dass folgendes gilt:

c⁰(t) = te^−t,

also

c(t) =k+ (t−1)e^t

(l¨osen der DGL liefert das) und wir erhalten als Gesamtergebnis:

v(t) =c(t)e^−t= (k+ (t−1)e^t)e^−t=ke^−t+ (t−1).

Ich m¨ochte an dieser Stelle sagen, dass die Variation der Konstanten ein recht n¨utzliches Werkzeug zum L¨osen von ODEs ist, aber bei den etwas komplizierteren ODEs nicht mehr so oft angewandt wird, da diese Methode allein im Fall von Gleichungen zweiter Ordnung sehr kompliziert wird und es andere, und auch bessere M¨oglichkeiten zum

2.4 Exakte Differentialgleichungen

In diesem Kapitel wollen wir uns nun Gleichungen von folgender Form n¨aher anschauen:

P(x, y) +Q(x, y)· dy dx = 0, oder auch

P(x, y)·dx+Q(x, y)·dy= 0

Gleichungen dieser Form nennt man exakt, falls die sogenannte Integrabilit¨atsbedingung erf¨ullt ist, welche folgendermaßen lautet:

∂P

∂y = ∂Q

∂x.

Satz 1. Ist die Integrabilit¨atsbedingung erf¨ullt, so existiert lokal immer eine Funktion Φ(x, y), sodassP = ∂Φ

∂x undQ= ∂φ

∂y.

Dann definiert die GleichungΦ(x, y) =cf¨ur jedes c implizit eine L¨osung von P(x, y) +Q(x, y)· dy

dx = 0in dem Gebiet(∇Φ = (∂Φ

∂x,∂Φ

∂y)6= 0,Φ(x, y) =c).

Beweis. Man zeige, dassΦ(x, y) = czu L¨osungen f¨uhrt. Wir nehmen eine Funktion x7→y(x), sodassΦ(x, y(x)) = c

=⇒0 = dc dx = d

xΦ(x, y(x)) = ∂Φ

∂x dx dy +∂Φ

∂y + dy

dx =P +Q· dy dx

Wie immer in der Welt der Mathematik ist nicht alles so einfach und es gibt nat¨urlich

auch F¨alle in denen Gleichungen dieser Form nicht exakt sind. Nun stellt sich die Frage nat¨urlich ob man etwas dagegen tun kann, und die Gleichung exakt machen kann. Die Antwort auf diese Frage lautet f¨ur unsere Zwecke ja, denn man kann einen Faktor, genannt Integrierender Faktor, finden, durch den die Gleichung exakt wird. (Im Allgemeinen lautet die Antwort auch ja aber ich m¨ochte hier schon vorweg nehmen, dass die kniffligeren exakten Differentialgleichungen alles andere als angenehme integrierende Faktoren haben f¨ur die man oft ungeheuer viel Zeit braucht um sie herauszufinden, falls

¨uberhaupt m¨oglich). Nun werden wir uns einigen Beispielen widmen, und verschiedene L¨osungsmethoden diskutieren.

Beispiel 1: Gegeben sei folgende ODE:

2x+y²+ 2xyy⁰ = 0.

Man ¨uberpr¨ufe ob die Integrabilit¨atsbedingung erf¨ullt ist, gegebenfalls finde man einen Integrierenden Faktor und l¨ose diese Gleichung. Wie wir feststellen k¨onnen, gilt hier:

∂

∂yQ= 2y= ∂

∂xP = 2y.

Somit sehen wir dass die Gleichung exakt ist und k¨onnen mit dem L¨osen beginnen. Hier m¨ochte ich erw¨ahnen, dass es mehrere Vorgehensweisen gibt. Ich werde beide Methoden verwenden, welche man aber am ende anwendet ist einem selbst ¨uberlassen, bzw. von der Gestalt der Gleichung abh¨angig.

1. Methode (Zweimal Integrieren):

Was wissen wir ¨uber unsere gesuchte FunktionΦ(x, y)? Wir wissen:

Φ(x, y) = Z x

0

Q(s, y)ds=x²+y²+C(y)

Weiters kann man noch schreiben:

Φ(x, y) = Z y

0

P(x, s)ds=y²+D(x)

, wobeiC(y)undD(y)Funktionen abh¨angig von x und y sind.

Nun k¨onnen wir beide Gleichungen vergleichen und bemerken, dass damit Gleichheit herrscht, dassD(x) = x² gelten muss und somit C(y) =ist. Somit erhalten wir f¨ur unsere gesuchte Funktion:

Φ(x, y) =x²+y²+const=c.

Wir definieren uns nunc⁰ =c−constund l¨osen nach y auf (da es in diesem Fall geht) und erhalten:

y= rc⁰

x −x.

Beispiel 2:

Gegeben sei Folgende Differentialgleichung:

xy⁰+ 3x−2y = 0.

Man l¨ose diese Aufgabe wie zuvor.

Uberpr¨ufen wir hier die Integrabilit¨atsbedingung, so m¨ussen wir feststellen, dass sie¨

nicht erf¨ullt ist, da:

∂

∂xP = 16= ∂

∂yQ=−2 gilt.

Was mache wir nun? Wir versuchen einen Integrierenden Faktorµ(x)abh¨angig vonxzu finden. (Er k¨onnte auch von y abh¨angen, ja sogar von x und y wobei letzteres zu einer Partiellen-Differentialgleichung f¨uhren w¨urde).

Ansatz:

µ(x)xy⁰+ (3x−2y)µ(x) = 0

sei exakt. Nun m¨ussen wir folgende Gleichungen l¨osen, umµ(x)zu finden

∂

∂xP⁰ =µ⁰(x)x+µ(x) = ∂

∂yQ⁰ =−2µ(x) , mit Q’ und P’ als das neue P resp. Q.

Wir erhalten nun folgende Differentialgleichung, die wir mit trennung der Variablen l¨osen k¨onnen:

µ⁰(x)x=−3µ(x)

und durch L¨osen dieser ODE erhalten wir:

µ(x) = cx⁻³.

Unsere neue modifizierte Differentialgleichung (die nun exakt sein sollte) sieht nun folgendermaßen aus:

x⁻²y⁰+ 3x⁻²−2yx⁻³ = 0.

Uberpr¨ufen wir nun die Exaktheit dieser ODE erhalten wir:¨

∂

∂xP =−2x⁻³ = ∂

∂yQ=−2x⁻³

und sie ist somit exakt.

Nun k¨onnen wir wie oben zweimal integrieren und erhalten:

Φ(x, y) = Z y

0

P(x, s)ds =x⁻²y+D(x)

und

Φ(x, y) = Z x

0

Q(s, y)ds=−3

x +x⁻²y+C(y).

Wir k¨onnen nun wieder beide Gleichungen vergleichen und bemerkten, dass

D(x) = −3 x

und das endg¨ultige Resultat lautet:

Φ(x, y) =−3

x +x⁻²y =c.

2.5 Koordinatentransformation

Betrachten wir folgende Gleichung :

x⁰(t) = f(x, t), so k¨onnen wir diese Gleichung nicht auf Anhieb l¨osen, sondern m¨ussen eine Koordinatentransformation durchf¨uhren, welche wie folgt aussieht:

F¨ur die unabh¨angige Variable t setzen wirt = τ(s) ⇐⇒ s = σ(t)(durch invertieren) und f¨ur die abh¨angige:

x=ξ(y, t)⇐⇒y =η(x, t)

Wir erhalten nun durch differenzieren:

d

dsy= d

dsη(x(t(s)), t(s)) = ∂η

∂x dx

dt dτ ds + ∂

∂τη=g(y, s).

Nun zu einem etwas konkreteren Beispiel:

x⁰(t) =f(x t)

Wir wissen, dass diese Gleichung homogen ist, da sie diese besondere Form hat und wir m¨ussen nun eine Variablentransformation durchf¨uhren, welche wie folgt aussieht:

y= x t

und wir erhalten:

y⁰(t) = x⁰(t) t − x

t² ⇐⇒t(y⁰(t) +y(t)) = x⁰(t)

Wir erhalten nun als End-Gleichung:

t(y⁰+y) = f(y)⇐⇒y⁰(t) = f(y) t −y

Wie wir sehen ist unsere neue Gleichung nun separabel und wir k¨onnen sie ganz normal durch Trennung der Variablen l¨osen.

Widmen wir uns nun einer speziellen Art von Differenzialgleichung, n¨amlich der Bernoulli-Differentialgleichung.

Wir haben folgende Differenzialgleichung und wollen sie durch eine Transformation l¨osen:

x⁰(t) = f(t)x+g(t)xⁿ

Wir versuchen nun Folgenden Transformationsansatz:

y^β =x,

und

βy^β−1y⁰ =x⁰ und dadurch wird unsere Anfangsgleichung zu:

βy⁰ =f(t)y+g(t)y^β(n−1)+1

Nun gilt es einβzu finden, sodassβ(n−1) + 1 = 0wird, alsoβ = 1 1−n. Somit ergibt als unsere neue, l¨osbare Gleichung:

y⁰(t) = (1−n)(f(t)y+g(t)).

Nun ein Beispiel:

x⁰(t) = tx+ (2 +t²+ 1)x³ Durch transformieren (wie vorher) erhalten wir:

y⁰(t) =−2ty−2(2t²+ 1)

Diese Gleichung k¨onnen wir mit den uns zur Verf¨ugung stehenden Methoden L¨osen. Wir werden zuerst die homogene Gleichung l¨osen, dann eine partikul¨are finden, damit wir durch die Summe der beiden die allgemeine L¨osung bekommen:

Homogene: L¨osey⁰(t) =−2ty, was mittels Trennung der Variablen geschieht, somit erhalten wir:

y⁰

y =−2t =⇒y =e^−t2 ·c

Partikul¨are L¨osung: Benutze den Polynomialen Ansatz: Da auf der rechten Seite ein Polynom Zweiten Grades steht und auf der Linken eine Ableitung werden als Ansatz ein Polynom Dritten Grades nehmen, da dessen Ableitung eines Zweiten Grades ist.

Versuch:

yp =at³+bt2 +ct+d Leite nun ab und setze ein

y_p⁰ = 3at² + 2bt+ct=−2t(at³+bt²+ct+d)−2(2t²+ 1)

Nun k¨onnen wir einen simplen Koeffizientenvergleich durchf¨uhren und sehen, dass wir nun als partikul¨are L¨osung folgendes erhalten:

y_p =−2t

Somit ist die allgemeine L¨osung :

y(t) =c·e^−t2 −2t

Nun m¨ussen wir nur noch r¨uckransformieren und erhalten dadurch:

y^β =x, β = 1

1−n, n= 3 =⇒x= 1

√

c·e^−t2 −2t.

2.6 Bonusinformation zu speziellen ODEs

•Eine ODE heißt vom Typ Bernoulli, falls sie von folgender Gestalt ist:

x⁰(t) =f(t)x+g(t)xⁿ, n6= 0,1.

F¨uhrt man die Transformationy =x¹⁻ⁿdurch, so erh¨alt man die lineare Gleichung

y⁰(t) = (1−n)f(t)y+ (1−n)g(t).

(Istn= 0odern = 1so ist die ODE schon linear).

•Eine ODE heißt vom Typ Riccati, falls sie von folgender Gestalt ist:

x⁰(t) = f(t)x+g(t)x²+h(t).

Hier haben wir es mit einer besonders kniffligen ODE zu tun (zumindest kann sie es werden), denn diese Gleichung kann man nur l¨osen, indem man eine partikul¨are L¨osung x_p(t)kennt. Falls man es schafft eine zu finden (zu erraten) dann kann man folgende Transformation anwenden:

y= 1

x−x_p(t) und erh¨alt folgende lineare Gleichung:

y⁰(t) =−(f(t) + 2x_p(t)g(t))y−g(t).

•Eine ODE heißt vom Typ d’Alembert, falls sie folgende Gestalt hat:

y(x) =xg(y⁰(x)) +f(y⁰(x))

Um eine L¨osung zu dieser ODE zu finden, braucht man eine L¨osunguund erh¨alt mit der Umkehrfunktionu⁻¹eine L¨osung :

y(x) := x·g(u⁻¹(x)) +f(u⁻¹(x))

•Ein Spezialfall der d’Alembert ODE ist die Clairautsche DGL:

y(x) := x·y⁰(x) +f(y⁰(x))

Nichttriviale L¨osungen dieser ODE sind, mitf, cals differenzierbare Funktionen, welche die Gleichungf⁰(x(c)) +x= 0erf¨ullen, die folgende Gleichung :

Triviale L¨osungen sind, f¨ur im Definitionsbereich von f enthaltene c, die Geraden

y(x) :=cx+f(c).

Wie man sieht ben¨otigen viele dieser speziellen ODEs entweder eine partikul¨are L¨osung oder eine besondere Transformation, was diese Gleichungen recht knifflig zu l¨osen macht (falls sie denn ¨uberhaupt eine L¨osung besitzen).

Nun haben wir genug ¨uber die L¨osungsmethoden gesprochen und wollen uns mit dem gefestigten Grundger¨ust mehr der Theorie widmen.

3 Theorie zu ODEs

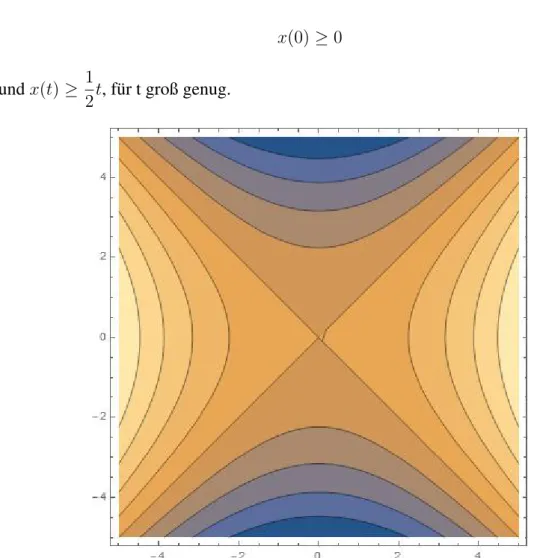
3.1 Isokline

Wir definieren uns nun einige f¨ur dieses Kapitel wichtige Dinge:

Definition 3. x⁺heißt Superl¨osung, fallsx⁰⁺≥f(x⁺) x⁻heißt Subl¨osung, fallsx⁰⁻ ≤f(x⁻)

I(t)heißt Isokline, fallsf(I(t)) =const.

Wir betrachten folgendes Beispiel:

Gegeben sei eine Riccati-ODE, und von ihr seien die Isoklinen zu bestimmen:

x⁰(t) =x²(t)−t² =f(x, t)

Wir l¨osen nunf(I(t)) = 0und erhalten:

I²−t² = 0 ⇐⇒(I−t)·(I +t) = 0

Anhand des folgenden Plots sehen wir die Isoklinen f¨ur dieses konkrete Beispiel. Wir wollen aber uns vorher ¨uberlegen wozu sie ¨uberhaupt gut sind.

Angenommen wir starten in der Mitte beim Ursprung, dann kann unsere L¨osung z.B.

nach rechts unten Gehen und ¨ubertritt dabei eine Isokline. Ist das passiert, so geht sie dann viel st¨arker in Richtung der Isokline bis sie die n¨achste vielleicht trifft, wichtig dabei ist es jedoch zu wissen, dass sie sobald sie eine Isokline ¨ubertreten hat nicht wieder

W¨urden wir uns nunx² −t² = 2w¨ahlen, so istx=√ 2 +t².

Wir sehen nun, dass im oberen Teil des Plots die Steigung≥2ist, und x(t) somit eine Superl¨osung vom Systemξ⁰(t) = 2ist. Die eigentliche L¨osung w¨areξ(t) =c+ 2t. Wir haben hier noch dazux⁰(t)≥2(Superl¨osung), weshalb gilt:

x(t)≥c+ 2t,

x(0)≥0 undx(t)≥ 1

2t, f¨ur t groß genug.

Abbildung 7: Isokline unserer Riccati-ODE

3.2 Lipschitz-Stetigkeit

Nun widmen wir uns einer außerordentlich starken Eigenschaft von Funktionen, n¨amlich der Lipschitz-Stetigkeit:

Definition 4. Eine Funktionf(x, t)heißt Lipschitz-stetig in x, falls eine KonstanteL >0 (Lipschitz-Konstante) existiert, sodass folgende Ungleichung gilt:

kf(x, t)−f(y, t)k< Lkx−yk

f¨ur alle x,y aus dem Definitionsbereich.

Diese Definition setzt allerdings voraus, dassLnicht vontabh¨angig ist, daher brau- chen wir noch die Definition von Gleichm¨aßig Lipschitz.

Definition 5. Eine Funktion f(x,t) heißt gleichm¨aßig Lipschitz-stetig in x, falls es eine KonstanteL≥L_tgibt, sodass∀tgilt:

kf(x, t)−f(y, t)k< Lkx−yk

Da diese Definition ¨außerst wichtig ist, werden wir uns nun ein paar Beispiele dazu anschauen. Lipschitz-stetigkeit ist ¨ubrigens oftmals nur in einer kleinen Umgebung inter- essant. Bevor wir uns aber dem Beispiel widmen, wollen wir uns an einen Satz erinnern, der uns beim herausfinden der Lipschitz-stetigkeit viel helfen wird:

Wir haben eine Funktionf : [a, b]→R, die auf dem abgeschlossenen Intervall [a,b] ste- tig ist, und im offenen Intervall (a,b) sei sie differenzierbar. Gelten diese Voraussetzungen, so gib es mindestens einx₀ ∈(a, b), sodass folgendes gilt:

f⁰(x₀) = f(b)−f(a) b−a

Beispiel 1: Istf(x) = sin(x)Lipschitz-stetig? Ja ist die Antwort und es stellt sich die Frage warum? Zuerst einmal was m¨ussen wir ¨uberhaupt zeigen? Wir m¨ussen zeigen, dass folgendes gilt:

|sin(x)−sin(y)|< L· |x−y|

Erinnern wir uns an den Mittelwertsatz, so erhalten wir:

sin⁰(ξ) = sin(x)−sin(y) x−y

Wir sehen nun, dass wir durch Multiplikation mit dem Nenner unsere gew¨unschte Form erhalten:

|sin(x)−sin(y)|<|sin⁰(ξ)| · |x−y|.

Da wir nun die Form haben, m¨ussen wir nur noch feststellen, ob unsere Lipschitz- Konstante auch wirklich beschr¨ankt ist. In diesem Fall sehen wir es, da die Ableitung vom Sinus der Cosinus ist, und dieser nach oben durch 1 beschr¨ankt ist, ist 1 unsere Lipschitz-Konstante.

Beispiel 2:f(x) =x² auf dem Intervall [0,1]

Hierf¨ur wenden wir wieder den MWS der DR an und erhalten:

|x²−y²|<|2ξ||x−y|.

Hier sehen wir, dass diese Lipschitz-Konstante auf ganzR unbeschr¨ankt ist, weshalb diese Funktion auf ganzRnicht Lipschitz-stetig ist.

Beispiel 3:f(x) =p

|x|

Mit dem MWS der DR erhalten wir:

|√ x−√

y|< 1 2√

ξ|x−y|

Hier sehen wir, dass unsere Funktion auf unserem gegebenen Intervall nicht Lipschitz- stetig ist, aufgrund der Unbeschr¨anktkeit der Lipschitz-Konstante.

Nun, da wir die Lipschitz-stetigkeit hoffentlich verfestigt haben, wollen wir uns einem Satz widmen:

Satz 3. Seif(x, t)Lipschitz in der ersten Variable, und gleichm¨aßig stetig in der zweiten.

Weiters sindx(t), y(t)∈C¹, also (mindestens) einmal stetig differenzierbar, sodass gilt:











x(t₀)≤y(t₀)

x⁰(t)−f(x(t), t)≤y⁰(t)−f(y(t), t)

Dann gilt:

x(t)≤y(t),∀t≥t₀

Diesen Satz werden wir der einfachheithalber nicht beweisen.

Korollar 1. Wenn f(x,t) Lipschitz in der ersten, und gleichm¨aßig in der zweiten Variablen

is, dann hat folgendes IVP h¨ochstens eine L¨osung:











x⁰(t) =f(x, t) x(t₀) =x₀,

Beweis. Sei y(t) eine andere L¨osung von unserem IVP, dann gilt gem¨aß unseres (nicht- bewiesenen) Satzes:

x⁰−f(x(t), t)≤y⁰−f(y(t), t)∀t ≥t₀

und mit dem Satz 3:

x(t)< y(t) ∀t≥t₀, nun tauschen wir und erhalten

y(t)≤x(t) ∀t ≥t₀.

Als Gegenbeispiel h¨aten wir die Wurzelfunktion von vorhin im Bereich von [0,1], wo sie nicht Lipschitz-stetig ist, denn hier h¨atten wir mehrere L¨osungen, n¨amlich:

x(t) = 0 ∀t,

x(t) = 1

4(t−t₀)², ∀t≥t₀ x(t) =−1

4(t−t₁)², ∀t≤t₁.

Einschub 1. Wir erinnnern uns, dass die Mengen von L¨osunungen von ODEs h¨aufig einen Vektorraum bilden, und immer, falls die Gleichungen linear und homogen sind.

Haben wir eine ODE gegeben und sindx(ξ)undx(ζ), so istc·x(ξ) +d·x(ζ)wieder eine L¨osung der ODE.

3.3 Existenz und Eindeutigkeit von L ¨ osungen

3.3.1 Banach-Kontraktionsprinzip

Definition 6. Ein Banachraum X ist ein vollst¨andiger, normierter Vektorraum.

Linearit¨at: F¨urx, y ∈X,α, β ∈Rgilt :αx+βy ∈X.

Norm:k·k:X →Rhat folgende Eigenschaften:

•Positive Definitheit :kxk ≥0undkxk= 0⇐⇒x= 0

•Homogenit¨at:kαxk=|α|kxk, ∀α∈R, x∈X

•Dreiecksungleichung:kx+yk ≤ kxk+kyk

Definition 7. Eine Folge(x_n)n∈Nheißt Cauchy-Folge, falls gilt:

n,m→∞lim kx_n−x_mk= 0.

X heißt vollst¨andig, falls jede Cauchy-Folge in X Konvergiert. Ein Gegenbeispiel hierf¨ur ist der K¨orper der rationalen ZahlenQ, da man sich hier z.B. eine Folge konstru- ieren kann, die gegen√

2konvergiert, aber√

2liegt nicht inQ Banachr¨aume sind z.B.RoderRⁿ.

F¨ur unsere weiteren Beobachtungen wird aber der folgende Banachraum eine wichtige Rolle spielen(dass das ein Banachraum ist werden wir sp¨ater zeigen):

Satz 4. Banachscher Fixpunktsatz

Sei(X,k·k)ein Banachraum undK :X →Xeine Kontraktion, d.h.∃ρ∈(0,1), sodass gilt:

∀x, y ∈Xgilt

kK(x)−K(y)k ≤ρkx−yk

Dann hat K einen eindeutigen Fixpunktx₀ =K(x₀).

Beweis. Sei K : X ∈ X Kontraktion mit Kontraktionsfaktor ρ < 1. Sei weiters R= kKv₀k

1−ρ f¨ur irgendeinv₀ ∈X.

Dann ist die KugelB_R(v₀) = {v ∈X :kv−v₀k ≤R}invariant.

Seiv ∈B_r, dann gilt

kKvk ≤ kKv−Kv₀k+kKv₀k ≤ρkv−v₀k+kKv₀k ≤ρR+kKv₀k ≤R.

Jetzt konstruieren wir uns eine Folgev₀, v₁ =K(v₀), v₂ =K(v₁),· · ·. Diese Folge ist Cauchy, denn

kv_n−v_m|=kK^n−mv_m−v_mk=kK^n−mK^mv₀−K^mv₀k=kK^m(K^n−mv₀)−K^mv₀k ≤

≤ρ^mkK^n−mv₀−v₀k ≤ρ^mR →0, f¨ur m→ ∞.

Fixpunkt existiert: X ist vollst¨andig, alsoVn→V ink·k(alsokVn−Vk →0, f¨urn→

∞)

v =Kv, denn

v = lim

n→∞vn= lim

n→∞Kⁿv0 =K( lim

n→∞Kⁿ⁻¹v0) = K(v) Fixpunkt ist eindeutig:

Seien v und w beide Fixpunkte, dann

kv −wk=kKv−Kwk ≤ρkv−wk,

was nur gelten kann, fallskv−wk= 0, alsov =w.

3.4 Satz von Picard-Lindel ¨ of

Satz 5. Satz von Peano:

SeiΩ⊆R×R^N, seiF : Ω→R^N stetig. Wir betrachten das Anfangswertproblem oder auch Cauchyproblem genannt :

dy

dx =F(x, y),y(x0) =y0., mit

(x₀, y₀) ∈ Ωund y ∈ R^N.So existiert ein IntervallI ⊆ Rmitx₀ ∈ I und mindestens eine L¨osungI 3x→y(x)∈R^N von unserem IVP.

Nun widmen wir uns dem zentralen Satz dieses Kapitels, n¨amlich dem Satz von Picard-Lindel¨of.

Satz 6. Satz von Picard-Lindel¨of

Sei f : U ×[0,1]→ RⁿLipschitz in der ersten und gleichm¨aßig stetig in der zweiten Variablen, so hat folgendes IVP eine eindeutige L¨osung:





x⁰(t) =f(x, t)

Nun wollen wir uns unserem Banachraum-Kandidaten von vorhin widmen.

X =C([0,1],R) = {f : [0,1]→R, f stetig}

mit der Norm

kfk∞ = sup

x∈[0,1]

|f(x)|.

Wir m¨ussen nun zeigen, dass in diesem Raum jede Cauchy-Folge konvergiert.

Seif_neine Cauchyfolge in X.

1.)fnist beschr¨ankt, denn

kf_n−f_mk →0, f¨urn, m→ ∞ ∃m∀n≥mkf_n−f_mk∞ <1

f_mist stetig, also beschr¨ankt auf[0,1], daher

|f_n(x)| ≤ |f_n(x)−f_m(x)|+|f_m(x)|<1 +kf_mk∞.

2.) Finde den Grenzwert

W¨ahlex∈[0,1], dann ist(fn(x))n∈Neine beschr¨ankte Folge (sogar Cauchy) inR, also existiert der punktweise Grenzwert, den wirf(x)nennen.

3.) istf ∈X, also istf stetig?

W¨ahle >0beliebig. Weil(f_n(x))n∈NCauchy ist, gibt esm ∈N, sodass gilt:

∀n≥m:kf_n−f_mk∞<

3

f_mist stetig auf[0,1], also auch gleichm¨aßig stetig, sodass gilt:

∃δ >0, sodass∀x, y ∈[0,1] :|x−y|< δ,

also

|f_n(x)−f_n(y)|<

3 Schlussfolgerung: f¨urx, y ∈[0,1],|x−y|< δ:

|f(x)−f(y)| ≤ |f(x)−fm(x)|+|fm(x)−fm(y)|+|fm(y)−f(y)| ≤

≤ lim

n→∞|fn(x)−fm(x)|+|fm(x)−fm(y)|+ lim

n→∞|fm(y)−fn(y)| ≤

≤ lim

n→∞

3+

3+ lim

n→∞

3 =.

(Bei der Ersten Ungleichung haben wir 2x die Dreiecksungleichung angewandt)

3.4.1 Picard-Iteration

Wir haben U als offene Umgebung des Anfangswertesx₀und sagen:

x₀(t) =x₀

x₁(t) = x₀+ Z t

0

f(x₀(s), s)ds

x₂(t) = x₀+ Z t

0

f(x₁(s), s)ds Allgemein:

Z t

Sei nunK :X →Xeine Kontraktion, dann gilt:

x∞ =K(x^(t)_∞)

mit dem Grenzwert

x∞(t) =x1(t) = x0+ Z t

0

f(x∞(s), s)ds.

Annahme: Fixpunkt von K l¨ost unser IVP (Anfang des Kapitels):

Seiδ >0beliebig,

M := sup

x∈U

sup

t∈[0,1]

f(x, t)<∞, L sei die Lipschitz-Konstante vonf < ∞,

T0 = min{1, δ M, ρ

L}>0undY :=Bδ(x0)⊂X.

1.)K(Y)⊂Y, denn f¨urx(t)∈Y gilt:

kK(x)−x₀k∞ =kx₀+ Z t

0

f(x(s), s)ds−x₀k∞ =

= sup

t∈[0,T₀]

|x₀+ Z t

0

f(x(s), s)ds−x₀| ≤ sup

t∈[0,T₀]

Z t 0

|f(x(s), s)ds| ≤

≤ sup

t∈[0,T₀]

Z t 0

M ds= sup

t

tM =T₀M ≤δ.

2.)

kK(x(s))−K(y(s))k∞ ≤δkx(s)−y(s)k∞∀x, y ∈Y.

kK(x)−K(y)k∞= sup

t∈[0,T0]

|x₀+ Z t

0

f(x(s), s)ds−(x₀+ Z t

0

f(y(s), s)ds)| ≤

≤ sup

t∈[0,T0]

Z t 0

|f(x(s), s)−f(y(s), s)|ds≤ sup

t∈[0,T0]

Z t 0

L|x(s)−y(s)|ds≤

≤L sup

t∈[0,T₀]

Z t 0

sup

u∈[0,T₀]

x(u)−y(u)ds =Lkx−yk sup

t∈,[0,T₀]

·t =

=L·T₀kx−yk_∞≤δkx−yk_∞.

(Notiz hier haben wir die Lipschitz-Stetigkeit verwendet und im Letzten Integral gilt Z t

0

sup

u∈[0,T0]

x(u)−y(u)ds=kx−yk∞.)

3.5 Harmonischer Oszillator, Resonanz und Anwendungen

Wir m¨ochten uns folgendem physikalischen Beispiel aus der Elektrizit¨atslehre widmen::

Wir haben folgende ODE gegeben und m¨ochten sie l¨osen:

I¨+R L

I˙+ 1

LCI = 1

L ·V_Quelle =Acos(ωt)(Wir w¨ahlen das).

Wie l¨osen wir diese Gleichung? Nun wir werden wie schon besprochen zuerst die homogene Gleichung l¨osen, dann eine partikul¨are L¨osung finden und deren Summe ist dann unsere allgemeine L¨osung.

Homogene Gleichung: Wir wollen folgendes L¨osen:

Wir sehen hier dass wir eine ODE haben, dessen Form nach dem Exponentialansatz riecht.

Wir werden daher das charakteristische Polynom l¨osen m¨ussen, welches folgendermaßen aussieht:

λ²+R

Lλ+ 1 CL = 0 (Dies ist im Prinzip unsere Anfangsgleichung nur mit

I¨=λ²,I˙=λ, I = 1)

Wir k¨onnen diese Gleichung mit der kleinen L¨osungsformel l¨osen und erhalten dadurch:

λ_1,2 =

−R L ±

r R L

2

− 4 CL

2 = −R

2L ±i· r 1

CL − R 2L

2

Wir setzen beim Imagin¨arteil (der Wurzel)ω ≈ω⁰,−R

2L = ∆, und erhalten als homogene L¨osung:

Ihom(t) =A1e^∆te^iω0t+A2e^∆te^−iω0t =

=e^∆t(b₁cos(ω⁰) +b₂sin(ω⁰t)).

Nun widmen wir uns der inhomogenen L¨osung (vorerst f¨ur kleines R). Wir sagen:

1

LCI_p(t) = (c₁cos(ωt) +c₂sin(ωt)) 1 LC R

L

I˙p(t) = (−c1ωsin(ωt) +c2ωcos(ωt))R L I¨p(t) = −c1ω²cos(ωt)−c2ω²sin(ωt).

Nun m¨ussen wir alles addieren und Acos(ω)gleichsetzen, um die Form unserer An- fangsgleichung zu erhalten. Wir erhalten somit:

cos(ωt)(c₁( 1

LC −ω²) + c₂R

L ) + sin(ωt)(c₂( 1

LC −ω²)− c₁R

L ) = Acos(ωt).

Wir k¨onnen nun durch umformenc₂ erhalten und haben somit unsere partikul¨are L¨osung:

=⇒c2 = AL

R , Ipart(t) = AL

R sin(ωt).

Nebenbemerkung: Falls R=0 ist w¨urde der Ansatz f¨ur die inhomogene Gleichung so aussehen:

I_p(t) =c₁tcos(ωt) +c₂tsin(ωt).

Wir wollen uns nun f¨ur die Mechanik eine etwas allgemeinere Gleichung ansehen:

¨

x+rx˙ +ω²x=Acos(αt),

wobei hier r allgemein den Widerstand/Reibungsterm beschreibt (r = R

L), das ω² entspricht bei uns dem 1

LC undAcos(αt)ist eine externe Kraft. Anwendungsbeispiele hierf¨ur w¨are das Federpendel in der Mechanik oder eben wie vorher schon betrachtet in der Elektrizit¨atslehre.

Kurz zum Federpendel: Wir haben einen Winkelϕ, eine Massem, die Beschleunigung a und die Fallbeschleunigung g gegeben und erhalten zusammen mit dem zweiten Newtonschen Axiom folgende Gleichung:

mit der Positionx=ϕl. Somit sieht unsere Gleichung folgendermaßen aus:

¨ ϕ+ g

lsin(ϕ) = 0.

Widmen wir uns nun wieder der allgemeineren Gleichung von vorhin und versuchen sie zu l¨osen.

Wir l¨osen wie vorhin zuerst die homogene Gleichung:

¨

x+rx˙ +ω²x= 0

Wir l¨osen nun wieder das charakteristische Polynom:

λ²+rλ+ω² = 0 =⇒λ =−r 2 ±

rr²

4 −ω² = −r 2 ±i

r

w²− r 2

2

wobei wir wenn wir die Diskriminanteω⁰ nennen folgende Gleichung mit den folgenden L¨osungen erhalten:

λ_1,2 = −r 2 ±iω⁰ x_hom(t) =a₁e^λ1t+b₁e^λ2t=e⁻

r

2^t(acos(ω⁰t) +bsin(ω⁰t)),

wobei hiercos(ω⁰t)die Eigenfrequenz des homogenes Systems bezeichnet.

Nun widmen wir uns der L¨osung des inhomogenen Systems:

Wir w¨ahlen folgenden Ansatz:

x_p(t) = (ccos(α) +dsin(αt))

˙

x_p(t) = (−cαsin(αt) +dαcos(αt))r

¨

x_p(t) = −cα²cos(αt)−dα²sin(αt).

Nun addieren wir alle Gleichungen und erhalten:

c(ω²−α²)cos(αt) +d(ω²−α²)sin(αt)−crαsin(αt) +rdαcos(αt) = Acos(αt).

Nun k¨onnen wir diese Gleichung etwas rearrangieren und erhalten:

c(ω²−α²) +rdα=A=⇒ d(ω²−α²)

rα +drα=A=⇒d= A (ω²−α²)²

rα +rα

d(ω²−α²)−crα= 0 =⇒c= d(ω²−α²)

rα =⇒c= A(ω²−α²) (ω²−α²)²+ (rα)². Resonanz tritt hier auf, fallsω²−α² r1.

3.5.1 Mehr ¨uber Resonanz Wir betrachten folgende Gleichung:

¨

x+ω²x=Acos(ωt).

Der unterschied hier ist, dass wir keine Reibung haben, und das rechte Glied sogar eine L¨osung des homogenen Systems ist:

x_hom(t) =acos(ωt) +bsin(ωt).

F¨ur die inhomogene Gleichung w¨ahlen wir den folgenden Ansatz:

xp(t) = ctsin(ωt)

˙

x_p(t) = csinω(t) +cωtcos(ωt)

¨

xp(t) = 2cωcos(ωt)−cω²tsin(ωt) Nun addieren wir wieder die 3 Gleichungen und erhalten:

=⇒Acos(ωt) = 2cωcos(ωt)

und wir k¨onnen damit folgende allgemeine L¨osung finden (Summe der L¨osung des homogenen plus der partikul¨aren L¨osung):

x(t) = A

2ωtsin(ωt) +acos(ωt) +bsin(ωt).

3.6 Gr ¨ onwall-Ungleichung

Wir erinnern uns an den Satz von Picard-Lindel¨of, also haben wir eine Funktionf(x, t) gegeben, mit x Lipschitz inx ∈U ⊂Rⁿund gleichm¨aßig stetig in t, so hat folgendes Anfangswertproblem genau eine L¨osung:











x⁰(t) =f(x, t) x(0) =x₀, Genauer:

Gelten die obigen Voraussetzungen (Lipschitz in 1., gleichm¨aßig in zweiter Variablen),

dann existiertT₀ ∈[0,1]f¨ur das es genau eine L¨osungϕ(t)von dem Anfangswertpro- blem gibt. Die Existenz gilt f¨urt∈[t₀, t₀+T₀].

Zus¨atzlich zu unserem IVP betrachten wir noch folgendes IVP :











y⁰(t) =g(y, t) y(t₀) = y₀,

Betrachten wir nun folgendes Beispiel:

f(x, t) = g(x)≡λx, t₀ = 0,

so haben wir:

˙

x=λx, x(0) =x₀y˙ =λy, y(0) =y₀.

Wir k¨onnen die Gleichungen mit unseren Standardmethoden l¨osen und erhalten:

x(t) = x₀e^λt, y(t) =y₀e^λt

und wir wissen, dass:

|x(t)−y(t)|=|x₀−y₀|e^λt.

Satz 7. Seienf, g ∈C(U×[t₀, t₀+ 1],Rⁿ), f Lipschitz inx∈U, in t gleichm¨aßig, mit L= supx6=y,t∈[0,1]

|f(x, t)−f(y, t)|

x−y ≥0als Lipschitz-konstante und M = supx6=y,t∈[0,1]|f(x, t)−g(x, t)| ≤ ∞.

Seien weiters x(t) und y(t) L¨osungen von unseren beiden IVP, die Auf[0, T0]existieren, dann gilt:

|x(t)−y(t)| ≤ |x₀−y₀|e^Lt+M

L (e^Lt−1).

Um diesen Satz zu beweisen m¨ussen wir erst die Gr¨onwall-Ungleichung und deren Spezialf¨alle bearbeiten.

Seienβ ≥0, α(t)∈Rund weiters nehmen wir an:

ψ(t)≤α(t) + Z t

0

β(s)ψ(s)ds

Wir definieren uns:

ϕ(t) =e^{−R0t0β(s)ds},

dann f¨uhren wir folgende Schritte durch:

d dt(ϕ(t)

Z t 0

β(s)ψ(s)ds) =

=ϕ(t) Z t

0

β(s)ψ(s) +ϕ(t)β(t)ψ(t)ds=

=−β(t)e^{−R0tβ(s)ds} Z t

0

β(s)ψ(s) +ϕ(t)β(t)ψ(t) =

=β(t)ϕ(t)(ψ(t)− Z t

0

β(s)ψ(s)ds)≤β(t)ϕ(t)α(t).

Nun integrieren wir beide Seiten und erhalten:

ϕ(t) Z t

0

β(s)ψ(s)ds≤ Z t

0

β(s)α(s)ϕ(s)ds,

also gilt:

Z t 0

β(s)ψ(s)ds ≤ 1 ϕ()

Z t 0

β(s)α(s)ϕ(s)ds.

Und mit unserer Gr¨onwall Ungleichung erhalten wir:

ψ(t)≤α(t) + Z t

0

β(s)ψ(s)ds≤α(t) + Z t

0

β(s)α(s)e^Rstβ(u)du.

F¨ur unsere Berechnungen ist folgendes Resultat noch wichtig:

ϕ(s)

ϕ(t) = e^{−R0sβ(u)du} e^{−R0tβ(u)du} =e⁻

Rs

0β(u)du−(−Rt 0β(u)du)

=e

Rtβ(u)du

s .

Nun widmen wir uns den beiden Spezialf¨allen der Gr¨onwall-Ungleichung 1. Spezialfall:

α(s)≤α(t)∀s≤t.

Sind diese Bedingungen erf¨ullt, so ergibt Gr¨onwall:

ψ(t)≤α(t) + Z t

0

β(s)α(s)e^Rstβ(u)duds≤

≤α(t)(1 + Z t

0

β(s)(e^Rstβ(u)du)ds =

=α(t)(1− Z t

0

d

dse^Rstβ(u)duds) =

=α(t)(1−1 +e^R0tβ(u)du) Mit diesen Resultaten erhalten wir:

ψ(t)≤α(t)e

Rt 0β(u)du

.

Erkl¨arungen der wichtigen Schritte: Die erste Ungleichung gilt, daα(s)≤α(t),

d

dse^Rstβ(u)du=e^Rstβ(u)du(−β(s)),

das ¨entsteht dadurch, dass wir nach der unteren Integrationsgrenze differenzieren.

Seienγ, α∈R, β ≥0const Seiψ(t)≤Rt

0(βψ(s) +γ)ds:=(+) So gilt:

ψ(t)≤αe^βt+ γ

β(e^βt −1), mit dem Grenzfall

β = 0, ψ(t)≤α+γ(t),

also:

β→0lim γ

β(e^βt−1)

wodurch wir mit der Regen von L’Hˆopital folgendes erhalten:

β→0lim γ

1t=γt.

Der Beweis folgt, indem man

ψ(t)⁰ =ψ(t) + γ β

setzt, denn dann wird(+)zu :

ψ(t)⁰−β

γ ≤α+ Z t

0

β(ψ(s)⁰− γ

β) +γds

=⇒ψ(t)⁰ ≤(α+ γ β) +

Z t 0

βψ(s)⁰ds.

Nun kann man Spezialfall 1 anwenden, also:

ψ⁰(t)≤(α+ γ

β)e^R0tβ(u)du

ψ(t) + γ

β ≤α+ γ

βe^R0tβ(u)du

=⇒ψ(t)≤αe^βt+ γ

β(e^βt−1).

Wir bemerken nun, dass die Ungleichung aus Satz 7 so aussieht wie der 2. Spezialfall der Gr¨onwall Ungleichung.

Fassen wir nun zusammen:

Lemma 1. Gr¨onwalls Lemma Seiβ ≥0, α(t)∈R.

Falls

ψ(t)≤α(t) + Z t

0

β(s)ψ(s)ds,

dann gilt auch:

ψ(t)≤α(t) + Z t

0

α(s)β(s)e^Rstβ(u)duds.

Spezialfall 1: Falls zus¨atzlich

α(s)≤α(t)∀s ≤t

gilt, dann auch:

ψ(t)≤α(t)e^R0tβ(s)ds

Spezialfall 2: Falls

β ≥0, α, γ ∈Rconst

und

ψ(t)≤α+ Z t

0

(βψ(s) +γ)ds

gilt, dann auch :

ψ(t)≤αe^βt+ γ

β(e^βt1).

Sollte zus¨atzlichβ = 0sein, dann gilt sogar:

ψ(t)≤α+γt.

Nun stellt sich die Frage wozu man ein solches kompliziertes Konstrukt braucht. Diese Ungleichung wird zur Stetigkeit von L¨osungen von Anfangswertproblemen ben¨otigt. Als Beispiel werden wir die Ungleichung aus Beispiel 7 beweisen:

Beweis. Wir haben :

|x(t)−y(t)| ≤ |x₀−y₀|+ Z t

0

(f(x(s), s)−g(y(s), s))ds ≤