e , sin x, √ a a ( x − x ) X 1+ x + x + ... + x + ... = x =11 x X | x | < 1 . x P x ∈ . f x ∈ ( − ( x 1 , 6 =1) 1) , 9.3Taylor-Reihen x, − ln x x f ( x )

9.3 Taylor-Reihen 361

9.3 Taylor-Reihen

Wir kommen nun zum zentralen Thema dieses Kapitels: die Taylor-Reihen.

Die Aussage des Taylorschen Satzes ist, dass sich fast jede elementare Funktion in der Umgebung eines Punktesx₀ durch Polynome beliebig genau ann¨ahern l¨asst. Es zeigt sich sogar, dass diese Funktionen sich durch eine Potenzreihe der Form

∞

X

n=0

a_n (x−x₀)ⁿ

darstellen lassen. Neben der Bestimmung der Koeffizientenan werden wir In- formation dar¨uber gewinnen, welcher Fehler maximal auftritt, wenn diese Reihe nach endlich vielen Summationsgliedern abgebrochen wird. Damit erhalten wir zum einen eine Methode, die elementaren Funktionen

e^x,sinx,√

x,lnx usw.

mit beliebiger Genauigkeit zu berechnen, zum anderen N¨aherungsformeln f¨ur diese Funktionen.

Beispiel 9.25 (Einf¨uhrung): Nach Beispiel 9.19 gilt f¨ur die geometrische Potenzreihe

1 +x+x²+. . .+xⁿ+. . .=

∞

X

n=0

xⁿ= 1 1−x f¨ur |x| < 1. D.h. die Potenzreihe P∞

n= 0xⁿ stimmt mit der Funktion _1−x¹ f¨ur allex∈(−1,1) ¨uberein. Außerhalb dieses offenen Intervalls ist zwar _1−x¹ noch definiert(x6= 1),aber nicht mehr die Potenzreihe. Wir leiten eine Formel heuristisch her, die es uns erlaubt, f¨ur elementare Funktionen die zugeh¨orige Potenzreihe aufzustellen.

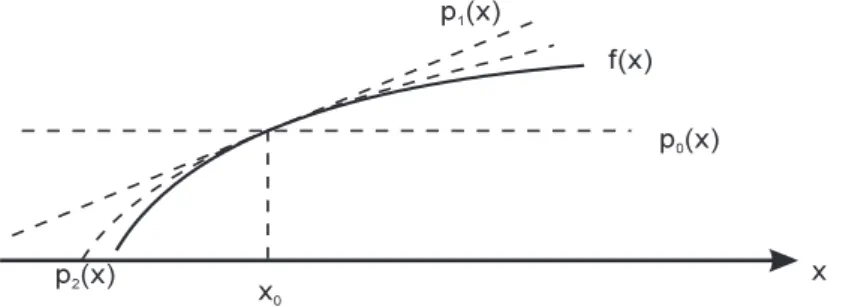
Herleitung der Taylor-Polynome. Gegeben sei eine Funktion f(x), siehe Abb. 9.3. Gesucht ist eine N¨aherung der Funktion in der Umgebung des Punk- tesx₀∈ID.Die Funktionf sei in dieser Umgebung mehrmals differenzierbar.

Abb. 9.3.Funktionfund N¨aherungen in der Umgebung vonx0

362 9. Funktionenreihen

(0.) Die ”nullte” N¨aherungp0an die Funktion erh¨alt man, wenn die konstante Funktion

p₀(x) =f(x₀)

gew¨ahlt wird. Die Funktion p0 hat mit f nur den Funktionswert an der Stellex0 gemeinsam.

(1.) Die lineare N¨aherungp1an die Funktion erh¨alt man, wenn man die Tan- gente inx0 w¨ahlt:

p₁(x) =f(x₀) +f⁰(x₀) (x−x₀).

Die Tangente hat mit der Funktion sowohl den Funktionswert, als auch die Ableitung an der Stellex0 gemeinsam.

(2.) Gesucht ist eine quadratische Funktion p2, die im Punkte x0 zus¨atzlich die gleiche Kr¨ummung wief aufweist:

Ansatz: p₂(x) =f(x₀) +f⁰(x₀) (x−x₀) +c(x−x₀)². Bedingung: p⁰⁰₂(x0)=^! f⁰⁰(x0).

Wegen p⁰⁰₂(x) = 1·2·c,folgtp⁰⁰₂(x0) = 1·2·c=f⁰⁰(x0)

⇒ c= 1

2!f⁰⁰(x₀)

⇒ p2(x) =f(x0) +f⁰(x0) (x−x0) +f⁰⁰(x₀)

2! (x−x0)².

(3.) Gesucht ist die kubische Funktionp₃, die im Punktex₀ zus¨atzlichdie 3.

Ableitung mitf gemeinsam hat:

Ansatz:p3(x) =f(x0)+f⁰(x0) (x−x0)+_2!¹f⁰⁰(x0) (x−x0)²+d(x−x0)³. Bedingung: p⁰⁰⁰₃ (x0)=^! f⁰⁰⁰(x0).

Wegen p⁰⁰⁰₃ (x0) = 1·2·3·d=^! f⁰⁰⁰(x0)

⇒d= 1

3!f⁰⁰⁰(x0)

⇒ p3(x) =f(x0) +f⁰(x0) (x−x0) +_2!¹ f⁰⁰(x0) (x−x0)² +_3!¹ f⁰⁰⁰(x0) (x−x0)³.

9.3 Taylor-Reihen 363 ...

(n.) Eine bessere Approximation an die Funktion f in einer Umgebung des Punktesx0gewinnt man, indem jeweils Terme der Form

1

n!f⁽ⁿ⁾(x0) (x−x0)ⁿ

hinzugenommen werden, so dass das n-te N¨aherungspolynom (das Taylor- Polynom vom Graden) gegeben ist durch

pn(x) = f(x0) +f⁰(x0) (x−x0) +. . .+ 1

n!f⁽ⁿ⁾(x0) (x−x0)ⁿ

=

n

X

i=0

1

i!f⁽ⁱ⁾(x0) (x−x0)ⁱ.

Visualisierung: Zur Veranschaulichung der Konvergenz der Taylor- Polynome pn an die Funktion f w¨ahlen wir eine Animation f¨ur die Funktion f(x) =

q

6−(x−2.5)² am Entwicklungspunkt x₀ = 1. Dazu be- stimmen wir die ersten 10 Taylor-Polynome.

Durch die Animation erkennt man deutlich, dass mit wachsendem Grad des Taylor-Polynoms der Bereich sich vergr¨oßert, in dem Funktion und Taylor- Polynom graphisch ¨ubereinstimmen. F¨ur N = 10l¨asst sich im Bereich0.5≤ x ≤ 1.7 graphisch kein Unterschied zwischen der Funktion f und dem N¨a- herungspolynom p10 feststellen. Es stellt sich somit die Frage, wie groß die Abweichung der N¨aherungsfunktion p_n(x) zur Funktion f in der Umgebung vonx0ist. Aufschluss dar¨uber gibt der folgende Satz.

364 9. Funktionenreihen

Satz von Taylor.Gegeben sei eine inx0∈ID (m+ 1)-mal stetig dif- ferenzierbare Funktionf. Dann gilt dieTaylorsche Formel

f(x) =f(x₀) +f⁰(x₀) (x−x₀) +. . .+ 1

m!f^(m)(x₀) (x−x₀)^m+R_m(x) mit dem Restglied

Rm(x) = 1

(m+ 1)!f^(m+1)(ξ) (x−x0)^m+1 (x∈ID) undξ einem nicht n¨aher bekannten Wert, der zwischenxundx₀ liegt.

Der Satz von Taylor (1685 - 1731) spezifiziert die Zwischenstelleξzwischenx undx0 nicht n¨aher. Daher kann man nicht exakt die Abweichung der N¨ahe- rungsfunktionpn(x)zur Funktionf angeben. F¨ur die konkreten Anwendungen wird diese Tatsache aber keine Rolle spielen, da wir f¨ur das RestgliedR_m(x) eine Obergrenze angeben. Wenn das RestgliedRm(x)^m→∞−→ 0erf¨ullt, so erh¨alt man

Satz ¨uber Taylor-Reihen. Ist f eine in x₀ ∈ ID beliebig oft differen- zierbare Funktion und erf¨ullt das RestgliedRm(x)→ 0 f¨ur m → ∞, so gilt

f(x) = f(x0) +f⁰(x0) (x−x0) + 1

2!f⁰⁰(x0) (x−x0)²+. . . . . .+ 1

n!f⁽ⁿ⁾(x0) (x−x0)ⁿ+. . .

=

∞

X

n=0

1

n!f⁽ⁿ⁾(x0) (x−x0)ⁿ.

Diese Potenzreihe heißt die Taylor-Reihe zur Funktion f am Ent- wicklungspunktx0.

Bemerkungen:

(1) Der Konvergenzradius der Taylor-Reihe ist nicht notwendigerweise>0.

(2) Falls die Taylor-Reihe vonf konvergiert, muss sie nicht notwendigerweise gegenf(x)konvergieren.

(3) Die Taylor-Reihe konvergiert genau dann gegenf(x), wenn das Restglied R_m(x)f¨urm→ ∞ gegen Null geht. In diesem Fall stimmen die Funktion