Active distribution networks or microgrids? Optimal design of resilient and flexible distribution grids with energy service provision

Research Collection

Journal Article

Active distribution networks or microgrids? Optimal design of resilient and flexible distribution grids with energy service provision

Author(s):

Wu, Raphael; Sansavini, Giovanni Publication Date:

2021-06

Permanent Link:

https://doi.org/10.3929/ethz-b-000475935

Originally published in:

Sustainable Energy, Grids and Networks 26, http://doi.org/10.1016/j.segan.2021.100461

Rights / License:

Creative Commons Attribution 4.0 International

This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use.

ETH Library

Sustainable Energy, Grids and Networks 26 (2021) 100461

Contents lists available atScienceDirect

Sustainable Energy, Grids and Networks

journal homepage:www.elsevier.com/locate/segan

Active distribution networks or microgrids? Optimal design of resilient and flexible distribution grids with energy service provision

Raphael Wu, Giovanni Sansavini

Reliability and Risk Engineering Laboratory, Institute of Energy and Process Engineering, Department of Mechanical and Process Engineering, ETH Zurich, Leonhardstrasse 21, 8092 Zurich, Switzerland

a r t i c l e i n f o

Article history:

Received 14 December 2020

Received in revised form 1 March 2021 Accepted 8 March 2021

Available online 16 March 2021 Keywords:

Power distribution planning Resilience

Optimization

Energy system transition Islanding

Flexibility

a b s t r a c t

Ensuring the continuity of service in electricity distribution grids at minimum costs is a key challenge in many countries, as extreme weather events and fluctuating renewable energy increase. New grid concepts such as active distribution networks with distributed energy resources, or microgrids that can operate in islanded mode, offer opportunities to improve the reliability and resilience of distribution grids. This paper presents an active distribution network design optimization with the option to transition into a microgrid, quantifying reliability and resilience improvements, and considering faults within the network as well as unexpected islanding events, which require fast-ramping distributed energy resources. Flexibility, both of loads and distributed energy resources, is used to provide energy services to the surrounding grid with a detailed and general model. Solving the resulting mixed-integer linear program with Column and Constraint Generation and Surrogate Absolute Value Lagrangian Relaxation decreases the computational time significantly. Case studies and sensitivity analyses provide general results for the reliability and resilience targets entailing the optimum transition to microgrids, and quantify the contribution of energy service provision to reduce overall costs.

©2021 The Authors. Published by Elsevier Ltd. This is an open access article under the CC BY license (http://creativecommons.org/licenses/by/4.0/).

1. Introduction

The proliferation of distributed generators (DG), storage, com- munication and control enables distribution grids to transition from passive to active distribution networks (ADNs) [1]. This transition aims at increasing efficiency and renewable energy, using demand flexibility, and speeding up outage recovery [1].

Furthermore, ADNs are able to offer ancillary or other energy services (ES) [2]. Microgrids (MGs), with their islanding ability [3], are a further step in this transition, adding resilience to distribu- tion grids. Within this paper, resilience is defined as the ability to anticipate, absorb and recover from large disturbances by islanding, whereas reliability is the ability to withstand random faults within the ADN [4].

Transitioning from an ADN to a MG can be a significant trans- formation, depending on parameters such as the amount of dis- tributed energy resources (DER) already installed, reliability and resilience targets, as well as the costs of additional DER, commu- nication, control and protection to enable islanding [3]. Therefore, the decision between a MG and other ADN options should be made carefully, considering all issues and opportunities listed above.

This paper investigates the following research questions:

∗ Corresponding author.

E-mail address: sansavig@ethz.ch(G. Sansavini).

(1) How do reliability and resilience goals influence the opti- mal DER mix and the decision between ADNs or MGs?

(2) How much can ES contribute to incentivize DER invest- ments in today’s markets?

1.1. Microgrid transition: Enabling islanding in ADNs

The vast majority of MG design optimization literature as- sumes that the decision to create a MG is already made [5].

Two exceptions are [6], which evaluates the economic viability of a MG, and papers on partitioning feeders into MGs, which may not be connected to any substation [7], or can island if sufficient DER are already present [8]. None of the papers above consider that adequate DER capacity is not enough to ensure successful islanding. In case of an unexpected external blackout, DER must ramp up within tens of milliseconds [9] to seconds [10]

to prevent a voltage and frequency collapse, depending on control strategies, DER and load types. Droop control and virtual inertia [11] improve ramp-up times to 0.1–1s, which can be achieved with batteries [12] or supercapacitors [13]. Reactive power must also be ramped quickly to ensure successful islanding [14].

In addition to adequate and fast-ramping DER, a prospective MG needs communication, control and protection hardware and software to island [3]. As DER and line investment, communica- tion, control and protection are usually separately planned for ADN [15], most MG planning optimizations consider a subset of

https://doi.org/10.1016/j.segan.2021.100461

2352-4677/©2021 The Authors. Published by Elsevier Ltd. This is an open access article under the CC BY license (http://creativecommons.org/licenses/by/4.0/).

these tasks. In [16], communication hardware and reconfigura- tion switches are co-optimized, but without sizing DER. The cost of protection devices for islanding is considered in [17], albeit without power flow.

Due to the complexity of designing a MG including DER, lines, communication, control and protection, there is no optimization method in literature to design an ADN with the option to transi- tion to a MG. This paper is a first step towards filling this gap, by modeling the decision, technical requirements and cost of transforming an ADN into a MG.

1.2. Energy services

As MGs mostly island during rare disturbances [4], their DER can be used to generate additional revenue by offering ES [18].

Providing ancillary services and reliability reserves is found to be synergistic and improve the business case for MGs [19]. How- ever, [19] neglects power flow. Furthermore, the modeled UK ancillary market does not include energy payments and ES can only be called once per day. MG operation is optimized in [2]

by bidding in day-ahead energy, spinning reserve and flexibility ramping markets, considering payments for ES energy as well as uncertainty in market prices and renewable generation. However, the only constraints on storage are that there should be enough energy to maintain the committed power during a single hour. If the ES gets called for several hours, the storage could be emptied, rendering the MG unable to deliver the service. This problem is addressed in [20], where the available ES capacity is the minimum surplus that can be maintained over 24 h of operation. As [20]

only assesses the capability of MGs to provide ES, payments for ES energy and capacity are not considered.

1.3. Contributions

The key contribution of this paper is to propose a method to enhance the reliability, resilience and economic performance of distribution grids by optimizing the transition from ADNs to MGs. DER are optimally sized and participate in ES, as DER backup power is rarely needed. The following method advancements are achieved:

(1) the decision of transforming an ADN into a MG is modeled within the design optimization, considering the costs of additional equipment, and resilience implications;

(2) successful, unanticipated islanding is ensured by introduc- ing ramping constraints for active and reactive power, with potential shedding of low priority loads;

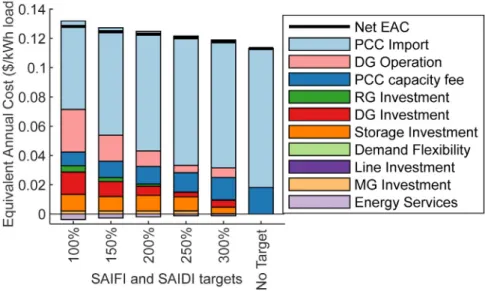
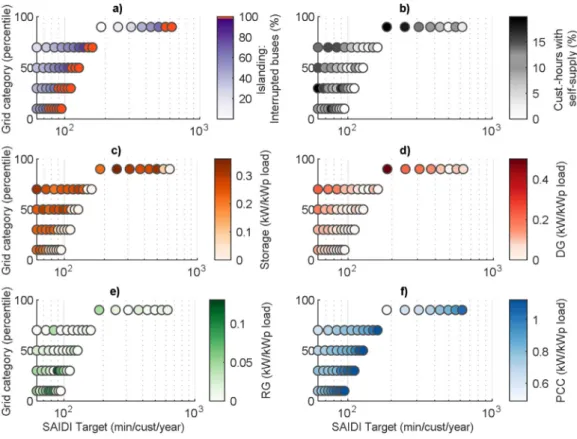
(3) constraints on established quality indices, i.e. SAIFI and SAIDI, are introduced, and we show that they can quan- tify reliability and resilience. Target values can be met by installing lines, investing in DER and creating a MG;

(4) a general framework to model ancillary and reliability ser- vices to the surrounding grid is introduced. ES are modeled with power flow, capacity and energy payments, ensuring sufficient stored energy even if the ES can be called during several time intervals per day;

(5) an efficient solving method based on Surrogate Absolute- Value Lagrangian Relaxation (SAVLR [21]) is developed.

1.4. Optimal MG design

Table 1summarizes the MG model [22] upon which the de- veloped models for energy services, for demand flexibility and for reliability and resilience build. To facilitate the understanding, decision variables, constraints and objective function contribu- tions are split into 4 levels containing the optimal design (1)

and operation (2), resilience (islanding events (3)), and reliability (faults within the MG (4)). Despite the hierarchical structure, all variables, constraints and objective contributions are solved in a single optimization problem.

The investment level (1) contains DER installed capacitiesS_max^DER and binary investment variables,y^DER_Inv for DER andy_lfor lines. DER investment costs are approximated as affine functions C_In^DER_v = c^DER_Inv,0y^DER_Inv +c_In^DER_v,SS_max^DER, with fixed (c_In^DER_v,0) and capacity-dependent costs (c_In^DER_v,S). The rated PCC power has a cost ofC_Cap^PCC =c_Cap^PCCS_max^PCC. The total investment and operation costs are

C_Inv=∑

DER

C_In^DER_v +∑

l

C_l,Inv+C_Cap^PCC (1)

C_Op=

T

∑

t=₁

wt

(

C_Op^PCC_,t+∑

DER

C_Op^DER_,t+∑

RG

C_Curt^RG_,t )

(2)

DER operation in level (2) is modeled with the activeP_t^DER and reactive power Q_t^DER produced. Storage includes stored energy variablesE^Str_t , and constraints on charging, discharging and aging.

Power flow is modeled with linearized DistFlow and radiality constraints [22], power balances at each bus and capacity limits.

To reduce the computational effort, a representative day method [22] is used. In the operations cost (2), wt is the number of represented days per year.

Stochastic islanding events in level (3) are modeled as separate scenarios, beginning at each time step t. All constraints and variables of level (2) are repeated for each islanding scenarioi.

The power exchanged at the PCC is set to zero, and storages are initialized at the energy level before islanding.

Faults within the MG in level (4) are modeled using line failure ratesλl and repair durationsτl. The outage frequencyλ^Dmd_Fl ^and expected durationU_Fl^Dmdat each demand busDmdare calculated using binary variablesy^Dmd_l andy^Dmd_l , which are constrained to be 1 for the path between the PCC and each demand bus [22]. SAIFI and SAIDI are calculated using binary variables _y˜^Dmd

NS,t and _y˙^Dmd

NS,t, indicating the time steps during which demand exceeds supply at every bus:

λ^Dmd_Fl =λ^Dmd+∑

l

(y^Dmd_l +y^Dmd_l )

λl ∀Dmd (3)

U_Fl^Dmd=λ^Dmdτ^Dmd+∑

l

(y^Dmd_l +y^Dmd_l )

λlτl ∀Dmd (4)

SAIDI= (

∑

Dmd

n^Dmd_CustU_Fl^Dmd∑

t

y˜^Dmd_NS,t/^T )

/∑

Dmd

n^Dmd_Cust (5)

SAIFI= (

∑

Dmd

n^Dmd_Custλ^Dmd_Fl ∑

t

˙y^Dmd_NS,t/^T )

/∑

Dmd

n^Dmd_Cust (6)

wheren^Dmd_Cust is the number of customers per bus.

The remainder of this paper is organized as follows: Sections2 and3introduce the proposed ADN and MG design optimization and the solution method. Section4introduces the case study. Sec- tion5discusses the resulting optimal ADN and MG designs and highlights the improvements of the proposed approach compared to literature. Section6concludes.

2. Proposed optimization model

The proposed ADN design optimization model including the investment and operation of DER and lines, considering reliability, demand flexibility, ES as well as the option to transform the ADN into a MG, is presented in the problemP1:

P1:O₁=minC_Inv+C_Op+C_DF+y^MG_Invc^MG_Inv −I_ES (7) s.t. the constraints inTable 1,(1)–(2),(5)–(6),(8)–(44)

2

R. Wu and G. Sansavini Sustainable Energy, Grids and Networks 26 (2021) 100461

Table 1

Summary of the 4-level MG optimization model in [22], which is expanded in this paper.

Model level Decision variables Constraints Objective contribution

(1) Investment - DER capacitiesS_max^DER,E_max^Str - Binary investmentyl,^yDERInv - PCC capacityS^PCC_max

- Discrete investment options (lines) - Fixed cost constraints

- Line investment costCl,Inv - DER investment costC_In^DER_v (2) Operation - DER powerP_t^DER,Q_t^DER

- Storage charging/ discharging powerP_ch^Str_,t,P^Str_di,t - Stored energyE_t^Str

- Power flows, voltagesPl,t,^Ql,t,^Vb²,t

- PCC importP_t^PCC,Q_t^PCC

- DER, PCC and line capacity limits - Minimum part loads (DG) - Available energy (RG) - Energy balances (Str) - Str Cycling limits - DistFlow equations - Radiality constraints

- Nodal power balances with demandsS_t^Dmd

- DER Operations costC_Op^DER_,t - RG curtailment penaltyC_Curt^RG_,t - PCC import costC_Op^PCC_,t

(3) Resilience - DER powerP_t^DER,Q_t^DER

- Storage charging/ discharging powerP_ch^Str_,t,P^Str_di,t - Stored energyE_t^Str

- Power flows, voltagesPl,t,^Ql,t,^Vb²,t

- PCC importP_t^PCC,Q_t^PCC

- Zero PCC power - Str energy continuity

- Cost of redispatchCRes

(4) Reliability - Path variablesy^Dmd_l ,^yDmdl

- Net demandP_net^Dmd_,t

- Indicators that Dmd cannot supply itselfy˜^Dmd_NS,t,y˙^Dmd_NS,t

- Path modeling between Dmd and PCC - Active and apparent power limits on DER supplying their bus

- Cost of demand not suppliedCRel

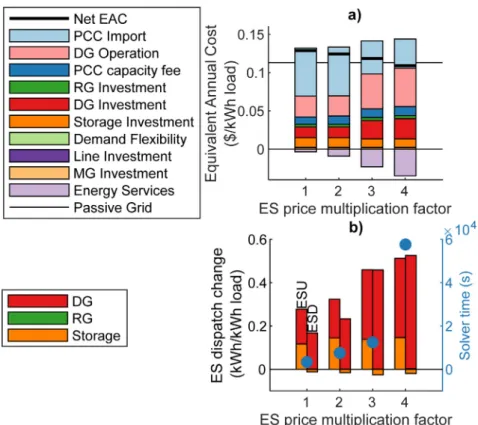
P1 minimizes the equivalent annual cost [22] of investment C_Invand operationC_Opof lines, DER, and PCC electricity, the cost of activating demand flexibilityC_DF and the cost of transforming the ADN to a MG, expressed by a binary variabley^MG_Invand the costc_In^MG_v. AsP1 is a minimization, the ES incomeI_EShas a negative sign. The modeling and objective contributions of ES, demand flexibility and the microgrid transition are described in Sections2.1,2.2and 2.3, respectively.

2.1. Energy services

To capture reliability services [19] as well as ancillary service markets [23], the following general ES framework is modeled: For each market time intervalt^ES, the ADN offers a capacity to absorb or provide power. The effectively provided power is uncertain, as dispatch decisions are made externally, e.g. by the transmission system operator (TSO). To ensure that the ADN can provide the offered power, the maximum ramp up (ESU) and ramp down (ESD) ES cases are modeled as separate scenarios, subject to all constraints inTable 1, level (2). The resulting PCC import power, P_ESU^PCC_,t for the ESU and P_ESD^PCC_,t for ESD, is used to determine the available ES capacity:

P^ESU

t^ES ≤P_t^PCC−P_ESU^PCC_,t ∀t^ES,^t∈t^ES (8) P_t^ESDES ≤P_ESD^PCC_,t−P_t^PCC∀t^ES,^t∈t^ES (9) whereP^ESU

t^ES andP^ESD

t^ES are the available capacities for ESU and ESD respectively. In(8), the offered ES capacity is the minimum differ- ence between the originally planned importP_t^PCCand the reduced ESU power importP_ESU^PCC_,t. As ES dispatch can empty or fill storages completely, the available ES capacities can become negative, thus the ADN should not offer ES during that time. Therefore, binary variables y^ESU

t^ES and y^ESD

t^ES are introduced, indicating that the ADN is offering ES. The following constraints ensure that ES are only offered if the available capacity is nonnegative, and model the ADN incomeI^ESU

P,t^ES and I^ESD

P,t^ES for offering ES capacity with prices c^ESU

P,^tESfor ESU andc^ESD

P,^tES for ESD:

I^ESU

P,t^ES=c^ESU

P,t^ESP^ESU

t^ESy^ESU

t^ES ∀t^ES (10)

I^ESD

P,t^ES=c^ESD

P,t^ESP^ESD

t^ESy^ESD

t^ES ∀t^ES (11)

I_P^ESU_,tES,^I_P^ESD_,tES≥0∀t^ES (12) ES energy is priced atc_En^ESU_,t andc_En^ESD_,t. As the dispatch is uncer- tain, energy payments can range between zero and the maximum

dispatchc_En^ESU_,t(

P_t^PCC−P_ESU^PCC_,t)

for ESU. For a conservative estimate, the energy costC^ESU

En,t^ES are constrained as:

C^ESU

En,t^ES≥0∀t^ES (13)

C^ESD

En,t^ES≥0∀t^ES (14)

C_En^ESU_,tES≥∑

t∈_t^ES

(

∑

DER

(C_Op^DER_,ESU,t−C_Op^DER_,t)

−c_En^ESU_,t∗(

P_t^PCC−P_ESU^PCC_,t) )

−M(1−y^ESU

t^ES)∀t^ES (15)

C_En^ESD_,tES≥∑

t∈t^ES

(

∑

DER

(C_Op^DER_,ESU,t−C_Op^DER_,t)

−c_En^ESD_,t∗(

P_t^PCC−P_ESD^PCC_,t) )

−M( 1−y^ESD

t^ES

) ∀t^ES (16)

If the TSO requires no ESU,(13)is binding. The cost for maximum ESU dispatch in (15) is the difference in DER operations cost

∑

DER

(C_Op^DER_,ESU,t−C_Op^DER_,t)

, from which the energy payment for ES is subtracted. If the ADN is not offering ES, (15) is relaxed by

−M(1−y^ESU

t^ES) with a sufficiently large M [24]. The ESD case is treated analogously in(14),(16).

The total ES incomeI_ES consists of the capacity and energy related costs and revenues, considering the time step weight of each ES market time intervalwt^ES.

I_ES=∑

t^ES

wt^ES

( I^ESU

P,t^ES+I^ESD

P,t^ES−C^ESU

En,t^ES−C^ESD

En,t^ES

)

(17)

This general ES model can be adapted to different ancillary service markets and products, such as frequency containment reserve and frequency restoration reserve in Europe [25], or reg- ulation and reserve services in the USA [26]. The general model allows for asymmetric service provision (P^ESU

t^ES ̸=P^ESD

t^ES), however, symmetric provision for specific markets [25] can be enforced with the additional constraint P^ESU

t^ES y^ESU

t^ES = P^ESD

t^ES y^ESD

t^ES. While an- cillary services are provided during normal operation, ADNs can offer the flexible capacity to neighboring distribution networks in case of a local blackout [19]. The same ES model(8)–(17)can, therefore, be used to model reliability services.

2.2. Demand flexibility

Flexible demands are modeled using the approach in [27], where a predefined fractionf_A^DF_vl,t of the apparent demandS^Dmd_t can be shifted within a time windowt^DF:

0≤S^DF_fr,t≤f_A^DF_vl,tS_t^Dmd∀Dmd,^{t (18)}

3

0≤S_to^DF_,t ∀Dmd,^{t (19)}

∑

τ∈_t^DF

f_En^DF_,τS_fr^DF_,τ−S^DF_to,τ =0∀Dmd,^{tDF (20)}

S^DF_max≥S_fr^DF_,t ∀Dmd,^{t (21)}

C_DF =∑

Dmd

c_DFS_max^DF (22)

where S_fr^DF_,t is the demand shifted from time t, and S^DF_to,t is the demand shifted to timet. The net demand shifted to timet is denoted asS_t^DF =S_to^DF_,t−S_fr^DF_,t. The demandS_t^Dmd in all constraints in Table 1 is replaced by (S_t^Dmd +S_t^DF), which is the demand including flexibility. The cost of activating demand flexibilityC_DF in(22)is proportional to the maximum demandS_max^DF shifted away from any time. This cost can model situations where the ADN planner invests in devices to control flexibility at each demand bus [27], or reflect existing demand response markets where flexible demands are paid for the offered capacity [28].

2.3. Microgrid transition, reliability and resilience

To model the transformation of an ADN into a MG, two deci- sions are modeled: First, a binary variabley^MG_Inv indicates whether the necessary control, communication and protection equipment for islanding is installed. Second, there might be priority de- mandsDmd^Pr which should always be supplied during islanding, whereas other loads can be shed. Therefore, a binary variabley^Dmd_Sh is introduced, and constrained to be 1 if the demandDmdis shed while islanding:

y^Dmd_Sh ≥1−y^MG_Inv ∀Dmd (23)

y^Dmd_Sh =1−y^MG_Inv ∀Dmd^Pr (24)

While(23)ensures that all demands are shed during islanding if the MG is not built (y^MG_Inv =0),(24)indicates that if the MG is built, demandsDmd^Pr must not be shed when islanding. Using y^Dmd_Sh , constraints(3)and(4)are replaced by:

λ^DmdFl =λ^IslyDmdSh +λ^Dmd+∑

l

(y^Dmd_l +y^Dmd_l )

λl∀Dmd (25)

U_Fl^Dmd=U^Isly^Dmd_Sh +λ^Dmdτ^Dmd+∑

l

(y^Dmd_l +y^Dmd_l )

λlτl∀Dmd

(26) whereλ^Islis the rate andU^Islis the expected duration of islanding events. Including islanding in the nodal outage rate and duration enables buses with DER to self-supply, irrespective of the fault location and whether a MG is built or not. Load shedding while islanding is only enabled ify^Dmd_Sh =1:

S^Dmd_NS,i,t ≤M_t^Dmdy^Dmd_Sh ∀Dmd,ⁱ,^{t (27)} where S^Dmd_NS,i,t is the demand not supplied during islanding, and M_t^Dmd≥S_t^Dmd+S_t^DF is a sufficiently large parameter (Big-M [24]).

The combination of(24)and (27)sets the demand not supplied to zero for all priority loads when a MG is built, whereas(25)–

(27)ensure that if a load is shed (S_NS^Dmd_,i,t >^{0, thusyDmd}_Sh =1), the corresponding contribution from islanding events is added to the nodal outage rate and duration.

This model is advantageous because targetsSAIFI_max,SAIDI_max on total SAIDI and SAIFI can be imposed, whether the faults occur inside or outside the ADN or MG:

SAIFI≤SAIFI_max (28)

SAIDI≤SAIDI_max (29)

2.3.1. DER ramping for islanding transitions

To prevent a blackout when islanding unexpectedly, there must be sufficient fast-ramping DER in a MG. The DER ramping capability is modeled using the variablesP_RU^DER_,t,P_RD^DER_,t,Q_RU^DER_,t,Q_RD^DER_,t, with active and reactive ramp-up (RU) and ramp-down (RD) capacities. Ramping power is limited by:

P_RU^DER_,t,^P_RD^DER_,t,^Q_RU^DER_,t,^Q_RD^DER_,t ≥0∀DER,^{t (30)} P_r^DER_,t ≤f_P^DER_,r S_max^DER ∀DER,^t, ^r∈ {RU,^RD} (31) Q_r^DER_,t ≤f_Q^DER_,rS_max^DER ∀DER,^t, ^r∈ {RU,^RD} (32)

(P_t^DER+P_RU^DER_,t)2

+(

Q_t^DER+Q_RU^DER_,t)2

≤( S_max^DER)2

∀DER,^{t (33)} (P_t^DER+P_RU^DER_,t)2

+(

Q_t^DER−Q_RD^DER_,t)2

≤( S_max^DER)2

∀DER,^{t (34)} P_r^DER_,t ≤My^DER_Op,t ∀DER,^t, ^r∈ {RU,^RD} (35) Q_r^DER_,t ≤My^DER_Op,t ∀DER,^t, ^r∈ {RU,^RD} (36) All ramping powers are nonnegative (30), and are limited by each DER’s fast ramping capability, which is proportional to the installed capacityS_max^DERwith factors f_P^DER_,r ,^fQ^DER,^r ∈ [0,¹]. Apparent power limits(33)–(34)must be respected when the DER power changes toP_t^DER+P_RU^DER_,t,Q_t^DER+Q_RU^DER_,t,P_t^DER−P_RD^DER_,torQ_t^DER−Q_RD^DER_,t after islanding. As the active power of most DER is nonnegative, P_RD^DER_,tis omitted in(33)–(34), because it can only reduce the appar- ent power magnitude. DER which are not permanently online can only contribute to ramping if they are already operating (y^DER_Op,t = 1), which is enforced with the Big-M constraints(35)–(36)[24].

Storage ramping is additionally constrained by:

(P_t^Str−P_RD^Str_,t)2

+(

Q_t^Str+Q_RU^Str_,t)2

≤( S_max^Str)2

∀Str,^{t (37)} (P_t^Str−P_RD^Str_,t)2

+(

Q_t^Str−Q_RD^Str_,t)2

≤( S_max^Str)2

∀Str,^{t (38)} P_RD^Str_,t≤(

E_max^Str −E^Str_t )

/⁽ηchT_RD^Str)+P_di^Str_,t ∀Str,^{t (39)} P_RU^Str_,t≤(

E_t^Str−(

1−DOD^Str_max) E^Str_max)

ηdi/^TRU^Str+P_ch^Str_,t ∀Str,^{t (40)} The storage powerP_t^Str=P_di^Str_,t−P_ch^Str_,tis positive when discharg- ing. As storage can have negative active power, P_RD^Str_,t has to be considered in the apparent power limits(37)–(38). Furthermore, the storage ramping power is limited by energy limits(39)–(40).

According to(39), the storage output power can be reduced if the storage is currently discharging (P_di^Str_,t >0), or if there is enough energy capacity left to charge the storage during the ramping timeT_RD^Str.(

E^Str_max−E^Str_t )

/ηchis the remaining energy which can be charged, considering the charging efficiencyηch. Eq.(40)enables the storage to ramp up whenever it is charging (P_ch^Str_,t > ^{0), and} if there is enough energy left without discharging beyond the maximum depth of dischargeDOD^Str_max, considering the discharge efficiencyηdi. The impact of ramping events on storage energy levels in subsequent time steps is neglected, as ramping events are very short compared to the operating time step lengths.

With all DER ramping capabilities defined, the MG ramping requirements are expressed as(41)–(44):

f_P,RUP_t^PCC≤∑

DER

P_RU^DER_,t+∑

Dmd

y^Dmd_Sh (P_t^Dmd+P_t^DF)+M(1−y^Mg_Inv)∀t

(41) f_Q,RUQ_t^PCC ≤∑

DER

Q_RU^DER_,t+ ∑

Dmd|_Qt^Dmd>0

y^Dmd_Sh (Q_t^Dmd+Q_t^DF)

+M(1−y^Mg_Inv)∀t (42) f_P,RDP_t^PCC≥ −∑

DER

P_RD^DER_,t−M(1−y^Mg_Inv)∀t (43)

f_Q,RDQ_t^PCC ≥ −∑

DER

Q_RD^DER_,t− ∑

Dmd|Q_t^Dmd<⁰

y^Dmd_Sh (Q_t^Dmd+Q_t^DF)

4

R. Wu and G. Sansavini Sustainable Energy, Grids and Networks 26 (2021) 100461

−M(1−y^Mg_Inv)∀t (44) Eq.(41)ensures that if the MG is importing power (P_t^PCC >^{0) and} an unexpected islanding transition happens, the MG can cover its power importP_t^PCC with sufficient ramp-up power∑

DERP_RU^DER_,t including a safety factorf_P,RU≥1, while shedding all low priority loads∑

Dmdy^Dmd_Sh (P_t^Dmd+P_t^DF). If no MG is built, the termM(1−y^Mg_Inv) relaxes the PCC ramping requirement. Eq. (42) is the reactive power equivalent of(41), while(43)and (44)model the ramp- down requirements when the MG is exporting (P_t^PCC,^Q_t^PCC <^0).

As the active power demand (P_t^Dmd+P_t^DF) is nonnegative, shedding loads would not help if the MG is exporting power, thus the load shedding term is omitted in(43).

The safety factors f_P,RU, f_P,RD, f_Q,RU and f_Q,RD are greater or equal to 1 and depend on the load types [9], and the load and RG uncertainty [29]. If there is a succession of DER ramping up at different times, several sets of constraints (30)–(44) are used, each modeling a different time window during the islanding transition.

3. Solution method 3.1. Linearization

The optimization problem P1 in (7) contains two kinds of nonlinearities, which are removed to transformP1 into a Mixed Integer Linear Program (MILP). The products of a binary variable yand a continuous variablexin(5),(6),(10),(11),(41)and(42) are replaced by exact linear reformulations [30]:

x−u(1−y)≤z≤x−l(1−y) (45)

ly≤z≤uy (46)

where l is a lower bound on x, u is an upper bound on x, and z is a continuous variable constrained to be equal to the product xy by (45)–(46). Quadratic capacity limits of the form P²+Q²≤S²in(33)–(34),(37)–(38)are replaced by a polygonal inner approximation [22]:

Pcos ((

n−¹ 2

)2π N

) +Qsin

((

n−¹ 2

)2π N

)

+ ≤Scos(π N )

∀n∈ {1,², . . . ,^N} (47)

where N is the number of sides of the polygon.

3.2. SAVLR-CCG solution

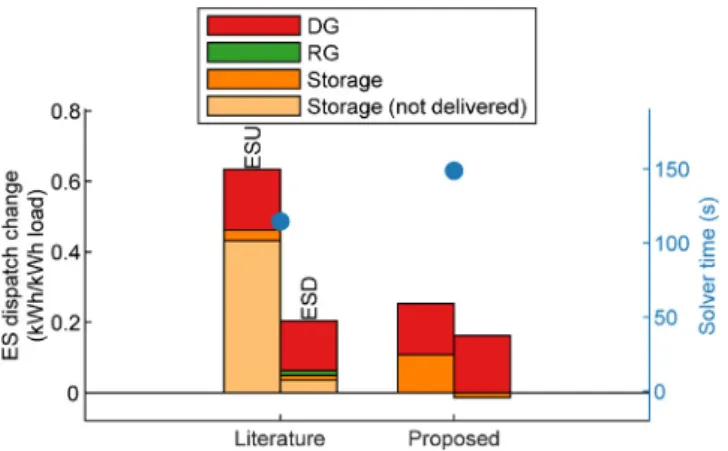
The overall linearized ADN and MG optimization problemP1 in (7) is a stochastic MILP, which becomes prohibitively large to solve. The Column-and-Constraint Generation (CCG) approach in [22] is insufficient to solveP1: State-of-the-art solvers CPLEX and Gurobi [31] reduce the MIP gap to 7%–12% within 4 h for the case study in Section 4, but achieve only 3.5%–8% within 120 h. This lack in progress is related to ES and storage, as the removal of each enables solving P1 to 1% MIP gap in 2 h.

Therefore, a Lagrangian decomposition method is developed. A subproblem without ES calledP2 in(48)–(49), and a subproblem without reliability and resilience calledP3 in(50)–(53)are solved iteratively:

P2:O₂=minC_Inv+C_Op+y^MG_Invc^MG_Inv +λ^Tg( x^Des,^xDesP3

)+c∑

j

q_j

(48) s.^t.the constraints inTable 1

(1)–(2),(5)–(6),(18)–(44)

−q_j≤g(

x^Des,^xDes_P3)

≤q_j (49)

P3:O₃=minC_Inv+C_Op−I_ES+λ^Tg(

x^Des_P2,^xDes) +c∑

j

r_j (50)

s.^t.Constraints of Lev^{els1and2inTable 1} (1)–(2),(8)–(22),

−r_j≤g(

x^Des_P2,^xDes)

≤r_j (51)

∑

DER

S_max^DER≥∑

DER

S^DER_max,P2 (52)

f₁S^DER_max,P2≥S_max^DER≥f₂S_max^DER_,P2∀DER (53) The additional objective terms and additional constraints [21,32]

ensure that P2 and P3 converge to an identical and optimal design: A ‘‘copy-constraint’’ [32] is introduced by setting the functiong(

x^Des_P2,^xDesP3

)in (54)to zero, indicating that the design variables for DER and linesx^Des=[

S_max^DER E_max^Str S_max^PCC y_l]T

inP2 andP3 must be equal:

g( x^Des_P2,^xDesP3

)=x^Des_P2 −x^Des_P3 (54) Using the SAVLR method [21], the violation ofg(

x^Des_P2,^xDesP3

)= 0 is added to the objective functions of P2 and P3, with La- grange multipliersλ. To speed up convergence, the violations of g(

x^Des_P2,^xDes_P3)

= 0,q_j in(49)andr_jin(51), are penalized with a weightc≥0.

The ES income inP3 does not usually lead to sufficient DER investment to ensure the reliability and resilience required inP2.

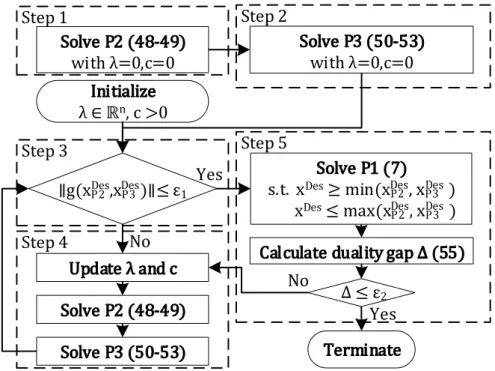
Therefore, adding the surrogate constraints(52)–(53)reduces the number of iterations needed to find a consensus on DER invest- ments betweenP2 andP3. Sufficient DER capacity is guaranteed by(52), whereS_max^DER_,P2is the installed DER capacity inP2 in the most recent iteration. Withf₁>^{1 and 0}≤f₂<^{1,(53)improves} the solver time by limiting the DER capacity changes compared toP2, and by bounding the feasible set ofP3 [33]. To ensure that (52)–(53)do not exclude any optimal solutions,P3 is resolved with increasedf₁, or decreasedf₂as soon as anyS_max^DERreaches one of the limits. The solution procedure is shown inFig. 1.

(1) Solve P2 without the additional objective terms (λ = 0, c=0) to determine the design variablesx^Des_P2. The necessary DER capacitiesS_max^DER_,P2to fulfill the reliability and resilience constraints are saved for the next step.

(2) SolveP3 withλ=0,c=0.

(3) Check the convergence. If

g(x^Des_P2,^xDes_P3⁾

is small enough, go to Step 5, otherwise go to Step 4.

(4) Updateλ^andc[21]. SolveP2 with the latestλ,^c,^xDes_P3^{. Then} solveP3 with the latestλ,^c,^xDes_P2. Go to Step 3.

(5) Find a feasible solution to the full problem by solvingP1 while constrainingx^Desto be within the range of the latest x^Des_P2 and x^Des_P3. Calculate the duality gap ∆^{with(55)[21].}

Stop if the gap is sufficiently small. Otherwise return to Step 3.

The duality gap is calculated as the relative difference between the objective function value ofP1 and the combined objectives of P2 andP3:

∆= ^O1−(

O2+O3−max{

CInv,^P2,^CInv,^P3}

−max{

COp,^P2,^COp,^P3}) O₁

(55) WhereO₁,O₂andO₃are the optimal objective function values ofP1,P2 andP3.O₁is an upper bound on the optimal objective and the rest of the numerator is the lower bound. Because the sumO₂+O₃contains the investment and operations costs twice, the conservative lower bound in(55)is calculated by subtracting the highest investment and operations costs amongP2 andP3.

5