Development and Implementation of New DFT/MRCI Hamiltonians for Odd and Even Numbers of Electrons

Development and Implementation of New DFT/MRCI Hamiltonians for Odd and Even Numbers of Electrons

Inaugural-Dissertation

zur

Erlangung des Doktorgrades der

Mathematisch-Naturwissenschaftlichen Fakultät der Heinrich-Heine-Universität Düsseldorf

vorgelegt von Adrian Heil aus Düsseldorf

Düsseldorf, September 2019

Aus dem Institut für Theoretische Chemie und Computerchemie der Heinrich-Heine-Universität Düsseldorf

Gedruckt mit Genehmigung der

Mathematisch-Naturwissenschaftlichen Fakultät der Heinrich-Heine-Universität Düsseldorf

Berichterstatter:

1. Univ.-Prof. Dr. Christel M. Marian 2. PD Dr. Oliver Weingart

Tag der mündlichen Prüfung:

”Things are only impossible until they are not.”

– Jean-Luc Picard

Eidesstattliche Erklärung

Ich versichere an Eides statt, dass die Dissertation von mir selbst verfasst und ohne un- zulässige fremde Hilfe unter Beachtung der Grundsätze zur Sicherung der guten wissen- schaftlichen Praxis an der Heinrich-Heine-Universität Düsseldorf erstellt worden ist. Die aus fremden Quellen direkt oder indirekt übernommenen Gedanken sind als solche kennt- lich gemacht. Die Dissertation wurde in der vorgelegten oder in ähnlicher Form noch bei keiner anderen Prüfungsbehörde eingereicht. Es wurden keine früheren erfolglosen Promo- tionsversuche unternommen.

Düsseldorf, den 18.9.2019

Danksagung

Zu allererst möchte ich mich bei meiner Doktormutter Prof. Dr. Christel M. Marian für das interessante und neuartige Thema sowie die hilfreichen Diskussionen und die gute Be- treuung bedanken. Auch weiß ich die Gelegenheiten und Möglichkeiten im Rahmen dieser Promotion sowie die Freiheiten und das damit verbundene in mich gesetzte Vertrauen sehr zu schätzen. Ebenfalls möchte ich mich bei PD Dr. Oliver Weingart für die Übernahme des Korreferats, insbesondere auch für die Kurzfristigkeit, sowie für hilfreiche Diskussionen zu Lösungsmitteleffekten bedanken.

Darüber hinaus gilt mein Dank Dr. Martin Kleinschmidt für hilfreiche Diskussionen, ins- besondere zu technischen Fragestellungen.

Bedanken möchte ich mich auch bei Dr. J. Dominik Spiegel und Dr. Igor Lyskov für interessante und angenehme Gespräche und Diskussionen im fachlichen und fachfremden Kontext, sowie bei allen aktuellen und (inzwischen) ehemaligen Mitgliedern des Instituts für Theoretische Chemie und Computerchemie für die schöne gemeinsame Zeit.

Mein besonderer Dank gilt meiner Verlobten Paulina Trusova für die Unterstützung wäh- rend der Promotion und auch für die Geduld, wenn ich am Wochenende ’kurz mal einen Job abschicken’ wollte und es dann doch etwas länger wurde. Ebenfalls danke ich Paulina Trusova sowie Fabian Zillgens für das Korrekturlesen dieser Arbeit.

Der Deutschen Forschungsgesellschaft (DFG) danke ich für die finanzielle Unterstützung dieser Promotion mit der Projektnummer MA-1051/14-2.

Contents

Abbreviations II

List of Publications V

1 Introduction 1

2 Theory 5

2.1 Vertical Transitions and Excited States Processes . . . 5

2.2 Density Functional Theory . . . 6

2.3 Open Shells in Density Functional Theory . . . 9

2.4 DFT Functionals . . . 14

2.5 Configuration Interaction and Electron Correlation . . . 15

2.6 The Combination of DFT and MRCI . . . 19

3 The Datasets for Training and Testing 24 3.1 Dataset for Training . . . 24

3.2 Dataset for Testing . . . 25

3.3 Photoelectron Spectroscopy . . . 26

4 Interface Development 31 4.1 Interface to Dalton . . . 31

4.2 Interface to Orca4.0 . . . 34

5 DFT/MRCI Hamiltonian Development 39 5.1 The R2017 Hamiltonian (Paper 1) . . . 39

5.2 The R2018 Hamiltonian (Paper 2 and 3) . . . 42

6 Application of the New Hamiltonians 49 6.1 C∧N-Platinum Complexes (Paper 4) . . . 49

6.2 Zinc(II) Tripyrrindione Radical (Paper 5) . . . 51

6.3 Blatter Radical (Paper 3) . . . 54

6.4 Triarylamine-Perchlorotriphenylmethyl Radicals . . . 59

6.5 TTM-1Cz Radical . . . 63

6.6 PAH-DTDA Radicals . . . 65

7 Conclusion 69

References 72

Included Papers 82

II

List of Abbreviations

2-MeTHF 2-Methyltetrahydrofuran

acac Acetylacetonate

ADC(2) Algebraic-Diagrammatic Construction bzq Benzo[h]quinolinyl

CASSCF Complete Active Space Self-Consistent Field

CC Coupled Cluster

CC2 Approximate Coupled-Cluster Singles and Doubles

CC3 Approximate Coupled-Cluster Singles, Doubles and Triples CCSD Coupled-Cluster Singles and Doubles

CI Configuration Interaction

CIS Configuration Interaction Singles dbq Dibenzo[f,h]quinolinyl

DCM dichloromethane

DFT Density Functional Theory DFT/MRCI Combined DFT and MRCI DFT/MRSOCI Combined DFT and MRSOCI dpm Dipivolylmethanoate

DTDA 1,2,3,5-Dithiadiazolyl

ES Excited State

eV Electronvolt

FC Franck-Condon

FCA Frozen Core Approximation

GS Ground State

HDOMO Highest Doubly Occupied Molecular Orbital HEG Homogenous Electron Gas

HF Hartree-Fock

III

HOMO Highest Occupied Molecular Orbital

IC Internal Conversion

IQE Internal Quantum Efficiency ISC Intersystem Crossing

K Kelvin

KS Kohn-Sham

LC Ligand Centred

LCD Liquid Crystal Display LED Light Emitting Diode

LSDA Local Spin Density Approximation LUMO Lowest Unoccupied Molecular Orbital

LYP Lee, Yang, Parr

MAE Mean Absolute Error

MaxAE Maximum Absolute Error

MC-PDFT Multiconfiguration Pair-Density Functional Theory MCTDH Multiconfigurational Time-Dependent Hartree

MeCN Acetonitrile

MRCI Multireference Configuration Interaction

MRSOCI Multireference Spin-Orbit Configuration Interaction MRMP2 Multireference PT2

NGA Non-Separable Gradient Approximation

nm Nanometre

OLED Organic Light Emitting Diode PAH polycyclic aromatic hydrocarbons

PBE Perdew, Burke and Enzerhof pure functional PCTM Perchlorotriphenylmethyl

PES Potential energy surface

pm Picometre

IV

ppy 2-Phenylpyridyl

QM/MM Quantum mechanics/ molecular mechanics RASSCF Restricted Active Space Self-Consistent Field rISC Reverse Intersystem Crossing

RMSE Root-Mean-Square Error RODFT Restricted Open-Shell DFT

RT Room Temperature - 298 K

SOMO Singly Occupied Molecular Orbital

TARA Triarylamine

TDHF Time-Dependent Hartree-Fock

THF Tetrahydrofuran

TTM Tris(2,4,6-trichloro)methyl UKS Unrestricted Kohn-Sham VWN Vosko, Wilk, Nusair

WFT Wave Function Theory

ZPE Zero-Point Energy

V

List of Publications

Included as part of this thesis:

1. DFT/MRCI Hamiltonian for odd and even numbers of electrons.

Adrian Heil and Christel M. Marian, J. Chem. Phys., 147, 194104 (2017)

Own contribution: Development and implementation of the R2017 Hamiltonian;

collection of experimental vertical excitation energies of open-shell molecules for training and testing; quantum chemical calculations; statistical evaluation; creation of figures; first draft of manuscript

2. On the performance of DFT/MRCI Hamiltonians for electronic excitations in tran- sition metal complexes: The role of the damping function.

Adrian Heil, Martin Kleinschmidt and Christel M. Marian, J. Chem. Phys., 149, 164106 (2018)

Own contribution: Development and implementation of the R2018 Hamiltonian;

collection of some of the experimental vertical excitation energies of transition metal complexes for testing; quantum chemical calculations; creation of figures; statistical evaluation; first draft of manuscript

3. The DFT/MRCI method.

Christel M. Marian, Adrian Heil and Martin Kleinschmidt. WIREs Comput. Mol.

Sci., 9, e1394 (2019)

Own contribution: Section on the benchmark of transition metal complexes; section on radicals; quantum chemical calculation of the Blatter radical; creation of figures;

statistical evaluation

4. Structure-Emission Property Relationships in Cyclometalated Pt(II) β-Diketonate Complexes.

Adrian Heil and Christel M. Marian, Inorg. Chem., 58, 6123 (2019)

Own contribution: Section on (C∧N) Pt Complexes; Quantum chemical calcula- tions of (C∧N) Pt Complexes; supplemental material; creation of figures

5. DFT/MRCI-R2018 Study of the Photophysics of the Zinc(II) Tripyrrindione Rad- ical: Non-Kasha Emission?

Adrian Heil and Christel M. Marian, Phys. Chem. Chem. Phys., accepted (2019) DOI:10.1039/C9CP04244J

Own contribution: Quantum chemical calculations; creation of figures; first draft of manuscript

VI

Not included as part of this thesis:

1. On the photophysics of four heteroleptic iridium(III)phenylpyridyl complexes invest- igated by relativistic multi-configuration methods.

Adrian Heil, Kathleen Gollnisch, Martin Kleinschmidt and Christel M. Marian, Mol.

Phys., 114, 407–422 (2016)

Own contribution: Quantum chemical calculations on the cis Ir-complexes; creation of figures

2. Simulation of X-ray absorption spectra using core-valence separated DFT/MRCI.

Issaka Seidu, Simon P. Neville, Martin Kleinschmidt, Adrian Heil, Christel M.

Marian, and Michael S. Schuurman, J. Chem. Phys., accepted (2019)

Own contribution: Supply of and instructions to the Dalton interface for open-shell calculations with the DFT/MRCI program; corrections in the draft

VII

Abstract

DFT/MRCI is a well-established semi-empirical quantum chemical method originally developed by Grimme and Waletzke [J. Chem. Phys., 111, 5645 (1999)]. Recently, a redesigned DFT/MRCI Hamiltonian, named R2016, was developed by Lyskov et al. [J. Chem. Phys., 144, 034104 (2016)]

to improve the treatment of bi-chromophores.

Up until now the DFT/MRCI method was limited to closed-shell systems. In this thesis, the R2016 Hamiltonian of Lyskov et al. was successfully extended to open-shell systems based on restricted open-shell Kohn-Sham orbitals as the anchor configuration. The necessary orbitals are calculated with the Dalton program, for which an interface to the DFT/MRCI program was developed.

Experimental electronic excitation energies of doublet states have been gathered from literature, since a collection of these states suitable for testing and training a parameter set does not exist. The new Hamiltonian, named R2017, is able to match the accuracy and computational performance on closed-shell and open-shell organic molecules that was achieved by the previous Hamiltonians on closed-shell molecules. The resulting accuracy, expressed as the root-mean-square error (RMSE), is below 0.2 eV.

While all DFT/MRCI Hamiltonians provide good results on organic molecules, a benchmark of transition metal complexes found an underestimation of vertical excitation energies, especially with the R2016 and R2017 Hamiltonians. The cause could be traced back to the off-diagonal damping function employed in both redesigned Hamiltonians. These findings instigated the development of a new Hamiltonian based on the R2017 Hamiltonian with improved vertical excitation energies for transition metal complexes, dubbed R2018 Hamiltonian. The RMSE of organic transition metal complexes is improved to 0.15 eV from the previously achieved accuracy of 0.20 and 0.25 eV of the original and R2016 Hamiltonians, respectively. The R2018 Hamiltonians provides the highest accuracy on organic transition metal complexes among the four Hamiltonians and matches the accuracy of the original Hamiltonian on inorganic transition metal complexes with considerable improvements over the R2016 and R2017 Hamiltonians. The previously achieved good results on organic molecules are retained, making the new Hamiltonian suitable for a broad range of applications.

The two new Hamiltonians, R2017 and R2018, are applied to a range of molecules and transition metal complexes with odd and even numbers of electrons. In general, a good agreement with the experimentally observed photophysical properties is achieved. The results of the computations can be used to assign electronically excited states and interpret and elucidate relaxation pathways following electronic excitation.

Apart from the successful applications, the new Hamiltonians show an overestimation of transition energies in all calculated polychlorinated triphenylmethyl radicals. The results and potential origin of the errors are discussed.

VIII

Zusammenfassung

DFT/MRCI ist eine etablierte semiempirische quantenchemische Methode, die ursprünglich von Grimme und Waletzke [J. Chem. Phys., 111, 5645 (1999)] entwickelt wurde. Kürzlich wurde ein überarbeiteter DFT/MRCI Hamiltonoperator (R2016) von Lyskov et al. [J. Chem. Phys., 144, 034104 (2016)] entwickelt, um die Beschreibung von Bichromophoren zu verbessern.

Die Anwendung der DFT/MRCI-Methode war bisher auf geschlossenschalige Systeme limitiert. In dieser Doktorarbeit wurde der R2016 Hamiltonoperator von Lyskov et al. erfolgreich um offenscha- lige Systeme erweitert, deren Ankerkonfiguration aufrestricted open-shell Kohn-Sham-Orbitalen basiert. Die dafür notwendigen Orbitale werden mit dem Programm Dalton berechnet, für das ei- ne Schnittstelle zum DFT/MRCI-Programm entwickelt wurde. Experimentelle elektronische Anre- gungsenergien von Dublettzuständen wurden aus der Literatur zusammengestellt, da ein Datensatz dieser Zustände, der zum Anpassen und Testen eines Parametersatzes geeignet wäre, nicht existiert.

Mit dem neuen Hamiltonoperator (R2017) wird dieselbe Genauigkeit und rechnerische Geschwin- digkeit bei geschlossen- und offenschaligen organischen Molekülen erreicht, die von den vorherigen Hamiltonioperatoren für geschlossenschalige Moleküle erreicht wurde. Die Genauigkeit wird durch die Wurzel aus den gemittelten Fehlerquadraten (root-mean-square error, RMSE) angegeben und liegt unterhalb von 0.2 eV.

Während mit allen DFT/MRCI-Hamiltonoperatoren gute Ergebnisse für organische Moleküle er- zielt werden können, wurde in einem Benchmark von Übergangsmetallkomplexen festgestellt, dass die vertikalen Übergangsenergien dieser Systeme unterschätzt werden, insbesondere im Fall der R2016 und R2017 Hamiltonoperatoren. Die Ursache konnte auf die Dämpfungsfunktion der Au- ßerdiagonalelemente zurückgeführt werden, die in den beiden überarbeiteten Hamiltonoperatoren eingesetzt wird. Auf Grundlage dieser Erkenntnisse wurde ein neuer Hamiltonoperator (R2018) entwickelt, der auf dem R2017 basiert und durch eine ausgewogenere Dämpfung die vertikalen An- regungsenergien von Übergangsmetallkomplexen besser beschreibt. Der RMSE reduziert sich für organische Übergangsmetallkomplexe auf 0.15 eV, was eine Verbesserung im Vergleich zum origina- len und R2016 Hamiltonoperator darstellt, die bei 0.20 bzw. 0.25 eV liegen. Mit dem neuen R2018 Hamiltonoperator wird die höchste Genauigkeit für organische Übergangsmetallkomplexe unter den vier Hamiltonoperatoren erreicht. Zusammen mit dem originalen Hamiltonoperator stellt dies die beste Beschreibung anorganischer Übergangsmetallkomplexe dar, was einer deutlichen Verbes- serung der Ergebnisse von R2016 und R2017 entspricht. Die bereits guten Ergebnisse für organische Moleküle werden auch im neuen Hamiltonoperator beibehalten, was eine große Bandbreite an An- wendungsmöglichkeiten eröffnet.

Bei der Anwendung der neuen Hamiltonoperatoren R2017 und R2018 auf eine Reihe von Mole- külen und Übergangsmetallkomplexen mit gerader und ungerader Anzahl von Elektronen wird im Allgemeinen einge gute Übereinstimmung mit experimentell beobachteten photophysikalischen Eigenschaften erreicht. Folglich können die Ergebnisse der Berechnungen dazu verwendet werden, elektronisch angeregte Zustände zuzuordnen sowie Relaxationspfade zu interpretieren und aufzu- klären.

Überschätzungen der Übergangsenergien zeigen sich hingegen in allen berechneten polychlorierten Triphenylmethylradikalen. Die Ergebnisse und die mögliche Ursache der Fehler werden diskutiert.

1 Introduction 1

1 Introduction

In electronic devices and displays, light sources with a good colour profile and a high effi- ciency and longevity are of great importance. For a long time, light emitting diodes (LEDs) based on semiconductors have been used. By altering their crystal structure, changes in the band gap are introduced, which leads to colour variations. In recent years, alternative lighting devices with advantages over LEDs including microLEDs [1, 2], perovskite-based LEDs [3–5] and organic LEDs [6, 7] (OLEDs) have been developed. OLED displays have several advantages over regular LEDs by providing a higher contrast, a higher colour pur- ity, wider viewing angles, faster response times, better power efficiency and true blacks [8].

Displays based on LEDs on the other hand employ a liquid crystal display (LCD) to cover certain colours of each pixel of the white backlighting that is provided by a white LED. In order to provide a practical advantage over LEDs, a high quantum efficiency and stability of the OLED dye is mandatory.

An OLED is composed of an organic material with the ability to emit light under certain circumstances. This material is situated between an anode and a cathode. When a voltage is applied, the organic material is charged. The created electrons and electron- holes recombine in the emission layer of the OLED, where they create an exciton. This exciton decays under emission of electromagnetic radiation.

A very important property to consider in any luminescent exciton is the spin statistics. In the recombination process of an electron-hole pair the resulting state is a singlet with a chance of 25% and a triplet with a chance of 75%, when considering closed-shell species [9].

Since the transition from the excited triplet state to the singlet ground state is a spin- forbidden process, only the 25% singlet population can function as an emitting state.

This limits the internal quantum efficiency (IQE) to 25%. Several approaches exist to circumvent this limitation. One possibility is to employ heavy atoms within the dye which allows the transition from a triplet to the singlet ground state through spin-orbit coupling.

Through this mechanism an IQE of up to 100% is possible [10–12]. An alternative to this triplet harvesting is by repopulating the lowest excited singlet state though reverse intersystem crossing (rISC) from the excited triplet state [13–15].

While all previously discussed possibilities involve closed-shell species, a different way was recently introduced by Peng et al. [16]. By using open-shell species as a dye, the resulting singlet-doublet or triplet-doublet coupled electron-hole pair will – depending on the energy – result in an excited state with one unpaired electron, which can only be a doublet state.

A quartet state, on the other hand, requires three open shells with unpaired spins. The first quartet state is energetically unfavoured compared to doublet states and typically lies energetically above the lowest excited doublet state(s). Therefore, both singlet and triplet excitons can be utilised as the resulting doublet state is energetically favoured. A formation ratio of 100% for a doublet excited state [17] and an external quantum efficiency of 27% [18] have recently been reported for open-shell emitters.

While open-shell systems are prone to dimerisation, disproportionation and interaction with atmospheric oxygen, several stable structures have emerged in recent years [19], of

2 1 Introduction

which some are fluorescent. Tris(2,4,6-trichlorophenyl)methyl radicals with varying sub- stituents – or with one phenyl replaced by a pyridine – are often used in open-shell emitters [16–18, 20–24]. By substituting chlorine with other halogens, the photophysical properties of these radicals can be tuned even further [25]. Other stable fluorescent radicals are based on the Blatter radical [26, 27], 1,2,3,5-dithiadiazolyl (DTDA) radicals that have been linked to aromatic molecules like anthracene and pyrene [28, 29] and the zinc(II) tripyrrindione radical [30]. Nitroxide radicals [31, 32] or lanthanide complexes with chelating nitronyl nitroxide radicals [33] also belong to the group of stable fluorescent radicals.

The calculation and description of excited states are a requirement for the prediction of photophysical properties of (potential) OLED dyes. The reliable description of ex- cited states with good accuracy, however, is a challenging task. Many of the methods used for describing these states start from a converged Hartree-Fock [34–37] (HF) calcu- lation and thus form the group of so-called post-HF methods. Among those are coupled- cluster [38, 39] (CC) methods like CC singles and doubles (CCSD) or approximate singles and doubles [40] (CC2) and approximate CC singles, doubles and triples [41] (CC3). Con- figuration Interaction (CI) in its computationally least-demanding approach as CI singles (CIS) was extended by perturbative doubles to CIS(D) [42]. Other successful methods are the algebraic-diagrammatic construction [43] (ADC(2)), complete active space self- consistent field [44] (CASSCF) and restricted active space self-consistent field [45, 46]

(RASSCF). Staring from the latter two, Møller-Plesset perturbation theory in second or- der [47] (MP2) can be extended to multireference MP2 [48] (MRMP2) or complete active space perturbation theory in second order [49, 50] (CASPT2) for the description of excited states. Hartree-Fock can also be used for excited state calculations as time-dependent Hartree-Fock (TDHF). A different approach, related to TDHF, is the time-dependent density functional theory [51–54] (TDDFT). TDDFT combines a good accuracy for many applications with a low computational demand, allowing excited-state calculations on sys- tems with 50-500 atoms. However, it is limited to single excitations, as is TDHF, making both methods unable to treat states with doubly excited characters.

A different kind of approach seeks a combination of various methods, either to increase the accuracy of a fast method or to lower the computational cost of an accurate method. These combinations make it possible to calculate larger system with good accuracy. One of these approaches combines the semi-empirical orthogonalisation-corrected methods OM1 [55, 56], OM2 [57, 58] and OM3 [59, 60] with MRCI as OMx/MRCI [61, 62]. Other recently developed methods include multiconfiguration pair-density functional theory [63] (MC- PDFT) and the combination of DFT and restricted open shell CI singles (ROCIS) which is called DFT/ROCIS [64, 65]. Among these is also the method that is the focus of this thesis, the combined DFT and MRCI method (DFT/MRCI).

The DFT/MRCI method [66, 67] is a semi-empirical method for computing excited states of closed-shell molecules, depending on a closed-shell determinant. It combines Kohn- Sham (KS) orbitals from DFT with multireference configuration interaction (MRCI). In this approach, the dynamic correlation is computed on DFT level while static correlation is provided by MRCI. Since calculating the dynamic correlation requires a long CI expan- sion, the configuration interaction expansion can be shortened if the dynamic correlation

1 Introduction 3

is already accounted for. To avoid double counting of electron correlation, the integrals are scaled by empirically determined parameters. The advantages of the DFT/MRCI method are a high computational speed with an error less than 0.2 eV, making it pos- sible to calculate photophysical properties of large molecules with a good accuracy [66].

The method was originally developed by Grimme and Waletzke [66]. It represents a gen- eralisation as well as an extension of the previously developed DFT/SCI [68] method, that combines DFT with CI limited to single excitations. From its original release in 1999, the DFT/MRCI method was steadily improved and extended. The parallelisation of the code by Kleinschmidt et al. [69] made it possible to calculate even larger systems in the same amount of time. An extension to include spin-orbit coupling based on the DFT/MRCI wave function was released as a separate program calledSpockCI [70–72] to include properties that are missing in DFT/MRCI due to a spin-free Hamiltonian.

The DFT/MRCI Hamiltonian was redesigned in 2016 by Lyskov et al. [73] to address shortcomings of the original Hamiltonian regarding bi-chromophoric systems that are in- volved in processes like singlet fission or triplet-triplet up-conversion. This Hamiltonian was later named R2016 [67]. By developing a new correction for the matrix elements, a set of four parameters used for all multiplicities represented by an even number of electrons (singlets, triplets, quintets,. . .) was introduced. In the original approach by Grimme and Waletzke, only singlet and triplet multiplicities were possible, using different parameter sets for each multiplicity.

The DFT/MRCI method has been successfully applied in excited states calculations of organic molecules [74–80] and transition metal complexes [81, 82], in excitation energy transfer processes [83, 84], in singlet fission [85] and in benchmark calculations [86–90].

In calculations combining quantum mechanics and molecular mechanics [91] (QM/MM), DFT/MRCI has been successfully employed in the quantum-mechanics region of large biomolecules for calculating vertical excitation energies [92–94]. While these examples demonstrate the broad range of applications, DFT/MRCI lacks the ability to compute vertical excitation energies needed for the emerging field of doublet emitters.

The aim of this thesis is the development of a new DFT/MRCI Hamiltonian capable of treating open-shell as well as closed-shell systems with an error comparable to the original and R2016 Hamiltonian. In order to treat open-shell systems, an anchor configuration based on restricted open-shell Kohn-Sham (ROKS) is required. The ROKS orbitals are calculated with the Dalton program [95]. A new interface between Dalton and DFT/MRCI was needed for the usage of the Dalton program in combination with DFT/MRCI. Due to the advantages of the R2016 Hamiltonian over the original one, the new open-shell Hamiltonian should be based on the R2016 Hamiltonian. A broad and diverse set of experimental excitation energies had to be assembled for developing and testing a new parameter set. The new Hamiltonian is then applied to systems of broader interest to investigate their photophysical properties. All steps outlined above were carried out and are included in this thesis, resulting in the development, implementation and application of a new all-multiplicity Hamiltonian, the R2017 Hamiltonian.

Additionally, it was found that the R2016 and R2017 Hamiltonians and to a smaller degree

4 1 Introduction

also the original Hamiltonian underestimate the vertical excitation energies in transition metal complexes. A new damping function for off-diagonal matrix elements greatly im- proved these excitation energies. Together with a newly optimised parameter set, the all-multiplicity R2018 Hamiltonian was developed and implemented.

This thesis is divided into five sections:

1. The first part introduces the theoretical framework on which the DFT/MRCI method and the development of a new Hamiltonian are based. This includes DFT in general and for open-shell systems, MRCI and CI matrix elements and the previous devel- opments of DFT/MRCI, namely the original development of Grimme and Waletzke and the redesign by Lyskov et al.

2. The second part introduces the datasets that play an important role in the train- ing (parametrisation) and testing of the DFT/MRCI Hamiltonians. The sets are composed of organic molecules and transition metal complexes.

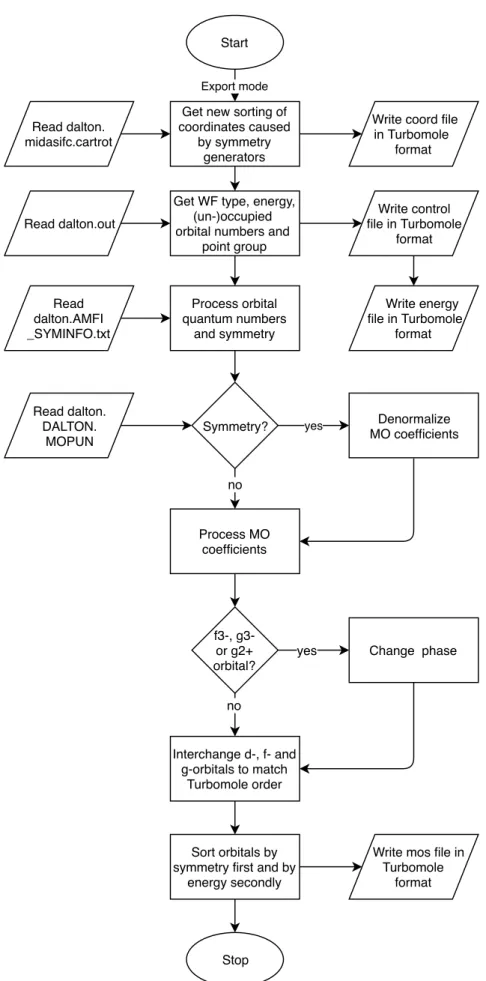
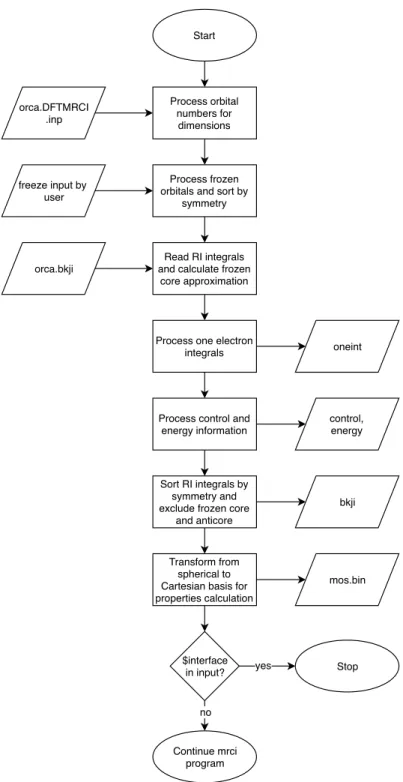
3. The third part introduces the two interfaces to the DFT/MRCI program developed over the course of this thesis. The first interface is needed for transforming the ROKS orbitals calculated with the Dalton program to Turbomole format. Tur- bomole lacks the ability to compute ROKS orbitals and the DFT/MRCI program is interfaced against Turbomole. This interface is named d2tm. The second interface is implemented in the DFT/MRCI program and makes it possible to read the integ- rals and molecular data following aOrca 4.0 [96, 97] DFT single-point calculation.

The Orca program provides RI-integrals and orbitals for closed-shell molecules, thus making the DFT/MRCI program available to a broader audience within the scientific community.

4. The fourth part describes the development and parametrisation of the new Hamilto- nians, dubbed R2017 and R2018, and the assessment of the accuracy. In this section the effect of the off-diagonal damping on the correlation energy is discussed.

5. In the last part, the R2017 and R2018 Hamiltonians are applied to various systems, including closed-shell transition metal platinum complexes and open-shell doublet emitters. The doublet emitters include the zinc tripyrrindione complex, the Blatter radical, PAH-DTDA radicals and molecules based on the triphenylmethyl radical.

2 Theory 5

2 Theory

2.1 Vertical Transitions and Excited States Processes

Vertical transitions are based on the Franck-Condon principle [98–100] that states that the geometry relaxation is much slower than the change in the electronic structure following a (de)excitation process. While the electronic structure undergoes a change during the process, the relaxation of the geometry is delayed. Since there is no change in geometry, the (de)excitation transition is assumed to be a vertical transition. The Franck-Condon principle is employed within the DFT/MRCI calculations, where absorption from the ground state is based on the ground-state geometry and emission from an excited state is calculated at the minimum of the corresponding excited state. Besides vertical transi- tions, important measures are adiabatic transitions that describe the energy between two states at their corresponding relaxed geometry and 0-0 transitions that are based on the adiabatic energy and include the zero-point energy of each state. All these transitions are considered to absorb or emit energy in form of electromagnetic radiation. Besides photo- excitation, other possibilites to access the excited state include photoelectron emission (see Sec. 3.3) and electroluminescence.

The processes involving excited states are represented schematically as a Jablonski dia- gram in Fig. 1. After excitation, the geometry relaxes vibronically (brown arrow). From here, several radiative and non-radiative processes compete. These include non-radiative processes such as internal conversion (IC) and intersystem crossing (ISC). IC describes an iso-energetic transition from one excited state to a higher vibrational level of a differ- ent electronic state without change in multiplicity. The same process but with a change in multiplicity is the ISC. Kasha’s rule [101] states that emission stems from the lowest

Q

D

D

D

Figure 1: Jablonski diagram showing the radiative and non-radiative processes in an open-shell system. The horizontal dark-blue arrows represent the internal conversion (IC) and the olive arrows the intersystem crossing (ISC). The brown arrows indicate the vibrational relaxation within an excited state. The red arrows represent fluorescence and the blue phosphorescence. The green arrows mark the absorption from the ground state to various excited states.

6 2.2 Density Functional Theory

Table 1: Typical time scales of excited state processes [102]. The two rates for internal conversion refer to a fast and a slow rate. The fast rate takes place between excited states (ES), for example D2 →D1whereas the slow rate describes the depopulation to the ground state (GS), for example D1 →D0. All transitions given below are examples referring to doublet (and quartet) states but can occur with the same rates in any analogue case like singlet (and triplet) states.

Process Transition Rate [s⁻¹]

Absorption D0 → Dn 10¹⁵

Solvent reorganisation 10¹²–10¹³

Internal conversion (ES) Dn → D1 10¹⁰–10¹⁴ Vibrational relaxation Dn,ν=n → Dn,ν=0 10¹⁰–10¹²

Fluorescence D1 → D0 10⁷–10⁹

Internal conversion to GS D1 → D0 10⁶–10⁷ Intersystem crossing Qn → Dn 10⁵–10⁸ Phosphorescence Q1 →D0 10⁻²–10³

excited state of each multiplicity, which is shown in Fig. 1 in red (fluorescence) and blue (phosphorescence). While Kasha’s rule predicts emission from the lowest excited state, this does not necessarily mean that there is an emission measurable, as non-radiative de- cay to the ground state via IC or ISC is also possible. The Jablonski diagram depicts a high-lying Q1 excited state above several excited doublet states, which is usually the case in open-shell species. Quartet states require at least three open shells with same-spin electrons while a doublet state requires only one unpaired electron. This is different from closed-shell systems, where excited singlet and triplet states both require two open-shell electrons, with the opposite spins for a singlet and with same spins for a triplet. Due to the exchange energy, the first excited triplet state is typically energetically below the first excited singlet state. In the recombination process of an electron-hole pair, the lowest singlet and triplet state are therefore energetically accessible. In an open-shell species on the other hand, a energetically low-lying doublet state is favoured compared to the first quartet state at a higher energy. This leads to the advantages of doublet emitters for OLEDs as the formation ratio of the doublet exciton can reach up to 100%. Typical time scales of these processes can be found in Tab. 1.

2.2 Density Functional Theory

Since the DFT/MRCI method uses Kohn-Sham orbitals as a basis, density functional theory plays an important role within the methodological framework.

The origins of DFT reach back to the 1920s. Thomas [103] and Fermi [104] showed that the kinetic energy of atoms and molecules can be approximated via the electron density as a functional of the homogenous electron gas (HEG) instead of using a wave function based approach. This was extended by Dirac [105], who expressed the exchange energy as a functional of the density. This lead to the Thomas-Fermi-Dirac model, where the attraction between the nuclei and the electrons as well as the Coulomb repulsion are

2.2 Density Functional Theory 7

described as functionals of the density [106]. Years later, in the 1950s, Slater [107] proposed mixing WFT with DFT by taking the exchange interaction from Hartree-Fock instead of the functional that was introduced by Dirac. The basis for DFT was founded theoretically by Hohenberg and Kohn in the mid-1960s [108]. The Hohenberg-Kohn theory is exact for systems where the density is nearly constant or slowly varying.

In the simplest form, the DFT Hamiltonian forN non-relativistic, interacting electrons in an arbitrary external potential in atomic units is [108]

Hˆ =−1 2

N

X

i=1

∇²_i +1 2

N

X

i6=j

1

|~r_i−~r_j|+

N

X

i=1

ν(~ri) (1)

where the first summand of Eq. (1) represents the kinetic energy operator T, the second term the electron-electron interactionV_ee and ν(~r) the one-particle external potential.

The ground-state densityρ(r) leads to the number of electrons by integration

N =^Z ρ(~r)d~r (2)

and therefore determines the full Hamiltonian ˆH and all properties determined by ˆH. These include the ground-state wave function Ψ(r1. . . rN), excitation energies and po- tential energy surfaces [109]. The potential ν(~r) is a unique functional of ρ(~r) up to an additive constant. The proof is carried out by reductio ad absurdum. If another po- tential ν⁰(~r) with ground state Ψ⁰ results in the same density ρ(~r), the ground states Ψ and Ψ⁰ lead to different Schrödinger equations. They can therefore not be equal when ν(r)6=ν⁰(r) +const. The ground-state energies and Hamiltonians ofΨ and Ψ⁰ are indic- ated byE andE⁰as well as ˆHand ˆH⁰. The energyE of the ground state can be expressed within the Rayleigh-Ritz principle as

E =^DΨHˆΨ^E<^DΨ⁰HˆΨ^0E=^DΨ⁰Hˆ⁰Ψ^0E−^DΨ⁰H −ˆ Hˆ⁰Ψ^0E

=E⁰+^Z ρ(~r) ν(~r)−ν⁰(~r)dr. (3)

Analogous to Eq. (3), the energyE⁰ of the ground state is

E⁰ =^DΨ⁰Hˆ⁰Ψ^0E<^DΨHˆ⁰Ψ^E=^DΨHˆΨ^E−^DΨHˆ⁰−HˆΨ^E

=E+^Z ρ(~r) ν⁰(~r)−ν(~r)dr. (4)

The energies in Eq. (3) and (4) contradict each other. It follows that the density ρ(~r) determines the potentialν(~r) to within a constant. The energy can therefore be written as a functional of the density as

8 2.2 Density Functional Theory

E_ν(r)[ρ] =^Z ν(~r)ρ(~r)d~r+F[ρ] (5) where the functionalF[ρ] is defined as the sum of kinetic energyT[ρ] and electron-electron interactionVee[ρ],

F[ρ(r)] =

* Ψ

−1 2

N

X

i=1

∇²_i + 1 2

N

X

i6=j

1

|~r_i−~r_j|

Ψ +

. (6)

When the correct densityρ(~r) of a system is known,E_ν(r)[ρ] is the ground-state E [108].

The density that minimises the energy in Eq. (5) corresponds to the ground-state density and leads to the Euler equation

µ=ν(~r) + δF[ρ]

δρ(~r) (7)

with the constraint that the density determines the number of electrons by integration.

Kohn and Sham [110] developed a simplification for the kinetic energy by introducing

Ts[ρ] =

* Ψs

N

X

i=1

−1 2∇²_i

Ψs

+

=

N

X

i=1

ψi

−1 2∇²_i

ψi

. (8)

The new kinetic energy T_s[ρ] restricts the density to be noninteracting ν-representable, i.e. for a given densityρ(~r) there must exist a noninteracting ground state.

By separating the contributions, the functionalF[ρ] in Eq. (6) can be rewritten as

F[ρ] =T_s[ρ] +J[ρ] +E_xc[ρ] (9) with

J[ρ] = 1 2

Z Z ρ(~r)ρ(~r⁰)

|~r−~r⁰| d~r d~r⁰ (10) as the interaction energy. Ts[ρ] represents the kinetic energy of a noninteracting system as above. The third term in Eq. (9) represents the exchange-correlation energy and is defined as

Exc[ρ] =T[ρ]−Ts[ρ] +Vee[ρ]−J[ρ]. (11) The Euler equation in Eq. (7) is now

2.3 Open Shells in Density Functional Theory 9

µ=νef f(~r) +δT_s[ρ]

δρ(~r) . (12)

The Kohn-Sham effective potential can be expressed as

νef f(~r) =ν(~r) +δJ[ρ]

δρ(~r) =ν(~r) +^Z ρ(~r⁰)

|~r−~r⁰|d~r⁰+νxc(~r) (13) with the exchange-correlation potential

νxc(~r) = δE_xc[ρ]

δρ(~r) . (14)

Eq. (12) with the constraint Eq. (2) yields the same equation as non-KS DFT for a system of noninteracting electrons in an external potential ν_s(~r) = ν_{ef f}(~r). Hence, the density for a givenν_{ef f}(~r) is procured by solving [111]

−1

2∇²+ν_{ef f}(~r)ψi =εiψi (15) with

ρ(~r) =

N

X

i=1

|ψ_i(~r)|². (16) Eq. (13)–(16) are the Kohn-Sham equations. Eq. (15) shows that the moving electrons can be considered in the same manner as a system of noninteracting electrons [112]. The electrons are treated as moving in the potential ν_{ef f}(~r), which contains all interactions between the electrons [112].

The energy then is

E =

N

X

i=1

εi−1 2

Z Z ρ(~r)ρ(~r⁰)

|~r−~r⁰| d~r d~r⁰+Exc[ρ]− Z

νxc(~r)ρ(~r)d~r. (17) DFT is widely used for electronic structure calculations due to its practicality and univer- sality [113]. Kohn-Sham DFT is covering the dynamic electron correlation, but the static Coulomb correlation is neglected. Static correlation arises from a strong interaction of electronic states that are degenerate or near-degenerate [106].

2.3 Open Shells in Density Functional Theory

The DFT method as outlined in Sec. 2.2 is applicable to restricted orbitals, i.e. orbitals that are either doubly occupied or vacant, with the same orbital forαandβ spin. In order to construct an anchor configuration for the DFT/MRCI method for doublet and quartet

10 2.3 Open Shells in Density Functional Theory

α β α β α β

RKS ROKS UKS

Figure 2: Differences between closed-shell (RKS), restricted open-shell (ROKS) and unrestricted (UKS) Kohn-Sham orbitals. While the spin of the open shells in ROKS and UKS is arbitrary, an α-spin is conventionally used.

states, or more generally for states with an odd number of electrons, a different orbital basis is required. Several ways of constructing the open-shell determinant come to mind.

The most common variant is to take an unrestricted approach with two unique sets of spin orbitals forα and β electrons. This ansatz requires any post-HF method to employ unrestricted orbitals as well. In this case, unrestricted configuration interaction (UCI) is not built on a good theoretical foundation [114, 115] and the results are unreliable.

A different way is to start from a closed-shell determinant and removing or adding one electron. This will lead to unphysical orbital energies and is not suitable for a method that is directly based on the orbital energy like DFT/MRCI. The third way is a different type of DFT, namely restricted open-shell Kohn-Sham. Here, all doubly occupied orbitals are restricted orbitals in addition to fractionally occupied open shells. The ROKS approach is suited best for the DFT/MRCI method. The UKS approach, while not directly employed within the DFT/MRCI framework, still plays an important role for geometry optimisations and TDDFT calculations in this thesis.

Both UKS and ROKS use a noninteracting reference with two independent subsystems.

In the UKS approach, these are the spinsα and β. In the ROKS approach, on the other hand, these are closed and open shells, which are marked with the indicesc and oin the following. The shells ofα and β electrons are restricted to be identical. The scheme of the differences between restricted and restricted open-shell Kohn-Sham and unrestricted Kohn-Sham is shown in Fig. 2.

2.3.1 Restricted Open-Shell Kohn-Sham Density Functional Theory

The restricted orbital Kohn-Sham method was developed by Filatov and Shaik [116, 117]

in the late 90s. It is based on the work of Roothan [118], who extended the Hartree-Fock method to restricted open shells. The multiplet states are built from linear combinations of determinants ΦL since^hH,ˆ Sˆ²ⁱ= 0 [119]. These have the form

Ψ(r) =^X

L

a_LΦL (18)

In its general form, the multiplet energy is determined as the sum of the energies of

2.3 Open Shells in Density Functional Theory 11

different microstates ΦL, with weightscLthat are fixed by symmetry as

E=^X

L

c_LE(ΦL) , ^X

L

c_L= 1. (19)

The microstates are considered as states of mixed symmetries. In the noninteracting case they can be represented by a single determinant [120]. Restricted open-shell Kohn-Sham shows strong similarities to the restricted open-shell Hartree-Fock method [118], but differs in the construction of the microstates. In the ROHF case, the wave function is averaged over the microstates, whereas in the ROKS case the energy and density are averaged [120].

The determinants ΦLare constructed from the same set ofNcclosed-shell orbitalsψk and N_o open-shell orbitalsψ_m. In the following, k,lrefer to closed shells,m,nto open shells andi,j to a general set of orbitals.

The density of the microstates is analogous to the closed-shell case in Eq. (16) and includes the open shells as

ρ^σ_L(~r) =

Nc

X

k=1

|ψ_k(~r)|²+

Nc+No

X

m=Nc+1

n^σ_m,L|ψ_m(~r)|², σ=α, β (20)

withn^σ_m,L as the integer orbital occupation number.

Similar to the closed-shell RKS case in Eq. (17), the energy can be expressed by summing over orbitals instead of electrons as

E=^X

k

2hk+^X

k,l

2Jkl+^X

m

fm

"

2hm+ 2^X

k

2Jkm+^X

n

2fnamnJmn

#

+^X

L

cLExc,L (21)

which includes an interaction term J_km between closed shells k and open shells m. The one-electron integrals include the kinetic energy and the interaction with the external potential, corresponding to the first and third terms of Eq. (1). The two-electron integrals J_klare the Coulomb integralsJ_kl=hkl|kli. The occupation of themth orbital is given by

f_m = 1 2

X

L

c_Ln^α_m,L+n^β_m,L (22)

and the coupling coefficient is

amn= 1 4fmfn

X

L

cL

n^α_m,L+n^β_m,L n^α_n,L+n^β_n,L. (23)

The exchange-correlation potential from Eq. (14) becomes

12 2.3 Open Shells in Density Functional Theory

νxc(r) = δE_xc,L[ρ]

δρL(~r) (24)

by taking the microstates into account. By summing over the microstates, the exchange- correlation potentials for the sets of closed and open shells are

V_xc^c = 1 2

X

L

c_Lν_xc.L^α +ν_xc,L^β (25) and

V_xc^o = 1 2f

X

L

c_Lν_xc,L^α n^α_m,L+ν_xc,L^β n^β_m,L (26) which includes the occupation of themth open shell.

In order to apply the variational principle to obtain the orbital equations, a new operator for the Coulomb interaction has to be introduced for open shells, as these shells depend on the fractional occupation. The resulting operator describing the total Coulomb interaction of closed-shell and open-shell orbitals is

JˆT =^X

k

Jˆk+f^X

m

Jˆm. (27)

For any orbital ψi, closed-shell, open-shell or virtual, the following eigenvalue equation [116] is obtained

−1

2∇²+ν(~r) + 2 ˆJ_T +V_xc^c +^X

m

ˆγ^h2 ˆJ_o^m+βV_xc^c −V_xc,m^{o i}|ψ_mi hψ_m| +|ψ_mi hψ_m|^h2 ˆJ_o^m+βV_xc^c −V_xc,m^{o i}γˆ

|ψ_ii=ε_i|ψ_ii (28) with the density operators

ˆ ρo =^X

m

|ψ_mi hψ_m| (29)

and

ˆ

γ = ˆρc−(1−f) +1−f

2 ρˆo. (30)

In the case that is relevant for DFT/MRCI, only one half-closed shell, i.e. a singly occupied orbital, is considered. For a singly occupied shell the coupling coefficient is f =¹/2, with

2.3 Open Shells in Density Functional Theory 13

αmn = 0 and β = 2 and the exchange-correlation potential is V_xc,m^o = V_xc,n^o =V_xc^o. This simplifies Eq. (28) to

−1

2∇²+ν(~r) + 2 ˆJ_T +V_xc^c + 2ˆγ(V_xc^c −V_xc^o) ˆρ_o+ 2ˆρ_o(V_xc^c −V_xc^o) ˆγ

|ψ_ii=ε_i|ψ_ii. (31)

Within the ROKS theory, the conventional naming of the highest occupied molecular orbital (HOMO) of closed-shell orbitals is ambiguous, since both the doubly and singly occupied orbitals are occupied and HOMO might refer to both. For this reason the highest doubly occupied molecular orbital is called HDOMO while the singly occupied molecular orbital of a system with a doublet ground state is called SOMO.

2.3.2 Unrestricted Kohn-Sham

The unrestricted Kohn-Sham [121–123] (UKS) orbitals (just as unrestricted Hartree-Fock orbitals) are disadvantageous within the configuration interaction method. The wave function is not an eigenfunction of the ˆS² operator and – due to this property – spin contamination can occur in unrestricted wave functions, caused by differences in the spatial parts of the α and β orbitals [114]. However, UKS still plays an important role in the framework of DFT/MRCI as the DFT/MRCI method depends on optimised geometries of the ground state and/ or excited states. UKS is widely available in quantum chemical programs, including analytical gradients and Hessians for excited states. For optimising the structure of an excited doublet state, UKS is currently the only available option within the time-dependent density functional theory.

The wave function is constructed as a Slater determinant of spin-orbitals. In the unres- tricted formalism, the potential in Eq. (9) has to be rewritten to take the α and β spin densities into account

F^hρ^α, ρ^βi=T_s^hρ^α, ρ^βi+J^hρ^α+ρ^βi+E_xc^hρ^α, ρ^βi. (32) Analogous to the restricted Kohn-Sham orbitals in Eq. (16) and the restricted open-shell orbitals in Eq. (20), the density is

ρ(~r) =

N^α

X

i=1

|ψ_i^α(~r)|²+

N^β

X

i=1

ψ_i^β(~r)

2. (33)

The Kohn-Sham potential, analogous to Eq. (13) of the RKS equations, is given by

ν_{ef f}^σ (~r) =ν(~r) +^Z ρ^α(~r⁰) +ρ^β(~r⁰)

|~r−~r⁰| d~r⁰+ν_xc^σ (~r), σ=α, β (34) with the exchange-correlation potential similar to Eq. (14) of the restricted and Eq. (24)

14 2.4 DFT Functionals

of the restricted open-shell orbitals as

ν_xc^σ = δExc

hρ^α(r)ρ^β(r)ⁱ

δρ^σ(r) , σ=α, β. (35)

Thus, the eigenvalue equation (15) becomes [124]

−1

2∇²+ν_{ef f}^σ (~r)ψ_i^σ =ε^σ_iψ^σ_i, σ=α, β. (36) 2.4 DFT Functionals

In order to apply the DFT method, knowledge of the exchange-correlation energy (see Eq. (9), (21) and (32)) is necessary. But as the exact exchange-correlation energy func- tional is not known, approximate functionals are used. The amount of available exchange- correlation functionals is so large that some authors call it a ‘zoo’ [125]. In the following, the functionals that play a key role in this thesis are introduced. The most important of them is the BHandHLYP functional due to its role within the DFT/MRCI method. Other functionals were used for geometry optimisations and excited state TDDFT reference en- ergies in the context of validating and comparing the performance of DFT/MRCI.

2.4.1 BHandHLYP

The BHandHLYP [126, 127] functional employs a 1:1 mix of Hartree-Fock and the local spin density approximation [108, 110] (LSDA) with the Becke88 [128] correction. The class of functionals that mix exact and DFT exchange is called hybrid functionals. For describing the correlation energy, the LYP correlation by Lee, Yang and Parr [127] is used.

The correlation functional was derived by fitting the density of helium. The exchange- correlation energy in BHandHLYP is

E_xc= 0.5E_x^HF + 0.5E_x^LSDA+ 0.5∆E_x^B88+E_c^{LY P} (37) The Becke88 [128] exchange is a correction to the LSDA exchange.

2.4.2 B3LYP

The B3LYP functional is used for geometry optimisations in the purely organic vertical excitation training (fitting) and testing sets of the R2017 parameter set (Paper 1). This set is also employed for the R2018 Hamiltonian (Paper 2). The set of molecules can be found in Sec. 3.

The B3LYP functional employs exchange interaction from Hartree-Fock and LSDA with the Becke88 correction in combination with LYP and Vosko, Wilk, and Nusair [129] (VWN) correlation. The exchange-correlation energy is obtained by

2.5 Configuration Interaction and Electron Correlation 15

Exc= 0.2E_x^HF + 0.8E_x^LSDA+ 0.72∆E_x^B88+ 0.81E_c^{LY P} + 0.19E^{V W N}_c (38)

2.4.3 PBE0

The PBE0 [130] functional, also known as PBE1PBE or PBE hybrid, is the hybrid version of the pure Perdew, Burke, and Ernzerhof (PBE) [131, 132] functional. The exchange is de- scribed by a 1:3 mix of exact to PBE exchange. The PBE0 functional is used for geometry optimisations of transition metal complexes in Paper 2 [133] and Paper 4 [134], for the optimisation of the Blatter radical in Paper 3 [67] and for the PAH-DTDA, TARA-PCTM and TTM-1Cz radicals in Sec. 6. The functional is based on the PBE exchange correl- ation. The exact exchange is introduced by substituting 25% of the the PBE exchange with exact exchange as

Exc=E_xc^{P BE}+1 4

E_x^HF −E_x^{P BE} (39)

2.4.4 MN15

The MN15 [135, 136] functional is a new functional developed for a broader range of applic- ations [135]. The functional is based on a non-separable gradient approximation (NGA) of type global-hybrid meta-NGA and improves the accuracy of systems with multicon- figurational character. For this reason, it was employed in Paper 5 [137] for optimising the ground state and the multiconfigurational excited states D1 and D3. The exchange- correlation energy is

E_xc= 0.44E_x^HF +E_nxc^{M N15}+E_c^{M N15} (40) withE_nxc as the non-separable local exchange-correlation energy [135].

2.5 Configuration Interaction and Electron Correlation

Multireference configuration interaction (MRCI) is – next to density functional theory – the second part of the DFT/MRCI method. The anchor configuration is constructed from a DFT basis and the calculation of matrix elements is carried out in a truncated CI scheme.

Configuration interaction is a post-Hartree-Fock method that dates back to the late 1920s [138]. It introduces the electron correlation missing in the mean-field approach of Hartree and Fock [139]. Correlation energy is defined as the difference between the exact energy and the energy obtained within the Hartree-Fock theory in a complete basis set, the HF limit [140]. The correlation energy describes only a small part of the total energy, e.g. 0.5% in case of H2O. But the bond energy is about the same amount and thus small energy contributions can lead to large effects [141]. Correlation can be divided