424 10. Differenzialrechnung bei Funktionen mit mehreren Variablen
10.4
10.4 Anwendungen der Differenzialrechnung
Wir werden in diesem Abschnitt einige wichtige Anwendungen der Taylorschen Formel behandeln: Das totale Differenzial als lineare N¨aherung, die Fehlerrechnung, die Theorie der Maxima und Minima bei Funktionen von zwei Variablen sowie die Bestimmung von Ausgleichungsfunktionen insbesondere der Regressionsgeraden.
Hinweis:Alle Themen werden durchMaple-Prozeduren erg¨anzt, die sich zus¨atzlich auf der Homepage befinden.
10.4.1 Das Differenzial als lineare N¨aherung
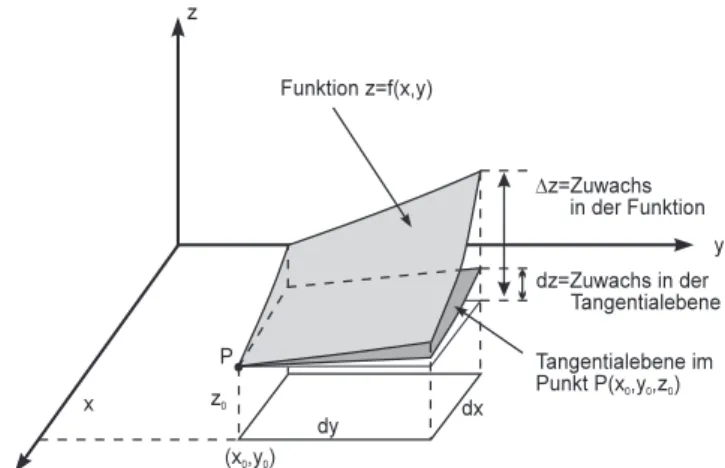
Wir untersuchen das Verhalten der Funktion z = f(x, y) in unmittelbarer Umgebung des Punktes(x0, y0), indem wir den Zuwachs der Tangentialebene dzmit dem Zuwachs der Funktion∆z vergleichen.
Abb. 10.21.Zum Begriff des vollst¨andigen Differenzials
Die Tangentialebene der Funktion z = f(x, y) ist im Punkte (x0, y0) nach Abschnitt 10.3.2 bestimmt durch
zt(x, y) =f(x0, y0) + (x−x0)fx(x0, y0) + (y−y0)fy(x0, y0) . Im Punkte(x0+dx, y0+dy)hat die Tangentialebene den Wert
zt(x0+dx, y0+dy) =f(x0, y0) +dx fx(x0, y0) +dy fy(x0, y0) . Die ¨Anderung der Tangentialebenedzist daher
dz=zt(x0+dx, y0+dy)−zt(x0, y0) = dx fx(x0, y0) +dy fy(x0, y0) . Wir bezeichnen
dx, dy: unabh¨angiges Differenzial
dz: abh¨angiges Differenzial(= ¨Anderung der Tangentialebene) und definieren
10.4 Anwendungen der Differenzialrechnung 425
Definition: (Totales Differenzial einer Funktion mit zwei Varia- blen).Das totale Differenzialeiner Funktion z =f(x, y) im Punkte (x0, y0)ist
dz:=fx(x0, y0)dx+fy(x0, y0)dy.
Es beschreibt die ¨Anderung der Tangentialebene im Punkte(x0, y0),wenn man vom Punkt (x0, y0) zum Punkt (x0+dx, y0+dy)ubergeht.¨ Statt dz schreibt man auchdf.
Beispiel 10.23.Gesucht ist das totale Differenzial der Funktion f(x, y) =xln (x+y)
im Punkte(x0, y0) = 12, 12 .
∂f
∂x = ln (x+y) +x· 1 x+y
∂f
∂y =x· 1 x+y
df=
ln (x+y) + x x+y
dx+ x x+ydy .
⇒df(x0, y0) = 1 2dx+1
2dy.
Wir vergleichen dieAnderung der Tangentialebene¨ dzmit derAnderung¨ der Funktion4z, indem wir f¨ur die Funktionz=f(x, y)linearisieren, d.h.
die Taylorsche Formel f¨urn= 1 verwenden:
f(x, y)−f(x0, y0) = (x−x0)fx(x0, y0) + (y−y0)fy(x0, y0) +R1(x, y). Die ¨Anderung der Funktion4zvon(x0, y0)nach(x0+dx, y0+dy)ist
4z = f(x, y)−f(x0, y0) =f(x0+dx, y0+dy)−f(x0, y0)
= dx fx(x0, y0) +dy fy(x0, y0) +R1(x0+dx, y0+dy)
= dz+R1(x0+dx, y0+dy).
Sie stimmt mit der ¨Anderung der Tangentialebenedz dz=dx fx(x0, y0) +dy fy(x0, y0)
bis auf den Term R1(x0+dx, y0+dy) ¨uberein. F¨ur (dx, dy) → (0,0) geht R1(x0+dx, y0+dy)→R1(x0, y0) = 0, so dass f¨ur kleinedx, dygilt
dz≈ 4z.
426 10. Differenzialrechnung bei Funktionen mit mehreren Variablen
Totales Differenzial von Funktionen mitn Variablen
Der Begriff des totalen Differenzials ¨ubertr¨agt sich direkt auf Funktionen mit mehr als zwei Variablen:
Definition: (Totales Differenzial einer Funktion mitnVariablen).
Unter demtotalen Differenzial einer Funktion
y=f(x1, . . . , xn) versteht man den Differenzialausdruck
dy := fx1dx1+fx2dx2+. . .+fxndxn
= ∂f
∂x1
dx1+ ∂f
∂x2
dx2+. . .+ ∂f
∂xn
dxn.
Bemerkungen:
(1) Stattdyschreibt man auch df.
(2) Das totale Differenzial beschreibt n¨aherungsweise, wie sich der Funktions- wert ¨andert, wenn sich die Variablen geringf¨ugig um dxi (i= 1, . . . , n)
¨andern:4y≈dy.
Beispiele 10.24.
1 Gesucht ist das totale Differenzial der Funktion f(x, y, z) =x ex y+4z im Punkte (x0, y0, z0) = (1,0,1):
∂f
∂x =ex y+4z+x ex y+4zy ,→fx(1,0,1) =e4
∂f
∂y =x2ex y+4z ,→fy(1,0, 1) =e4
∂f
∂z = 4x ex y+4z ,→fz(1,0,1) = 4e4. Mit der Formel des totalen Differenzials
df=fxdx+fydy+fzdz erhalten wir f¨urdf
df(x, y, z) = ex y+4z+x y ex y+4z
dx+x2ex y+4zdy+ 4x ex y+4zdz df(1,0,1) =e4dx+e4dy+ 4e4dz.