Massively Parallel Algorithms

(1)

Massively Parallel Algorithms

Dense Matrix Algorithms

G. Zachmann

University of Bremen, Germany cgvr.cs.uni-bremen.de

(2)

G. Zachmann Massively Parallel Algorithms SS 17 September 2020 Matrix Algorithms 3

Warming Up: Matrix-Vector Product

§ Given matrix A, and vector x, compute

§ One of the most important operations in linear algebra algorithms

§ Called SGEMV in BLAS (Basic Linear Algebra Subroutines)

§ First approach: one thread per row

§ Observation: all threads use the same data from x → shared memory

y = Ax

= *

y[i]

A[i,*]

x[]

N

M

(3)

§ For sake of clarity, we assume M, N= multiple of block-size

multMatrixVector( const float * A, const float * x, const int n_columns, float * y )

{

__shared__ x_cache[ THREADS_PER_BLOCK ];

float yi = 0.0; // output of each thread int i = threadIdx.x + blockIdx.x * blockDim.x; // row index for ( int j = 0; j < n_columns; j += THREADS_PER_BLOCK )

{

// new segment of columns → fill cache

x_cache[threadIdx.x] = x[ j + threadIdx.x ];

// now process this segment of columns

for ( int k = 0; k < THREADS_PER_BLOCK; k ++ )

{

Aij = A[ i*n_columns + j+k ];

yi += Aij*x_cache[k];

} }

y[i] = yi;

}

Algorithm for First Attempt (One Thread per Row)

i *

j

Block of threads

Blocksize

Block- size

(4)

§ The "natural way" (the "C way") to store matrices is called row major order

§ A_ij is stored at memory address A + i*n_cols + j

§ For a conventional (sequential)

matrix-vector-multiplication algorithm, this is good:

0 4 8 12 16

1 5 9 13 17

2 6 10 14 18

3 7 11 15 19

cachelines for ( int i = 0; i < n_rows; i ++ )

{

float yi = 0.0;

for ( int j = 0; j < n_cols; j ++ ) yi += A[i][j] * x[j];

y[i] = yi;

}

(5)

Coalesced Memory Access

§ One of the most important optimization techniques for massively parallel algorithm design on GPUs and — to some degree — CPUs!

Coalesced memory accesses Uncoalesced memory accesses

Aligned and sequential memory

access (a few gaps are OK) Aligned but not sequential

Sequential but not aligned

(6)

2D Array Access Patterns (row major vs column major)

§ Consider the following piece in a kernel (e.g., matrix × vector):

§ Generally, most natural access pattern for direct port of C/C++ code

ØProblem: uncoalesced access pattern

§ Elements read on 1^st SIMT access: 0, 32, 64, …

§ Elements read on 2^nd SIMT access: 1, 33, 65, …

§ Also, extra data will be transferred in order to fill the cache line size for ( int j = 0; j < blockDim.x; j ++ ) {

float Aij = A[treadIdx.x][j];

... do something with it ...

Memory layout of a matrix in C

= row major order

float A[N][32];

...

Aij = A[treadIdx.x][0];

Aij = A[treadIdx.x][1];

...

1 thread per row

(7)

How to Achieve Coalesced Access

§ Addresses from a warp (“thread-vector”) are converted into memory line requests

§ Line sizes: 32B (= 32x char) and 128B (= 32x float)

§ Goal is to maximally utilize the bytes in these lines

§ GPU wins over CPU at memory access, if it is "streamed" = coalesced

§ Hence, "stream programming architecture"

Read/write bandwidth

10³ 10⁴ 10⁵ 10⁶ 10⁷ 10⁸ Array size

Speed (GB/s)

(8)

for ( int j = 0; j < blockDim.x; j ++ ){

float Aij = A[treadIdx.x][j];

Column Major (Transposed) 2D Array Access Pattern

§ Column major := store a logical row in a physical column

§ I.e., A₀₀ → A[0][0] , A01 → A[1][0] , A02 → A[2][0] , … A₁₀ → A[0][1] , A₁₁ → A[1][1] , A₁₂ → A[2][1] , … A₂₀ → A[0][2] , …

§ In general: A_ij is stored at A + j*n_columns + i

§ Transform the code to column major:

§ Now, we have coalesced accesses:

§ Elements read on 1^st SIMT access: 0, 1, 2, …, 31

§ Elements read on 2^nd SIMT access: 32, …, 63

0 1 2 3 4

5 6 7 8 9

10 11 12 13 14

15 16 17 18 19

float A[32][N];

...

Aij = A[0][treadIdx.x];

Aij = A[1][treadIdx.x];

... 1 thread per logical row =

1 thread per physical column

for ( int j = 0; j < blockDim.x; j ++ ){

float Aij = A[j][treadIdx.x];

(9)

Array of Struct's or Struct of Arrays?

§ An array of structs (AoS) yields memory accesses like row major:

§ A struct of arrays (SoA) yields memory accesses like column major:

struct Point { float x, y, z;

};

Point PointList[N];

...

PointList[threadIdx].x = ...

struct PointList { float x[N];

float y[N];

float z[N];

};

...

PointList.x[threadIdx] = ...

(10)

multMatrixVector( const float * A, const float * x, const int n_columns, float * y )

{

float yi = 0.0; // output of each thread int i = threadIdx.x + blockIdx.x * blockDim.x; // row index for ( int j = 0; j < n_columns; j += THREADS_PER_BLOCK )

{

Aij = A[ i*n_columns + j+k ];

yi += Aij * x_cache[k];

} }

y[i] = yi;

}

multMatrixVector( const float * A, const float * x, const int n_??????? , float * y )

{

float yi = 0.0; // output of each thread int i = threadIdx.x + blockIdx.x * blockDim.x; // row index for ( int j = 0; j < n_columns; j += THREADS_PER_BLOCK )

{

Aij = A[ i + (j+k)*n_??????? ];

yi += Aij * x_cache[k];

} }

y[i] = yi;

}

Modified Matrix*Vector Algorithm for Column-Major Matrix Storage

n_columns n_columns

Note: n_columnsis still the

number of columns of the logicalmatrix,

notthe number of columns of the physicalmatrix!

(11)

§ Note: from now on, we will use row-major notation (just for sake of clarity)!

§ But we will assume that an actual implementation uses column-major!

§ We expect you to transform everything to column-major

§ Start with small matrices that you can check "by hand"

§ Or implement your code first on the CPU and test it there

(12)

Auto-Tuning

§ Do we keep all hardware resources of the GPU busy?

§ On Fermi [2011] hardware (for instance):

§ 14 SMs, each supports 1536 active threads

§ If N < 14×1536 = 21504 → some SMs are idle!

§ Idea for the case N < 21504 and M "not too small":

§ Use 2D partitioning of our problem/domain

*

N

M Block 0,0 Block 0,1

Block 1,0 Block of

threads

Cache size

Cache size segments of a row that will be multiplied to x_cache

segments of x that will be stored in x_cache

(13)

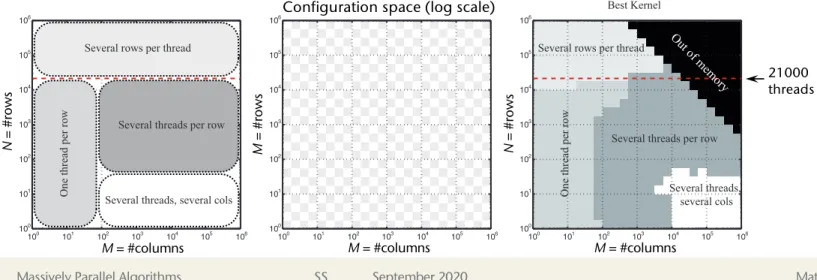
§ All possible domain decomposition variants:

1. One thread per row

2. Several threads per row (previous slide)

3. Several rows per thread (one thread computes several y[i]'s at the same time) 4. Several threads per row, each thread handles several rows (2 & 3)

§ Which version is best in which case? (YMMV)

High-Performance Matrix-Vector Multiplication on the GPU 3

10⁰ 10¹ 10² 10³ 10⁴ 10⁵ 10⁶

One thread per row

Several rows per thread

Several threads per row

Several threads, several cols m

n

10⁰ 10¹ 10² 10³ 10⁴ 10⁵ 10⁶

m

n Logarithmic mesh

10⁰ 10¹ 10² 10³ 10⁴ 10⁵ 10⁶

One thread per row

Several rows per thread

Several threads per row

Several threads, several cols m

n Best Kernel

Out of m emory

Fig. 1. Left; Four matrix-vector multiplication kernels designed to perform well at di↵erent shapes m⇥n of A. Middle; Tuning mesh. Right; Best kernel in practice. The dashed line indicates the minimum 21504 rows needed in A for full occupancy of the Nvidia Tesla C2050 card in a one-thread-per-row kernel. Note the logarithmic axes.

row of A and x to produce one element of the result y. The threads are then grouped in 1D blocks along the columns of A. For a given size of A, the only parameter required is the number of threads per block, which we will denote by BLOCKSIZE. The size of the grid specified when launching the kernel in CUDA is determined by the BLOCKSIZE parameter. Dividing the m rows of A into slices of size BLOCKSIZE, with the last slice possibly containing less than BLOCKSIZE rows, we have a one dimensional grid of size

GRIDSIZE m = (m+BLOCKSIZE 1)/BLOCKSIZE.

Using a grid of this size requires an if conditional inside the kernel to make sure the last block does not access memory outside the m rows of A. In Fig. 2 (a) the kernel is shown for a GRIDSIZE m of 4 as indicated with the red 4⇥1 mesh.

Since all threads need the same n values of x for their dot products it is best to read these into shared memory once per block and then let threads access them from there. This allows for maximum reuse of the data. We therefore divide x into chunks of BLOCKSIZE and set up a loop to let the threads collaborate in reading chunks in a coalesced fashion into a shared memory once per block. It requires the allocation of a shared memory array of size BLOCKSIZE for each block. The usage of shared memory is illustrated by red-dotted boxes in Fig. 2.

The one-thread-per-row matrix-vector multiplication kernel is appropriate as a high-performance kernel on the C2050 card for tall and skinny A only. This is because the Fermi GPU with 14 SMs supports 1536 active threads per SM [10], so that full occupancy requires 1536⇥14 = 21504 rows in A. If mis less than this, and A is not skinny, then we are not utilizing the hardware to the maximum.

SMs might be idle or running at low occupancy during kernel execution, while the running threads might do a lot of work each. If A is skinny, e.g., n < 100, then dispite the low utilization, the individual threads complete fast enough for this kernel to be the best implementation. In Fig. 1, we indicate the dimensions of A for which the one-thread-per-row kernel is designed to perform well.

21000 threads

M= #columns M= #columns M= #columns

N= #rows

M= #rows

N= #rows

Configuration space (log scale)

(14)

§ Computational performance that can be achieved [2011]:

Fast High-performance Modeling Tools for Many-core Architectures

Stefan L. Glimberg, Allan P. Engsig-Karup, Hans Henrik B. Sørensen, Nicolai F. Gade-Nielsen, Dennis Noer, Erik Zenner, Morten G. Madsen

Introduction and Background

GPULab - A competence center and laboratory for research and collaboration within academia and partners in the industry. Established in 2008 at the Section for Scientific Computing, DTU Informatics, Technical University of Denmark. In GPULab we focus on the utilization of Graphics Processing Units (GPUs) for high-performance computing applications and software tools in science and engineering. The goals are to contribute to the development of new state-of-the-art mathematical models and algorithms for maximum performance and assimilation of results to academic and industrial partners in our network. Our approaches calls for multi-disciplinary skills and understanding of hardware, software development, profiling tools and tuning techniques, numerical analysis, along with expert knowledge application areas within science and engineering.

Per Christian Hansen Jan Hesthaven

Bernd Dammann

John Bagterp Jørgensen

Allan Engsig-Karup Jeppe Frisvad

Boyan Lazarov

Hans Henrik Brandenborg Sørensen

Stefan Lemvig Glimberg Nicolai Fog Gade-Nielsen http://gpulab.imm.dtu.dk/

Development of a Massively Parallel Wave Analysis Tool

Ongoing work is concerned with the development of a GPU-accelerated nonlinear free-surface model (OceanWave3D) for simulation of unsteady fully nonlinear water waves over uneven depths. The flexible-order finite difference model is based on a unified potential flow formulation, under the assumption of irrotational inviscid flow. We have redesigned the entire algorithm to enable efficient utilization of allocated hardware resources - currently targeting many-core GPUs.

Algorithmic efficiency is achieved by solving the bottleneck problem, a large sparse linear system of equations, iteratively by employing a defect correction method preconditioned by a robust multigrid method. This strategy results in more than an order magnitude in both problem size and practical speedup (relative to optimized single-threaded CPU code).

GPULab Library – a High-performance GPU-based Library for the Development of Scientific Applications

We have an ongoing development of a GPU-based generic C++ library for scientific computing. The two main goals are to create a common playground for the developers at the section and interested network contacts, and to keep an up-to-date platform containing the latest results from the developers. We now have several components for solving large scale partial differential equations.

However, this should not be a limitation and we soon expect to have show-cases with dynamic optimization and model control problems as well. In the future we seek to expand the library into a fully distributed tool, in order to achieve maximum performance on cluster-based hardware systems.

Fast Cryptanalysis Tool

In this project the focus has been on developing an efficient high-performance tool for crypto-analysis, utilizing affordable many-core consumer Graphics Processing Units (GPUs). The crypto-analysis is based on a bit- sliced DES brute force algorithm. We are developing an efficient implementation of the DES algorithm, which relies mostly on bitwise operations and takes advantage of the high on-chip bandwidth of GPUs. The current implementation is based on CUDA and a GTX 275 gaming card. A break down of the step-wise improvement in the model demonstrates ~10 times speed up in the initial naïve implementation, and after a range of incremental optimizations the implementation achieved a speed up of ~20 times. With the GTX 275 we have found that it is possible to test up to 680 million password keys per second, which is a significant improvement.

Fig. 1:We achieve linear scaling of the memory footprint for an increasing number of total grid points.

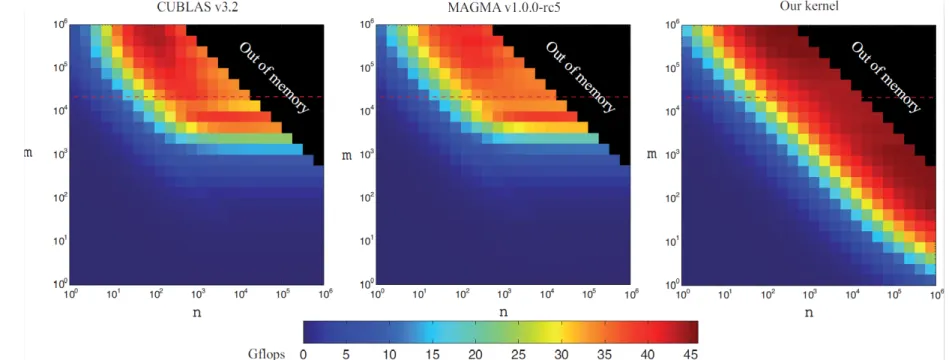
Auto-tuning of Dense Linear Algebra on GPUs

We have implemented an auto-tuning framework that can automate the performance tuning process by running a large set of empirical evaluations to configure applications and libraries on the targeted GPU platform. Preliminary work is focused on dense vector and matrix- vector operations, which form the backbone of level 1 and level 2 routines in the Basic Linear Algebra Subroutines (BLAS) library and are therefore of great importance in many scientific applications. As an example, we develop a single-precision CUDA kernel for the matrix- vector multiplication (SGEMV). The target hardware is the most recent Nvidia Tesla 20-series (Fermi architecture). Our tuned kernels display significantly better performance than the current CUBLAS v.3.2 library.

Fig. 3: Performance of matrix-vector multiplication (SGEMV) in color coded form over the 24x24 logarithmic auto-tuning mesh of matrix sizes. Dark blue represents low performance, while dark red represent high performance. The figures compare our auto- tuned kernel to the most commonly used numerical libraries for GPUs, the Nvidia CUBLAS v3.2 and the MAGMA v1.0.0-rc5.

Accelerating Economic Model Predictive Control using GPUs

As stochastic energy production such as wind becomes more common, it is necessary to either store the energy for later consumption or control the energy consumption to coincide with the energy production. One method to address this problem is the Smart Grid, where Model Predictive Control can be used to optimize energy consumption to match with the predicted stochastic energy production and minimize the cost of energy production from conventional power plants. This can be formulated as a convex optimization problem and solved using primal-dual interior-points methods. The main computational tasks in such a method are matrix-matrix multiplications and Cholesky factorization, both of which are very suitable for GPU acceleration. Initial results of a test case controlling two power plants to match energy consumption show an speed-up of up to ~25 using a Nvidia Tesla C2050 compared to a sequential CPU version running on a Intel i7-920.

gpulab@imm.dtu.dk – http://gpulab.imm.dtu.dk/

Fig. 5: Power plant control to minimize the energy production cost with a 500 time-step prediction horizon. P.G. #1 is a slow, but cheap power plant while P.G. #2 is a fast, but expensive power plant.

Fig. 4:Efficiency comparison of password key tests per second for CPU, naïve and optimized GPU kernels.

Fig. 2:Performance speedups for several different GPU architectures versus the CPU (single thread) version.

Performance of matrix-vector multiplication (SGEMV) over matrices of size n×m

["Fast High-performance Modeling Tools for Many-core Architectures ", Glimberg et al., 2011]

(15)

Arithmetic Intensity

§ Arithmetic intensity of an algorithm :=

§ Sometimes also called computational intensity

§ Unfortunately, many (most?) algorithms have a low arithmetic intensity → they are bandwidth limited

number of arithmetic operations amount of transferred bytes

(16)

Complexities of Matrix-Vector Multiplication

§ Sequential version: O(n²) (assuming n=m)

§ Parallel version: O(n) parallel time

§ Assuming n parallel threads, one thread per row

§ Arithmetic intensity:

§ Assume following simplified (sequential) version:

§ Number of slow memory references = f = 2n + n²

§ Number of arithmetic operations = o = 2n²

§ Arithmetic intensity → memory bandwidth limited load vector x completely into fast memory for i = 1 ... n: // assuming n = m

load row i of A into fast memory for j = 1 ... m:

yi += A[i][j] * x[j]

store yi in y[i]

a = ^o_f ⇡ 2

(17)

Matrix-Matrix Multiplication

§ Called SGEMM in BLAS

§ Given matrices A and B, compute P = A^.B

§ For sake of simplicity, we'll assume A and B are square matrices of size n×n

§ Sequential algorithm:

21

A

B

P

n n

for i = 1 ... n:

for j = 1 ... n:

s = 0.0

for k = 1 ... n:

s += A[i][k] * B[k][j]

P[i][j] = s

k i

k

j

(18)

§ Complexity: O(n³)

§ Even worse than matrix-vector multiplication!

§ Problem: no data re-use!

§ Theorem (w/o proof):

For all iterative (= non-recursive) matrix-matrix multiplication algorithms, the upper bound on arithmetic intensity is

a = 2n³

2n³ + n² ⇡ 1

ˆa = 2n³

3n² 2 O n

(19)

§ Approach:

§ Use matrix-vector-multiplication idea

§ Run one thread per row of A:

§ Not much better L

for j = 1 ... n:

read column j of B into fast memory (B_cache) foreach i = 1 ... n run one thread in parallel:

s = 0.0

for k = 1 ... n:

s += A[i][k] * B_cache[k]

P[i][j] = s

Naïve Parallel Matrix Multiplication

A

B

a = 2n³

n³ + 2n² ⇡ 2

(20)

Blocked (Tiled) Matrix Multiplication

§ Remember linear algebra class: the procedure

works also for sub-blocks of the matrices

where

are block matrices of size m

§ Assumption: n = multiple of m

§ In production code, you'd have to cope with any matrix size!

- Lots of nitty-gritty details …

A

B

Pij

Aik

Bkj

p_ij = Xn k=1

a_ikb_kj

Pij =

n/m

X

k=1

AikBkj

= A<latexit sha1_base64="9NZVCc3c5N1Ww3smdOoFZdN46ng=">AAACbnicZVHLbhMxFL0ZXiW8UpDYIIQhQipSG810AxukUDYsAyJtpU4YOZ47rRvbM7KvgciaLT/A17BDsOEX+As+ASdpJUKvZPno3MfxPZ42SjpK09+d5NLlK1evbVzv3rh56/ad3ubdfVd7K3AsalXbwyl3qKTBMUlSeNhY5Hqq8GA6e73IH3xE62Rt3tO8wYnmx0ZWUnCKVNHbeVUEOWvZNtsrwuy03WajSJy2jOXSsPzdh6BZTlKjY7rtFr1+OkiXwS6C7Az0h4+//PoOAKNis/MsL2vhNRoSijt3lO02NAnckhQK227uHTZczPgxhuU2LXsaqZJVtY3HEFuya3V6rjmdxMLF5f5NHXmqXkyCNI0nNGI1q/KKUc0W27NSWhSk5owLEZ/kOUUpccItFxRdWpNx3LiVUH4Ou7lFg59ErTU3ZcgrrqWal1hxr6gNuavO8fok6Y2kz5F00iH5JjRod3RdInvJqoV2/Is2mpv9b+VFsL87yNJB9jbrD/dgFRvwAJ7AFmTwHIbwBkYwBgFf4Rv8gJ+dP8n95GHyaFWadM567sFaJFt/AUO6wH0=</latexit><latexit sha1_base64="7uY8Xsc8R1F8U2o3jjEvDEzpa4U=">AAACbnicZVHLbhMxFHWmPEp4NKUSG4QwREhFaqOZboAFUigblgGRNlIdRo7nTuvG9ozs60JkzbY/wK+wYQsbfoG/4BNwklYi9EqWj859HN/jSa2kwzT93UrWrl2/cXP9Vvv2nbv3Njqb9w9c5a2AoahUZUcT7kBJA0OUqGBUW+B6ouBwMn07zx+egXWyMh9xVsNY82MjSyk4Rirv7L7Jg5w2dIfu52F62uzQQSROG0qZNJR9+BQ0ZSg1OKqbdt7ppr10EfQqyC5At//k/Ne3V6POIN9sPWdFJbwGg0Jx546yvRrHgVuUQkHTZt5BzcWUH0NYbNPQZ5EqaFnZeAzSBbtSp2ea40ksnF/u39SRx/LlOEhTewQjlrNKryhWdL49LaQFgWpGuRDxSZ5jlBIn3HKB0aUVGceNWwqxS9hmFgx8FpXW3BSBlVxLNSug5F5hE5grL/HqJOmNxC+RdNIB+jrUYHd1VQB9Tcu5dvyLJpqb/W/lVXCw18vSXvY+6/b3yTLWyUPylGyTjLwgffKODMiQCPKVfCc/yM/Wn+RB8ih5vCxNWhc9W2Qlku2/PiDBEg==</latexit><latexit sha1_base64="7uY8Xsc8R1F8U2o3jjEvDEzpa4U=">AAACbnicZVHLbhMxFHWmPEp4NKUSG4QwREhFaqOZboAFUigblgGRNlIdRo7nTuvG9ozs60JkzbY/wK+wYQsbfoG/4BNwklYi9EqWj859HN/jSa2kwzT93UrWrl2/cXP9Vvv2nbv3Njqb9w9c5a2AoahUZUcT7kBJA0OUqGBUW+B6ouBwMn07zx+egXWyMh9xVsNY82MjSyk4Rirv7L7Jg5w2dIfu52F62uzQQSROG0qZNJR9+BQ0ZSg1OKqbdt7ppr10EfQqyC5At//k/Ne3V6POIN9sPWdFJbwGg0Jx546yvRrHgVuUQkHTZt5BzcWUH0NYbNPQZ5EqaFnZeAzSBbtSp2ea40ksnF/u39SRx/LlOEhTewQjlrNKryhWdL49LaQFgWpGuRDxSZ5jlBIn3HKB0aUVGceNWwqxS9hmFgx8FpXW3BSBlVxLNSug5F5hE5grL/HqJOmNxC+RdNIB+jrUYHd1VQB9Tcu5dvyLJpqb/W/lVXCw18vSXvY+6/b3yTLWyUPylGyTjLwgffKODMiQCPKVfCc/yM/Wn+RB8ih5vCxNWhc9W2Qlku2/PiDBEg==</latexit><latexit sha1_base64="7uY8Xsc8R1F8U2o3jjEvDEzpa4U=">AAACbnicZVHLbhMxFHWmPEp4NKUSG4QwREhFaqOZboAFUigblgGRNlIdRo7nTuvG9ozs60JkzbY/wK+wYQsbfoG/4BNwklYi9EqWj859HN/jSa2kwzT93UrWrl2/cXP9Vvv2nbv3Njqb9w9c5a2AoahUZUcT7kBJA0OUqGBUW+B6ouBwMn07zx+egXWyMh9xVsNY82MjSyk4Rirv7L7Jg5w2dIfu52F62uzQQSROG0qZNJR9+BQ0ZSg1OKqbdt7ppr10EfQqyC5At//k/Ne3V6POIN9sPWdFJbwGg0Jx546yvRrHgVuUQkHTZt5BzcWUH0NYbNPQZ5EqaFnZeAzSBbtSp2ea40ksnF/u39SRx/LlOEhTewQjlrNKryhWdL49LaQFgWpGuRDxSZ5jlBIn3HKB0aUVGceNWwqxS9hmFgx8FpXW3BSBlVxLNSug5F5hE5grL/HqJOmNxC+RdNIB+jrUYHd1VQB9Tcu5dvyLJpqb/W/lVXCw18vSXvY+6/b3yTLWyUPylGyTjLwgffKODMiQCPKVfCc/yM/Wn+RB8ih5vCxNWhc9W2Qlku2/PiDBEg==</latexit><latexit sha1_base64="EioU78sPqCEp/YaDawo+RiKWRA8=">AAACbnicZVHLbhMxFHWmPEp4pUVigxAWEVKR2mimG9hUKmXDMiDSVqrDyPHcad34MbKvoZE1X8HXsIWv4C/4BJxHJUKvZPno3MfxPZ40SnrM89+dbOPW7Tt3N+917z94+Ohxb2v72NvgBIyEVdadTrgHJQ2MUKKC08YB1xMFJ5Pp+3n+5Cs4L635jLMGxpqfG1lLwTFRZW/vXRnltKW79KiM08t2lw4TcdlSyqSh7NOXqClDqcFT3XbLXj8f5IugN0GxAn2yimG51XnNKiuCBoNCce/Piv0Gx5E7lEJB22XBQ8PFlJ9DXGzT0leJqmhtXToG6YJdq9MzzfEiFc4v/2/qLGD9dhylaQKCEctZdVAULZ1vTyvpQKCaUS5EelLgmKTEBXdcYHJpTcZz45dC7Bp2mQMD34TVmpsqspprqWYV1DwobCPz9TVenySDkXiVSC89YGhiA25P2wroAa3n2ukv2mRu8b+VN8Hx/qDIB8XHon94tLJ5kzwjL8kOKcgbckg+kCEZEUG+kx/kJ/nV+ZM9zZ5nL5alWWfV84SsRbbzFyT3vg4=</latexit> _ik,B_kj,P_ij 2 R^m^⇥^m

(21)

§ New approach

§ For each sub-matrix P_ij, run one block of m²threads

§ Each thread in the block computes one p_ij

§ The kernel runs in phases

§ Each phase consists of:

1. Load blocks A_ik, B_kj into shared memory

- Each thread loads one aij, one bij

2. Perform "row × column" over block

3. Accumulate partial results

m

Copy blocks into fast memory

(2D partitioning):

Aik

Bkj

Pij

+

(22)

§ Pseudo code:

let b = n/m // = number of blocks in each dimension foreach i = 1...b, j = 1...b run one block in parallel:

let p = 0.0 // = thread-local accumulator for k = 1 ... b:

load sub-matrices A(i,k) and B(k,j) into shared memory

⟶ Asub , Bsub for l = 1...m:

p += Asub[tid.x][l] * Bsub[l][tid.y]

P[I,J] = p // I,J = per-thread global indices into P

dim3 threadsPerBlock(m,m);

dim3 n_blocks( n/m, n/m ); // # blocks in P (and in A, B) multMatrices<<< n_blocks, threadsPerBlock >>>( A, B, P, n );

Actual kernel!

(23)

§ Previous optimization is called blocking/tiling (copy optimization)

§ How should matrices A and B be stored?

§ Remember: at the beginning of each phase: each thread loads one a_ij &

one b_ij

§ Store matrices in blocked form, in order to achieve coalesced memory access:

0 1 2 3

4 5 6 7

8 9 10 11

12 13 14 15 Original matrix

(numbers are addresses)

0 1 4 5

2 3 6 7

8 9 12 13

10 11 14 15 Reorganized into blocks

(24)

§ P consists of b²blocks

§ For each block P_ij, we load b blocks of A and b blocks of B

§ Overall, our algorithm loads 2b³many blocks

§ One block load = m² float loads

§

§ Overall, our algorithm loads many floats

§ Therefore,

§ Consequence: make m large

§ Bound on m: all three blocks P_ij, A_ik, B_kj, must fit in shared memory b = _mⁿ

2 _mⁿ ³ m² = 2ⁿ_m³ a = 2n³

2ⁿ_m³ = m

(25)

§ Calculating m:

§ Assume Kepler-GPU: ~ 2 TFlops/sec = 2^.10¹²Flops/sec ,

~ 200 GB/sec = 200^.10⁹ B/sec

§ Choose m such that we achieve peak bandwidth & peak Flops/sec

§ m = a =

§ Note: these are very crude estimations, but good for a starting point where to search for the sweet spot

§ Consequence: size of shared memory should be at least 3 ^. 40^{2 .} 4 Bytes = 19.2 kB

§ Otherwise, we would be bandwidth limited

# Flops

# Loads

# Flops/sec

# Loads/sec

= 2^.10¹² Flops/sec

200

4 ^.10⁹ B/sec

=

1 Load = 4 Bytes

= 40

(26)

Effects of Block Size

0 20 40 60 80 100 120 140 160 180 200

untiled 2x2 4x4 8x8 12x12 14x14 15x15 16x16

GFLOPS

Block size (m)

(27)

Comparison with MKL (Intel)

[ http://www.scribd.com/doc/47501296/CUDA-3-2-Math-Libraries-Performance]

(28)

Limitations / Optimality

§ Tiling/blocking only works, if the arithm. operation is associative

§ Arithmetic intensity, a, is bounded by size of shared memory, S:

§ Our algorithm performs many load operations

§ Note: in a sense, our blocked matrix multiplication algorithm is a way to schedule memory transfers and floating point operations

§ Theorem (Hong & Kung, 1981; w/o proof):

Any schedule of conventional matrix multiplication must transfer many floats between slow and fast memory.

§ In this sense, blocked matrix multiplication is optimal a ⇡ m 

rS 3 O n³

pS

O ^pⁿ³

S

(29)

Strassen's Algorithm

§ All "traditional" algorithms need O(n³) FLOPs

§ Strassen's algorithm: O(n^2.81)

§ Recursive algorithm!

§ See 2^nd semester's course "algorithms and data structures"

§ Current world record: O(n^2.376)

§ Strassen on the GPU?

§ Probably not worth it (recursion / complex control flow)

(30)

Application: All Pairs Shortest Paths (APSP)

§ Given: directed graph and a distance function

where V = set of all vertices (nodes), |V| = n, and E = set of edges

§ Goal: compute n×n matrix D = d_ij that stores for each pair (v_i, v_j) the length of the shortest path from v_i to v_j in graph G

§ Example:

1 2 3 4 5

1 0 3 8 4 4

2 3 0 6 1 7

3 7 4 0 5 11

4 2 5 5 0 6

5 8 11 11 6 0

1

2

3

4 5

2

1 3 4

8

4 5

6 7

Shortest path matrix D

G = (V,E)

dist : E ! R

(31)

The Adjacency Matrix Representation of Directed Graphs

§ The adjacency matrix A represents the distance function dist

§ A is an n×n matrix where

§ Example:

1 2 3 4 5

1 0 3 8 ∞ 4

2 ∞ 0 ∞ 1 7

3 ∞ 4 0 ∞ ∞

4 2 ∞ 5 0 ∞

5 ∞ ∞ ∞ 6 0

Adjacency matrix

A = ( _ij)

ij =

8>

<

>:

dist(v_i,v_j), if (v_i,v_j) 2 E 1, if (vi,vj) 2/ E

0, if i = j

1

2

3

4 5

2

1 3 4

8

4 5

6 7

(32)

The Shortest Paths Property

§ We will now extend the simple, edge-based distance function to a distance function dist' on paths

§ Define

§ Consider a shortest path p^k_ij from v_i to v_j such that , i.e., p^k_ij can have most k edges

§ Let (v_l, v_j) be the last edge of path p^k_ij

§ Then, there must be a shortest path from vi to vl (optimal substructure!)

§ Therefore,

|p_ij^k|  k dist’(p_ij¹) =

(0, i = j

ij, i 6= j

p_i^k_l ¹

9l : dist’(p_ij^k) = dist’(p_il^k ¹) + _lj

<latexit sha1_base64="P4k84djdM+V0pFdtO5NuPygfttQ=">AAACvHicbVFdaxQxFM2MH63rR3f10ZfgInaRLjNFUASl6IuPFdy20NkO2cydNp18DMlN7RLmh/roPzH7UepaL4QcTk7uuZw7a6VwmGW/kvTe/QcPt7Yf9R4/efpspz94fuSMtxwm3EhjT2bMgRQaJihQwklrgamZhONZ83XxfnwF1gmjf+C8hali51rUgjOMVNkPBVxHF0cLxfBCYJAd/UgL04JlaKxmCkIVBW+63fasKYO47Eb00/8FtD0LzV7eRdVtt46O6FtaVCCRleGWv+x6ZX+YjbNl0bsgX4MhWddhOUhGRWW4V6CRS+bcab7f4jQwi4JL6HqFd9Ay3rBzCMtsOvo6UhWtjY1HI12yGzo1X8wUhYvL/f106rH+MA1Ctx5B81Wv2kuKhi6ypJWwwFHOKeM8juQZRit+wSzjGDPfsHFMu5VRcQN7hQUNP7lRiukqFDVTQs4rqJmX2IXC1Td4s5PwWuB1JJ1wgL4NcRd7ylQQF1MvvONmuxhu/m+Ud8HR/jjPxvn3d8ODL+uYt8lL8orskpy8JwfkGzkkE8LJ72Qr6SeD9HNapU2qVtI0Wf95QTYqvfoDI5ncbA==</latexit><latexit sha1_base64="P4k84djdM+V0pFdtO5NuPygfttQ=">AAACvHicbVFdaxQxFM2MH63rR3f10ZfgInaRLjNFUASl6IuPFdy20NkO2cydNp18DMlN7RLmh/roPzH7UepaL4QcTk7uuZw7a6VwmGW/kvTe/QcPt7Yf9R4/efpspz94fuSMtxwm3EhjT2bMgRQaJihQwklrgamZhONZ83XxfnwF1gmjf+C8hali51rUgjOMVNkPBVxHF0cLxfBCYJAd/UgL04JlaKxmCkIVBW+63fasKYO47Eb00/8FtD0LzV7eRdVtt46O6FtaVCCRleGWv+x6ZX+YjbNl0bsgX4MhWddhOUhGRWW4V6CRS+bcab7f4jQwi4JL6HqFd9Ay3rBzCMtsOvo6UhWtjY1HI12yGzo1X8wUhYvL/f106rH+MA1Ctx5B81Wv2kuKhi6ypJWwwFHOKeM8juQZRit+wSzjGDPfsHFMu5VRcQN7hQUNP7lRiukqFDVTQs4rqJmX2IXC1Td4s5PwWuB1JJ1wgL4NcRd7ylQQF1MvvONmuxhu/m+Ud8HR/jjPxvn3d8ODL+uYt8lL8orskpy8JwfkGzkkE8LJ72Qr6SeD9HNapU2qVtI0Wf95QTYqvfoDI5ncbA==</latexit><latexit sha1_base64="P4k84djdM+V0pFdtO5NuPygfttQ=">AAACvHicbVFdaxQxFM2MH63rR3f10ZfgInaRLjNFUASl6IuPFdy20NkO2cydNp18DMlN7RLmh/roPzH7UepaL4QcTk7uuZw7a6VwmGW/kvTe/QcPt7Yf9R4/efpspz94fuSMtxwm3EhjT2bMgRQaJihQwklrgamZhONZ83XxfnwF1gmjf+C8hali51rUgjOMVNkPBVxHF0cLxfBCYJAd/UgL04JlaKxmCkIVBW+63fasKYO47Eb00/8FtD0LzV7eRdVtt46O6FtaVCCRleGWv+x6ZX+YjbNl0bsgX4MhWddhOUhGRWW4V6CRS+bcab7f4jQwi4JL6HqFd9Ay3rBzCMtsOvo6UhWtjY1HI12yGzo1X8wUhYvL/f106rH+MA1Ctx5B81Wv2kuKhi6ypJWwwFHOKeM8juQZRit+wSzjGDPfsHFMu5VRcQN7hQUNP7lRiukqFDVTQs4rqJmX2IXC1Td4s5PwWuB1JJ1wgL4NcRd7ylQQF1MvvONmuxhu/m+Ud8HR/jjPxvn3d8ODL+uYt8lL8orskpy8JwfkGzkkE8LJ72Qr6SeD9HNapU2qVtI0Wf95QTYqvfoDI5ncbA==</latexit><latexit sha1_base64="P4k84djdM+V0pFdtO5NuPygfttQ=">AAACvHicbVFdaxQxFM2MH63rR3f10ZfgInaRLjNFUASl6IuPFdy20NkO2cydNp18DMlN7RLmh/roPzH7UepaL4QcTk7uuZw7a6VwmGW/kvTe/QcPt7Yf9R4/efpspz94fuSMtxwm3EhjT2bMgRQaJihQwklrgamZhONZ83XxfnwF1gmjf+C8hali51rUgjOMVNkPBVxHF0cLxfBCYJAd/UgL04JlaKxmCkIVBW+63fasKYO47Eb00/8FtD0LzV7eRdVtt46O6FtaVCCRleGWv+x6ZX+YjbNl0bsgX4MhWddhOUhGRWW4V6CRS+bcab7f4jQwi4JL6HqFd9Ay3rBzCMtsOvo6UhWtjY1HI12yGzo1X8wUhYvL/f106rH+MA1Ctx5B81Wv2kuKhi6ypJWwwFHOKeM8juQZRit+wSzjGDPfsHFMu5VRcQN7hQUNP7lRiukqFDVTQs4rqJmX2IXC1Td4s5PwWuB1JJ1wgL4NcRd7ylQQF1MvvONmuxhu/m+Ud8HR/jjPxvn3d8ODL+uYt8lL8orskpy8JwfkGzkkE8LJ72Qr6SeD9HNapU2qVtI0Wf95QTYqvfoDI5ncbA==</latexit><latexit sha1_base64="P4k84djdM+V0pFdtO5NuPygfttQ=">AAACvHicbVFdaxQxFM2MH63rR3f10ZfgInaRLjNFUASl6IuPFdy20NkO2cydNp18DMlN7RLmh/roPzH7UepaL4QcTk7uuZw7a6VwmGW/kvTe/QcPt7Yf9R4/efpspz94fuSMtxwm3EhjT2bMgRQaJihQwklrgamZhONZ83XxfnwF1gmjf+C8hali51rUgjOMVNkPBVxHF0cLxfBCYJAd/UgL04JlaKxmCkIVBW+63fasKYO47Eb00/8FtD0LzV7eRdVtt46O6FtaVCCRleGWv+x6ZX+YjbNl0bsgX4MhWddhOUhGRWW4V6CRS+bcab7f4jQwi4JL6HqFd9Ay3rBzCMtsOvo6UhWtjY1HI12yGzo1X8wUhYvL/f106rH+MA1Ctx5B81Wv2kuKhi6ypJWwwFHOKeM8juQZRit+wSzjGDPfsHFMu5VRcQN7hQUNP7lRiukqFDVTQs4rqJmX2IXC1Td4s5PwWuB1JJ1wgL4NcRd7ylQQF1MvvONmuxhu/m+Ud8HR/jjPxvn3d8ODL+uYt8lL8orskpy8JwfkGzkkE8LJ72Qr6SeD9HNapU2qVtI0Wf95QTYqvfoDI5ncbA==</latexit>

(33)

A Simple Algorithm for APSP

§ Given the adjacency matrix A, compute a series of matrices

D¹=A, D², …, D^n-2, D^n-1 where matrix contains lengths of shortest paths in G with at most k edges

§ Example:

§ Final matrix D^n-1 contains the actual shortest paths in G D^k = dist’(p_ij^k)

1 2 3 4 5

1 0 3 8 4 4

2 3 0 6 1 7

3 ∞ 4 0 5 11

4 2 5 5 0 6

5 8 ∞ 11 6 0

Matrix D²

1

2

3

4 5

2

1 3 4

8

4 5

6 7

1 2 3 4 5

1 0 3 8 ∞ 4

2 ∞ 0 ∞ 1 7

3 ∞ 4 0 ∞ ∞

4 2 ∞ 5 0 ∞

5 ∞ ∞ ∞ 6 0

Adjacency matrix

(34)

§ The algorithm:

§ Notice the similarity with matrix multiplication

§ We can adapt our fast GPU-based matrix multiplication code to solve the APSP problem quite easily (just replace operators in line (*)

A = adjacency matrix D¹ = A

for k = 2 to n-1:

D^k = ExtendPaths(D^k-1, A) return D^k

ExtendPaths( D, A )

In: A (with δij) = n×n adj. matrix Out: E (with e_ij) = n×n dist. matrix for i = 1 to n:

for j = 1 to n:

e_ij = d_ij

for l = 1 to n:

e_ij = min{e_ij, d_il + δ_lj) return E

MatrixMultiply( B, A )

In: A = (δ_ij) = n×n input matrix Out: C = (c_ij)= n×n matrix prod.

for i = 1 to n:

for j = 1 to n:

c_ij = 0

for l = 1 to n:

c_ij = c_ij + a_il^.b_lj (*) return C

(35)

A Word on Sparse Matrices

§ Just some remarks

§ Frequent case: sparse band matrices

§ Represent matrix as a number of vectors

§ Devise specialized parallel algorithm (similar to vector addition)

2 vectors

(36)

§ Many more kinds of sparse matrices

§ Specialized representation / algorithms for each of them?

(37)

Summary

§ Simple performance models can aid in understanding

§ Two ratios are key:

§ Arithmetic (computational) intensity =

- "flops" = floating point operations, "mops" = memory operations

§ Machine balance =

# flops

# mops

Tflops/sec GB/sec