Simulation von Diffusions-Adsorptionsprozessen in natürlichem Gesteinsmaterial mit COMSOL Multiphysics

Simulation von

Diffusions-Adsorptionsprozessen in natürlichem Gesteinsmaterial mit

COMSOL Multiphysics

Diplomarbeit

im Studiengang Chemie-Ingenieurwesen der Technischen Universität Dresden

zur Erlangung des akademischen Grades Diplomingenieur (Dipl.-Ing.)

Johannes Schikora

geboren am 09.08.1986 in Halle/Saale

Hochschullehrer: Prof. Dr.-Ing. habil. W. Klöden

(TU Dresden)

Betreuer: Dr. J. Lippmann-Pipke

(HZDR/IRE) Dr. V. Brendler

(HZDR/IRE)

Bearbeitungszeitraum: 14.11.2011 bis 13.03.2012

(Verlängerung bis 13.04.2012)

Dresden, April 2012

Aufgabenstellung II

Aufgabenstellung

Thema: Simulation von Diffusions-Adsorptionsprozessen in natürlichem Gesteinsmaterial mit COMSOL Multiphysics

Der Transport chemisch-toxischer und radioaktiver Kontaminanten in geo- logischen Formationen istdurchSimulation der Diffusions-Adsorptionsprozesse in natürlichem Gesteinsmaterial mit Hilfe COMSOL Multiphysics zu untersu- chen. Der diffusive Transport spielt eine wichtige Rolle in Ausbreitungsrechnun- gen und damit in der Risikoabschätzung entsprechender untertägiger Deponien und Endlager. Die anzufertigende Arbeit soll als Hauptziele die Nachrechnung vorhandener Experimente zur Parameterschätzung sowie die prognostische Modellierung zur Optimierung von Diffusionsexperimenten verfolgen.

Im Einzelnen sind folgende Aufgaben zu lösen:

 Einarbeitung in COMSOL Multiphysics 4.2 und das Ergänzungsmodul Che- mical Reaction Engineering auch mit dem Ziel des weiteren Ausbaus der Nutzerkompetenz am Institut für Radiochemie.

 Auswahl geeigneter Interfaces aus dem COMSOL Basismodul und ggf. dem Chemical Engineering Module für die Nachrechnung vorhandener Datensätze.

 Es sind ausgewählte explizite Diffusions- und Diffusions-Adsorptions- experimente zu simulieren. Die Parameterbestimmung ist durch Daten- abgleich zu gewährleisten. Darüber hinaus ist eine Auswahl alternativer Mo- delle zu testen und zu vergleichen; beispielsweise hinsichtlich der jeweils zu Grunde liegenden Gleichungen, der Porosität oder der Raum-Zeit-Skala.

 Für ein geplantes Diffusionsexperiment ist mittels prognostischer Rechnun- gen eine Optimierung der variablen Parameter vorzunehmen.

Betreuer : Dr. J. Lippmann-Pipke (HZDR / IRE) Dr. V. Brendler (HZDR / IRE)

Tag der Ausgabe: 14. November 2011

Tag der Abgabe: 13. März 2012 (Verlängerung bis 13. April 2012)

Die von der Studienrichtung erlassenen Richtlinien zur Anfertigung der Diplomarbeit sowie die Diplomprüfungsordnung sind zu beachten.

Prof. Dr.-Ing. habil. Lange Prof. Dr.-Ing. habil. Klöden Geschäftsführender Direktor des Instituts Betreuender Hochschullehrer

Danksagung

Die vorliegende Diplomarbeit wurde in der Abteilung für Reaktiven Transport am In- stitut für Ressourcenökologie (vormals Radiochemie) des Helmholtz-Zentrums Dres- den-Rossendorf e.V. verfasst.

An dieser Stelle möchte ich mich bei allen Personen bedanken, die durch ihre tatkräf- tige Unterstützung zum Entstehen dieser Arbeit beigetragen haben.

Dabei gilt mein ganz besonderer Dank meiner Betreuerin Frau Dr. Lippmann-Pipke.

Sie hat mich mit hoher fachlicher Kompetenz und großem persönlichen Engagement sowohl bei meiner wissenschaftlichen Arbeit unterstützt, als mir auch durch die er- möglichte Teilnahme an einer wissenschaftlichen Konferenz Gelegenheit gegeben, die Ergebnisse meiner Arbeit einem Fachpublikum vorzustellen.

Auch bei Herrn Dr. Brendler möchte ich mich für seine Betreuung herzlich bedanken.

Wie schon bei der Erarbeitung des Großen Belegs, so auch bei der Diplomarbeit, stand er mir mit seinem Fachwissen und Ratschlägen jederzeit zur Seite.

Weiterhin bedanken möchte ich mich bei Herrn Professor Klöden für die fachliche Betreuung dieser Arbeit seitens der Technischen Universität Dresden sowie bei Dr.

Johannes Kulenkampff und Claudia Joseph für das zur Verfügung stellen ihrer Mess- daten.

Meiner Familie, insbesondere meinen Eltern und zukünftigen Schwiegereltern, ge- bührt ebenfalls großer Dank, da sie durch ihre moralische und finanzielle Unterstüt- zung einen wichtigen Beitrag zur Anfertigung der Diplomarbeit geleistet haben. Auch meiner Verlobten Anne möchte ich ganz herzlich dafür danken, dass sie mir unermüd- lich mit Rat und Tat zur Seite stand und in schwierigen Zeiten immer ein aufmun- terndes Wort und Verständnis für mich hatte

Inhaltsverzeichnis 4

Inhaltsverzeichnis

Aufgabenstellung...II Danksagung ... III

Inhaltsverzeichnis...4

Abkürzungs- und Symbolverzeichnis...7

1 Einleitung und Motivation...11

2 Charakterisierung des natürlichen Gesteins Opalinuston ...13

2.1 Entstehung und Verbreitung...13

2.2 Zusammensetzung und chemisch-physikalische Eigenschaften ...14

3 Theoretische Grundlagen der Diffusion und Sorption...16

3.1 Diffusion...16

3.1.1 Fick’sche Gesetze ...16

3.1.2 Diffusion in porösen Medien...20

3.2 Sorptionsisothermen ...22

3.2.1 Grundlagen der Sorption...22

3.2.2 Lineare (Henry-)Isotherme ...23

3.3 Diffusion unter Berücksichtigung von Sorption ...24

3.4 Notwendigkeit der Transportparameterschätzung mittels numerischer Simulation...24

4 Theoretische Grundlagen der Parameterschätzung...27

4.1 Einleitung...27

4.2 Methode der kleinsten Quadrate ...28

4.2.1 Lineare Ausgleichsprobleme ...28

4.2.2 Nichtlineare Ausgleichsprobleme ...30

4.3 Numerische Optimierungsalgorithmen ...30

4.3.1 Verfahren des steilsten Abstiegs ...30

4.3.2 Gauss-Newton-Algorithmus ...31

4.3.3 Levenberg-Marquardt-Algorithmus ...32

4.4 Regularisierungsmethoden ...33

4.4.1 Einführung zu schlecht-gestellten Problemen ...33

4.4.2 Tikhonov-Regularisierung...34

4.4.3 Umsetzung von Regularisierungsmethoden in COMSOL 4.2a...35

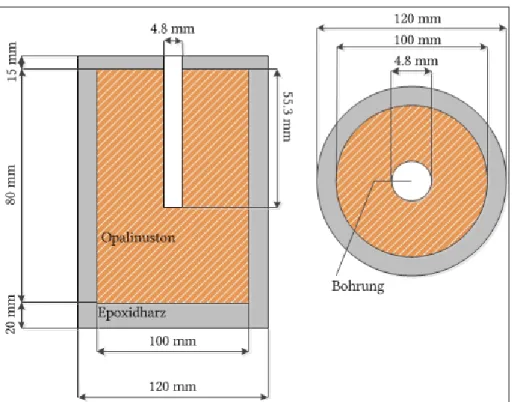
5 Experimentelle Methoden...39

5.1 Quantifizierung der 1D Diffusion mittels Diffusionszelle...39

5.1.1 Konservative Diffusionsstudie mit HTO ...39

5.1.2 Reaktive Diffusionsstudie mit ²³³U(VI) ...42

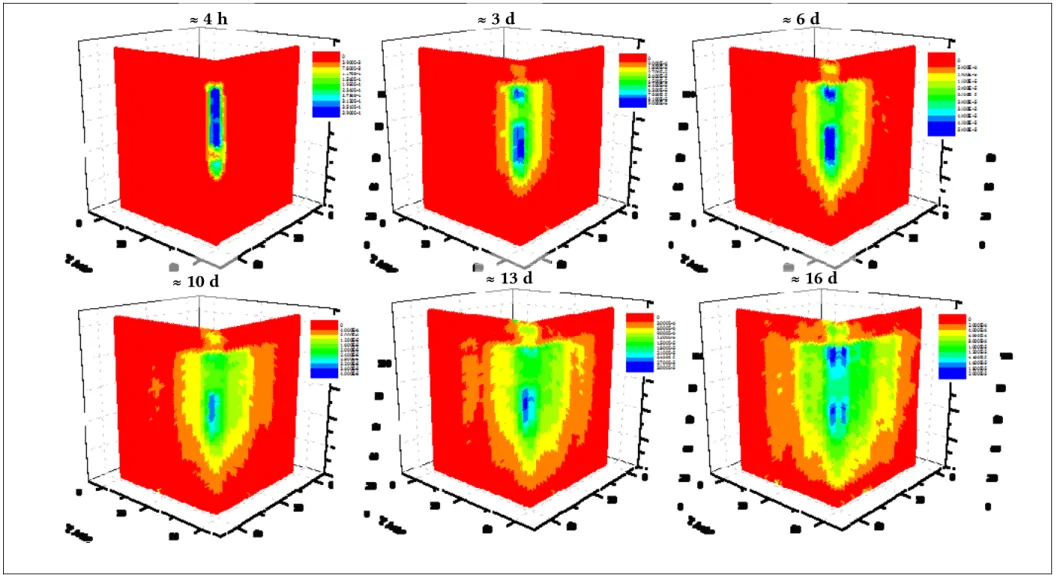
5.2 Visualisierung der 3D Diffusion mittels der GeoPET-Methode...42

5.2.1 Positronen-Emissions-Tomographie (PET)...42

5.2.2 Reaktive Diffusionsstudie mit ²²Na⁺...44

6 Modellierung und Simulation der Experimente mit COMSOL Multiphysics...47

6.1 COMSOL Multiphysics ...47

6.2 Exkurs: Die Finite-Elemente-Methode ...48

6.3 Auswahl eines geeigneten Interfaces für die Modellierung und Simulation der Experimente ...52

6.3.1 Transport verdünnter Spezies...53

6.3.2 Speziestransport in porösen Medien ...53

6.3.3 Mathematik-Interface ...54

6.3.4 Ergebnis der Auswahlprozedur ...55

6.4 Umsetzung der Experimente ...56

6.4.1 1D-Diffusionszelle ...56

6.4.2 Zerstörungsfreie 3D-Beobachtung mittels GeoPET...58

7 Ergebnisse und Diskussion ...62

7.1 1D-Diffusionszelle...62

7.1.1 Konservative Diffusionsstudie mit HTO ...62

7.1.2 Reaktive Diffusionsstudie mit ²³³U(VI) ...69

7.2 Zerstörungsfreie 3D-Beobachtung mittels GeoPET...72

7.2.1 Ergebnisse der Parameterschätzung...72

7.2.2 Lokale Sensitivitätsanalyse der Modellparameter...78

7.2.3 Optimierungsempfehlung für zukünftige Experimente mittels GeoPET ...81

8 Zusammenfassung und Ausblick ...83

9 Literaturverzeichnis ...86

Abbildungsverzeichnis...90

Tabellenverzeichnis...92

Thesen zur Diplomarbeit...93

Eidesstattliche Erklärung...95 A Messdaten der konservativen Diffusionsstudie mit HTO...A B Messdaten der reaktiven Diffusionsstudie mit ²³³U(VI) ... C

Inhaltsverzeichnis 6

C Messzeitpunkte der reaktiven Langzeitdiffusionsstudie ... I D Langzeitdiffusionsstudie mittels GeoPET (Abbildungen)... J

Abkürzungs- und Symbolverzeichnis

Abkürzungsverzeichnis/Glossar

Begriff Bedeutung/ Erklärung

Nagra Nationale Genossenschaft für die Lagerung von radioak- tiven Abfällen (Schweiz)

low-Reservoir Reservoir ohne Tracer oder nur einer sehr geringen Men- ge an Tracer

high-Reservoir Reservoir mit Tracer im Überschuss (c ≈ const.) Modellbuilder

(COMSOL)

Übersicht zum Erstellen und Verwalten des COMSOL- Modells

Interface (COMSOL) bereits speziell zugeschnittenes physikalische Gesetz Parameter Sweep

(COMSOL)

automatisches, mehrfaches Berechnen des COMSOL- Modells mit vorgegebenen, variierenden Werten eines Pa- rameters

abrasive peeling schichtweises Abtragen einer Gesteinsprobe

Symbolverzeichnis

Symbol Einheit Beschreibung

 [-] allgemeine Bilanzgröße, Ansatzfunktion (Methode der finiten Elemente)

A m2 Fläche

A Modellmatrix (des chem. Modells)

a(s,m) Kernel

b Messdaten

c mol/m3 Spezieskonzentration im Fluid (z.B. Porenwasser)

Abkürzungs- und Symbolverzeichnis 8

Symbol Einheit Beschreibung

c0 mol/m3 Anfangskonzentration

ci Wert der Ansatzfunktion am Punkt xi

cs mol/kg Konzentration des angelagerten Sorptivs

d m Durchmesser, Dicke

D m2/s (binärer) Diffusionskoeffizient

da Dämpfungsfaktor im PDGL-Modus von COMSOL

Da m2/s scheinbarer (eng. Apparent) Diffusionskoeffizient Daq m2/s Diffusionskoeffizient einer Spezies in Wasser

De m2/s effektiver Diffusionskoeffizient

Dij m2/s Diffusionskoeffizient in Richtung i bei Gradient in Richtung j

dPore m Porendurchmesser

dSpezies m Speziesdurchmesser

F Fehlerquadratsumme

f Quellterm

G [-] Geometriefaktor

h Schrittweite

I Einheitsmatrix

j mol/(m2·s) diffusiver Massenstrom

J Jacobimatrix

Kd m3/kg Verteilungskoeffizient, Kd-Wert

kp Term für die Sorptionsisotherme (in COMSOL)

L Tikhonov- oder roughening-Matrix

l m kürzester Weg durch das Bilanzgebiet

leff m effektiver/ tatsächlich zurückgelegter Weg

m kg Masse

n mol Stoffmenge

Symbol Einheit Beschreibung

q mol/(m3·s) allgemeiner Massenstrom (molekular o. konvektiv)

r Residuum

R Reaktionsterm

S Senkenterm

t s Zeit

u m/s Geschwindigkeitsfeld

v Testfunktion (Methode der finiten Elemente)

V m3 Volumen

Vges m3 Gesamtvolumen

VH m3 Hohlraumvolumen

x m Raumkoordinate, kartesisches Koordinatensystem oder allgemeiner Parameter

x Lösungsmatrix, Parametermatrix

x0 Entwicklungsstelle

x1, x2 Regressionsparameter, allgemeiner Parameter y m Raumkoordinate, kartesisches Koordinatensystem

oder allgemeine Funktion

z m Raumkoordinate, kartesisches Koordinatensystem α [-] Gesteins-Kapazitätsfaktor oder Schrittweitenpara-

meter

β m/s Konvektionstensor

δ [-] Konstriktivität

ε [-] Porosität (gesamt) des Materials

εt [-] transportwirksame Porosität

λ [-] Regularisierungsparameter

λLM [-] Dämpfungsfaktor im Levenberg-Marquardt- Algorithmus

Abkürzungs- und Symbolverzeichnis 10

Symbol Einheit Beschreibung

λp [-] Verhältnis aus Teilchen- und Porendurchmesser

ρ kg/m3 Dichte des Materials

ρb kg/m3 Bulkdichte des Materials (trocken)

σ Standardabweichung

τ [-] Tortuosität

1 Einleitung und Motivation

Viele Länder innerhalb Europas, wie zum Beispiel Frankreich, Deutschland oder die Schweiz, produzieren einen (großen) Teil ihres Energiebedarfs über Kernkraft. Zwar hat Deutschland den Ausstieg aus der Atomenergie beschlossen, sodass perspektivisch kein neuer radioaktiver Abfall aus Kraftwerken anfällt, trotzdem besteht auch danach die Notwendigkeit der Entsorgung von radioaktiven Stoffen aus der Industrie, For- schung und Medizin. Eine Option für die Entsorgung von radioaktiven Stoffen aus diesen Branchen sowie aus dem Betrieb und der Stilllegung von Kernkraftwerken ist die geologische Tiefenlagerung. Dafür geeignetes Wirtsgestein muss als Bestandteil des Multibarrierenkonzepts bestimmte Anforderungen erfüllen. Dieses Konzept soll den Einschluss der Kontaminanten über sehr lange Zeiträume garantieren, bis die Ak- tivität der Abfälle auf ein unbedenkliches Maß abgefallen ist. So sollte das gewählte Wirtsgestein eine möglichst geringe hydraulische Leitfähigkeit aufweisen. Der domi- nante Transportmechanismus ist dann die Diffusion und die Ausbreitung von Schad- stoffen findet in solchen Gesteinen verlangsamt statt. Eine weitere Eigenschaft des Gesteins sollte seine Fähigkeit sein, den Transport von Kontaminanten durch Sorption zu retardieren.

Als potentielles Wirtsgestein für radioaktiven Abfall wird in der Schweiz der Opali- nuston des Zürcher Weinlandes untersucht. Er weist die oben beschriebene Eigen- schaft einer (sehr) geringen hydraulischen Leitfähigkeit (1·10^-14 – 1·10^-13 m/s) auf (Nagra, 2002). Es ist daher zu erwarten, dass der Transport von gelösten Substanzen innerhalb des Opalinuston durch Diffusion erfolgt. Des Weiteren bedingt der hohe Anteil an Tonmineralen in diesem Wirtsgestein eine gute Retardierung von Kontami- nanten. Auch in Deutschland sind Tongesteine, wie der Opalinuston, Untersuchungs- gegenstand im Zusammenhang mit der Lagerung von radioaktiven Abfällen und bei der Suche nach Alternativen zu Gorleben (Hoth et al., 2007)

Der diffusive Transport spielt somit eine wichtige Rolle in Ausbreitungsrechnungen und damit in der Risikoabschätzung entsprechender untertägiger Deponien und End- lager. Für Langzeitsicherheitsanalysen werden neben einem guten Systemverständnis auch die Parameter der Transportgleichungen benötigt. Eine mögliche Vorgehenswei- se bei der Bestimmung von Transportparametern ist das Durchführen von Laborexpe- rimenten. Die zugrundeliegenden Bilanzgleichungen lassen sich jedoch nicht in jedem Fall analytisch lösen. Es ist dadurch notwenig numerische Lösungsmethoden zu nut- zen, zum Beispiel in Computersimulationen.

Einleitung und Motivation 12

Gegenstand der vorliegenden Arbeit ist es, den Transport chemisch-toxischer und ra- dioaktiver Kontaminanten in geologischen Formationen durch Simulation der Diffusi- ons-Adsorptionsprozesse in natürlichem Gesteinsmaterial zu untersuchen. Als Simula- tionsumgebung kommt dabei COMSOL Multiphysics zum Einsatz. Sie nutzt zur nume- rischen Lösung von partiellen Differentialgleichungen die Methode der finiten Ele- mente. Hauptziele, die in der vorliegenden Arbeit mit Hilfe der Modellbildung und Simulation der Transportprozesse erreicht werden sollen, sind die Nachrechnung vor- handener Experimente zur Parameterschätzung sowie prognostische Rechnungen zur Optimierung von Diffusionsexperimenten. Es sollen des Weiteren die Möglichkeiten des Simulationstools COMSOL Multiphysics zur effektiven Auswertung von komple- xen, dreidimensionalen und anisotropen Daten aus zeitabhängigen Transportuntersu- chungen evaluiert werden.

Im Einzelnen werden die folgenden Teilaufgaben gelöst:

 Einarbeitung in COMSOL Multiphysics 4.2/4.2a, das Ergänzungsmodul Chemi- cal Reaction Engineering sowie das Optimierungsmodul auch mit dem Ziel des weiteren Ausbaus der Nutzerkompetenz am Institut für Ressourcenökologie (vormals Institut für Radiochemie).

 Auswahl geeigneter Interfaces aus dem COMSOL Basismodul und ggf. dem Chemical Engineering Module für die Nachrechnung vorhandener Datensätze.

 Es sind ausgewählte explizite Diffusions- und Diffusions-Adsorptions- experimente zu simulieren. Die Parameterbestimmung ist durch Datenabgleich zu gewährleisten. Darüber hinaus ist eine Auswahl alternativer Modelle zu tes- ten und zu vergleichen; beispielsweise hinsichtlich der jeweils zu Grunde lie- genden Gleichungen, der Porosität oder der Raum-Zeit-Skala.

 Für ein geplantes Diffusionsexperiment ist mittels prognostischer Rechnungen eine Optimierung der variablen Parameter vorzunehmen.

2 Charakterisierung des natürlichen Gesteins Opalinuston

2.1 Entstehung und Verbreitung

Als einführendes Kapitel soll einer der Hauptbestandteile der hier untersuchten Sys- teme vorgestellt werden – das natürliche Gestein Opalinuston. Aus seinen Eigenschaf- ten ergibt sich der Rahmen, in dem sich die Modellierungs- und Simulationsarbeiten nachfolgend bewegen. Falls nicht ausdrücklich anders angegeben, beziehen sich die Ausführungen in diesem Abschnitt auf die Technischen Berichte 02-03 und 05-02 der Nagra (Nationale Genossenschaft für die Lagerung von radioaktiven Abfällen, Schweiz).

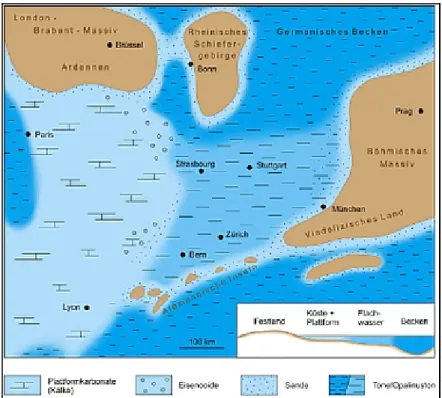
Die Formation des Opalinustons ist ein feinkörniges Sedimentgestein mit einer Mäch- tigkeit von ca. 80 – 120 m. Sie ist in der Nordschweiz und den angrenzenden Ländern zu finden. Vor ca. 180 Mio. Jahren war dieses Gebiet mit einem flachen, auf kontinen- talem Grund liegenden Meer bedeckt (siehe Abbildung 1). In diesem konnten sich Tonpartikel gleichmäßig ablagern und ein Schichtenpaket aufbauen.

Abbildung 1: Paläogeografische Verhältnisse zu Beginn der Ablagerung des Opalinuston.

Quelle: (Nagra, 2005)

Charakterisierung des natürlichen Gesteins Opalinuston 14

Seinen Namen hat der Opalinuston von dem häufig in ihm zu findenden Ammoniten Leioceras opalinum erhalten (früher: Ammonitas opalinus). Ein solches Fossil wurde zum Beispiel auch in der Sondierbohrung Benken (Schweiz) gefunden.

Abbildung 2: Der Ammonit Leioceras opalinum aus der Sondierbohrung Benken in der Schweiz. Quelle: (Nagra, 2003)

Nach der Ablagerung der Tonpartikel kam es zu einer allmählichen Verfestigung der gebildeten Schicht und, durch die Auflast jüngerer Sedimente, zu ihrer Kompaktier- ung. Dabei richteten sich die Tonplättchen senkrecht zur Belastung aus. Die Kompres- sion des Sediments bewirkte eine Reduktion der Porosität und das Auspressen des eingeschlossenen (Poren-)Wassers. Während der Versenkung und Kompaktierung war der Opalinuston Temperaturen von 80 -90 °C ausgesetzt.

2.2 Zusammensetzung und chemisch-physikalische Eigenschaften

Der Opalinuston in der Nordschweiz besteht aus feinkörnigen, kontinentalen Verwit- terungs- und Erosionsprodukten (Tonminerale, Quarz, Feldspäte) sowie aus marinen Karbonaten (Muscheln, Bioklaste) und diagenetischen Neubildungen (Pyrit, Siderit, Calcit-Zement). Des Weiteren enthält er organisches Material. Laut Nagra (2005) ist er in seiner horizontalen Ausbreitung ein relativ homogenes Sediment. Somit sind auch seine Wirtsgesteineigenschaften über große Distanzen extrapolierbar. Typische Wer- tebereiche für die Mineralzusammensetzung eines Opalinustones in der Nordschweiz sind in Tabelle 1 zusammengestellt. Charakteristische Werte für die Porosität von Opalinuston liegen im Bereich 0.09 ≤  ≤ 0.17 und für seine Dichte im Bereich 2270 kg/m3≤  ≤ 2490 kg/m3 (Gimmi & Kosakowski 2011, Supporting Information).

Tabelle 1: Typische prozentuale Zusammensetzung von Opalinustonvorkommen in der Nordschweiz (Nagra, 2005).

Mineral Gewichtsprozent Tonminerale (Illit, Kaolinit, Chlorit,

Illit/Smektit-Wechsellagerungsminerale) 40 – 80

Quarz 15 – 30

Calcit 6 – 40

Siderit 2 – 3

Pyrit 1 – 3

organischer Kohlenstoff 0.5 – 1

Durch die während seiner Versenkung vorherrschenden Bedingungen (hoher Druck und hohe Temperatur) erhielt der Opalinuston eine seiner für die Endlagerung und den Stofftransport zentralen Eigenschaften: eine (sehr) geringe hydraulische Leitfä- higkeit (2·10^-14 bis 1·10^-13 m/s). Somit dominiert als Stofftransportprozess die Diffusi- on.

Auf Grund der im Opalinuston vorhandenen quellfähigen Minerale besitzt er ein sehr gutes Abdichtungs- und Isolationsvermögen. Durch dieses Selbstabdichtungsvermö- gen haben auch Störungen eine geringe hydraulische Durchlässigkeit, was eine vor- wiegend diffusive Ausbreitung von Kontaminanten unterstützt.

Durch den hohen Anteil an Schichtsilikaten (z.B.: Illit, Kaolinit und Chlorit) erhält der Opalinuston anisotrope Materialeigenschaften, welche in der Modellierung der Diffu- sion zu berücksichtigen sind. Der hohe Anteil an Tonmineralen bedingt außerdem ei- ne große Retardation (Sorption) von z.B. Radionukliden.

Zusammenfassend ergeben sich die folgenden, für die Simulation von Opalinuston, wichtigen Eigenschaften, welche bei der Modellbildung berücksichtigt werden sollten:

 Vorherrschender Transportmechanismus ist die Diffusion

 Opalinuston ist ein anisotropes Material

 Im Porenwasser gelöste Spezies können sorbieren

Nachfolgend werden die theoretischen Grundlagen der Diffusion erläutert und es werden die benötigten Gleichungen so erweitert, dass sie die obigen Eigenschaften des Opalinuston wiedergeben können.

Theoretische Grundlagen der Diffusion und Sorption 16

3 Theoretische Grundlagen der Diffusion und Sorption

3.1 Diffusion

Allgemein ist Diffusion ein freiwillig ablaufender, irreversibler, physikalischer Pro- zess, der zu einer Entropiezunahme im System führt. Auf die regellose thermische Ei- genbewegung von chemischen Spezies bezogen, wird diese auch als Brownsche Mole- kularbewegung bezeichnet. Statistisch bewegen sich dabei mehr Teilchen aus Gebie- ten hoher in Gebiete niedriger Konzentration, sodass ein Nettostoffstrom zu beobach- ten ist (makroskopischer Stofftransport). Dieser ist proportional zum anliegenden Konzentrationsgradienten zwischen den beiden Gebieten. Diffusion führt in geschlos- senen Systemen zur vollständigen Durchmischung der Teilchen und somit zum Abbau von Konzentrationsgradienten. Auch nach der Durchmischung unterliegen die Teil- chen der Brownschen Molekularbewegung, sie wandern also zwischen den ehemali- gen Gebieten hoher und niedriger Konzentration. Auf makroskopischer Ebene ist je- doch keine Konzentrationsänderung mehr feststellbar. Nachfolgend wird unter Diffu- sion in dieser Arbeit der oben beschriebene Nettostoffstrom verstanden. Diffusions- prozesse auf Grund anderer Gradienten als dem Konzentrationsgradienten, z.B. durch Temperaturgradienten, sind nicht Gegenstand der Diplomarbeit.

Das oben beschriebene Verhalten von Molekülen und Atomen lässt sich mathematisch durch die Fick’schen Gesetze beschreiben. Sie wurden 1855 auf empirischer Basis von Adolf Fick aufgestellt (Fick, 1855) und konnten später von Albert Einstein auf Basis thermodynamischer Überlegungen abgeleitet werden (Einstein, 1905).

3.1.1 Fick’sche Gesetze

3.1.1.1 Isotropes Medium

Die eigentliche Triebkraft für den Netto-Teilchenstrom ist ein Gradient des chemi- schen Potentiales. Im Allgemeinen können die Fick’schen Gesetze aber auch mit Hilfe der Konzentration formuliert werden. Der Diffusionsstrom j einer chemischen Spe- zies, eines Moleküls oder Atoms, also die Anzahl an Teilchen die sich pro Zeiteinheit durch eine bestimmte Referenzfläche bewegen, wird über das 1. Fick’sche Gesetz wie folgt beschrieben:

· c

  D

j (3.1)

j ist der Diffusionsstrom der Spezies in mol/(m2·s), D ist der binäre Diffusionskoeffi- zient der betrachteten Spezies im untersuchten Material in m2/s und c die Konzentra- tion der Spezies in mol/m3.

Im Rahmen dieser Arbeit werden nur Diffusionsprozesse von chemischen Spezies be- trachtet, die im Porenwasser des natürlichen Gesteins stattfinden. Dementsprechend bezeichnet c hier die Spezieskonzentration im Fluid (Porenwasser oder freies Medium).

Bei der Annahme, dass es sich um Diffusion in einem isotropen Medium handelt, ist D ein Skalar. Das negative Vorzeichen von D ergibt sich aus der Definition des Gradien- ten. Er ist in der Mathematik so definiert, dass er in die Richtung der stärksten Funkti- onsänderung zeigt, also in Richtung des größten Anstiegs. Diffusion erfolgt jedoch von hoher zu niedriger Konzentration, also entgegen des Gradienten. Damit ein posi- tiver Diffusionskoeffizient verwendet werden kann, wird das Minuszeichen einge- führt. Ausgeschrieben hat das 1. Fick’sche Gesetz für eindimensionale Diffusion fol- gende Form:

·

=-D c x



j  (3.2)

bzw. für den dreidimensionalen Fall:

=- · c c c

D x y z

    

   

 

j (3.3)

Mit Hilfe der Kontinuitätsgleichung lässt sich aus dem 1. Fick’schen Gesetz das 2.

Fick’sche Gesetz ableiten. Es beschreibt die zeitliche Entwicklung der Konzentration einer Spezies innerhalb des betrachteten Gebietes.

Allgemein lässt sich die zeitliche Entwicklung einer allgemeinen Bilanzgröße ϕ in ei- nem Bilanzraum mit einer Transportbilanz beschreiben. Danach ergibt sich die zeitli- che Änderung einer Bilanzgröße aus der Summe der resultierenden molekularen (q_mol) und resultierenden konvektiven (q_kon) Ströme sowie der Quell- (q^_quelle) und Übergangsterme (hier der Einfachheit halber weggelassen).

.

mol kon

. quelle

t q



   



q. q (3.4)

Da bei den hier betrachteten rein diffusiven Transportvorgängen per se keine Konvek- tion auftritt, vereinfacht sich (3.4) zu:

mol

. .

quelle

t q



  

 q (3.5)

Theoretische Grundlagen der Diffusion und Sorption 18

Bei Betrachtung eines makroskopischen Bilanzgebietes müssen der Quellterm und der Term für die zeitliche Änderung von über das Volumen des Gebietes integriert wer- den. Die ein- und austretenden molekularen Ströme werden jedoch über die Fläche integriert, über die sie mit dem Bilanzgebiet kommunizieren. Dieses Flächenintegral kann mit Hilfe des gaußschen Integralsatzes in ein Volumenintegral überführt wer- den. Es ist zu beachten, dass die auf Grund der Definition des Normalenvektors eintre- tenden Ströme ein negatives Vorzeichen bekommen. Es ergeben sich somit für das makroskopische Bilanzgebiet folgende Gleichungen (Klöden, 2005):

mol quelle mol quelle

. . . .

dV dA q dV dV q dV

t



        





 



mol quelle

. .

d 0

q V

t



      

  

 



Gleichung (3.7) kann nur dann für jedes beliebige Bilanzgebiet gültig sein, wenn sich der Integrand zu null ergibt. Unter der Annahme, dass die molekularen Ströme über das 1. Fick’sche Gesetz beschrieben werden, ergibt sich die Änderung der Bilanzgröße (hier: Spezieskonzentration c) zu:

( ) ._quelle

c D c q

t

     

 (3.8)

Sind in dem betrachteten Bilanzgebiet keine Quellen oder Senken vorhanden reduziert sich (3.8) zum klassischen 2. Fick’schen Gesetz für Speziestransport im freien Medium (ohne Konvektion, Quellen/Senken sowie Übergangsterme):





c c

t 

  

 (3.9)

3.1.1.2 Anisotropes Medium

Für den Fall eines anisotropen Mediums wird der Diffusionskoeffizient D zu einem Tensor. Bei einem zweidimensionalen Modell gilt:

xx xy

yx yy

D D

D D

 

  

 

D (3.10)

Die Elemente dij des Tensors stehen für Diffusionsströme in Richtung i bei einem an- liegenden Gradienten in Richtung j. Bei der Verwendung eines dreidimensionalen Modells hat der Tensor die Form:

yy yz

xy xx xz

yx

zx zy zz

D D D

D D D

D D D

 

 

  

 

 

D (3.11)

Opalinuston mit seinem großen Anteil an Schichtsilikaten ist ein anisotropes Material (Van Loon et al., 2004b). Es wird üblicherweise mit einem diagonalen¹ (3x3) Diffusi- onstensor modelliert, wobei zwei der drei Diagonalelemente identische Werte anneh- men, nämlich die beiden Raumrichtungen parallel zur Schichtung (Samper et al. 2006).

Wird z.B. Dxx = Dzz gesetzt (Gleichung (3.12)), dann sagt man, dass eine Anisotropie in y-Richtung vorliegt. Als Veranschaulichung soll Abbildung 3 dienen.

0 0

0 0

0 0

xx

xx yy

D D

D

 

 

  

 

 

D (3.12)

Wird (3.12) in (3.9) eingesetzt und gilt, dass die Materialeigenschaften innerhalb jeder Raumrichtung homogen sind, ergibt sich für die dreidimensionale Diffusion in einem anisotropen, geschichteten Medium (hier: Opalinuston mit Anisotropie in y-Richtung) folgendes Gleichungssystem:

2 2 2

2 2 2

· _yy· ·

x x

x x y x

c D c D c D c

t z

  

 

   



 (3.13)

Abbildung 3: Struktur eines feinkörnigen, silikatischen Sedimentgesteins (A) während der Sedimentation und (B) nach der Kompaktierung (bevorzugte Ausrichtung der Tonplättchen senkrecht zur Belastung). (C) Diffusion senkrecht und parallel zur Struktur (C) und (D) Skizze der Diffusionsprozesse in einer perfekt geschichteten Probe (Van Loon et al., 2004b).

1 In diesem Fall muss das verwendete Koordinatensystem so gedreht werden, dass seine Achsen mit den Hauptrichtungen des Diffusionstensors übereinstimmen.

Theoretische Grundlagen der Diffusion und Sorption 20

3.1.2 Diffusion in porösen Medien

Bei der Modellierung der Diffusion in Opalinuston muss neben seiner Anisotropie auch beachtet werden, dass es sich um ein poröses Medium handelt (andere Möglich- keiten wären: Diffusion in freiem Medium (z.B. Wasser) oder Diffusion in doppelt po- rösem Medium (frei und porös)). Die Vorgehensweise zur Modellierung eines porösen Mediums im Allgemeinen wird im Folgenden beschrieben.

Die Porosität eines Festkörpers ε ist eine dimensionslose Kennzahl, die aus dem Ver- hältnis von Hohlraumvolumen zu Gesamtvolumen gebildet wird:

H ges

V

 V (3.14)

mit VH als Hohlraumvolumen des Gesteins und Vges als Gesamtvolumen.

Für Transportrechnungen ist jedoch als Kenngröße die effektive oder transportwirk- same Porosität εt des Gesteins interessanter. Sie kennzeichnet den transportwirksa- men Anteil der Gesamtporosität, welcher von einem Tracer durchflossen werden kann. Geschlossene Poren, also Poren ohne Verbindung zum restlichen Porensystem und solche, die auf Grund ihres Durchmessers nicht für die diffundierende Spezies zu- gänglich sind, gehen nicht mit in die effektive Porosität ein. Des Weiteren gibt es auch dead-end Poren. Diese gehen nicht durch das gesamte Gestein. Somit kann ein Tracer in solche Poren zwar ein- oder ausdiffundieren, aber in ihnen nicht das Gestein durchqueren. In Materialien mit negativer Oberflächenladung, wie es zum Beispiel bei Tonen der Fall ist, ist die effektive Porosität für Anionen kleiner als für Kationen, da Anionen von der negativ geladenen Oberfläche abgestoßen werden (Anionenaus- schlusseffekt).

Weitere Eigenschaften von natürlichem Gesteinsmaterial, die einen Einfluss auf den Transport von Tracern haben, sind z.B. die Konstriktivität und Tortuosität des Poren- raums.

Die Tortuosität τ dient als dimensionslose Kennzahl für die Wegverlängerung, die durch die Gewundenheit der Poren entsteht. Sie berechnet sich aus dem Verhältnis von mittlerer effektiver Weglänge durch den Porenraum leff zur eigentlichen Di- cke/Ausdehnung des Bilanzraums l, also der kürzesten Verbindung (Nakashima 1995):

leff

  l (3.15)

Auch die Konstriktivität δ ist eine dimensionslose Kennzahl. Je größer der Wert der Konstriktivität ist, desto mehr Widerstand erfährt die Spezies beim Transport durch

den Porenraum. Dieser erhöhte Widerstand entsteht durch das Anwachsen der Visko- sität des Lösungsmittels. Als Ursache wird die größere Nähe zur Porenwand angege- ben (Cussler, 2009). Es kommt zu einer Verringerung von De und damit zu einer lang- sameren Diffusion. Die Konstriktivität hängt vom Verhältnis des Teilchendurchmes- sers zum Porendurchmesser ab, welches _p genannt wird:

Spezies p

Pore

d

  d (3.16)

λp ist per Definition kleiner als 1 und beschreibt die Zugänglichkeit von Poren für ge- löste Spezies. In (Grathwohl, 1998) finden sich diverse empirische Gleichungen, die den funktionalen Zusammenhang zwischen δ und _p beschreiben, zum Beispiel auch die von (Satterfield & Colton, 1973):

exp( 4.6· p)

    (3.17)

Abbildung 4 veranschaulicht die Kennzahlen Tortuosität und Konstriktivität.

Abbildung 4: Schematische Darstellung des Einflusses von Konstriktivität und Tortuosität auf die Diffusion (Frick, 2003) in Van Loon & Soler (2004a). Der Porenraum ist schwarz darge- stellt, die umgebende Gesteinsmatrix gemustert.

Es nun somit möglich, den Einfluss eines porösen Materials auf die Diffusion mit Hilfe der obigen Kennzahlen zu berücksichtigen.

e aq t2

· ·

D D  

  (3.18)

Daq ist der Diffusionskoeffizient der jeweils modellierten chemischen Spezies in Was- ser. Gelegentlich werden die Porosität _t, Konstriktivität δ und Tortuosität τ auch zu einem Geometriefaktor G zusammengefasst (Van Loon et al., 2004a). Dies ist insofern

Theoretische Grundlagen der Diffusion und Sorption 22

gerechtfertigt, da sich die einzelnen Beträge zum effektiven Diffusionkoeffizienten nicht immer genau aufteilen lassen:

e aq·

D D G (3.19)

Durch Einsetzen von (3.18) für D in (3.1) erhält man das 1. Fick’sche Gesetz für Diffu- sion in porösen Medien ohne Sorption:

e· c

 D 

j (3.20)

Wird (3.18) für D in (3.9) eingesetzt, ist zu beachten, dass die Herleitung des 2. Fick’schen Gesetzes dort für das freie Medium erfolgte. Für ein poröses Medium muss das Volumen, über welches integriert wird, noch über die Porosität korrigiert werden, da das Fluid nicht mehr den gesamten Bilanzraum füllt:





t· c D · c

 ^t   

 (3.21)

Falls reaktiver Transport in einem natürlichen Gestein modelliert werden soll, muss die Gleichung (3.21) analog (3.8) um einen Quell- oder Senkenterm erweitert werden.

Im Rahmen der vorliegenden Arbeit wird als mögliche Reaktion die Sorption der Kon- taminanten an die umgebenden Mineralphasen betrachtet. Auf die Grundlagen der Sorption wird im folgenden Abschnitt eingegangen.

3.2 Sorptionsisothermen

3.2.1 Grundlagen der Sorption

Im Allgemeinen beschreibt der Begriff Sorption den Vorgang der Anlagerung von flüssigen oder gasförmigen Teilchen an eine Flüssig- oder Festphase. Der entgegenge- setzte Vorgang wird als Desorption bezeichnet. Die Anlagerung der Teilchen direkt an einer Oberfläche, zum Beispiel eines Feststoffes, wird spezieller als Adsorption be- zeichnet. Die Aufnahme von Teilchen durch diffusiven Transport in das Innere einer Phase wird als Absorption bezeichnet. Merkel und Planer-Friedrich (2008) bezeichnen diese Prozesse auch als Oberflächensorption (Adsorption) und Matrixsorption (Ab- sorption, Aufnahme von Teilchen in das Innere einer Gesteinsmatrix). Die stoffauf- nehmende Phase wird als Sorbens, die sich potentiell anlagernden Teilchen als Sorptiv und die Kombination aus angelagertem Sorptiv und Sorbens als Sorbat bezeichnet. Für das bessere Verständnis der Prozesse und Begriffe soll Abbildung 5 dienen.

Abbildung 5: Prozesse und Grundbegriffe der Sorption nach (Kümmel und Worch 1990).

Sorptionsprozesse werden häufig mit mathematischen Modellen beschrieben, die als Sorptionsisothermen bekannt sind. Sie werden in der Literatur als Isotherme bezeich- net, da die Messungen für die Beschreibung des Gleichgewichts bei konstanter Tem- peratur durchgeführt werden. Im Folgenden wird auf zwei einfache Isothermen einge- gangen, die häufig zur Beschreibung von Sorptionsprozessen in Transportbilanzen eingesetzt werden (Quell-/Senkenterm).

Das Verhältnis aus sorbiertem (fixiertem, immobilen) und unsorbiertem (frei, echt ge- löstem oder echt gasförmigem) Anteil einer Komponente bei Gleichgewichtsbedin- gungen stellt den sogenannten Verteilungskoeffizienten, oder Kd-Wert (Kd=cs/c), dar.

Dieser wird oftmals in m3/kg angegeben.

3.2.2 Lineare (Henry-)Isotherme

Der einfachste Fall einer Isotherme ist die Henry-Isotherme, die direkt aus der Defini- tion des Kd-Wertes hervorgeht. Bei ihr wird das Sorptionsgleichgewicht mit einem einfachen linearen Modell beschrieben:

d

s ·

c K c (3.22)

Dabei ist cs in mol/kg die Menge an angelagertem Sorptiv auf der Oberfläche des Sor- bens (Beladung) und c ist die sich einstellende Gleichgewichtskonzentration des Sorp- tivs in der Lösung. Die Henry-Isotherme hat den Nachteil, dass mit diesem linearen Ansatz keine Sättigungsbeladung beschrieben werden kann.

Neben dieser Isotherme zur einfachen empirischen Beschreibung von Sorptionspro- zessen an Oberflächen gibt es eine Reihe weiterer, auch physikalisch-chemischer Mo- dellansätze, zum Beispiel die Freundlich- und die Langmuir-Isotherme, das BET- Modell (Brunauer-Emmett-Teller) oder die Gruppe der Oberflächenkomplexierungs- modelle. Ein Überblick zu diesen Ansätzen ist in Merkel und Planer-Friedrich (2008) zu finden, sie werden in der vorliegenden Arbeit jedoch nicht verwendet.

Theoretische Grundlagen der Diffusion und Sorption 24

3.3 Diffusion unter Berücksichtigung von Sorption

Beide in Kapitel 3.2 beschriebenen Sorptionsansätze können über den Quell-/Senkenterm in die Transportmodellierung integriert werden. Gleichung (3.21) wird dafür wie folgt erweitert (Grathwohl, 1998; Shackelford & Daniel, 1991):

e

t s

( ) b c

c D c

t t

 ^      ^

  (3.23)

b

t s

( e ) c

c D c c

t c t

 ^      ^{ }

   (3.24)

Die Dichte ρb wird in diesen Gleichungen eingeführt, damit die Konzentration cs in der üblichen Einheit molSpezies/kgGestein angegeben werden kann (Shackelford 1991).

Für den Term c^s c



 wird jetzt der jeweilige Sorptionsmechanismus eingesetzt. Als Bei- spiel wird hier auf den am häufigsten verwendeten Fall der Henry-Isotherme einge- gangen:

d

s · dcs d

c K K

c d

  c  (3.25)

b d

t e

( K ) c (D c)

   ^t    

 (3.26)





e b

( ) mit ·

c D c

t K

^        

 (3.27)

a e

· ( ) mit Da D

c D c

t 

    

 (3.28)

Kd in kg/m3, ρb in kg/m3 ist die Bulkdichte des Materials. α ist der dimensionslose Ge- steins-Kapazitätsfaktor (engl. rock capacity factor), Da in m2/s ist der scheinbare (engl.

apparent) Diffusionskoeffizient (Da = De/α). Für einen konservativen Tracer, also für Kd = 0, wird aus Gleichung (3.26) wieder (3.21).

3.4 Notwendigkeit der Transportparameterschätzung mittels numerischer Simulation

Mit Gleichung (3.26) bzw. (3.28) können transiente Diffusionsstudien in porösen Mate- rialien simuliert werden. Zum Lösen der Modellgleichung sind noch Anfangs- und Randbedingungen entsprechend den gewählten experimentellen Bedingungen zu de-

finieren. Das daraus resultierende Anfangsrandwertproblem ist jedoch nicht in jedem Fall analytisch lösbar.

Für eine der experimentellen Diffusionsstudien, wie sie später in Kapitel 4.1 ausführ- lich beschrieben wird, gibt es eine analytische Lösung. Es wird eindimensionale, isotrope Diffusion in einer Probe der Dicke d modelliert, die anfänglich frei von Tracer ist. An beiden Seiten der Probe sind jeweils Reservoire mit konstanter Konzentration vorhanden. Es ergibt sich somit folgendes Anfangsrandwertproblem:

· c ( ·e )

D c

 ^t   

 (3.29)

( , ) 0;c x t  x[0, ];d t 0 (3.30)

 ₀ 

(0, ) .; 0

c t c const t (3.31)

 

( , ) 0; 0

c d t t (3.32)

Die analytische Lösung dieses Problems ist bekannt (Crank, 1975; Van Loon & Soler 2004a; Jakob et al., 1999):

2 2

n

0 2e 2 2 2

n 1

· ·

1 2 ( 1)

· · · · ·ex

, ) 6 ·

( p

·

D D ne

d c t

t n

m A d t

d   d 

 





     

  

 



m ist die kumulierte Speziesmasse, die bis zum Zeitpunkt t durch die Fläche A in das Reservoir mit der niedrigen Konzentration diffundiert ist. Gleichung (3.33) wurde zwar für die Randbedingung c(d,t) = 0 ermittelt, ist aber auch gültig, so lange c(d,t) << c0 erfüllt ist (Van Loon & Soler, 2004a).

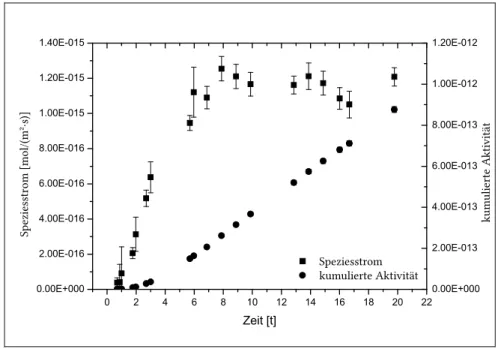
Für zunehmende Zeitdauern t geht der Exponentialterm in (3.33) gegen null und Glei- chung (3.33) kann folgendermaßen beschrieben werden:

0 2e

0 e 0

2

1 2

( , ) · · · · 1 6

· · · · 6

·

m d t A d c D t d

A d c D t A d c d

x t x





 

   

 

 

(3.34)

Durch Regression dieser linearen Gleichung an Messdaten der kumulierten Masse im Reservoir mit niedriger Konzentration können der effektive Diffusionskoeffizient De

und der Felsfaktor α der Probe bestimmt werden. Explizit gilt bei konservativen Tra- cern (Kd=0), dass α gleich der transportwirksamen Porosität der Probe ist (Gleichung (3.27) und

Theoretische Grundlagen der Diffusion und Sorption 26

e 1 0

·

·

D x d

 A c (3.35)

sowie

   ²

0

6·

· · x

A d c (3.36)

Eine Parameterbestimmung mit Hilfe von Gleichung (3.34) ist jedoch nur für die gege- benen Anfangs- und Randbedingungen möglich, sowie dann, wenn es zu einem Durchbruch der Spezies durch die Probe und dem Erreichen der Phase kam, in dem die Masse im Reservoir mit der niedrigen Konzentration linear zunimmt. Für komplizier- tere Geometrien oder Anfangs- und Randbedingungen muss Gleichung (3.28) nume- risch – also mittels Computersimulation - gelöst werden. Zur Lösung von partiellen Differentialgleichungen ist zum Beispiel die Methode der finiten Elemente (FEM) ge- eignet. Bei der Parameterschätzung mit partiellen Differentialgleichungen resultieren unter Umständen nichtlineare Anpassungsprobleme. Diese bedürfen anderer Metho- den als der linearen Regression. Auf lineare und nichtlineare Anpassungsprobleme sowie geeignete Lösungsalgorithmen für diese Aufgaben wird im nachfolgenden Kapi- tel eingegangen.

4 Theoretische Grundlagen der Parameterschätzung

4.1 Einleitung

Die folgenden Ausführungen zur Parameterschätzung beziehen sich, falls nicht aus- drücklich anders angegeben, auf die Quellen Aster et al. (2005) und Madsen et al.

(2004).

In vielen wissenschaftlichen Aufgabenstellungen gibt es den Wunsch oder es ergibt sich die Notwendigkeit einen experimentell ermittelten Messdatensatz b mit einem physikalischen oder chemischen Modell A zu beschreiben:

( )A x b (4.1)

Sind A und x bekannt und möchte man b ermitteln, spricht man von einem direkten oder Vorwärtsproblem. Dahingegen spricht man von Systemidentifikation, wenn b und x bekannt sind, aber A gesucht wird. Nachfolgend werden kurz die Grundlagen des dritten Falls, der Parameterschätzung (inverses Problem), behandelt. In diesem Fall sind b und A bekannt und man möchte die (Modell-)Parameter x ermitteln (Aster et al., 2005).

Würden die Messdaten aus einem Experiment ohne Fehlerquellen stammen, könnte Gleichung (4.1) exakt gelöst werden und man würde als Lösung die Parameter xperf

erhalten:

perf ( perf)

b A x (4.2)

b b perf  (4.3)

In realen Experimenten sind Messdaten jedoch mit Fehlern η behaftet, sodass nicht alle ermittelten Messdaten mit den durch das Modell vorhergesagten Werten überein- stimmen. Die Parameter b werden unter diesen Bedingungen so ermittelt, dass das Modell möglichst nah an allen Datenpunkten liegt. Sie minimieren dann ein vorher bestimmtes Maß der Abweichung r zwischen Modell und Daten (Ausgleichsproblem):

( )r b A x  (4.4)

r wird auch Residuum genannt. Im Folgenden wird auf die Methode der kleinsten Quadrate eingegangen, in welcher die 2-Norm der Residuen minimiert wird. Die 2- Norm oder euklidische Norm (||.||2) ist die Wurzel aus der Summe der Quadrate von r.

Theoretische Grundlagen der Parameterschätzung 28

Die Minimierung der 2-Norm ist wahrscheinlich der häufigste Fall in der Praxis, daher beschränken sich die folgenden Ausführungen auf diese Wahl der Norm.

4.2 Methode der kleinsten Quadrate

4.2.1 Lineare Ausgleichsprobleme

Eine der bekanntesten Formen des linearen Ausgleichproblems ist das Fitten eines Da- tensatzes mit k Messpunkten m(t) mittels der Geraden m = x1·t-x2 (siehe z.B. Glei- chung (3.34)). Daraus ergibt sich ein lineares Gleichungssystem mit k Gleichungen.

Die Anzahl der Modellparameter beträgt hier n = 2.

Gleichung (4.1) kann für ein allgemeines Ausgleichsproblem auch in Matrixform ge- schrieben werden:

b = Ax (4.5)

Somit ergeben sich die Residuen zu:

i i ij j

r  b A x

r = b - Ax (4.6)

wobei ri das i-te Residuum der 1 ≤ i ≤ k Messpunkte und xj der j-te Modellparameter ist. Die Summe der Fehlerquadrate ist dann definiert als:

k 2 T

i i=1

( ) 1· ( ( )) 1 ( ) 2

2 ( )

F x 



mit r =(r1(x), r2(x), …, rk(x))^T. Der Vorfaktor ½ wurde eingeführt, um die späteren Dar- stellungen übersichtlicher zu gestalten. Durch ihn entfällt der Faktor 2, der sich bei der Ableitung von (ri(x))2 ergibt.

Es sollen jetzt die Parameter x*j gefunden werden, mit denen die Summe der Fehler- quadrate minimal wird.

 

=argmin_x

x* F(x) (4.8)

Ist x* ein Extremum von F(x), dann gilt für den Gradienten an dieser Stelle:

F(x*) F'(x*) 0 (4.9)

Neben dieser notwendigen Bedingung muss der ermittelte Extrempunkt noch die hin- reichende Bedingung, ''( *) 0F x  , erfüllen, damit er ein Minimum ist. Dies ist gewähr- leistet, wenn ''( *)F x positiv definit ist (Madsen et al., 2004).

Die partielle Ableitung von Gleichung (4.7) nach xj unter Anwendung der Kettenregel ist:

k !

i

i=

i i

j 1 j

( ( )

) )·

( 0

F x r x

x r x x

 

 





Unter Zuhilfenahme der folgendermaßen definierten Jacobi-Matrix:

1 1

1 j

i i

1 j

( ) ( )

( )

( ) ( )

r x r x

x x

x

r x r x

x x

 

 

   

 

 

  

   

 

J



  



(4.11)

kann die 1. Ableitung von F(x) wie folgt geschrieben werden als:

T T

( )x  ( ) ( )x x  ( )x ( )x

F J r r r (4.12)

Für den linearen Fall gilt:

i( )

ij j

r x A

x

   

 J = A (4.13)

und somit ergibt sich nach Einsetzen von (4.13) und (4.6) in (4.12) für die optimal ge- schätzten Parameterwerte:

0 ( *)

*

T

T T

 

 A b - Ax

A Ax A b (4.14)

Gleichung (4.14) wird auch als Normalengleichung bezeichnet. Die in Gleichung (4.8) gesuchten Parameter x* sind die Lösung der Normalengleichung:

 

* ^{T  T}

x A A A b (4.15)

Die Parameter x1 und x2 aus dem einführenden Beispiel (m=x1·t+x2) ergeben sich also über:

    

    

 

   

    

  

 

  

1 1

1 2

1

1

·

k k

x x

m t

m t

(4.16)





 







1 1



1

2

·(

( ) )

( )

k

i

i k

i

i i

m

t t m

x

t t

(4.17)

Theoretische Grundlagen der Parameterschätzung 30

2   1·

x m x t (4.18)

Wird die Regression bei der Auswertung von Gleichung (3.34) analog der oben be- schriebenen Vorgehensweise durchgeführt, handelt es sich um eine ungewichtete Regression. Sind für die einzelnen Messungen Fehler σ bekannt, kann das jeweils zu- gehörige Residuum mit diesem Fehler gewichtet werden:

2 1 2

· 1 (

( ) 1 ( ))

2

k i

i i

F x r x

 





Dadurch erhalten Messungen mit einem kleinen Fehler ein größeres Gewicht als sol- che mit einem großen Fehler.

4.2.2 Nichtlineare Ausgleichsprobleme

Für den Fall des nichtlinearen Ausgleichsproblems und ausgehend von Gleichung (4.12):

( )Fx = F'( )x  r( ) ( )x ^Tr x (4.20)

ist zu beachten, dass hier ∇r(x) nicht –A ergibt, sondern tatsächlich noch von x ab- hängt. Wird Gleichung (4.20) erneut nach den Parametern xj abgeleitet, ergibt sich die Hesse-Matrix der Funktion F wie folgt:

1

2 ( ) ( ) ^m ( ) 2 ( )

i T

i i

x

x x x r x r x



 F( ) F''( ) ^r ^r 



Bei Ausgleichsproblemen mit kleinen Residuen ri(x) kann Gleichung (4.21) folgender- maßen vereinfacht werden (Aster et al., 2005):

2 (x) ( )x ^T (x)

 F r r (4.22)

Somit kann die Hesse-Matrix bei guter Übereinstimmung von Modell und Messdaten nur mit Hilfe der 1. Ableitung approximiert werden. Diese Annahme nutzt zum Bei- spiel der Gauss-Newton-Algorithmus, auf den u. a. im nachfolgenden Abschnitt ge- nauer eingegangen wird.

4.3 Numerische Optimierungsalgorithmen

4.3.1 Verfahren des steilsten Abstiegs

Bei Gradientenverfahren werden ausgehend von einer Anfangsnährung für x* jeweils Schritte in negativer Gradientenrichtung, der Richtung des steilsten Abstiegs der Ziel-

funktion, durchgeführt, bis sich der Wert der Zielfunktion nicht mehr verbessert, d.h.

für den Fall eines Minimierungsproblems, dass sich die Zielfunktion nicht mehr ver- ringert. Die Iterationsvorschrift für eine gradienten-basierte Optimierung ist:

1 ·

i_  i  x

x x F( ) (4.23)

mit einem Schrittweitenparameter α, welcher so gewählt wird, dass er folgende Be- dingung erfüllt:

argmin { (_ F _i · ( ))}x

  x  F (4.24)

Methoden zur genauen Wahl von α werden in (Frandsen et al., 2004) beschrieben. Es bieten sich Methoden der eindimensionalen Suche an. In die Gradientenrichtung er- folgt ein Schritt, der so groß ist, dass die Zielfunktion in dieser Richtung möglichst minimal wird. Der Schrittweitenparameter α muss in jeder Iteration neu bestimmt werden.

Nach Frandsen (2004) und Madsen (2004) ist ein großer Vorteil von Gradientenverfah- ren ihre gute Leistungsfähigkeit für den Fall, dass die gewählte Anfangsnährung von x* weit vom gesuchten Extrempunkt entfernt ist. Ihr Nachteil ist die teilweise sehr langsame (meist lineare) Konvergenz in der Nähe der Lösung.

4.3.2 Gauss-Newton-Algorithmus

Der Newton-Algorithmus in der Optimierung (nicht zu verwechseln mit dem klassi- schen Newton-Algorithums für das Ermitteln einer Nullstelle) erzeugt, genau wie das Gradientenverfahren, eine Reihe von Parameterwerten x0, x1, …, x* für die gilt:

( *) 0x 

F' (iterative Methoden). Es handelt sich bei dem ermittelten x* also um die Nährung für ein Minimum der Funktion F. Zur Bestimmung dieses Minimums wird für den Gradienten von F um die Entwicklungsstelle x0 eine Taylorentwicklung durchgeführt, welche nach dem quadratischen Term abgebrochen wird (Madsen et al., 2004):

2

0 ) 0) 0

(x x (x ( )x 0

F   F  F  x (4.25)

2

0 ( 0

( )x   x )

 F x F (4.26)

Aus (4.26) ergibt sich die Iterationsvorschrift:

1 2

( ) ( )

n

n n

xn

x





 

x x

F

F (4.27)

Theoretische Grundlagen der Parameterschätzung 32

Der Gauss-Newton-Algorithmus ist ein spezialisierter Algorithmus für nichtlineare Anpassungsprobleme. Er nutzt die Approximation der zweiten Ableitung mittels Glei- chung (4.22):

 

1 ( )^T ( ) ( ) ( )^T

n_  n   xn  xn ^  xn xn

x x r r r r (4.28)

Das Gauss-Newton-Verfahren benötigt somit im Gegensatz zum Newton-Verfahren für die Ermittlung des Minimums nicht die zweite Ableitung der Funktion sondern nur noch die erste Ableitung. Jedoch kann die Verwendung der Nährung (4.22) bei Anpassungsproblemen, bei denen die Residuen nicht klein sind, zu langsamer Konver- genz führen.

4.3.3 Levenberg-Marquardt-Algorithmus

Levenberg (1944) und Marquardt (1963) schlagen eine Kombination aus Gradienten- verfahren und Gauss-Newton-Verfahren vor. Dazu modifizierten sie Gleichung (4.28) folgendermaßen (Aster et al., 2005; Frandsen et al., 2004; Madsen et al., 2004):

1

1 _n ( ( )^T ( ) _LM ) ( ) ( )^T _n

n_    xn  xn  ^ r xn r x

x x r r I (4.29)

mit dem Dämpfungsfaktor _LM und der Einheitsmatrix I. Dieser kann als Approxima- tion des Summenterms in Gleichung (4.21) angesehen werden. Für (sehr) große _LM erfolgt beim Levenberg-Marquardt-Algorithmus ein kurzer Suchschritt in Richtung des steilsten Abstiegs. Dahingegen wird für kleine _LM ein Suchschritt entsprechend dem Gauss-Newton-Verfahren durchgeführt. Dies ist gut für Iterationen in der Nähe der Lösung, da das Gauss-Newton-Verfahren eine schnellere Konvergenz bietet als das Gradientenverfahren. Des Weiteren wird für positiv gewählte _LM sichergestellt, dass der Klammerausdruck mit _LMI positiv definit ist und somit durch den Levenberg- Marquardt-Algorithmus ein Suchschritt in Richtung fallender Zielfunktionswerte durchgeführt wird.

Für die praktische Umsetzung des Levenberg-Marquardt-Algorithmus spielt die Wahl des _LM eine entscheidende Rolle und stellt zugleich eine Herausforderung dar. Es wurden verschiedene Strategien zur Wahl des Dämpfungsfaktors entwickelt. Bezüg- lich der genauen Umsetzung dieser Strategien wird auf die Literatur verwiesen (Aster et al., 2005; Frandsen et al., 2004; Madsen et al., 2004).

Der Levenberg-Marquardt-Algorithmus für die Minimierung von Fehlerquadratsum- men ist im Optimierungsmodul von COMSOL Multiphysics implementiert und wurde für die Parameterschätzung der in Kapitel 5 beschriebenen Experimente verwendet.

4.4 Regularisierungsmethoden

4.4.1 Einführung zu schlecht-gestellten Problemen

Bei den in Abschnitt 4.1 beschriebenen inversen Problemen handelt es sich oftmals um sogenannte schlecht-gestellte Probleme (engl. ill-posed problems) (Engl et al., 1996;

Hansen, 1992; Aster et al., 2005). Die Unterteilung von Problemen in korrekt-gestellte (well-posed) und schlecht-gestellte Probleme geht auf den französischen Mathemati- ker Jacques Hadamard zurück. Laut seiner Definition muss ein korrekt-gestelltes Problem die folgenden drei Anforderungen erfüllen (Engl et al., 1996; Aster et al., 2005):

(1) Das Problem muss für alle zulässigen Daten eine Lösung besitzen (Existenz).

(2) Die Lösung des Problems muss eindeutig sein (Eindeutigkeit).

(3) Die Lösung muss stetig von den Daten abhängen (Stabilität).

Wird eine dieser Anforderungen nicht erfüllt, handelt es sich um ein schlecht- gestelltes Problem. Vor allem Forderung (3) hat bei inversen Problemen eine große Bedeutung. Aus ihr ergibt sich, dass kleine Änderungen in den Daten nur kleine Än- derungen in der Lösung verursachen dürfen. Dies ist wichtig, da bei inversen Prob- lemstellungen oft Messdaten verwendet werden, die naturgemäß fehlerbehaftet sind.

In der Praxis wird jedoch gerade diese Anforderung (3) oftmals nicht erfüllt mit der Folge, dass kleine Fehler in den Daten (sehr) große Änderungen der Lösung verursa- chen.

Das mathematische Problem, welches vielen schlecht-gestellten Problemen zugrunde liegt, ist eine Fredholm’sches Integralgleichung 1. Art:

( ) ( , ) ( )d

d

c

b s 



Dieses kontinuierliche inverse Problem kann durch Diskretisierung in das schon be- kannte lineare Gleichungssystem überführt werden (vergleiche auch Gleichung (5.5)) (Aster et al., 2005):

b = Ax (4.31)

Der Tensor b, welcher die Messdaten enthält, hat dann nur noch eine endliche Anzahl von Einträgen. Wenn der Tensor A eine große Konditionszahl aufweist, also kleine Änderungen in den Daten große Änderungen in der Lösung verursachen können,

Theoretische Grundlagen der Parameterschätzung 34

dann handelt es sich bei (4.31) um ein schlecht-gestelltes Problem. In der Literatur werden diese Probleme auch als discrete ill-posed problems (DIP) bezeichnet.

Eine Möglichkeit die Auswirkungen von großen Konditionszahlen zu umgehen, ist das Einbeziehen von zusätzlichen Informationen in den Lösungsprozess. Oftmals soll die ermittelte Lösung des Problems gewisse Anforderungen bezüglich ihrer „Glätte“ erfül- len. Dabei wird das ursprüngliche Problem durch ein neues (ähnliches) Problem er- setzt. Solche Methoden werden Regularisierungsmethoden genannt. Auf einen ihrer bekanntesten Vertreter, die Tikhonov-Regularisierung, wird im folgenden Abschnitt kurz eingegangen.

4.4.2 Tikhonov-Regularisierung

Bei der Tikhonov-Regularisierung werden die im vorherigen Abschnitt beschriebenen a priori Informationen zur „Glätte“ oder Größe der gesuchten Lösung berücksichtigt (Aster et al., 2005; Hansen, 1998; Engl et al., 1996). Da die Informationen über einen Regularisierungsterm direkt mit in die Zielfunktion integriert werden, zählt die Me- thode nach Tikhonov zu den direkten Regularisierungsmethoden. Sie hat die folgende allgemeine Form:





min ||Ax - b||  ||Lx|| (4.32)

mit  als Regularisierungsparameter, welcher der Wichtung zwischen der Minimie- rung des Regularisierungsterms ||Lx|| und der Minimierung der Residuen ||Ax-b|| dient und L als Tikhonov- oder roughening-Matrix.

Für den Fall das L der Einheitsmatrix entspricht, L = I, spricht man von einer Regula- risierung 0. Ordnung. Ist L eine Approximation der 1. Ableitung der Zielfunktion, L = L1, handelt es sich um eine Regularisierung 1. Ordnung und für den Fall, dass L die zweite Ableitung, L = L2, approximiert, handelt es sich um eine Tikhonov- Regularisierung 2. Ordnung. Die Verwendung des Terms ||L1x|| würde Lösungen be- vorzugen, die relativ flach sind (kleine erste Ableitung). Bei der Minimierung des Re- gularisierungsterms ||L2x|| werden Lösungen bestraft, die keine „glatte“ zweite Ablei- tung haben.

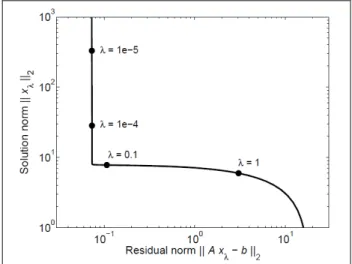
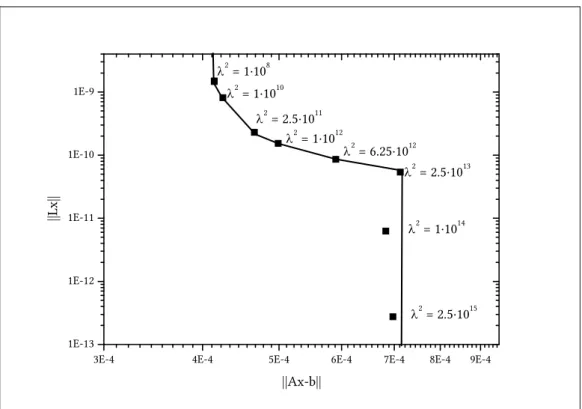
Neben der Wahl der Tikhonovmatrix L spielt in der Praxis die Wahl eines optimalen Regularisierungsfaktors  eine wichtige Rolle und stellt zugleich eine nicht triviale Aufgabe dar. Eine weitverbreitete Methode dazu ist die Wahl des Regularisierungspa- rameters über den L-Plot / die L-Kurve (Engl et al., 2005; Hansen, 1992; Hansen et al., 1993; Hansen, 1998). Sie ist nach ihrem charakteristischen L-förmigen Verlauf be-