Eine besondere Rolle sowohl in der linearen Algebra als auch der Analysis spielen lineare Abbildungen. Auf endlich erzeugten Vektorräumen hängen diese eng mit sogenannten Matrizen (rechteckige Zahlenschemata) zusammen. Um für den weiteren Verlauf dieses Kapitels eine Anschauung zu entwickeln, werden daher zunächst der Begriff der Matrix sowie grundlegende Matrix-Vektor Operationen eingeführt.
8.1 Lineare Gleichungssysteme und Matrizen
In vielen Anwendungen ist man an Lösungen von sogenanntenlinearen Gleichungssyste- men interessiert. Hierbei sucht man n Unbekannte die m lineare Bedingungen erfüllen.
Definition 8.1 (Lineares Gleichungssystem)
Für m, n2 N bezeichnet man für die n Unbekannten x1, x2, . . . , xn 2 K und die Werte b1, . . . , bm 2Kdie m Gleichungen
a11x1 + a12x2 +. . .+ a1nxn = b1
a21x1 + a22x2 +. . .+ a2nxn = b2
... ... ... ...
am1x1 + am2x2 +. . .+ amnxn = bm
als lineares Gleichungssystem. Die Zahlen aij 2 K (1 i m,1 j n) heißen Koeffizienten. Das Gleichungssystem lässt sich auch kompakt schreiben als
Xn
j=1
aijxj =bi, für i= 1, . . . , m.
Das obige Gleichungssystem möchte man in vielen Fällen kompakter (und damit über- sichtlicher) notieren. Wesentlich für ein Gleichungssystem sind die Koeffizienten und daher fasst man diese in einem Zahlenschema zusammen.
Definition 8.2 (Matrix)
Eine m⇥n Matrix A, m, n2 N, mit Einträgen aij 2K, 1 im, und 1 j n ist
ein rechteckiges Zahlenschema
A= (aij)m,ni,j=1 = 0 BB B@
a11 a12 . . . a1n
a21 a22 . . . a2n ... ... ... ...
am1 am2 . . . amn
1 CC CA.
Die Menge aller m⇥n Matrizen mit Einträgen aus K wird alsKm⇥n bezeichnet.
Um damit das obige Gleichungssystem kompakter notierien zu können, wird noch die Definitionen der Multiplikation einer Matrix mit einem Vektor benötigt.
Definition 8.3 (Matrix-Vektor-Multiplikation)
Zu einer Matrix A2Km⇥n und einem Vektor x2Kn ist das Matrix-Vektor-Produkt
·:Km⇥n⇥Kn !Km definiert durch
A·x= 0 BB B@
a11 a12 . . . a1n
a21 a22 . . . a2n ... ... ... ...
am1 am2 . . . amn
1 CC CA·
0 BB B@
x1
x2 ...
xn
1 CC CA:=
0 BB B@
a11·x1+a12·x2+. . .+a1n·xn
a21·x1+a22·x2+. . .+a2n·xn ...
am1·x1+am2·x2+. . .+amn·xn
1 CC CA
oder in Indexnotation
(A·x)i :=
Xn j=1
aijxj, für alle 1im.
Damit lässt sich ein lineares Gleichungssystem in Matrixschreibweise darstellen. Sei dazu A2Km⇥n und b 2Km. Gesucht ist dannx2Kn, so dass
A·x= 0 BB B@
a11x1 + a12x2 +. . .+ a1nxn a21x1 + a22x2 +. . .+ a2nxn
... ... ...
am1x1 + am2x2 +. . .+ amnxn
1 CC CA=
0 BB B@
b1 b2
...
bm
1 CC CA=b.
Beispiele 8.4 (i) A:= 2 2R1⇥1: A·x= (2)·(x1) = 2x1. (ii) A:= 3 4 2R2⇥1: A·x= 3 4 ·
✓x1
x2
◆
= 3x1+ 4x2. (iii) (Identität) A:=
✓1 0 0 1
◆
2R2⇥2:
A·x=
✓1 0 0 1
◆
·
✓x1
x2
◆
=
✓1·x1+ 0·x2
0·x1+ 1·x2
◆
=
✓x1
x2
◆
=x.
(iv) (Rotation um 90 ) A:=
✓0 1 1 0
◆
2R2⇥2: A·x=
✓0 1 1 0
◆
·
✓x1
x2
◆
=
✓0·x1 1·x2
1·x1+ 0·x2
◆
=
✓ x2
x1
◆ .
Die so definiert Abbildung besitzt interessante Eigenschaften.
Satz 8.5 (Linearität der Matrixmultiplikation)
Die Multiplikation einer MatrixA2Km⇥n mit einem Vektorx2Knist eine Abbildung A :Kn !Km,x7!A·x und besitzt die Eigenschaften
A·(x+y) =A·x+A·y, A·( x) = (A·x), für allex,y2Kn, 2K. Beweis. Beim direkten Nachrechnen kann man sich auf die i-te Zeile beschränken und findet
(A·(x+y))i = Xn
j=1
aij(xj +yj) = Xn
j=1
aijxj+ Xn
j=1
aijyj = (A·x)i+ (A·y)i
sowie
(A·( x))i = Xn j=1
aij( xj) =
Xn j=1
aijxj
!
= (A·x)i.
⇤ Für Matrizen lässt sich zudem eine Addition, eine Multiplikation mit Skalaren und eine Multiplikation mit Matrizen definieren.
Definition 8.6 (Matrix-Matrix-Operationen) Für A,B 2Km⇥n ist die (Matrix-)Addition definiert als
A+B= 0 BB B@
a11 a12 . . . a1n
a21 a22 . . . a2n ... ... ... ...
am1 am2 . . . amn
1 CC CA+
0 BB B@
b11 b12 . . . b1n
b21 b22 . . . b2n ... ... ... ...
bm1 bm2 . . . bmn
1 CC CA
= 0 BB B@
a11+b11 a12+b12 . . . a1n+b1n
a21+b21 a22+b22 . . . a2n+b2n
... ... ... ...
am1+bm1 am2+bm2 . . . amn+bmn
1 CC CA
und die Multiplikation mit einem Skalar 2K als A =
0 BB B@
a11 a12 . . . a1n
a21 a22 . . . a2n
... ... ... ...
am1 am2 . . . amn
1 CC CA=
0 BB B@
a11 a12 . . . a1n
a21 a22 . . . a2n
... ... ... ...
am1 am2 . . . amn
1 CC CA.
Für A 2 Km⇥n und B 2 Kn⇥r ist das Matrixprodukt eine Matrix C 2 Km⇥r gegeben durch
C=A·B, mit cik :=
Xn j=1
aijbjk für i = 1, . . . , mk = 1, . . . , r .
Im Spezialfallr = 1stimmt diese Definition mit der Matrix-Vektor-Multiplikation über- ein.
Definition 8.7 (Transponierte Matrix)
Die zuA2Km⇥n transponierte Matrix AT 2Kn⇥m ist definiert durch aTij :=aji für i = 1, . . . , n,j = 1, . . . , m .
Anschaulich gesprochen entspricht dies der Spiegelung an der Diagonalen (aii)max(n,m)i=1 der Matrix und diese fasst man einen Vektor x2Rn⇥1 als einspaltige Matrix x2Rn⇥1 auf, so ist diese Definition konsistent mit der Notation eines liegenden Vektors xT = (x1, . . . , xn).
Eine wichtige Matrix ist die sehr einfache Einheitsmatrix.
Definition 8.8 (Einheitsmatrix) Die Einheitsmatrix ist dien⇥n Matrix
1n:=
0 BB B@
1 0 . . . 0 0 1 . . . 0 ... ... ... ...
0 0 . . . 1 1 CC CA.
Für die Rechenregeln mit Matrizen findet man zudem folgende Äquivalenzen.
Satz 8.9 (Rechenregeln für Matrizen)
Seien A2Rm⇥n und B,C2Rn⇥r Matrizen sowie 2K. Dann gilt:
(i) A·(B+C) =A·B+A·C, (A+B)·C=A·C+B·C, (ii) A·(B·C) = (A·B)·C,
(iii) A·( B) = ( A)·B = (A·B), (iv) (A·B)T =BT ·AT,
(v) 1m·A=A·1n=A.
Im Allgemeinen gelten jedoch die folgenden Ungleichungen A·B 6=B·A und A·B6=AT ·BT
für beliebige MatrizenA,B, obwohl selbstverständlich für Spezialfälle Gleichheit vorlie- gen kann.
8.2 Lösungsmengen, Kern und Bild
Gleichungssysteme entstehen an vielen Stellen und für ihre Lösung ist ein verlässliches Verfahren wünschenswert.
Zum Beispiel führt die Berechnung von Schnittpunkten zwischen Ebenen im R3 auf solche Gleichungssysteme. Eine Ebene im R3 lässt sich über eine lineare Gleichung be- schreiben
{x2R3 | a1x1 +a2x2+a3x3 =b},
mit Koeffizienten ai 2 R, i = 1,2,3 und rechter Seite b 2 R. Um den Schnittpunkt dreier Ebenen im R3 zu berechnen, muss dementsprechend einx2R3 gefunden werden, so dass simultan die Ebenengleichung für alle drei erfüllt ist, d.h. es gilt
a11x1+a12x2+a13x3 =b1
a21x1+a22x2+a23x3 =b2
a31x1+a32x2+a33x3 =b3
oder kurz
A·x=b,
mit A= (aij)2R3⇥3 und x= (xi)2R3, b= (bi)2R3.
Eliminationsverfahren von Gauß
Es stellt sich nun die Frage, ob eine solche Matrixgleichung überhaupt eine Lösung besitzt und falls ja, ob die gefundene Lösung die einzige ist. Ein Allgemeines Verfahren zur Bestimmung der Lösungen eines solchen Gleichungssystem ist das Verfahren von Gauß.
Dabei formt man Matrix und rechte Seite geeignet um, so dass sich bei gleichbleibender Lösung eine Zeilenstufenform der Matrix ergibt, aus der man die Lösung durch einfaches Einsetzen ablesen kann.
Dies erklärt sich am besten durch ein Beispiel. Seien {x2R3 | 2x1+x2+ 3x3 = 8}, {x2R3 | 2x1+ 2x2+ 4x3 = 12}, {x2R3 | 4x1+ 4x2+ 6x3 = 14}
Ebenen im Raum, deren Schnittpunkt gesucht ist. Ausgehend von den drei Gleichungen 2x1 + x2 + 3x3 = 8 (i)
2x1 + 2x2 + 4x3 = 12 (ii) 4x1 + 4x2 + 6x3 = 14 (iii)
erhält man durch Addition des Vielfachen einer Gleichung zu den anderen zunächst 2x1 + x2 + 3x3 = 8 (i)
x2 + x3 = 4 (ii :=ii+ ( 1)·i) 6x2 + 12x3 = 30 (iii :=iii+ 2·i) und schließlich die sogenannte Zeilenstufenform
2x1 + x2 + 3x3 = 8 (i) x2 + x3 = 4 (ii)
6x3 = 6 (iii :=iii+ ( 6)·ii)
Nun lässt sich die Lösung direkt von unten nach oben ablesen. Denn durch einfaches Dividieren findet man aus (iii) nun zunächst x3 = 1. Einsetzen von x3 in (ii) und Umformen ergibt x2 = 3 und schließlich Einsetzen von x2 und x3 in (i) und Umformen x1 = 1.
Man rechnet zudem leicht nach, dass die Lösung xT = (1,3,1) des so umgeformten Gleichungssystem
Ae ·x= 0
@2 1 3 0 1 1 0 0 6
1 A·
0
@1 3 1
1 A=
0
@8 4 6
1 A=be auch die Lösung des ursprünglichen Gleichungssystem
A·x= 0
@ 2 1 3 2 2 4 4 4 6
1 A·
0
@1 3 1
1 A=
0
@8 12 14
1 A=b
ist. Dieses Vorgehen lässt sich auf beliebige MatrizenA 2Km⇥n anwenden und soll nun im Folgenden systematisch untersucht werden.
Definition 8.10 (Lösungsmenge)
Die Lösungsmenge eines linearen Gleichungssystems Ax=b ist gegeben durch L(A,b) :={x2Kn|Ax=b}.
Ist dieses Menge leer, so ist das Gleichungssystem nicht lösbar. Enthält sie genau einen Vektor, so ist dies eine eindeutige Lösung. Gibt es mehr als ein Element in der Lösungs- menge, so hat das Gleichungssystem mehr als einen Lösung.
Das Ziel des Algorithmus von Gauß ist es, diese Menge zu bestimmen. Dazu schreibt man das zu lösende Gleichungssystem oftmals der Einfachheit halber alserweiterte Ko- effizientenmatrix
(A|b) = 0 BB B@
a11 a12 . . . a1n b1
a21 a22 . . . a2n b2
... ... ... ... ...
am1 am2 . . . amn bm
1 CC CA.
Nun stellt man zunächst direkt fest, dass es Gleichungssysteme gibt, die sich besonders einfach lösen lassen. Diese haben die folgende Gestalt, bei der das untere Dreieck der Matrix nur aus Nullen besteht.
Definition 8.11 (Zeilenstufenform)
Eine Matrix A 2 Km⇥n besitzt Zeilenstufenform, wenn es einen Zahl r (0 r m) gibt, so dass die Zeilen folgende Form haben:
(i) In den Zeilen r+ 1, . . . , m sind alle Einträge Null.
(ii) In den Zeilen1, . . . , r sind nicht alle Einträge Null und die von Null verschiedenen Einträge mit kleinstem Spaltenindex ji := min{j|aij 6= 0} (sogenannte Pivots) erfüllen die Bedingung j1 < j2 < . . . < jr.
Die Matrix hat somit die Gestalt
A= 0 BB BB BB BB BB B@
0 . . . 0 a1,j1 ⇤ . . . ⇤ ⇤ . . . ⇤ . . . ⇤
0 . . . 0 a2,j2 ⇤ ⇤ . . . ⇤
0 . . . 0 a3,j3 ⇤ . . . ⇤
... ...
ar,jr ⇤ . . . ⇤
0 0 . . . 0
... ...
0 . . . 0 1 CC CC CC CC CC CA ,
wobei die Pivots ai,ji 6= 0 (1ir) nicht null sind, an mit ⇤gekennzeichneten Stellen sowohl von Null verschiedenen Einträge als auch Nullen stehen dürfen und unterhalb der eingezeichneten Linie nur Nullen stehen. Nun stellt man fest, dass sich die Lösungsmenge eines linearen Gleichungssystems in einer Zeilenstufenform direkt ermitteln lässt.
Satz 8.12 (Lösungen einer Matrix in Zeilenstufenform) Sei eine lineares Gleichungssystem in Zeilenstufenform gegeben mit
(A|b) = 0 BB BB BB BB BB B@
0 . . . 0 a1,j1 ⇤ . . . ⇤ ⇤ . . . ⇤ . . . ⇤ b1
0 . . . 0 a2,j2 ⇤ ⇤ . . . ⇤ b2
0 . . . 0 a3,j3 ⇤ . . . ⇤ b3
... ... ...
ar,jr ⇤ . . . ⇤ br
0 0 . . . 0 br+1
... ... . . .
0 . . . 0 bm
1 CC CC CC CC CC CA ,
(i) Ist nur eins derbr+1, . . . , bm ungleich null, so ist das Gleichungssystem nicht lösbar.
(ii) Sind allebr+1 =. . .=bm = 0, so lässt sich das Gleichungssystem rekursiv auflösen und man benötigt dazu n r freie Parameter.
Beweis. (i) Ist bi 6= 0 mit i r+ 1, so lautet die i-te Gleichung 0·x1 + 0·x2+. . .+ 0·xn=bi 6= 0 und keine Wahl von xkann diese Gleichung lösen.
(ii) Man löst das System von unten nach oben auf. Ausgehend von der r-ten Gleichung ar,jrxjr +ar,jr+1xjr+1+ar,jr+2xjr+2+. . .+ar,nxn =br
wählt man zunächst die Variablen xjr+1, xjr+2, . . . , xn als freie Parameter, die einen be- liebigen Wert annehmen können: xn := 1, . . . , xjr+2 := n jr 1, xjr+1 := n jr. Damit verbleibt nur noch xjr als Variable in der Gleichung und nach dieser kann aufgelöst werden
ar,jrxjr +ar,jr+1 n jr +ar,jr+2 n jr 1+. . .+ar,n 1 =br
)xjr = 1
ar,jr
(br ar,jr+1 n jr ar,jr+2 n jr 1 . . . ar,n 1).
Somit sind nun diexjr, . . . , xnbekannt. Mit derr 1-te Gleichung fährt man analog fort:
Zunächst wählt man für die Variablenxjr 1+1, xjr 1+2, . . . , xjr 1 freie Parameter und löst danach die Gleichung
ar 1,jr 1xjr 1 +ar 1,jr 1+1xjr 1+1+ar 1,jr 1+1xjr 1+1+. . .+ar 1,nxn =br 1
nach xjr 1 auf. Dies ist stets möglich, da die Variablen xjr 1+1, . . . , xn bekannt bzw.
bereits paramterisiert sind. Diese Verfahren führt man bis zur ersten Zeile durch und erhält somit eine Parametrisierung der Lösung.
Die Anzahl der benötigten freien Parameter bestimmt sich dadurch, dass für jede Spalte außer den Spalten mit Pivots ein freier Parameter eingeführt werden muss. Man hat n Unbekannte, r Pivots und dementsprechend n r freie Parameter. ⇤ Man sieht folglich, dass sich Matrizen in Zeilenstufenform direkt lösen lassen. Die Idee des Verfahrens von Gauß ist es nun ein beliebiges Gleichungssystem durch Umformun- gen in ein Gleichungssystem in Zeilenstufenform zu überführen, ohne dass sich dabei die Lösungsmenge ändert. Wesentlich sind dabei die sogenanten elementaren Zeilenumfor- mungen.
Definition 8.13 (elementare Zeilenumformungen)
Eine elementare Zeilenumformung ist eine der folgenden drei Operationen (I) Vertauschung von zwei Zeilen,
(II) Multiplikation einer Zeile mit einer Zahl 6= 0, (III) Addition des -fachen einer Zeile zu einer anderen.
Führt man diese Operationen auf einem Gleichungssystem aus, so bleibt die Lösungs- menge gleich.
Satz 8.14 (Elementare Zeilenumformungen ändern die Lösungsmenge nicht) Ist das Gleichungssystem (Ae|b)e durch endlich viele elementare Zeilenumformungen aus dem Gleichungssystem (A|b) hervorgegangen, dann haben beiden Gleichungssysteme dieselbe Lösungsmenge, d.h.
L(A,b) = L(A,e b).e
Beweis. Es genügt zu zeigen, dass sich die Lösungsmenge bei jeder elementaren Zeile- numformung nicht ändert. Dann ist auch die mehrfache Hintereinanderausführung pro- blemlos möglich.
Die Umformung (I) ändert die Lösungsmenge sicher nicht, denn die Reihenfolge in der die Gleichungen notiert werden ist für die Lösung irrelevant.
Die Umformung (II) ändert die Lösungsmenge nicht, denn durch Multiplikation mit bzw. 1 findet man zunächst die Äquivalenz
ai1x1+. . .+ainxn =bi , ai1x1+. . .+ ainxn= bi.
Erfüllt nun eine Lösung x = (x1, . . . , xn) die linke Gleichung, so auch die rechte und umgekehrt. Daher sind die Lösungsmengen identisch.
Die Umformung (III) ändert die Lösungsmenge ebenfalls nicht, denn die beiden Glei- chungssysteme
ai1x1+. . .+ainxn =bi
ak1x1+. . .+aknxn =bk , ai1x1+. . .+ainxn =bi
(ak1+ ai1)x1+. . .+ (akn+ ain)xn =bk+ bi
sind zueinander äquivalent, wie man durch Addition bzw. Subtraktion sieht. Daher kann man Lösungen des einen Gleichungssystems in Lösungen des zweiten überführen und
umgekehrt. ⇤
Es lässt sich nun aber jedes Gleichungssystem mittels den elementaren Zeilenumformun- gen in ein äquivalentes Gleichungssystem in Zeilenstufenform überführen.
Satz 8.15 (Umformungssatz von Gauß)
Jede Matrix A lässt sich durch elementare Zeilenumformungen in eine Matrix Ae in Zeilenstufenform umformen.
Beweis. Sind alle Einträge der Matrix A 2 Km⇥n gleich Null, so liegt per Definition schon eine Zeilenstufenform mitr= 0 vor und der Satz ist direkt gezeigt. Sei daher min- destens ein Eintrag der Matrix von Null verscheiden und somit gibt es auch mindestens einen Spalte, in der nicht alle Einträge Null sind. Damit kann man sich diejenige solche Spalte mit kleinstem Index suchen, d.h. j1 = min{j|für mindestens ein i gilt aij 6= 0}.
A = 0 BB BB BB
@
0 . . . 0 0 ⇤ . . . ⇤
... ... ... ⇤ . . . ⇤ ... ... ai1,j1 ⇤ . . . ⇤ ... ... ... ⇤ . . . ⇤
0 . . . 0 ⇤ ⇤ . . . ⇤
1 CC CC CC A .
In der j1-ten Spalte ist somit mindestens ein Eintrag ungleich Null. Falls dies nicht bereits der Eintraga1,j1 der ersten Zeile ist, so findet man eine Zeile i1 bei der ai1,j1 6= 0 gilt und durch Vertauschung der i1-ten Zeile mit der ersten Zeile erhält man einen von Null verschiedenen Pivot ea1,j1 = ai1,j1. Durch diese elementare Zeilenumformung vom Typ (I) erhält man somit die erste Zeile der MatrixAe.
Ae = 0 BB BB BB
@
0 . . . 0 ea1,j1 ⇤ . . . ⇤ ... ... ... ⇤ . . . ⇤
... ... ⇤ ⇤ . . . ⇤
... ... ... ⇤ . . . ⇤
0 . . . 0 ⇤ ⇤ . . . ⇤
1 CC CC CC A .
Nun kann man die unterhalb vonea1,j1 stehenden Einträge zu Null machen, indem man die elementare Zeilenumformung vom Typ (III) auf jede der Zeilen anwendet und jeweils ein Vielfaches der ersten Zeile hinzuaddiert. Dabei wählt man für den Eintrag der k-ten Zeile den Faktor so, dass gilt
ak,j1 + ea1,j1 = 0 ) = ak,j1
ea1,j1
. Damit erhält man eine Matrix der Form
Ae1 = 0 BB BB BB
@
0 . . . 0 ea1,j1 ⇤ . . . ⇤ ... ... 0
... ... ... A2
... ... ...
0 . . . 0 0
1 CC CC CC A .
Nun kann man die UntermatrixA2 2Km 1⇥n j1 betrachten und dasselbe Verfahren auf diese anwenden. Damit ergibt sich die zweite Zeile der gesuchten Matrix und man erhält
Ae2 = 0 BB BB BB
@
0 . . . 0 ea1,j1 ⇤ . . . ⇤
... ... 0 0 ea2,j2 . . . ⇤
... ... ... ... 0
... ... ... ... 0 A3
0 . . . 0 . . . 0
1 CC CC CC A .
Nach diesem Muster fährt man fort bis entweder eine Untermatrix vorliegt, die nur Null Einträge besitzt, oder bis keine Untermatrix mehr übrig bleibt, da die Anzahl der
Zeilen/Spalten mit jedem Schritt abnehmen. ⇤
Somit kann nun das gesamte Vorgehen angeben werden.
Definition 8.16 (Eliminationsverfahren von Gauß)
Sei das lineare Gleichungssystem Ax=bmit A2Km⇥n,x2Kn,b2Km gegeben. Das Eliminationsverfahren von Gauß bestimmt die Lösungsmenge L(A,b) durch folgendes Vorgehen:
(a) Notiere die Koeffizientenmatrix (A|b).
(b) Überführe diese durch elementare Zeilenumformungen in (Ae|b)e mit einer Matrix Ae in Zeilenstufenform und bestimme die Anzahl der nicht-Null Zeilen r.
(c) Bestimme anhand der ebr+1, . . . ,ebm, ob einen Lösung exisiert und berechne diese gegebenenfalls als Parametrisierung.
Beispiel 8.17 (i) Das Gleichungssystem
✓ 1 1 5 2 2 12
◆(III) ✓
1 1 5 0 0 2
◆
besitzt keine Lösung, wie man sofort an der letzten Zeile nach der Umformung sehen kann,
L(A,b) =;.
(ii) Das Beispiel vom Anfang des Kapitels liest sich als folgendes Vorgehen 0
@ 2 1 3 8 2 2 4 12 4 4 6 14
1 A(III)
0
@ 2 1 3 8 0 1 1 4 0 6 12 30
1 A(III)
0
@ 2 1 3 8 0 1 1 4 0 0 6 6
1 A(II)
0
@ 2 1 3 8 0 1 1 4 0 0 1 1
1 A und rekursives Auflösen liefert die eindeutige Lösung
L(A,b) ={ 0
@1 3 1
1 A}.
(iii)
0
@ 0 1 4 2 4 2 5 8 8 6 1 2 2 3 1
1 A (I)
0
@ 1 2 2 3 1 2 5 8 8 6 0 1 4 2 4
1 A(III)
0
@ 1 2 2 3 1 0 1 4 2 4 0 1 4 2 4
1 A
(III)
0
@ 1 2 2 3 1 0 1 4 2 4 0 0 0 0 0
1 A(III)
0
@ 1 2 2 3 1 0 1 4 2 4 0 0 0 0 0
1 A
Da für eb3 = 0 gilt, lässt sich dieses Gleichungssystem lösen. Setzt man x3 = 1
und x4 = 2 mit den freien Parametern 1, 2 2R, so erhält man zunächst durch Einsetzen in die zweite Gleichung
0x1+ 1x2+ 4 1+ 2 2 = 4 ) x2 = 4 4 1 2 2. Durch Einsetzen in die erste Gleichung erhält man schließlich
1x1+ 2 (4 4 1 2 2) + 2 1+ 3 2 = 1 ) x1 = 7 + 6 1+ 2. Die Lösungsmenge sieht dementsprechend folgendermaßen aus
L(A,b) = { 0 BB
@
7 + 6 1+ 2
4 4 1 2 2
1 2
1 CC
A2R4| 1, 2 2R}. Dies kann man auch so auffassen, dass die Lösungen durch die Ebene
L(A,b) = { 0 BB
@ 7 4 0 0
1 CC A+ 1
0 BB
@ 6
4 1 0
1 CC A+ 2
0 BB
@ 1
2 0 1
1 CC
A | 1, 2 2R}.
beschrieben werden. Oder anders ausgedrückt: Jede Lösung wird dargestellt mit Hilfe der Vektoren
v0 :=
0 BB
@ 7 4 0 0
1 CC
A,v1 :=
0 BB
@ 6
4 1 0
1 CC
A,v2 :=
0 BB
@ 1
2 0 1
1 CC A
durch eine Linearkombination
x=v0+ 1v1+ 2v2.
Durch direktes Nachrechnen stellt man dabei fest, dass sogar schon alleine v0 eine Lösung ist. Zudem gilt Av1 =0 und Av2 =0.
Bild, Kern und Rang einer Matrix
Dass die Ergebnisse dieser drei Beispiele kein Zufall sind, sondern sehr repräsentative Beispiele von Lösungsarten wiedergeben, zeigt die folgende Betrachtung. Um die Begriff- lichkeiten etwas zu präzisieren, verwendet man die folgenden Definitionen.
Definition 8.18 (Bild und Kern einer Matrix) Für eine MatrixA 2Km⇥n bezeichnet
Im(A) ={Ax | x2Kn}⇢Km das Bild von A, Kern(A) ={x2Kn | Ax=0}⇢Kn den Kern von A.
Der Kern sind also alle Vektoren, die auf den Nullvektor abgebildet werden. Das Bild einer Matrix sind alle möglichen Ergebnisse der Matrixabbildung.
Satz 8.19 (Bild und Kern sind Untervektorräume)
Für eine Matrix A 2 Km⇥n sind das Bild Im(A) ⇢ Km und Kern(A) ⇢ Kn Untervek- torräume.
Beweis. WegenA·0=0ist immer02Kern(A)6=; und02Im(A)6=;. Die anderen Unterraumaxiome sieht man durch elementares Nachrechnen. ⇤ Mit Hilfe von Bild und Kern einer Matrix lässt sich die Lösungsmenge elegant beschrei- ben.
Satz 8.20 (Möglichkeiten der Lösungen eines linearen Gleichungssystems) Sei zub2Kmdie Lösungx2Kndes linearen GleichungssystemAx=bmitA 2Km⇥n gesucht. Dann gilt
(i) Ax=b nicht lösbar , b2/Im(A),
(ii) Ax=b eindeutig lösbar , b2Im(A) und Kern(A) = {0}, (iii) Ax=b mehrdeutig lösbar , b2Im(A) und Kern(A)6={0}, und genau einer dieser drei Fälle trifft zu.
Existiert eine Lösung, so lässt sich diese schreiben als Summe einerspeziellen Lösung des inhomogenen Systems (Ax=b) und jederallgemeinen Lösung des homogenen Systems (Ax=0), d.h. ist x2L(A,b) eine beliebige Lösung, dann gilt
L(A,b) =x+ Kern(A) :={x+x0 | x0 2Kern(A)}.
Beweis. (i) Dies ist die Definition von Im(A).
(ii) + (iii) Da b2Im(A)in beiden Fällen gilt, gibt es mindestens eine Lösung. Es bleibt die Äquivalenz zwischen Eindeutigkeit und Kern(A) ={0} zu zeigen.
“Eindeutigkeit ) Kern(A) = {0}”: Sei x 2 Kn die eindeutige Lösung von Ax = b, und angenommen es existiert y 2 Kern(A),y 6= 0, d.h. Ay = 0. Dann ist wegen A(x+y) =Ax+Ay =Ax=bauchx+yeine Lösung im Widerspruch zur Annahme.
“Kern(A) ={0}) Eindeutigkeit”: Seix2Kn eine Lösung vonAx=b, und angenom- men es existiert noch eine weitere Lösung y 2 Kn,y 6= x mit Ay = b. Dann folgt für z:=y xzum einen z6= 0 und zum anderen
Ay=b ) A(x+z) =b ) Ax+Az=b ) Az=0
und damit z2Kern(A), aber z6=0. Widerspruch zur Annahme. ⇤
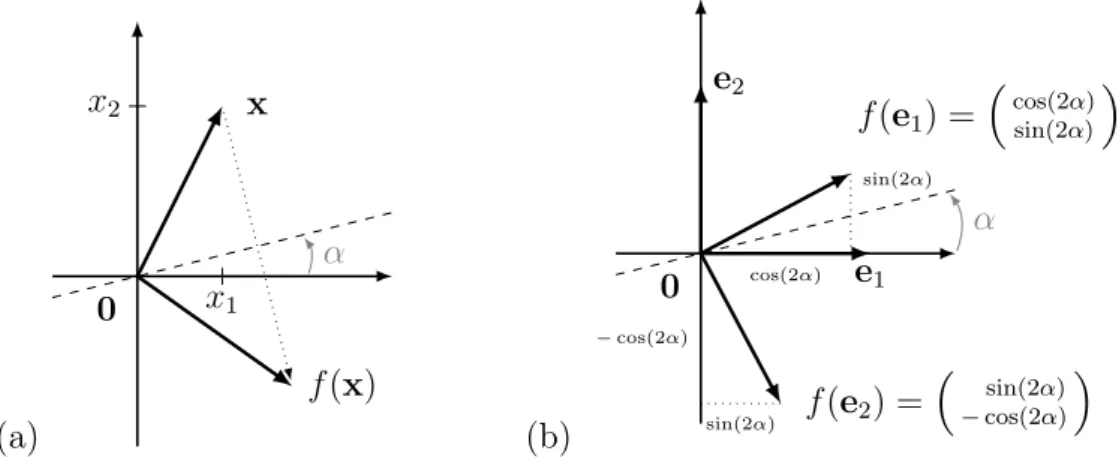
Vom Bild einer Matrix bekommt man eine bessere Vorstellung, wenn man sich das Bild eines Vektors in die Bilder der Einheitsvektoren zerlegt. Für einen beliebigen Vektor xT = (x1, x2, . . . , xn)erhält man die Darstellung
Ax=A(x1e1+x2e2+. . .+xnen)
=x1Ae1+x2Ae2+. . .+xnAen
=x1aS,1 +x2aS,2+. . .+xnaS,n,
wobei diei-te Spalte der MatrixAalsSpaltenvektor aS,iaufgefasst wird. Die Anwendung der Matrix auf einen Einheitsbektor liefert also eine Spalte der Matrix gemäßaS,j =Aej
(1j n). Möchte man daher wissen, wie die Koordinatenachsen abgebildet werden, so muss man sich nur die Spalten der Matrix ansehen. Für einen beliebigen Vektor im Bild gilt zudem, dass er immer eine Linearkombination der Spaltenvektoren ist. Oder anders formuliert: das Bild einer Matrix wird von den Spaltenvektoren aufgespannt.
Definition 8.21 (Zeilen- und Spaltenvektoren) Zu einer Matrix A2Km⇥n nennt man die j-te Spalte
aS,j :=Aej = 0 BB B@
a1j
a2j
...
amj 1 CC
CA, 1j n,
einen Spaltenvektor und diei-te Zeile
aTZ,i := (ai1, ai2, . . . , ain), 1im, einen Zeilenvektor und die Matrix lässt sich somit schreiben als
A = (aS,1aS,2 . . . aS,n) = 0 BB B@
aTZ,1 aTZ,2 ...
aTZ,m 1 CC CA.
Die obige Diskussion hat gezeigt:
Satz 8.22 (Bild einer Matrix wird von den Spaltenvektoren aufgespannt) Das Bild einer Matrix A2Km⇥n wird von den Spaltenvektoren aufgespannt, d.h.
Im(A) = span(aS,1,aS,2, . . . ,aS,n) = span(Ae1,Ae2, . . . ,Aen).
Unter den Spaltenvektoren können natürlich gewisse Vektoren von den anderen linear abhängig sein. Daher ist die Dimension des Bildes maximalnund dies genau dann, wenn alle Spaltenvektoren linear unabhängig sind und somit eine Basis vom Bild bilden.
Definition 8.23 (Rang)
Der Rang einer MatrixA2Km⇥n ist die Dimension des Bildes, d.h.
Rang(A) := dim Im(A).
Der Spaltenrang ist die maximale Anzahl an linear unabhängigen Spalten, d.h.
Spaltenrang(A) := dim span(aS,1,aS,2, . . . ,aS,n).
Der Zeilenrang ist die maximale Anzahl an linear unabhängigen Zeilen, d.h.
Zeilenrang(A) := dim span(aZ,1,aZ,2, . . . ,aZ,m).
Etwas überraschend zeigt sich, dass diese drei Definitionen für jede Matrix diesselbe Zahl beschreiben.
Satz 8.24 (Spaltenrang = Zeilenrang = Rang) Für jede Matrix A 2Km⇥n gilt
Rang(A) = Spaltenrang(A) =Zeilenrang(A).
Beweis. Per Definition ist der Rang die Dimension des von den Spalten von A aufge- spannten Raum. Dieser hat natürlich genau die Dimension, wie es linear unabhängige Spalten gibt.
Um zu zeigen, dass Zeilen- und Spaltenrang identisch sind, muss man mehr Überlegungen anstellen. Zunächst überlegt man sich, dass sich der Zeilen- und Spaltenrang nicht ändert, wenn man in der Matrix eine linear abhängige Zeile entfernt. Dies sieht man wie folgt:
Sei angenommen, dass die i-te Zeile von den anderen linear unabhängig ist, d.h. man kann Koeffizienten µ1, . . . , µm 2K finden, so dass gilt
aZ,i = Xm
k=1k6=i
µkaZ,k
und dies gilt näturlich auch für jede Komponente
aij = Xm
k=1k6=i
µkakj, für alle 1j m.
Entfernt man diese Zeile aus dem Span der Zeilenvektoren, so ändert sich offensichtlich der Zeilenrang nicht. Für den Spaltenrang ist dies nicht so offensichtlich, gilt jedoch auch: Wenn die i-te Zeile aus der Matrix streicht, so sei die so verkleinerte Matrix mit A bezeichnet. Gemäß des Basisauswahlsatzes kann man zunächst aus den Spalten der Matrix A eine Basis des Bildes auswählen. Sei daher (ggf. nach Umnummerierung der Spalten) (a1, . . . ,ar) eine Basis des Bildes. Nun kann man in jedem dieser Vektoren die
i-te Komponente streichen und erhält zunächst ein Erzeugenensystem des Bildes der MatrixAbezeichnet mit(a1, . . . ,ar). Dies stellt aber auch eine Basis dar, denn für eine Linearkombination 1a1+. . .+ rar = 0 folgt für die gestrichenen Komponenten mit
1ai1+. . .+ nair = Xr
j=1
jaij = Xr
j=1 j
Xm
k=1k6=i
µkakj = Xm
k=1k6=i
µk
Xr
j=1
jakj = Xm
k=1k6=i
µk·0 = 0
dass auch die Linearkombination der gestrichenen Zeile Null wäre. Somit kann diese wieder hinzugefügt werden und es ist somit auch 1a1+. . .+ rar= 0 und da dies eine Basis ist, folgt 1 =. . .= r = 0. Damit gilt: Streicht man eine linear abhängige Zeile, so ändert sich der Spaltenrang nicht. Analog kann man folgern: Streicht man eine linear abhängige Spalte, so ändert sich der Zeilenrang nicht.
Nun kann man wie folgt vorgehen: So lange es noch linear abhängige Zeilen oder Spalten gibt, entfernt man diese aus der Matrix, ohne dass sich dabei der Zeilen- und Spaltenrang ändert. Man endet schließlich mit einer MatrixA, die nur noch linear unabhängige Zeilene und Spalten hat. Diese Matrix ist nun aber zwingend quadratisch: gäbe es mehr Spalten als Zeilen, so hätte man Tupel mit so viel Einträgen, wie es Zeilen gibt, davon jedoch so viele wie es Spalten gibt. Aber für ein d-Tupel gibt es maximald linear unabhängige Vektoren. Analog sieht man dass es nicht mehr Zeilen als Spalten geben kann. Somit sieht man: Zeilenrang = Zeilenanzahl = Spaltenanzahl = Spaltenrang. ⇤ Man muss folglich bei einer Matrix nicht zwischen Zeilen- oder Spaltenrang unterschei- den und kann einfach vom Rang sprechen. Der Rang einer Matrix ist dabei eindeutig bestimmt und lässt sich durch das Verfahren von Gauß bestimmen, indem man nach einer Umformung auf Zeilenstufenform die nicht-null Zeilen zählt.
Satz 8.25 (Bestimmung des Rangs einer Matrix) Es gilt:
(i) Die elementaren Zeilenumformungen (I), (II) und (III) ändern den Zeilenrang nicht.
(ii) In einer Matrix in Zeilenstufenform sind die nicht-null Zeilen linear unabhängig.
Beweis. (i) Die Operation (I) vertauscht nur die Zeilen und somit bleibt der Span der Zeilenvektoren gleich. Für die Darstellungsmöglichkeit eines beliebigen Vektorsvändert sich durch Multiplikation der i-ten Zeile mit , d.h. eaZ,i := aZ,i gemäß
v= 1aZ,1+. . .+ iaZ,i+. . .+ maZ,m
,v= 1aZ,1+. . .+ i( aZ,i) +. . .+ maZ,m
auch nichts bei der Operation (II). Analog sieht man, dass die Addition des -fachen der k-ten Zeile zur i-ten, d.h. eaZ,i:=aZ,i+ aZ,k, gemäß
v= 1aZ,1+. . .+ kaZ,k+. . .+ iaZ,i+. . .+ maZ,m
,v= 1aZ,1+..+ ( k i )aZ,k+. . .+ i(aZ,i+ aZ,k) +. . .+ maZ,m
auch der Zeilenrang nicht durch Operation (III) ändert.
(ii) Betrachtet man eine Linearkombination 1aZ,1+ 2aZ,2+. . .+ raZ,r, so kann man sukzessive ausrechnen: Da in Zeilenstufenform nur a1,j1 6= 0 in der ersten Spalte ist, so folgt 1a1,j1 = 0 und daher 1 = 0. Für die zweite Zeile folgt dann mit a2,j2 6= 0 auch
2 = 0. Somit sieht man 1 =. . .= r= 0. ⇤
Damit kann man eine Matrix zunächst in Zeilenstufenform überführen. Die Anzahl der verbleibenden nicht-null Zeilen sind dann genau der Rang der Matrix. Somit lässt sich auch ein praktisches Verfahren angeben, ob ein Vektor b 2 Im(A) enthalten ist oder nicht.
Satz 8.26 (Lösbarkeitskriterium nach Fontené, Rouché und Frobenius) Für ein lineares Gleichungssystem A 2Km⇥n und b2Kn gilt
L(A,b)6=; , Rang(A) = Rang(A,b),
d.h. die Lösungsmenge ist genau dann nicht leer, wenn die um den Vektor b erweiterte Matrix denselben Rang wie die Matrix A besitzt.
Beweis. Ist das System lösbar, so giltb 2Im(A)und somit fügt man durch den Vektor b nur einen von den Spalten der Matrix A linear abhängigen Vektor hinzu. Dies ändert den Spaltenrang nicht und es gilt somit Rang(A) = Rang(A,b).
Umgekehrt gilt sicherlich immer Im(A) ⇢Im(A,b). Gilt nun zudem noch Rang(A) = Rang(A,b), dann muss auch Im(A) = Im(A,b) und damit im Speziellen auch b 2
Im(A) gelten. Damit ist das System lösbar. ⇤
Berechnung einer Basis von Bild und Kern
Durch die Charakterisierung der Lösbarkeit eines Gleichungssystems über das Bild und den Kern einer Matrix ist es sehr interessant diese beiden Räume besser zu kennen.
Speziell lässt sich fragen, wie man eine Basis dieser Untervektorräume berechnen kann und welche Dimension diese besitzen.
Ein praktisches Verfahren, um den Kern einer Matrix zu bestimmen, besteht darin, diese in eine sogenannte reduzierte Zeilenstufenform zu überführen. Diese ist sogar eindeutig bestimmt und aus ihr lässt sich der Kern als auch eine spezielle Lösung (es gibt natürlich beliebig viele spezielle Lösungen, sobald der Kern nicht nur die Null enthält) ablesen.
Definition 8.27 (Reduzierte Zeilenstufenform)
Eine Matrix A2Km⇥n besitzt reduzierte Zeilenstufenform, falls sie in Zeilenstufenform ist und zusätzlich gilt:
(i) Alle Pivots haben den Wert 1, d.h. a1,j1 =. . .=ar,jr = 1.
(ii) Alle weiteren Einträge in den Pivotspalten sind Null, d.h. ai,ji = 0 für i 6=ji und alle Spaltenj1, . . . , jr.
Eine Matrix in reduzierter Zeilenstufenform hat somit die Gestalt
A= 0 BB BB BB BB BB B@
0 . . . 0 1 ⇤ . . . ⇤ 0 ⇤ 0 ⇤ 0 ⇤ . . . ⇤
0 . . . 0 1 ⇤ 0 ⇤ 0 ⇤ . . . ⇤
0 . . . 0 1 ⇤ 0 ⇤ . . . ⇤
... 0 ...
1 ⇤ . . . ⇤
0 0 . . . 0
... ...
0 . . . 0 1 CC CC CC CC CC CA .
Satz 8.28 (Überführung in reduzierte Zeilenstufenform)
Jede Matrix A 2 Km⇥n lässt sich durch elementare Zeilenumformungen in reduzierte Zeilenstufenform überführen.
Beweis. Jede Matrix lässt sich zunächst in Zeilenstufenform überführen. Danach mul- tipliziert man jede Zeile mit dem Inversen des Pivots und erhält somit die Pivots als 1. Nun kann man alle überhalb der Pivots liegenden Einträge durch Addition geeigneter Vielfache der Zeilen zu Null machen, ohne dadurch die Zeilenstufenform zu verlieren. ⇤
Ist eine lineares Gleichungssystem in die reduzierte Zeilenstufenform umgeformt, so las- sen sich nun tatsächlich die Lösungen direkt ablesen.
Satz 8.29 (Lösungen bei reduzierter Zeilenstufenform)
Sei ein lineares Gleichungssystem in reduzierter Zeilenstufenform gegeben mit einem 1rn und den Pivotspalten 1j1 < j2 < . . . < jr n
(A|b) = 0 BB BB BB BB BB B@
0 . . . 0 1 ⇤ . . . ⇤ 0 ⇤ 0 ⇤ 0 ⇤ . . . ⇤ b1
0 . . . 0 1 ⇤ 0 ⇤ 0 ⇤ . . . ⇤ b2
0 . . . 0 1 ⇤ 0 ⇤ . . . ⇤ b3
... 0 ... ...
1 ⇤ . . . ⇤ br
0 0 . . . 0 br+1
... ... ...
0 . . . 0 bm
1 CC CC CC CC CC CA .
Dann gilt:
(i) Ist nur eines der br+1, . . . , bm ungleich Null, so hat das System keine Lösung.
(ii) Der Vektor xmit
xk:=
8>
<
>:
bi, wenn k=ji
eine Pivotspalte ist, 0, sonst,
also 0 BB BB BB BB BB BB BB B@
1 CC CC CC CC CC CC CC CA 0...
0
b1 j1-te Zeile 0...
0
b2 j2-te Zeile 0...
ist eine spezielle Lösung des Gleichungssystems Ax=b.
(iii) Für jede der Nichtpivotspalten j = 1, . . . , n, j /2 {j1, . . . , jr} ist der aus den Ein- trägen der Spalte gebildete Vektor xj mit
(xj)k :=
8>
>>
<
>>
>:
aij, wennk =ji
eine Pivotspalte ist, 1, wennk =j,
0, sonst,
also
0 BB BB BB BB BB BB BB BB BB BB BB BB BB
@ 1 CC CC CC CC CC CC CC CC CC CC CC CC CC A 0...
0
a1j j1-te Zeile 0...
0
a2j j2-te Zeile 0...
0
1 j-te Zeile
0...
0
eine Lösung des GleichungssystemsAx=0. Zudem sind die so definierten Vektoren xj, j = 1, . . . , n, j /2{j1, . . . , jr} eine Basis von Kern(A).
Beweis. (i) Gilt bereits schon für Zeilenstufenform.
(ii) Dass xeine Lösung des Systems ist, sieht man durch direktes Nachrechnen. Betrach- tet man nämlich das Ergebnis der Multiplikation dieses Vektors mit der i-ten Zeile, so
ergibt sich X
k=1,...,n
aikxk = X
k=1,...,n k2{j1,...,jr}
aikxk+ X
k=1,...,n k /2{j1,...,jr}
aikxk = X
s=1,...,r
ai,js·bs+ X
k=1,...,n k /2{j1,...,jr}
aik·0 =bi,
da in deri-ten Zeile nur für die Pivotspalteji der Eintragai,ji 6= 0ist und an den anderen Pivotspalten eine Null steht.
(iii) Dass die so definierten xj eine Lösung von Ax = 0 ist, sieht man ebenfalls durch direktes Nachrechnen. Betrachtet man nämlich das Ergebnis der Multiplikation dieses Vektors mit deri-ten Zeile, so ergibt sich
X
k=1,...,n
aik·(xj)k = X
k=1,...,n k2{j1,...,jr}
aik·(xj)k+aij ·(xj)j + X
k=1,...,n k /2{j,j1,...,jr}
aik·(xj)k
= X
s=1,...,r
ai,js ·asj +aij ·( 1) + X
k=1,...,n k /2{j,j1,...,jr}
aik·0
=aij aij = 0.
Um zu zeigen, dass die so definiertenxj linear unabhängig sind, sei X
k=1,...,n k /2{j1,...,jr}
kxk =0
eine Linearkombination des Nullvektors. Seil n der höchste Index in der Summe mit l /2 {j1, . . . , jr}. Dann gilt für den l-ten Eintrag (xk)l = 1 für k =l, jedoch (xk)j = 0 für j < l. Damit folgt l = 0. Analog fährt man mit dem nächst größten Index in der Summe fort und schließt analog. Nach und nach sind somit alle k = 0.
Um zu zeigen, dass es sich um ein Erzeugendensystem handelt, sei v 2 Kern(A) ein beliebiger Vektor aus dem Kern, d.h. es gilt
X
k=1,...,n
aikvk= 0, für alle i= 1, . . . , m.
Nun gilt für alle i= 1, . . . , munter Verwendung von ij := (1n)ij
0 = X
k=1,...,n
aik·vk= X
k=1,...,n
(aik ik)·vk+ X
k=1,...,n
ik·vk= X
k=1,...,n
(aik ik)·vk+vi
und somit
vi = X
k=1,...,n k /2{j1,...,jr}
( vk)·(aik ik) + X
k=1,...,n k2{j1,...,jr}
( vk)·(aik ik)
= X
k=1,...,n k /2{j1,...,jr}
( vk)(xk)i+ X
k=1,...,n k2{j1,...,jr}
( vk)·0
und jeder Vektor aus dem Kern lässt sich kombinieren. ⇤
Beispiel 8.30 Die Matrix
0
@ 1 2 2 3 1 0 0 2 2 4 0 0 0 0 0
1 A(II)
0
@ 1 2 2 3 1 0 0 1 1 2 0 0 0 0 0
1 A(III)
0
@ 1 2 0 1 3 0 0 1 1 2 0 0 0 0 0
1 A
kann auf reduzierte Zeilenstufenform gebracht werden. Die Lösungen der Gleichung liest man am Einfachsten durch eine Hilfskonstruktion ab: Zunächst fügt man an den Stufen- stellen so viele Nullzeilen ein, bis alle Pivots auf der Diagonalen stehen. Danach werden nach dem letzten Pivot Nullzeilen hinzugefügt oder entfernt, bis eine quadratische Ma- trix verbleibt. Schließlich ersetzt man gedanklich noch alle Nullen auf der Diagonale durch eine 1in den Nullzeilen. Man findet somit als Hilfsdarstellung
0
@ 1 2 0 1 3 0 0 1 1 2 0 0 0 0 0
1 A
0 BB
@
1 2 0 1 3 0 0 0 0 0 0 0 1 1 2 0 0 0 0 0
1 CC A
0 BB
@
1 2 0 1 3 0 1 0 0 0 0 0 1 1 2 0 0 0 1 0
1 CC A,
und liest die Lösung wie folgt ab: In den Nichtpivotspalten (hier: Spalte 2 und 4) stehen die gesuchten homogenen Lösungen, die eine Basis vom Kern bilden, und in der letzten Spalte (hier: Spalte 5) steht eine spezielle Lösung. Somit lässt sich jede Lösung schreiben als
x= 0 BB
@ 3 0 2 0
1 CC A+ 1
0 BB
@ 2
1 0 0
1 CC A+ 2
0 BB
@ 1 0 1 1
1 CC A.
Vom Bild ist bereits bekannt, dass es per Definition als Dimension den Rang der Matrix haben muss und dieser Rang konnte mittels Gauß-Verfahren und elementaren Zeilenum- formungen gewonnen werden, bei denen sich der Rang nicht änderte. Jedoch ändert sich natürlich das Bild der Matrix (wenn auch nicht dessen Dimension), sobald man elementare Zeilenumformungen durchführt und daher kann eine Basis vom Bild nicht nach Umformungen auf Zeilenstufenformen abgelesen werden. Das Bild der Matrix wird jedoch von den Spalten aufgespannt und daher kann man grundsätzlich aus den Spalten der Matrix eine Basis auswählen. Dies ist in der Praxis jedoch unhandlich. Viel besser ist es, wenn man sich aus diesen Vektoren eine Basis linear kombiniert. Dazu kann man Spalten tauschen, Spalten mit Skalaren multiplizieren oder das Vielfache einer Spalten zu einer anderen hinzufügen - oder anders gesagt: man führt das Gauß-Verfahren auf den Spalten durch. Dies kann man direkt so auffassen, dass man das Verfahren mit Zei- lenumformungen auf der transponierten Matrix durchführt und man erhält somit die analogen Definitionen Spaltenstufenform und elementare Spaltenumformungen.
✓ 1 1 2 1 0 0
◆ ✓
1 0 0 1 1 2
◆ ✓
1 0 0 1 1 0
◆ ✓
1 0 0 0 1 0
◆
An den letzen beiden Darstellungen liest man ab: Eine Basis des Bildes ist gegeben durch (
✓1 1
◆ ,
✓0 1
◆
) oder auch (
✓1 0
◆ ,
✓0 1
◆ ).
Aus der reduzierten Zeilenstufenform konnte eine Basis des Kerns direkt als die Anzahl der Nichtpivotspalten bestimmt werden. Hat eine Matrix die Größem⇥nund den Rang r, dann sind dies genaun Spalten minus dierPivotspalten und damit ist die Dimension des Kerns k :=n r.
Satz 8.31 (Dimensionsformel für Rang und Kern von Matrizen) Sei A2Km⇥n und r:= Rang(A) sowiek := dim Kern(A). Dann gilt
n=k+r,
d.h. die Dimension des Bildes plus die Dimension des Kerns ergibt die Dimension des Urbildraums.
Diesen Zusammenhang wird sich später ganz allgemein wiederfinden. Für die Lösbarkeit von Matrizengleichungen liefert die Dimensionsformel eine sehr griffige Formulierung der Lösbarkeit.
Satz 8.32 (Lösungen von Gleichungssystemen)
Seien die n Komponenten der Lösung x 2 Kn des linearen Gleichungssystem Ax = b mit A 2 Km⇥n und b 2 Km gesucht und der Rang der Matrix durch r := Rang(A) gegeben. Dann gilt für die Größe des Lösungsraums:
(i) Kern(A) = L(A,0)⇢Kn ist ein Untervektorraum der Dimension n r.
(ii) Existiert eine Lösung, dann ist der Lösungsraum L(A,b) ⇢Rn ein affiner Unter- raum der Dimension n r und mit jeder speziellen Lösung x2L(A,b)gilt
L(A,b) =x+L(A,0).
Als Kriterien für die Lösbarkeit findet man:
(iii) Zub 2Rm ist Ax=b lösbar , Rang(A) = Rang(A,b), (iv) Zub 2Rm ist Ax=b eindeutig lösbar , Rang(A) = Rang(A,b) =n, (v) Für jedes b 2Rm ist Ax=b lösbar , Rang(A) =m.
Beweis. (i) Die Größe von dim Kern(A) folgt direkt aus der Dimensionsformel mit r = dim Im(A). (ii)+(iii) sind bereits bewiesene Aussagen. (iv) erweitert (iii) um die Eindeutigkeit. Dies folgt, da mit dim Im(A) = n auchdim Kern(A) = 0 gilt und somit Kern(A) = {0}. (v) Rang(A) = m bedeutet, dass die Abbildung surjektiv ist. Damit gibt es mindestens eine Lösung.
Für den wichtigen Spezialfall m = n, d.h. Abbildungen des Rn auf sich selbst, erhält man zudem folgendes.
Satz 8.33 (Lösbarkeit bei quadratischen Matrizen)
Für eine quadratische Matrix A 2Kn⇥n und einen beliebigen Vektor b2Kn gilt:
Ax=b ist eindeutig lösbar , Rang(A) =n.
Beweis. Da Rang(A) = n gilt, ist die Abbildung surjektiv und damit sogar bijektiv.
Durch die inverse Abbildung A 1 erhält man stets die eindeutige Lösung x=A 1b. ⇤
8.3 Elementarmatrizen und inverse Matrizen
Der Ablauf das Gauß-Verfahrens lässt sich formal auch als eine Multiplikation durch geeignete Matrizen beschreiben, d.h. wird eine Matrix A ! Ae durch einen elementare Zeilenumformung überführt, dann lässt sich dies auch schreiben als Ae =E·Amit einer geeigneten Matrix E, die diese Transformation bewirkt. Die dazu geeigneten Matrizen werden entsprechend als Elementarmatrizen bezeichnet.
Definition 8.34 (Elementarmatrizen)
Sei m 2 N und zwei Zeilenindizes i, j mit 1 i, j m beliebig gewählt. Als Element- armatrizen bezeichnet man eine der folgenden drei quadratischen Matrizen aus Km⇥m, die durch Anwendung von elementaren Zeilenumformungen aus 1m hervorgehen:
(I) EIij durch Vertauchung der i-ten Zeile mit derj-ten Zeile von 1m
EIij :=
0 BB BB BB BB BB BB BB BB B@
1 CC CC CC CC CC CC CC CC CA 1 ...
1
. . . 0 . . . 1 . . . i-te Zeile
1 ...
1
. . . 1 . . . 0 . . . j-te Zeile
1 ...
1
(II) EIIi ( ) durch Multiplikation deri-ten Zeile von 1m mit einer Zahl 6= 0
EIIi ( ) = 0 BB BB BB BB BB BB BB BB B@
1 CC CC CC CC CC CC CC CC CA 1 ...
1
. . . i-te Zeile
1 ...
1 1
1 ...
1
(III) EIIIij ( ) durch Addition des -fachen derj-ten Zeile zur i-ten Zeile von 1m
EIIIij ( ) = 0 BB BB BB BB BB BB BB BB B@
1 CC CC CC CC CC CC CC CC CA 1 ...
1
. . . 1 . . . i-te Zeile
1 ...
1
. . . 1 . . . j-te Zeile
1 ...
1
In analoger Weise lassen sich dies Matrizen auch als elementare Spaltenoperationen auffassen. Diese Elementarmatrizen sind nun sehr hilfreich zur Darstellung von Matri- xumformungen.
Satz 8.35 (Elementarmatrizen bewirken elementare Zeilen- und Spaltenope- rationen)
Aus der seien MatrixAseien die folgenden Matrizen durch elementare Zeilenoperationen hervorgegangen:
(I) AI durch Vertauchung der i-ten Zeile mit derj-ten Zeile, (II) AII durch Multiplikation deri-ten Zeile mit einer Zahl 6= 0, (III) AIII durch Addition des -fachen derj-ten Zeile zur i-ten Zeile,
dann lässt sich dies Darstellen als Multiplikation von links mit einer Elementarmatrix (I) AI=EIij ·A, (II) AII=EIIi ( )·A, (III)AIII =EIIIij ( )·A.
Analog seien die folgenden Matrizen durch elementare Spaltenoperationen aus A her- vorgegangen:
(I) AI durch Vertauchung deri-ten Spalte mit der j-ten Spalte, (II) AII durch Multiplikation der i-ten Spalte mit einer Zahl 6= 0, (III) AIII durch Addition des -fachen der i-ten Spalte zur j-ten Spalte,
dann lässt sich dies Darstellen als Multiplikation von rechts mit einer Elementarmatrix (I) AI=A·EIij, (II) AII=A·EIIi ( ), (III)AIII =A·EIIIij ( ).
Bei der Multiplikation mit einer Elementarmatrix ändert sich der Rang der Matrix nicht.
Beweis. Elementares Nachrechnen. ⇤
Damit lässt sich das Verfahren von Gauß dadurch kennzeichnen, dass man eine Multi- plikation mit Elementarmatrizen durchführt.
Satz 8.36 (Gauß-Elimination durch Elementarmatrizen)
Zu jeder Matrix A2 Km⇥n gibt es Elementarmatrizen E1, . . . ,Es 2Km⇥m, so dass die Matrix
Ae =Es·. . .·E2·E1 ·A eine Zeilenstufenform besitzt.
Analog gibt es Elementarmatrizen E01, . . . ,E0t2Km⇥m, so dass die Matrix Ae =A·E01·E02·. . .·E0t
eine Spaltenstufenform besitzt.
Beweis. Dies ist die äquivalente Formulierung des bereits bewiesenen mit Elementar- matrizen.
Damit lässt sich auch noch ein anderer Blick auf den Rang der Matrix werfen. Es gilt nämlich der folgende Satz.
Satz 8.37 (Transformation auf Diagonalgestalt)
Zu jeder Matrix A 2 Km⇥n mit r := Rang(A) gibt es zwei Matrizen E 2 Km⇥m und E0 2Kn⇥n, so dass man die Matrix auf die folgende Gestalt umformen kann:
E·A·E0 =
✓1r 0 0 0
◆ und diese Matrizen sind Produkte von Elementarmatrizen
E=Es·. . .·E2·E1, E0 =E01·E02·. . .·E0t.
Beweis. Nach dem Verfahren von Gauß lässt sich durch Multiplikation mit Element- armatrizen von links - d.h. durch elementare Zeilenumformungen - die Matrix zunächst auf reduzierte Zeilenstufenform bringen:
Ae = 0 BB BB BB BB BB B@
0 . . . 0 1 ⇤ . . . ⇤ 0 ⇤ 0 ⇤ 0 ⇤ . . . ⇤
0 . . . 0 1 . . . 0 ⇤ 0 ⇤ . . . ⇤
0 0 0 1 ⇤ 0 ⇤ . . . ⇤
... ...
1 ⇤ . . . ⇤
0 0
1 CC CC CC CC CC CA .
Die bis hierher durchgeführten Zeilenumformungen bilden die Matrix E = Es ·. . . · E1. Nun beginnt man mit den Spaltenumformungen und bringt durch Vertauschen der Spalten die Pivots nach links auf die Diagonale:
Ae = 0 BB BB BB BB BB B@
1 0 . . . 0 ⇤ . . . ⇤ . . . ⇤
1 0 . . . 0 ⇤ . . . ⇤ . . . ⇤
1 0 0 ⇤ . . . ⇤ . . . ⇤
... ... . . . ... ...
1 ⇤ . . . ⇤ . . . ⇤
0 0
1 CC CC CC CC CC CA .
Nun kann man durch Addition eines Vielfachen der Pivot-Spalten zu den rechts stehen- den Spalten den Rest der Matrix zu Null machen:
Ae = 0 BB BB BB BB BB B@
1 0 . . . 0 . . . 0 . . . 0
1 0 . . . 0 . . . 0 . . . 0
1 0 . . . 0 . . . 0 . . . 0
... ... . . . ... ...
1 0 . . . 0 . . . 0
0 0
1 CC CC CC CC CC CA .
Die durchgeführten Spaltenumformungen bilden die MatrixE0 =E01·. . .·E0t.
Dieses Vorgehen zeigt wieder, dass Spaltenrang gleich Zeilenrang ist, denn: Der Zeilen- und Spaltenrang ändert sich nicht bei den elementare Zeilen- und Spaltenumformungen.
Daher haben die ursprüngliche MatrixAund die transformierteAe =E·A·E0 denselben Zeilen- und Spaltenrang. Es bildet sich jedoch stets eine quadratische Teilmatrix, an der man den Rang direkt ablesen kann.
Möchte man die Matrizen E und E0 explizit berechnen, so bietet sich das folgenden Vorgehen an: Man schreibt sich drei Matrizen 1m, A, 1n nebeneinander. Nun formt man zunächst die Matrix A durch Zeilenumformungen in reduzierte Zeilenstufenform um und nimmt dabei dieselben Umformungen an der Matrix 1m vor. Dann formt man die Matrix Adurch Spaltenumformungen weiter in die gesuchte Gestalt um und nimmt dabei gleichzeitig dieselben Spaltenumformungen an der Matrix 1n vor. Man hat also das Schema
1m A 1n
E1·1m E1·A ...
... ... ...
Es·. . .·E1·1m Es·. . .·E1·A 1n
... Es·. . .·E1·A·E01 1n·E01
... ... ...
Es·. . .·E1·1m Es·. . .·E1·A·E01·. . .·E0t 1n·E01·. . .·E0t und kann somit die Matrizen E und E0 direkt ablesen.
Beispiel 8.38
Durch die simultanen Umformungen
12 A 13
✓ 1 0 0 1
◆ ✓ 1 3 1
2 8 6
◆ ...
EIII21( 2) · x ✓
1 0 2 1
◆ ✓ 1 3 1
0 2 4
◆ EII2(12) · x ✓
1 0 1 12
◆ ✓ 1 3 1
0 1 2
◆ EIII12( 3) · x ✓
4 32 1 12
◆ ✓ 1 0 5
0 1 2
◆ 0
@ 1 0 0
0 1 0
0 0 1
1 A
y · EIII13(5)
✓ 1 0 0
0 1 2
◆ 0
@ 1 0 5
0 1 0
0 0 1
1 A
y · EIII23( 2)
... ✓
1 0 0
0 1 0
◆ 0
@ 1 0 5
0 1 2
0 0 1
1 A
=:E =:E0
findet man
E=EIII12( 3)·EII2(12)·EIII21( 2)·12, E0 =13·EIII13(5)·EIII23( 2)