Semiklassische Betrachtung von zwei Bosonen auf einer Linie mit Kontaktwechselwirkung

Semiklassische Betrachtung von zwei Bosonen auf einer Linie mit Kontaktwechselwirkung

Zulassungsarbeit

von

Benjamin Geiger aus

Regensburg

vorgelegt am: 22. Juli 2014

durchgef¨ uhrt am

Institut I f¨ ur theoretische Physik der Universit¨ at Regensburg

unter Anleitung von

Prof. Dr. Klaus Richter

Inhaltsverzeichnis

Inhaltsverzeichnis

1. Einleitung 5

2. Vorbereitende Konzepte 7

2.1. Notation und Konventionen . . . . 7

2.2. Propagator und Zustandsdichte . . . . 7

2.3. Semiklassische Zustandsdichte . . . . 9

2.4. Freier Propagator und Randkorrekturen . . . 10

2.5. Vielteilchen-Propagator . . . 12

2.6. Lokale Zustandsdichte f¨ ur eindimensionale Systeme . . . 14

3. Herleitung des Propagators f¨ ur ein Deltapotential 17 3.1. Exakte L¨ osungen f¨ ur den Potentialtopf mit Delta-Barriere . . . 17

3.2. Propagator f¨ ur eine Delta-Barriere . . . 19

4. Zustandsdichte in einer Dimension mit Kontaktwechselwirkung 25 4.1. Herleitung der Zustandsdichte . . . 25

4.2. Grenzf¨ alle . . . 27

4.3. Vergleich mit der quantenmechanischen Zustandsdichte . . . 28

5. Zustandsdichte f¨ ur zwei Bosonen auf einer Linie mit Kontaktwechselwirkung 31 5.1. Zustandsdichte mit Randkorrekturen . . . 31

5.2. Korrekturen von den Ecken . . . 33

5.3. Zusammenfassung und Analyse . . . 42

5.4. Vergleich mit den quantenmechanischen L¨ osungen . . . 44

6. Lokale Zustandsdichte f¨ ur zwei Bosonen auf einer Linie 51 6.1. Quantenmechanische lokale Zustandsdichte . . . 51

6.2. Semiklassische lokale Zustandsdichte . . . 53

6.3. Verhalten in der N¨ahe des Randes . . . 65

6.4. Vergleich der Ergebnisse . . . 67

7. Ausblick 71 A. Anhang 73 A.1. Umformung des Produkts aus Wellenfunktionen . . . 73

A.2. Numerische Berechnung der Wellenzahlen . . . 74

A.3. Bestimmung der Differentialgleichungen bei der lokalen Zustandsdichte . . 74

A.4. Laplace-Transformation . . . 77

1. Einleitung

Anfang des vergangenen Jahrhunderts f¨ uhrten neue experimentelle Ergebnisse wie z.B.

die diskreten Absorptions- bzw. Emissionsspektren bei Atomen und der bei elektroma- gnetischen Wellen festgestellte Teilchencharakter zu Unstimmigkeiten mit den bis dahin etablierten Theorien. Die aus der darauffolgenden Suche nach neuen Theorien hervorge- gangene Quantenmechanik und die auf ihr aufbauenden Theorien bilden bis heute die am besten best¨ atigten physikalischen Theorien und sind dementsprechend der Hauptbe- standteil der modernen Physik. Allerdings sind diese Theorien um ein vielfaches kom- plizierter als die klassischen Theorien und k¨onnen selbst f¨ ur vergleichsweise einfache physikalische Systeme oft nur mit Hilfe numerischer Methoden ¨ uberpr¨ ufbare Vorher- sagen treffen. Da die Quantenmechanik in makroskopischen Dimensionen die gleichen Vorhersagen macht wie die newtonsche Theorie, m¨ ussen sich klassische Trajektorien in irgendeiner Weise auch in den quantenmechanischen Ergebnissen wiederspiegeln. Die semiklassische Physik ist im ¨ Ubergang zwischen klassischer Mechanik und Quantenme- chanik angesiedelt und liefert einerseits analytische N¨aherungen f¨ ur die exakten quanten- mechanischen L¨ osungen und andererseits Interpretationsm¨ oglichkeiten der gefundenen L¨ osungen in diesem Kontext. Vor allem bei Systemen, die sich klassisch chaotisch ver- halten und quantenmechanisch nicht exakt l¨ osbar sind, liefert der semiklassische Ansatz gute Ergebnisse. Gutzwiller [3] stellte 1971 mit seiner Spurformel eine M¨oglichkeit vor, die quantenmechanische Zustandsdichte eines solchen Systems allein mit Hilfe der Ei- genschaften der klassisch erlaubten periodischen Trajektorien zu approximieren. Balian und Bloch [5] leiteten mit semiklassischen Methoden kurz sp¨ ater eine sehr einfache Ent- wicklung des nicht oszillierenden Teils der Zustandsdichte in Potenzen der Energie her und verallgemeinerten damit die schon viel fr¨ uher von Weyl [15] aufgestellte (und nach ihm benannte) Entwicklung.

Eine der gr¨ oßten Herausforderungen in der aktuellen Forschung bildet die Einbezie-

hung der Wechselwirkung in Systemen aus mehreren Teilchen. F¨ ur relativistische Streu-

prozesse liefert die Quantenelektrodynamik gute Ergebnisse, w¨ ahrend im nichtrelativis-

tischen Fall die Bornsche N¨aherung verwendet werden kann (in beiden F¨allen handelt es

sich um St¨ orungstheorien). F¨ ur nichtrelativistische wechselwirkende Teilchen in einem

begrenzten Gebiet k¨onnen diese jedoch in der Regel zu keinem Zeitpunkt als unabh¨angig

betrachtet werden. F¨ ur einzelne Atome wurde sehr fr¨ uh von Thomas und Fermi eine

N¨aherungsl¨ osung vorgeschlagen, die f¨ ur hohe Kernladungszahlen qualitativ gute Ergeb-

nisse liefert. Sp¨ ater konnten mit Hilfe der Hartree-Fock N¨aherung die wichtigsten Ei-

genschaften von Atomen sehr gut beschrieben werden. F¨ ur fermionische oder bosonische

Gase gibt es ebenfalls zahlreiche Ans¨ atze, jedoch verkompliziert die Einbeziehung der

Wechselwirkung in jedem Fall die Rechnungen. Ist man lediglich an der mittleren Zu-

standsdichte eines solchen Gases interessiert, k¨onnte die semiklassische Physik wie im

nichtwechselwirkenden Fall m¨ oglicherweise einfache, universelle und analytisch erfassbare

Ergebnisse liefern. Q. Hummel [6] stellte dazu 2014 einen Formalismus zur semiklassi-

schen Berechnung der Zustandsdichte f¨ ur beliebig viele Fermionen bzw. Bosonen vor, die

sich in einem begrenzten Volumen beliebiger Dimension befinden und nicht miteinander

wechselwirken. Der Formalismus ber¨ ucksichtigt dabei bereits die quantenmechanische

Ununterscheidbarkeit der Teilchen.

Um diesen Formalismus auf wechselwirkende Systeme zu erweitern, ist es sinnvoll, zuerst den einfachsten Fall eines Systems aus zwei Teilchen in einem eindimensionalen Volumen (d.h. auf einer begrenzten Linie) zu betrachten. Diese Arbeit besch¨ aftigt sich deshalb mit einem System aus zwei Bosonen auf einer Strecke der L¨ ange L, die einer Kontaktwechselwirkung in Form eines Delta-Potentials V (q ₁ , q ₂ ) = αδ(q ₁ − q ₂ ) unterlie- gen. Dieses kann als Grenzfall eines sehr kurzreichweitigen Potentials aufgefasst werden, was f¨ ur hohe Teilchenenergien es eine physikalisch sinnvolle N¨aherung darstellt. Neben der Vereinfachung der Rechnungen hat dieses Potential den folgenden Vorteil: ein Sys- tem aus beliebig vielen Bosonen auf einer Linie mit einer δ-artigen Wechselwirkung kann quantenmechanisch exakt gel¨ ost werden [7] und l¨ asst deshalb einen einfachen Vergleich der semiklassischen N¨aherungen mit dem quantenmechanischen Ergebnis zu.

Im ersten Abschnitt der Arbeit werden die grundlegenden mathematischen und phy- sikalischen Konzepte vorgestellt, die zur Berechnung der Zustandsdichte f¨ ur das System aus zwei Bosonen ben¨ otigt werden. Der darauffolgende Abschnitt besch¨ aftigt sich mit der Herleitung des eindimensionalen Propagators f¨ ur ein Delta-Potential und verallgemeinert das bereits von Manoukian gefundene Ergebnis [8]. Um die grundlegenden Eigenschaften dieses Ergebnisses zu ergr¨ unden schließt sich eine kurze Betrachtung eines Einteilchen- problems unter der Verwendung des hergeleiteten Propagators an. Dabei wird auch die Formulierung der Wechselwirkung als gemischte Randbedingung hervorgehoben, was die Rechnungen in den darauf folgenden Abschnitten vereinfacht.

Der n¨ achste Abschnitt befasst sich in aller Ausf¨ uhrlichkeit mit der Zustandsdichte f¨ ur das System aus zwei wechselwirkenden Bosonen. Dabei wird zuerst die Weyl-Entwicklung bis zur Ordnung E ⁻

berechnet. Die Rechnungen und das Ergebnis sind dabei sehr

¨

uberschaubar und lassen hoffen, dass f¨ ur h¨ ohere Teilchenzahlen keine weiteren Korrek- turen verwendet werden m¨ ussen. Diese Korrekturen werden im Anschluss berechnet und analysiert. Im Vergleich mit den exakten quantenmechanischen L¨ osungen wird dann er- sichtlich, dass die h¨ oheren Korrekturen im Allgemeinen vernachl¨ assigbar sind bzw. durch einfachere Ausdr¨ ucke ersetzt werden k¨onnen.

Im letzten Abschnitt wird die lokale Zustandsdichte und die Teilchendichte f¨ ur das System berechnet und mit den quantenmechanischen Ergebnissen verglichen. Dieser Ab- schnitt gestaltet sich sehr technisch und zeigt, dass auch f¨ ur das vergleichsweise einfache System aus zwei wechselwirkenden Bosonen die lokalen Eigenschaften semiklassisch be- schrieben werden k¨onnen, der dazu ben¨ otigte Aufwand im Vergleich jedoch sehr hoch ist.

In einem Unterabschnitt wird das Verhalten in unmittelbarer N¨ahe des Randes aus der

Potenzreihenentwicklung der lokalen Zustandsdichte gewonnen. Dieses liefert ein sehr

einfaches Ergebnis, das die Wechselwirkung in einfacher Form widerspiegelt.

2. Vorbereitende Konzepte

2.1. Notation und Konventionen

• Vektoren werden in dieser Arbeit im Vergleich zu skalaren Gr¨ oßen als aufrecht stehende, fett gedruckte Buchstaben gekennzeichnet. Beispiel: x, t, β sind Skalare, x ist ein Vektor.

• Die auftretenden Funktionen h¨ angen oft von mehreren Variablen ab. Falls die Abh¨ angigkeit von einer bestimmten Variable in einem gegebenen Zusammenhang nicht relevant ist, so wird diese oft weggelassen, um die Notation zu vereinfachen.

• Treten in einer Formel die Koordinaten q ₁ und q ₂ auf, so sind damit immer die physikalischen Koordinaten gemeint (die Umkehrung gilt nicht).

2.2. Propagator und Zustandsdichte

Der Propagator eines quantenmechanischen Systems ist definiert als [3]

K(x ^′ , x, t) := h x ^′ | U ˆ (t) | x i , (1) mit dem Zeitenwicklungs-Operator ˆ U (t) = e ⁻

^{H ˆ t} . Der Propagator entspricht einer Wahr- scheinlichkeitsdichte daf¨ ur, ein Teilchen, das sich zum Zeitpunkt 0 am Ort x befand, nach der Zeit t am Ort x ^′ zu finden. Per Definition erf¨ ullt der Propagator f¨ ur t 6 = 0 die zeitabh¨ angige Schr¨ odinger-Gleichung

i ~ ∂

∂t K (x ^′ , x, t) = ˆ H ^x K(x ^′ , x, t) (2) und f¨ ur t = 0 gilt K(x ^′ , x, 0) = δ(x ^′ − x).

Sind die station¨ aren L¨ osungen des Systems bekannt, so gilt ¹ U ˆ (t) = e ⁻

^{H ˆ t} = ^X

n

e ⁻

^E

^t | ψ n i h ψ n | . (3) Sei Ω der Konfigurationsraum des Systems und x, x ^′ ∈ Ω. Der Propagator kann dann mit h x | ψ n i = ψ n (x) als

K(x ^′ , x, t) = ^X

n

e ⁻

^E

^t ψ _n ^∗ (x ^′ )ψ n (x) (4) geschrieben werden. Die Spur des Propagators f¨ ur ein System mit Konfigurationsraum Ω wird definiert als

Tr K(x ^′ , x, t) :=

Z

Ω dx K(x, x, t), und entspricht der Spur des Zeitentwicklungs-Operators.

1

F¨ ur ein kontinuierliches Spektrum muss die Summe durch ein Integral ersetzt werden.

Die exakte Zustandsdichte f¨ ur ein System mit diskreten Eigenenergien E n ist gegeben durch ρ(E) = ^P _n δ(E − E n ) und gibt ¨ uber das Integral

Z E

+∆E E

dE ρ(E) (5)

die Anzahl der Zust¨ande mit einer Energie im Intervall [E ₀ , E ₀ +∆E] an. Die Z¨ ahlfunktion wird deshalb definiert als

N (E) :=

Z E

−∞ dE ^′ ρ(E ^′ ). (6)

Sie gibt die Anzahl der Zust¨ande mit einer Energie E ^′ < E an. Die Z¨ ahlfunktion ist im Vergleich zur Zustandsdichte eine Funktion im klassischen Sinne und wird deshalb f¨ ur den Vergleich von quantenmechanischer und semiklassischer Zustandsdichte verwendet.

Die Z¨ ahlfunktion f¨ ur ein System mit diskretem Spektrum ist eine st¨ uckweise konstante Funktion

N (E) = ^X

n

Θ(E − E n ) (7)

mit der Heaviside-Theta-Funktion Θ(E).

Mit dem Parameter β = _~ ⁱ t rechnet man ² L E

h ρ(E) ⁱ (β) = Z _∞

−∞

dE ρ(E)e ^{− βE} = ^X

n

e ^{− βE}

= ^X

n

e ^{− βE}

Z

Ω

dx ψ _n ^∗ (x)ψ _n (x)

= Z

Ω

dx ^X

n

e ⁻

^E

^t ψ ^∗ _n (x)ψ _n (x)

= Tr K(x ^′ , x, t), wobei L E

h f (E) ⁱ (β) die beidseitige Laplace-Tranformation von f (E) mit dem Parameter β ist. Die Zustandsdichte entspricht also der invers Laplace-Transformierten der Spur des Propagators:

ρ(E) = L ⁻ β ¹

h Tr K(x ^′ , x, t) ⁱ (E). (8) Da die (inverse) Laplace-Transformation linear ist, f¨ uhrt ein Gesamtpropagator der Form K(x ^′ , x, t) = ^P _i λ i K i (x ^′ , x, t) zu einer Zustandsdichte der Form ρ(E) = ^P _i λ i ρ i (E). Das bedeutet, dass jeder Summand im Propagator einzeln betrachtet werden kann.

F¨ ur einen Hamilton-Operator der Form ˆ H = ^P _k H ˆ k mit [ ˆ H k , H ˆ l ] = 0, k¨onnen die L¨ osungen der Schr¨ odingergleichung als Produktzust¨ ande der Form | ψ i = ^N

k | ψ k i ge- schrieben werden, wobei | ψ k i eine L¨ osung der SGL ˆ H k | ψ k i = E k | ψ k i ist. Der Propagator

2

In der Rechnung muss angenommen werden, dass P

n

e

konvergiert. Das ist z.B. f¨ ur t=0 nicht erf¨ ullt. Tats¨ achlich m¨ usste die Funktionenfolge P

n≤N

e

ψ

( x )ψ( x) auf Ω gleichm¨ aßig gegen

K( x , x , t) konvergieren.

2.3. Semiklassische Zustandsdichte

des Systems ist dann

K (x ^′ , x, t) = h x ^′ | e ⁻

^P

^{H ˆ}

| x i = ^Y

k

h x _k ^′ | e ⁻

^{H ˆ}

| x k i = ^Y

k

K(x ^′ _k , x k , t) und die Spur des Propagators ist gegeben durch

Tr K(x ^′ , x, t) = ^Y

k

Tr K (x ^′ _k , x k , t).

Hier sind die x _k Koordinaten in zueinander orthogonalen Unterr¨ aumen, die jeweils zu einem der Hamilton-Operatoren in der Ortsdarstellung geh¨ oren. Der Propagator f¨ ur ein System mit unabh¨angigen orthogonalen Koordinaten kann so zum Beispiel als das Produkt der eindimensionalen Propagatoren geschrieben werden.

2.3. Semiklassische Zustandsdichte

Im semiklassischen Limit wird das Plancksche Wirkungsquantum als klein angesehen, d.h. man betrachtet das asymptotische Verhalten der Quantenmechanik im formalen Grenzfall ~ → 0. Als Beispiel wird hier ein stark verk¨ urzte Darstellung der Herleitung der Gutzwillerschen Spurformel angef¨ uhrt. Diese richtet sich nach [3] und soll nur die grunds¨ atzlichen Ideen aufzeigen. Der Propagator f¨ ur ein System kann immer als ein Pfa- dintegral formuliert werden. Dazu betrachtet man die Propagation eines Teilchens von dem Punkt a zum Punkt b im Konfigurationsraum. Nun wird zuerst ein dritter Punkt c im Konfigurationsraum eingef¨ ugt, der bei der Propagation von a nach b passiert wird und anschließend ¨ uber die Position dieses Punkts integriert. Dieser Vorgang wird formal unendlich oft wiederholt wobei letztendlich ¨ uber alle m¨ oglichen Wege von a nach b inte- griert werden muss. In den Integralen tritt die klassische Wirkung bzw. die Hamiltonsche Prinzipalfunktion f¨ ur jeden Weg mit dem Vorfaktor ¹ _~ als Phase auf. Da ~ sehr klein ist, bewirkt eine kleine ¨ Anderung der Wirkung bereits starke Oszillationen, die sich im In- tegral gegenseitig aufheben. Der Wert des Pfadintegrals ist deshalb haupts¨achlich von den Pfaden mit station¨ arer Phase abh¨ angig. Da nach dem Hamiltonschen Prinzip die klassisch erlaubten Trajektorien genau diejenigen mit station¨ arer Wirkung sind, tragen ebenjene verst¨ arkt zum Wert des Integrals bei. Formal kann deshalb eine Station¨ are- Phasen-N¨aherung im Integral durchgef¨ uhrt werden, bei der nur die klassisch erlaubten Trajektorien ¨ ubrig bleiben. Nach weiteren N¨aherungen bleiben im Zuge der Spurbil- dung bei einer erneuten Station¨ aren-Phasen-N¨ aherung nur die klassischen geschlossenen Phasenraum-Trajektorien ¨ ubrig. Die so erhaltene Spurformel erm¨ oglicht es, die quan- tenmechanische Zustandsdichte nach und nach durch das Hinzunehmen immer l¨ angerer periodischer Bahnen zu approximieren. F¨ ur die k¨ urzeste im weitesten Sinne periodische Bahn der L¨ ange Null kann die Spurformel nicht benutzt werden, jedoch kann deren Beitrag auch ohne Station¨ are-Phasen-N¨aherung berechnet werden. Insgesamt zeigt sich, dass die semiklassische Zustandsdichte in einen mittleren und in einen oszillierenden Anteil aufgespalten werden kann:

ρ(E) = ρ(E) + ρ osz (E).

Dabei kommen die Beitr¨ age zur mittleren Zustandsdichte haupts¨achlich von den Bah- nen der L¨ ange Null. Diese Arbeit besch¨ aftigt sich ausschließlich mit dieser mittleren Zustandsdichte. Deshalb wird der ¨ Uberstrich im Rest der Arbeit weggelassen.

2.4. Freier Propagator und Randkorrekturen

Ein Beispiel f¨ ur ein System mit kontinuierlichem Spektrum ist das freie Teilchen. Der eindimensionale Propagator f¨ ur ein freies Teilchen ist gegeben durch [3]

K 0 (x ^′ , x, t) = r m

2πi ~ t e ⁻

^(x

^{− x)}

. (9) F¨ ur ein Teilchen in einem Gebiet Ω der Dimension D mit dem Kastenpotential U (x) = 0 f¨ ur x ∈ Ω und U (x) = ∞ f¨ ur x / ∈ Ω kann die Zustandsdichte in erster N¨aherung mit Hilfe des freien Propagators berechnet werden. Das kann nach [5] wie folgt begr¨ undet werden: Das mittlere Verhalten von ρ(E) ist bestimmt durch das Verhalten der Laplace- Transformierten (als Funktion von t) bei kleinen Zeiten. In f¨ uhrender Ordnung ist die Zustandsdichte somit durch das Verhalten des Propagators f¨ ur kurze Zeiten bestimmt.

Aus diesem Grund wird angenommen, dass der Einfluss der Berandung S von Ω nur bei den Punkten in ihrer unmittelbaren N¨ahe eine Rolle spielt und bei der Propagation im Innern von Ω vernachl¨ assigt werden kann. Deshalb kann dort der freie Propagator ver- wendet werden, der (in orthogonalen Koordinaten) als das Produkt der eindimensionalen freien Propagatoren geschrieben werden kann. Mit der allgemeinen Identit¨ at

L x

h x ^{ν − 1} Θ(x) ⁱ (τ ) = Z _∞

0 dx x ^{ν − 1} e ^{− τ x} = 1 τ ^ν

Z _∞

0 dx x ^{ν − 1} e ^{− x} = Γ(ν)

τ ^ν (10) f¨ ur Re τ > 0 ergibt sich aus dem freien Propagator die Zustandsdichte

ρ ₀ (E) = L ⁻ β ¹

h Z

Ω

dx K ₀ (x, x, t) ⁱ (E)

= L ⁻ β ¹

h Z

Ω dx m

2π ~ ² β

2

i (E)

= V _Ω m

2π ~ ²

L ⁻ β ¹

h 1 β

i (E)

= V _Ω m

2π ~ ²

E

^{− 1} Γ( ^D ₂ ) Θ(E).

Dabei ist V _Ω das D-dimensionale Volumen des Gebiets Ω und Θ(E) die Heaviside- Funktion. In f¨ uhrender Ordnung ist die Zustandsdichte eines

” freien“Teilchens in einem begrenzten Gebiet also nur vom Volumen des Gebiets und der Energie E abh¨ angig. In dieser Arbeit sind nur die F¨alle D = 1 und D = 2 relevant:

ρ ₀ (E) =



 

 

l 2π

2m

~

_Θ(E)

√ E D = 1

A 4π

2m

~

Θ(E) D = 2

(11)

2.4. Freier Propagator und Randkorrekturen

V = 0

V = ∞

Abbildung 1: Veranschaulichung der f¨ ur die mittlere Zustandsdichte relevanten Trajek- torien. Weit vom Rand entfernt m¨ ussen nur die Trajektorien der L¨ ange Null ber¨ ucksichtigt werden. In unmittelbarer N¨ahe des Randes kommen Reflexionen dazu.

mit der L¨ ange l bzw. der Fl¨ache A.

Um den Einfluss der Berandung S zu ber¨ ucksichtigen, kann die Methode der Spiegel- bilder verwendet werden [5]. Mit der Annahme, dass die Berandung nur bei Punkten in ihrer unmittelbaren N¨ahe eine Rolle spielt, kann diese lokal als Ebene gen¨ ahert werden.

In dieser Arbeit sind die physikalischen Begrenzungen tats¨ achlich durch Punkte oder Strecken gegeben (also Ebenen niedriger Dimension). In dem hier gew¨ ahlten System muss die Wellenfunktion am Rand verschwinden (Dirichlet-Randbedingung). Das be- deutet, dass die Wahrscheinlichkeit f¨ ur die Propagation eines Teilchen auf den Rand null ist. Der Propagator muss also zus¨ atzlich zu (2) f¨ ur x s ∈ S die Bedingung K(x s , · , t) = 0 erf¨ ullen. Ebenfalls wichtig ist der Fall, dass die Normalenableitung der Wellenfunktion auf dem Rand verschwinden muss (Neumann-Randbedingung). Die Bedingung f¨ ur den Propagator ist f¨ ur diesen Fall _∂n ^∂ K(x, · , t) | ^x

= 0. F¨ ur den eindimensionalen Fall mit einer Dirichlet- ( − ) bzw. Neumann-Randbedingung (+) bei x = 0 erf¨ ullt der Propagator

K(x ^′ , x, t) = K ₀ (x ^′ , x, t) ± K ₀ ( − x ^′ , x, t) (12) alle geforderten Eigenschaften. Analog muss in h¨ oheren Dimensionen der freie Propa- gator um den an dem entsprechenden Rand gespiegelten Propagator erg¨ anzt werden.

Anschaulich wird bei der Propagation nun nicht nur der Pfad der L¨ ange Null, sondern

auch der (klassisch erlaubte) Pfad ber¨ ucksichtigt, auf dem das Teilchen am Rand reflek-

tiert wird (siehe Abb. 1). Da angenommen wird, dass die Randbeitr¨ age fast ausschließlich

von der Propagation in unmittelbarer N¨ahe des Randes abh¨ angen, kann die Spurbildung

bei der Koordinate Senkrecht zum Rand bis ins unendliche ausgedehnt werden. Insge-

samt kann gezeigt werden, dass die Zustandsdichte f¨ ur ein beliebiges Gebiet Ω so um

einen Beitrag proportional zur Oberfl¨ ache S erg¨ anzt wird [5]. Dabei k¨onnen die Randkor-

rekturen separat berechnet werden, was die Berechnung stark vereinfachen kann, da das

Koordinatensystem so gew¨ ahlt werden kann, dass die Koordinate senkrecht zur Beran-

dung einer Koordinatenachse entspricht. Die Randkorrektur f¨ ur den eindimensionalen

Fall ergibt sich aus (12) wie folgt:

TrK ₀ ( − x, x, t) = Z _∞

0

dx r m

2πi ~ t e ⁻

^(2x)

= 1 4

Z _∞

−∞

dx r m

2πi ~ t e ⁻

^x

= 1 4

⇒ ρ Rand (E) = ±L ⁻ β ¹

h Tr K ₀ ( − x, x, t) ⁱ (E) = ± 1 4 δ(E),

(13)

wobei die Vorzeichen f¨ ur die Neumann- (+) bzw. Dirichlet-Randbedingung ( − ) stehen.

F¨ ur den zweidimensionalen Fall mit einer Strecke S der L¨ ange l als Begrenzung in x ₂ - Richtung ist der gespiegelte Propagator durch K ^′ (x ^′ , x, t) = K ₀ (x ^′ ₁ , x ₁ , t)K ₀ ( − x ^′ ₂ , x ₂ , t) gegeben und es gilt

TrK ^′ (x ^′ , x, t) = Z

S

dx ₁ Z _∞

0

dx ₂ m

2πi ~ t e ⁻

^(2x

⁾

= l 4

r m 2π ~ ² β

⇒ ρ Rand (E) = ±L ⁻ β ¹

h T rK R (x ^′ , x, t) ⁱ (E) = ± l 8π

2m

~ ²

2

Θ(E)

√ E .

(14)

F¨ ur gekr¨ ummte Berandungen kann auch ein weiterer von der Kr¨ ummung abh¨ angiger Beitrag hergeleitet werden. Dieser ist jedoch f¨ ur diese Arbeit nicht relevant. Stattdessen werden an mehreren Stellen Eck-Korrekturen berechnet. Diese ergeben sich prinzipiell wieder aus Spiegelungen des Propagators an den beteiligten R¨ andern.

2.5. Vielteilchen-Propagator

Da in dieser Arbeit ein System aus zwei Teilchen betrachtet wird, ist es sinnvoll die Eigen- schaften eines Zweiteilchen-Propagators allgemein zu charakterisieren. F¨ ur ein besseres Verst¨ andnis werden diese Eigenschaften hier f¨ ur beliebig viele Teilchen hergeleitet. Ge- geben sei ein System aus N identischen Teilchen in D Dimensionen. Die Gesamtwellen- funktionen f¨ ur ein solches System muss antisymmetrisch (Fermionen) oder symmetrisch (Bosonen) sein. Das entspricht dem Umstand, dass die Teilchen quantenmechanisch nicht unterscheidbar sind. Die antisymmetrischen bzw. symmetrischen L¨ osungen der Schr¨ odinger-Gleichung bilden einen Unterraum des gesamten Hilbertraums. Der Projek- tionsoperator auf diesen Unterraum kann f¨ ur die Teilchenkoordinaten x := (x ₁ , . . . , x N ) im Konfigurationsraum Ω ^N direkt angegeben werden. Um diesen zu vereinfachen wird der Begriff der fundamentalen Dom¨ ane eingef¨ uhrt: Die Gruppe S _N der Permutationen

¨

uber { 1, . . . , N } operiert auf der Menge Ω ^N gem¨ aß P (x ₁ , · · · , x N ) = (x _{P (1)} , · · · , x _{P (N)} ).

Die Bahnen S N x = { P x | P ∈ S N } der Elemente x ∈ Ω ^N unter S N sind entweder dis- junkt oder gleich. Eine fundamentale Dom¨ ane F wird definiert als ein Vertretersystem der Bahnen in Ω ^N unter S _N . Im folgenden werden zur Vereinfachung nur Zust¨ande be- trachtet, bei denen x i 6 = x j f¨ ur beliebige Indices i, j ∈ { 1, . . . , N } , i 6 = j gilt. Sind x und x ^′ zwei Vertreter der selben Bahn, so legen sie (bis auf Vorzeichen) den gleichen symmetrischen (+) bzw. antisymmetrischen ( − ) Zustand

| x i ^± := 1

√ N ! X

P ∈ S

( ± ) ^P | P x i (15)

2.5. Vielteilchen-Propagator fest. Durch die Beschr¨ ankung auf die Fundamentale Dom¨ ane liefert diese Beziehung eine Bijektion zwischen dem Unterraum der (anti-)symmetrischen Zust¨ande und der Funda- mentalen Dom¨ ane. Außerdem sind f¨ ur verschiedene Elemente x, x ^′ ∈ F die durch (15) festgelegten Zust¨ande orthogonal. Der Projektions-Operator ist damit gegeben durch

P ˆ _± = Z

F

dx ^{N D} | x i ^± h x | ^± = Z

F

dx ^{N D} 1 N !

X

P,Q ∈ S

( ± ) ^{P ◦ Q} | P x i h Qx | . (16) F¨ ur einen beliebigen Zustand | x ^′ i mit x ^′ ∈ Ω ^N existiert nun ein eindeutiges R ∈ S N mit Rx ^′ ∈ F Also gilt

P ˆ _± | x ^′ i = Z

F

dx ^{N D} 1 N !

X

P ∈ S

( ± ) ^{P ◦ R}

| P x i δ(R ^{− 1} x − x ^′ )

= 1 N !

X

P ∈ S

( ± ) ^{P ◦ R} | P ◦ Rx ^′ i

= 1 N !

X

P ∈ S

( ± ) ^P | Px ^′ i

unabh¨angig von R. Dabei wurde benutzt, dass sgn(P ^{− 1} ) = sgn(P ) gilt und S N transitiv auf sich selbst operiert. Die Summation ¨ uber die Permutationen Q ist damit ¨ aquivalent zur Ausweitung der Integration auf Ω ^N :

P ˆ _± = Z

Ω

dx ^{N D} 1 N !

X

P ∈ S

( ± 1) ^P | P x i h x | (17) Dieser Projektionsoperator ist auch f¨ ur beliebige Zust¨ande mit evtl. nicht paarweise verschiedenen Teilchenkoordinaten verwendbar. Das kann leicht mit einem beliebigen Zustand verifiziert werden. Die Herleitung erfordert lediglich etwas mehr Schreibaufwand und die Verwendung der Isotropiegruppe { P ∈ S N | P x = x } von x.

Als Projektionsoperator ist ˆ P _± idempotent und hermitesch. Außerdem kommutiert er wegen [ ˆ P _± , H ˆ ] = 0 mit dem Zeitentwicklungsoperator ˆ U (t). Deshalb ist der Propagator f¨ ur das System durch

K _± (x ^′ , x, t) = h x ^′ | P ˆ _± U ˆ (t) ˆ P _± | x i = h x ^′ | P ˆ _± U ˆ (t) | x i (18) gegeben. Ist der Propagator f¨ ur N identische unterscheidbare Teilchen gegeben durch K(x ^′ , x, t), so erh¨ alt man den Propagator f¨ ur das System aus N identischen ununter- scheidbaren Teilchen (also Bosonen (+) oder Fermionen ( − )) daraus also wie folgt:

K _± (x ^′ , x, t) = 1 N !

X

P ∈ S

( ± ) ^P K(P x ^′ , x, t). (19) Dabei sind x und x ^′ beliebige Teilchenkonfigurationen. Eine Spurbildung erfolgt deshalb

¨

uber den gesamten Konfigurationsraum Ω ^N . In manchen F¨allen ist es sinnvoll die Inte-

gration nicht ¨ uber den gesamten Konfigurationsraum auszudehnen, sondern nur die fun-

damentale Dom¨ ane zu betrachten. Nimmt man wieder paarweise verschiedene Teilchen-

koordinaten an, so besteht jede Bahn aus genau N ! Elementen. Der Propagator f¨ ur die

x ₁ x 2

F 2

L L

0

Abbildung 2: Fundamentale Dom¨ ane F 2 f¨ ur das System aus zwei Teilchen auf einer Linie der L¨ ange L.

fundamentale Dom¨ ane muss mit N ! multipliziert werden, da diese Mehrfachz¨ ahlungen nun wegfallen. Anders ausgedr¨ uckt: der Vorfaktor _N! ¹ korrigiert die Mehrfachz¨ ahlungen bei der Integration ¨ uber den gesamten Konfigurationsraum.

In dieser Arbeit ist vor allem eine spezielle fundamentale Dom¨ ane f¨ ur zwei Teilchen auf einer Linie der L¨ ange L von Interesse. Diese kann in der Form F 2 = { x ∈ [0, L] ² | x ₂ ≤ x ₁ } angegeben werden und ist in Abb. 2 graphisch dargestellt. Der freie Propagator f¨ ur zwei unterscheidbare identische Teilchen auf einer Geraden kann als das Produkt der eindimensionalen Propagatoren geschrieben werden. Der auf die fundamentale Dom¨ ane beschr¨ ankte (anti-)symmetrische Propagator f¨ ur die ununterscheidbaren Teilchen ist des- halb (ohne Randkorrekturen) gegeben durch

K _± (x ^′ , x) = K ₀ (x ^′ ₁ , x ₁ )K ₀ (x ^′ ₂ , x ₂ ) ± K ₀ (x ^′ ₂ , x ₁ )K ₀ (x ^′ ₁ , x ₂ ).

Das entspricht aber genau dem Propagator f¨ ur ein Teilchen in zwei Dimensionen mit einer Neumann- bzw. Dirichlet-Randkorrektur bei x 1 = x 2 . Das System aus zwei unun- terscheidbaren Teilchen auf einer Strecke der L¨ ange L ist deshalb ¨ aquivalent zu einem System aus einem (virtuellen) Teilchen in dem zweidimensionalen Gebiet G = F 2 mit einer Neumann-Randbedingung f¨ ur Bosonen bzw. einer Dirichlet-Randbedingung f¨ ur Fermionen (siehe hierzu auch [6]).

2.6. Lokale Zustandsdichte f¨ ur eindimensionale Systeme

Die Lokale Zustandsdichte enth¨ alt zus¨ atzlich zur Information ¨ uber das Spektrum auch Informationen ¨ uber die Aufenthaltswahrscheinlichkeit der Teilchen. F¨ ur ein Teilchen auf einer Linie der L¨ ange L ist sie gegeben durch

ρ(x, E) = ^X

n

δ(E − E n ) | ψ n (x) | ² = L ⁻ _β ^{1 h} K(x, x, t = − i ~ β) ⁱ (E), (20)

d.h. die Integration bei der Spurbindung des Propagators wird weggelassen. F¨ ur mehrere

Teilchen ist man lediglich daran interessiert, mit welcher Wahrscheinlichkeit man in

2.6. Lokale Zustandsdichte f¨ ur eindimensionale Systeme einem Gebiet mindestens ein Teilchen findet, wobei die Position der anderen Teilchen keine Rolle spielt. Diese Information bleibt erhalten, wenn man bei der Spurbildung die Integration ¨ uber genau eine Teilchenkoordinate ausl¨ asst. Sind die Wellenfunktionen gegeben durch ψ n (x) so erh¨ alt man die lokale Zustandsdichte durch

ρ(x, E) = L ⁻ β ¹

h Z

L

dx ^{N − 1} K(x, x, t) ⁱ (E)

= ^X

n

δ(E − E _n ) Z

L

dx ^{n − 1} | ψ _n (x) | ²

= ^X

n

δ(E − E n ) n n (x) N

mit der ¨ uber N − 1 Teilchenkoordinaten gemittelten Teilchendichte n n (x) = N

Z

L

dx ^{N − 1} | ψ n (x) | ² . (21) Diese gibt den Erwartungswert f¨ ur die Anzahl der Teilchen an, die man in einem infi- nitesimalen Intervall auf der Linie antrifft. F¨ ur ein Kontinuierliches Spektrum wird die Teilchendichte zu n(E, x). In diesem Fall erh¨ alt man sie aus der lokalen Zustandsdichte mit Hilfe der Normierungsbedingung

Z _L

0

dx n(x, E) = N, wobei n(x, E) = A(E) · ρ(x, E) gelten muss. Das liefert

n(x, E) = N

ρ(E) ρ(x, E).

Dabei ist ρ(x) die (globale) Zustandsdichte ³ .

3

Schreibt man f¨ ur ein diskretes System δ(E − E

) = lim

δ

(E − E

) mit Diracfolgen δ

, so gilt die

Formel auch f¨ ur diesen Fall.

− L 0 L αδ

Abbildung 3: Potentialtopf mit δ-Barriere. Die erste symmetrische und die erste anti- symmetrische L¨ osung (f¨ ur α > 0) sind eingezeichnet.

3. Herleitung des Propagators f¨ ur ein Deltapotential

In diesem Abschnitt soll der Propagator f¨ ur ein Teilchen der Masse m auf einer unendlich ausgedehnten Linie mit einem Potential der Form U (x) = αδ(x) (sprich Deltapotential bei x = 0 der St¨ arke α) hergeleitet werden. Dabei ist α ein beliebiger reeller Parameter.

Dazu werden zuerst die L¨ osungen der Schr¨ odingergleichung f¨ ur ein beschr¨ anktes System der L¨ ange 2L berechnet, um dann den gesuchten Propagator aus dem Grenz¨ ubergang L → ∞ zu erhalten. Um die Ergebnisse der folgenden Abschnitte ¨ ubersichtlicher schrei- ben zu k¨onnen, werden an dieser Stelle zwei α-abh¨ angige Gr¨ oßen definiert:

κ := mα

~ ² , (22)

µ := ~ ² κ ²

2m . (23)

Dabei hat κ die Dimension einer Wellenzahl und µ die einer Energie. Ab Abschnitt 4.2 wird ein Einheitensystem gew¨ ahlt, in dem _2m ^~

= 1 gilt. In diesem Fall vereinfachen sich obige Beziehungen zu

κ = α

2 , µ = κ ² .

3.1. Exakte L¨ osungen f¨ ur den Potentialtopf mit Delta-Barriere

Gegeben sei ein unendlicher Potentialtopf der Breite 2L symmetrisch zum Ursprung (vgl.

Abb. 3). In der Mitte des Topfes befinde sich ein δ-Potential der Form U (x) = αδ(x) der St¨ arke α ∈ R . Der Hamiltonoperator in Ortsdarstellung ist dann f¨ ur x ∈ [ − L, L]

gegeben durch

H ˆ = − ~ ² 2m

∂ ²

∂x ² + αδ(x). (24)

Die L¨ osungen der Schr¨ odingergleichung ˆ H ψ(x) = Eψ(x) m¨ ussen im Ursprung stetig sein. Weiter gilt:

ǫ lim → 0 ψ ^′ (ǫ) − ψ ^′ ( − ǫ) = lim

ǫ → 0

Z _ǫ

− ǫ

dx ψ ^′′ (x)

SGL

= lim

ǫ → 0

Z ǫ

− ǫ

dx − 2m

~ ² (E − αδ(x))ψ(x)

= 2mα

~ ² ψ(0).

Da das System symmetrisch zum Ursprung ist, sind alle station¨ aren L¨ osungen entweder symmetrisch oder antisymmetrisch. F¨ ur die antisymmetrischen L¨ osungen folgt aus der Stetigkeit ψ(0) = 0. F¨ ur diese ist obige Bedingung also ¨ aquivalent zur Stetigkeit der Ableitung im Ursprung. Die antisymmetrischen L¨ osungen werden also von der δ-Barriere nicht beeinflusst und entsprechen genau den bekannten antisymmetrischen L¨ osungen f¨ ur einen unendlichen Potentialtopf. Sie sind gegeben durch

ψ ⁻ _n (x) = 1

√ L sin(k ⁻ _n x) k ⁻ _n = nπ

L , n ∈ N . (25)

F¨ ur die symmetrischen L¨ osungen folgt mit der Definition (22) f¨ ur die rechtsseitige Ab- leitung im Ursprung die Bedingung

ψ ^′ (0 ⁺ ) = κ · ψ(0). (26)

F¨ ur κ = 0 ergibt dies eine Neumann-Randbedingung, w¨ ahrend der Grenzfall κ → ∞ nur f¨ ur ψ(0) = 0, also Dirichlet-Randbedingungen, erf¨ ullt werden kann. Deshalb spricht man bei einer Randbedingung der Form (26) von einer gemischten Randbedingung.

Im Folgenden wird zuerst nur α ≥ 0 bzw. ¨ aquivalent κ ≥ 0 betrachtet. Der Fall κ < 0 wird am Ende des Abschnitts separat behandelt.

Der Ansatz ψ(x) = A sin(k( | x | − L)) erf¨ ullt die Randbedingungen ψ( − L) = ψ(L) = 0 und f¨ ur die Ableitung gilt ψ ^′ (x) = sgn(x)Ak cos(k( | x | − L)). Die Bedingung (26) liefert dann

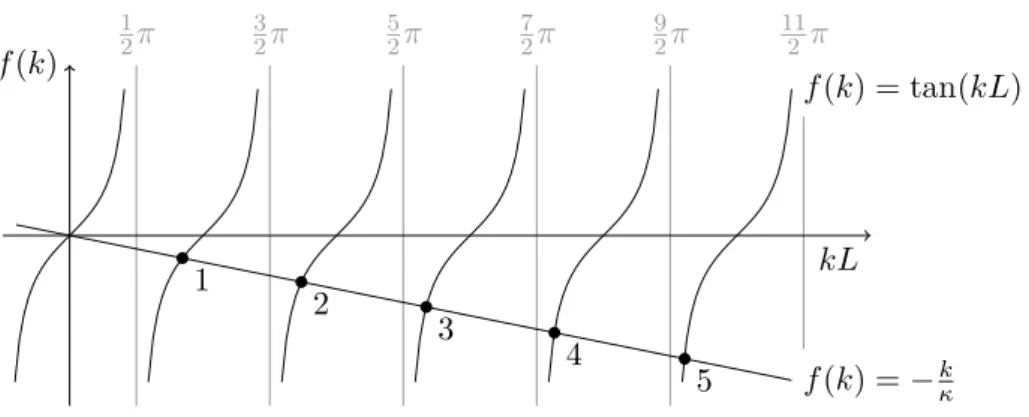
tan(kL) = − k

κ . (27)

Dies ist eine transzendente Gleichung mit jeweils einer L¨ osung f¨ ur kL in jedem Intervall (nπ − ^π ₂ , nπ + ^π ₂ ) mit n ∈ Z (vgl. Abb. 4). Dabei ist f¨ ur jede L¨ osung k n auch − k n eine L¨ osung, liefert aber keine linear unabh¨angige Wellenfunktion ψ. Außerdem ist f¨ ur k = 0 die Wellenfunktion ψ identisch Null. Deshalb kann man sich auf n ∈ N beschr¨ anken ⁴ . Nach der Normierung auf dem Intervall [ − L, L] ergeben sich die symmetrischen L¨ osungen zu

ψ ⁺ _n (x) = 1

√ L 1 − sin(2k ⁺ _n L) 2k ⁺ n L

! ₋

sin k _n ⁺ ( | x | − L) k ⁺ _n = − κ tan(k _n ⁺ L), mit k _n ⁺ L ∈ (nπ − π

2 , nπ + π 2 )

(28)

3.2. Propagator f¨ ur eine Delta-Barriere

1

2 π ³ ₂ π ⁵ ₂ π ⁷ ₂ π ⁹ ₂ π ¹¹ ₂ π

kL f (k)

f (k) = − ^k _κ f (k) = tan(kL)

1 2

3 4

5

Abbildung 4: Graphische L¨ osungen der transzendenten Gleichung tan(kL) = − ^k _κ f¨ ur κ > 0. In jedem Intervall (nπ − ^π ₂ , nπ + ^π ₂ ) existiert genau eine L¨ osung.

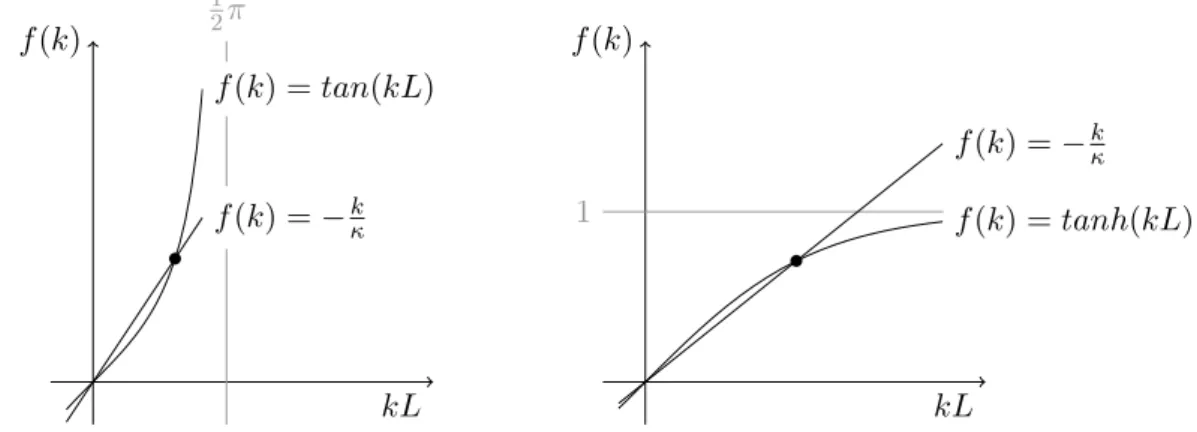
Die obige Herleitung ist auch f¨ ur den Fall κ < 0 g¨ ultig, weshalb die Wellenfunktionen in (28) auch f¨ ur κ < 0 L¨ osungen darstellen. Allerdings existiert f¨ ur κL ∈ ( − 1, 0) eine weitere L¨ osung k ₀ der Gleichung (27) mit k ₀ L ∈ (0, ^π ₂ ). Es gibt jedoch nicht nur f¨ ur κL ∈ ( − 1, 0) eine zus¨ atzliche L¨ osung: der Ansatz ψ(x) = A sinh(k( | x | − l)) erf¨ ullt ebenfalls die Randbedingung ψ( ± L) = 0. Aus (26) ergibt sich die transzendente Gleichung

tanh(kL) = − k

κ . (29)

Diese Gleichung hat f¨ ur κL ∈ ( −∞ , − 1) eine nicht verschwindende L¨ osung k ₀ ^′ . Aufgrund der Symmetrie kann wieder die positive L¨ osung gew¨ ahlt werden. Setzt man den Ansatz in die Schr¨ odingergleichung ein, so zeigt sich, dass die zugeh¨ orige Energie negativ sein muss. Tats¨ achlich geht der hier gew¨ ahlte Ansatz aus dem urspr¨ unglichen Ansatz durch die Ersetzung (k → ik), also einer imagin¨ aren Frequenz, hervor ⁵ . Die Normierung liefert die Wellenfunktion

ψ ₀ ⁺ (x) = 1

√ L

sinh(2k ₀ ^′ L) 2k ^′ ₀ L − 1

₋

sinh(k ^′ ₀ ( | x | − L)). (30) Die zus¨ atzlichen L¨ osungen der transzendenten Gleichungen (27) und (29) sind in Abb.

5 graphisch dargestellt. F¨ ur κL = − 1 gibt es keine weitere L¨ osung. Dieser Fall ist aber vernachl¨ assigbar.

3.2. Propagator f¨ ur eine Delta-Barriere

Im dem vorhergehenden Unterkapitel wurden die exakten (reellen) L¨ osungen f¨ ur das beschr¨ ankte Problem berechnet. Der Propagator f¨ ur dieses System ist damit gegeben

4

Es gibt verschiedene Konventionen f¨ ur die nat¨ urlichen Zahlen N . In dieser Arbeit ist 0 ∈ / N

5

Damit kann diese L¨ osung als innerhalb des Potentialtopfs gebundener Zustand angesehen werden.

kL f (k)

1 2 π

f (k) = − ^k _κ f (k) = tan(kL)

kL f (k)

1

f (k) = − ^k _κ f (k) = tanh(kL)

Abbildung 5: Zus¨atzliche L¨ osungen f¨ ur κ < 0. Links: positive L¨ osung der Gleichung tan(kL) = − ^k _κ f¨ ur κL > − 1. Rechts: L¨ osung der Gleichung tanh(kL) = − ^k _κ f¨ ur κL < − 1.

durch

K _{⌊ δ ⌋} (x ^′ , x, t) = X ∞

n=1

e ⁻

^(k

⁾

ψ _n ⁺ (x ^′ )ψ _n ⁺ (x) + X ∞

n=1

e ⁻

^(k

⁾

ψ _n ⁻ (x ^′ )ψ _n ⁻ (x).

F¨ ur κ < 0 m Um den Propagator f¨ ur das unbeschr¨ ankte System zu erhalten, muss der Grenz¨ ubergang L → ∞ durchgef¨ uhrt werden. Dazu werden zuerst die symmetrischen L¨ osungen des beschr¨ ankten Systems f¨ ur große Werte von L gen¨ ahert. Die mit n = 0 indizierten L¨ osungen f¨ ur κ < 0 werden am Ende dieses Abschnitts separat behandelt.

Bis dahin gilt n ∈ N . F¨ ur großes L vereinfachen sich die Wellenfunktionen in (28) zu ψ _n ⁺ (x) ≈ 1

√ L sin k n ( | x | − L) (31) und man erh¨ alt (Herleitung im Anhang, Indices weggelassen)

ψ ⁺ (x ^′ )ψ ⁺ (x) = 1 2L

"

cos k(x ^′ + x) + cos k(x ^′ − x) − 2 Re e ^{ik( | x}

^{| + | x | )} 1 + i _κ ^k

#

. (32) Bemerkenswert an dieser Darstellung ist, dass Λ ⁺ (k, x ^′ , x) := L · ψ ⁺ (x ^′ )ψ ⁺ (x) nicht mehr explizit von der Ausdehnung L des Systems abh¨ angt. Implizit ist jedoch k von L abh¨ angig. F¨ ur große Werte von L kann diese Abh¨ angigkeit stark vereinfacht werden.

Gleichung (27) ergibt mit der Ersetzung u := kL die Gleichung tan(u) = − _κL ^u . Im Grenzfall L → ∞ sind die L¨ osungen dieser Gleichung gegeben durch u n = k n L = nπ und damit

k n = nπ

L . (33)

Die Differenz k _n+1 − k n = ^π _L nimmt mit L ab, d.h. die k n r¨ ucken immer n¨ aher zusammen.

Formal gilt f¨ ur beliebige n ∈ N

L lim →∞ L(k n+1 − k n ) = π. (34)

3.2. Propagator f¨ ur eine Delta-Barriere Außerdem konvergiert k 1 gegen Null. Damit k¨onnen wir den symmetrischen Anteil des Propagators f¨ ur das unbeschr¨ ankte System in geschlossener Form angeben als

K _δ ⁺ (x ^′ , x, t) = lim

L →∞

X ∞

n=1

e ⁻

^k

^t ψ _n ⁺ (x ^′ )ψ _n ⁺ (x)

= lim

L →∞

X ∞

n=1

(k _n+1 − k n ) · e ⁻

^k

^t Λ ⁺ (k n , x ^′ , x) · 1 L(k _n+1 − k n )

= Z _∞

0 dk e ⁻

^k

^t Λ ⁺ (k, x ^′ , x) 1 π

= 1 2π

Z _∞

−∞ dk e ⁻

^k

^t Λ ⁺ (k, x ^′ , x).

Dabei wurde die Definition des Riemannschen Integrals mit der Zerlegung der positiven k-Achse in Intervalle [k n , k n+1 ) verwendet, sowie im letzten Schritt die Symmetrie des Integranden bez¨ uglich k ausgenutzt.

F¨ ur die antisymmetrischen L¨ osungen (25) gilt sogar f¨ ur endliche L¨ angen L f¨ ur alle n ∈ N : L(k _n+1 − k _n ) = π. Ersetzt man in obiger Herleitung ψ ⁺ (x ^′ )ψ ⁺ (x) durch

ψ ⁻ (x ^′ )ψ ⁻ (x) = 1

L sin(kx ^′ ) sin(kx) = 1 2L

cos(k(x ^′ − x)) − cos(k(x ^′ + x))

und definiert entsprechend Λ ⁻ := Lψ ⁻ (x ^′ )ψ ⁻ (x), so erh¨ alt man bis auf Indizierung den gleichen Ausdruck f¨ ur den antisymmetrischen Anteil. Insgesamt folgt

K δ (x ^′ , x, t) = 1 2π

Z _∞

−∞

dk e ⁻

^k

^t Λ ⁺ (k, x ^′ , x) + 1 2π

Z _∞

−∞

dk e ⁻

^k

^t Λ ⁻ (k, x ^′ , x)

= 1 2π

Z _∞

−∞ dk e ⁻

^k

^t cos k(x ^′ − x) − 1 2π

Z _∞

−∞ dk e ⁻

^k

^t Re e ^{ik( | x}

^{| + | x | )} 1 + i ^k _κ . An dieser Stelle kann der Spezialfall α = 0 bzw. κ = 0 betrachtet werden, der den freien Propagator liefern sollte. Dazu muss lediglich folgender Grenzwert berechnet werden (z = | x ^′ | + | x | ):

κ lim → 0 Re e ^ikz

1 + i ^k _κ = lim

κ → 0

cos(kz) + ^k _κ sin(kz) 1 + ( ^k _κ ) ² = lim

κ → 0

κ ² cos(kz) + κ sin(kz) κ ² + k ² = 0 Der Propagator ist f¨ ur κ = 0 mit der Abk¨ urzung d := x ^′ − x gegeben durch:

K δ (x ^′ , x, t)

κ=0 = 1 2π

Z _∞

−∞

dk e ⁻

^k

^t cos(kd)

= 1 4π

Z _∞

−∞ dk e ⁻

^k

(e ^ikd + e ^{− ikd} )

= 1

4π e ⁻

^d

Z _∞

−∞ dk e ⁻

^{(k −}

⁾

+ e ⁻

^(k+

⁾

= 1

2π e ⁻

^d

Z _∞

−∞ dk e ⁻

^k

= r m

2πi ~ t e ⁻

^d

und stimmt mit dem bekannten Ausdruck f¨ ur den freien Propagator ¨ uberein. F¨ ur κ 6 = 0 kann das zweite Integral in K δ nicht auf elementare Funktionen reduziert werden. Es kann jedoch in eine einfachere Form gebracht werden. Dazu substituiert man z := | x ^′ | +

| x | und betrachtet das Integral I(ǫ) := 1

2π Z _∞

−∞

dk e ⁻

^k

^t Re e ^ik(z+ǫ)

1 + i ^k _κ . (35)

F¨ ur ǫ = 0 entspricht es genau dem gesuchten Integral in K _δ . Wegen

| I (ǫ) | ≤ 1 2π

Z _∞

−∞

dk

e ⁻

^k

^t Re e ^ik(z+ǫ) 1 + i ^k _κ

≤ 1

2π Z _∞

−∞

dk 1

1 + ( ^k _κ ) ² = κ

2 (36)

ist es f¨ ur beliebige ǫ ∈ R beschr¨ ankt. Weiter erf¨ ullt es die Differentialgleichung ( ∂

∂ǫ − κ)I (ǫ) = − κ Z _∞

−∞

dk e ⁻

^k

^t cos(k(z + ǫ))

= − κ r m

2πi ~ t e ⁻

^(z+ǫ)

=: f (ǫ).

Die homogene L¨ osung dieser Differentialgleichung ist I ₀ (ǫ) = ae ^κǫ mit einem zun¨ achst unbekannten komplexen Parameter a. Sei nun κ ≥ 0. Die Greensche Funktion

G(ǫ) := − Θ( − ǫ)e ^κǫ

ist eine spezielle L¨ osungen der Differentialgleichung ( _∂ǫ ^∂ − κ)G(ǫ) = δ(ǫ). Die Faltung von G mit f liefert eine spezielle L¨ osung der Differentialgleichung f¨ ur I(ǫ). Die allgemeinen L¨ osungen sind also gegeben durch

I (ǫ) = I 0 (ǫ) + (G ∗ f )(ǫ)

= I ₀ (ǫ) + κ Z _∞

−∞

dǫ ^′ Θ(ǫ ^′ − ǫ)e ^{κ(ǫ − ǫ}

⁾ r m

2πi ~ t e ⁻

^(z+ǫ

⁾

= ae ^κǫ + κ r m

2πi ~ t e ^κǫ Z _∞

ǫ

dǫ ^′ e ^{− κǫ}

e ⁻

^(z+ǫ

⁾

mit dem noch zu bestimmenden (eventuell von κ abh¨ angenden) Parameter a. F¨ ur κ → 0 muss f¨ ur beliebige ǫ ∈ R I (ǫ) → 0 erf¨ ullt sein. Das l¨ asst schon a = 0 vermuten.

Tats¨ achlich muss I (ǫ) beschr¨ ankt sein. Das Integral auf der rechten Seite ist f¨ ur jedes ǫ ∈ R beschr¨ ankt durch

κ

r m 2πi ~ t

Z _∞

0

dǫ ^′ e ^{− κǫ}

e ⁻

^(z+ǫ

^+ǫ) ≤

r m

2π ~ t , (37)

w¨ ahrend die homogene L¨ osung ae ^κǫ f¨ ur a 6 = 0 unbeschr¨ ankt ist. Daraus folgt a = 0. Der Propagator f¨ ur eine Deltabarriere ist f¨ ur κ ≥ 0 damit gegeben durch

K _δ (x ^′ , x, t) = K ₀ (x ^′ , x, t) − κ r m

2πi ~ t Z _∞

0

dǫ e ^{− κǫ} e ⁻

^{( | x}

^{| + | x | +ǫ)}

. (38)

3.2. Propagator f¨ ur eine Delta-Barriere Dies ist kein neues Ergebnis. In [8] wird dieser Propagator ¨ uber die quantenmechani- sche Greensche Funktion hergeleitet. Dort wird jedoch κ > 0 vorausgesetzt. F¨ ur κ < 0 konvergiert das Integral auf der rechten Seite jedoch nicht. Dieses Problem wird durch die Verwendung einer anderen Greenschen Funktion gel¨ ost: durch Addieren von e ^κǫ zu G erh¨ alt man die Greensche Funktion

G ^′ (ǫ) := Θ(ǫ)e ^κǫ .

Durch die Faltung von G ^′ mit f erh¨ alt man die allgemeine L¨ osung f¨ ur κ < 0 I (ǫ) = ae ^κǫ − κ

Z _∞

−∞

dǫ ^′ Θ(ǫ − ǫ ^′ )e ^{κ(ǫ − ǫ}

⁾ r m

2πi ~ t e ⁻

^(z+ǫ

⁾

= ae ^κǫ − κ r m

2πi ~ t e ^κǫ Z _∞

− ǫ

dǫ ^′ e ^κǫ

e ⁻

^{(z − ǫ}

⁾

.

Analog folgt auch hier a = 0. In Abschnitt 3.1 wurde f¨ ur κ < 0 abh¨ angig vom Betrag von κL eine weitere L¨ osung gefunden, f¨ ur die nun der Grenzfall L → ∞ betrachtet wird. F¨ ur ausreichend große L¨ angen L ist κL < − 1 erf¨ ullt und die Wellenfunktion des Zustands ist gegeben durch

ψ ⁺ ₀ (x) = 1

√ L

sinh(2k ₀ L) 2k 0 L − 1

₋

sinh(k ₀ ( | x | − L)) = ^p 2k ₀ sinh(k ₀ ( | x | − L)) p sinh(2k 0 L) − 2k 0 L . Die L¨ osung von (29) ist im Grenzfall L → ∞ wegen lim L →∞ tanh(kL) = Θ(k) − Θ( − k) durch k = − κ = | κ | gegeben. Außerdem ist aus der graphischen Betrachtung leicht ersichtlich, dass mit wachsender L¨ ange L auch die L¨ osung von (29) gr¨ oßer wird. Im Limes kann also ohne Beschr¨ ankung der Allgemeinheit k ∈ [ ^{| κ} ₂ ^| , | κ | ] angenommen werden.

Damit ist die folgende Grenzwertbildung gerechtfertigt:

L lim →∞ ψ ⁺ ₀ (x) = lim

L →∞

√ 2k sinh(k( | x | − L)) p sinh(2kL) − 2kL

= lim

L →∞

√ k e ^{k( | x |− L)} − e ^{− k( | x |− L)}

√ e ^2kL − e ^{− 2kL} − 4kL

= lim

L →∞

√ k e ^{k | x |} e ^{− 2kL} − e ^{− k | x |}

√ 1 − e ^{− 4kL} − 4kLe ^{− 2kL}

= − ^q | κ | e ^{κ | x |} .

Das ist die L¨ osung der Schr¨ odingergleichung f¨ ur das unbeschr¨ ankte System mit einer δ-Barriere bei x = 0 mit der Energie E 0 = − _2m ^~

κ ² = − µ (siehe (23)). Nun kann der Propagator f¨ ur das Unbeschr¨ ankte System auch f¨ ur negative Werte von κ angegeben werden:

K δ (x ^′ , x, t) = K ₀ (x ^′ , x, t) + κ r m

2πi ~ t Z _∞

0 dǫ e ^κǫ e ⁻

^{( | x}

^{| + | x |− ǫ)}

− κe

^µt e ^{κ( | x}

^{| + | x | )} .

F¨ ur beliebige Werte von κ kann der Propagator folgendermaßen geschrieben werden:

K _δ (x ^′ , x, t) = K ₀ (x ^′ , x, t) − | κ | r m

2πi ~ t Z _∞

0

dǫ e ^{−| κ | ǫ} e ⁻

^{( | x}

^{| + | x | +sgn(κ)ǫ)}

+ Θ( − κ) | κ | e

^µt e ^{−| κ | ( | x}

^{| + | x | )} .

(39)

Das ist ein fundamentales Ergebnis, das f¨ ur die folgenden Abschnitte ben¨ otigt wird. Zum Zwecke der ¨ Ubersichtlichkeit wird in den folgenden Abschnitten in Einheiten gearbeitet, f¨ ur die _2m ^~

= 1 gilt. Die Zeitabh¨angigkeit der Propagation wird in die rein imagin¨ are Gr¨ oße β = _~ ⁱ t integriert (β ist die ¨ uber die Laplace-Transformation zu E konjugierte Variable). Der freie Propagator vereinfacht sich damit zu

K ₀ (x ^′ , x, t) = 1

√ 4πβ e

^(x

^{− x)}

. F¨ ur die folgenden Abschnitte wird außerdem die Abk¨ urzung

K κ (x ^′ , x, t) := − κ 1

√ 4πβ Z _∞

0 dǫ e ^{− κǫ} e ⁻

^{( | x}

^{| + | x |± ǫ)}

+ θ ⁰ ₁ κe ^µβ e ^{− κ( | x}

^{| + | x | )}

eingef¨ uhrt. In dieser Darstellung wird κ mit | κ | identifiziert und die Fallunterscheidung erfolgt durch die unterschiedlichen Vorzeichen. Das obere Zeichen steht ab hier immer f¨ ur ein positives Potential (κ ≥ 0) und das untere f¨ ur ein negatives Potential (κ < 0).

Der Vorfaktor des zweiten Summanden ist definiert als θ ⁰ ₁ :=

( 0 κ ≥ 0

1 κ < 0.