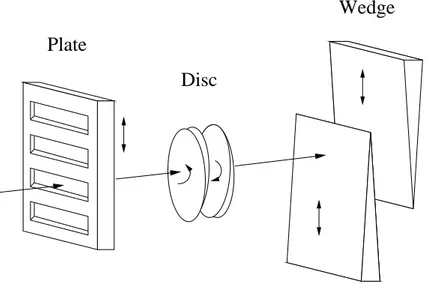
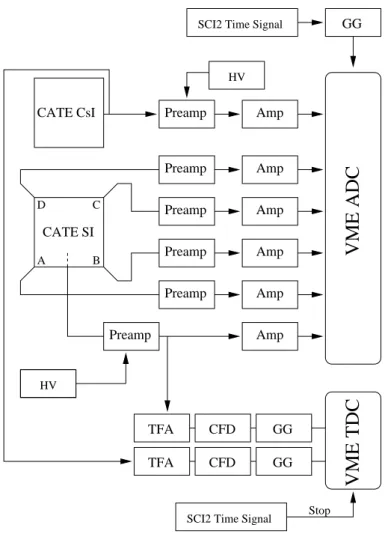
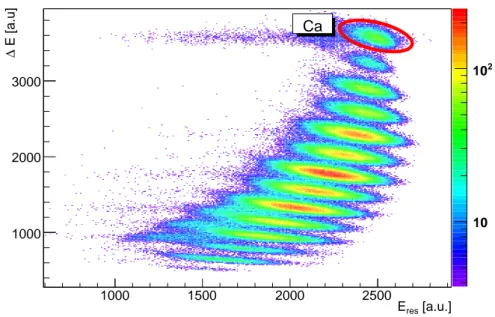
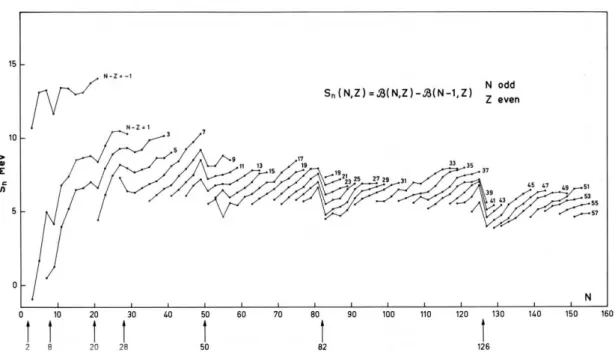
In-beam γ-ray spectroscopy of two-step fragmentation reactions at relativistic energies — The case of
Volltext
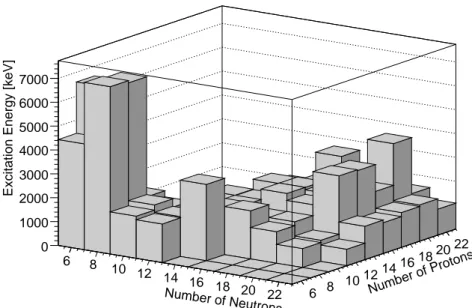
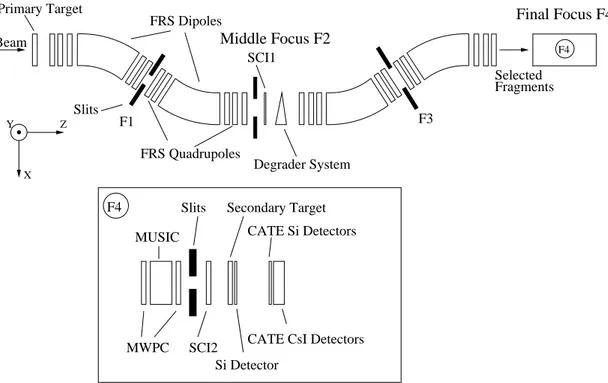
Abbildung

ÄHNLICHE DOKUMENTE
The observed mismatch may be explained by the fact that the model was trained heavily with biochar sorbents of relatively low S BET (83% datasets with S BET < 400 m 2 /g) as
significantly change, as inhibition of methanogens using 2-BES prevents loss of biofilm activity 349. or biofilm from
To understand how other-regarding preferences can be addressed to strengthen PEB, reviewing the experimental findings helps us to identify the underlying mechanisms (i.e.
Effects of electrokinetic phenomena on bacterial deposition monitored by quartz crystal microbalance with dissipation
The world needs effective thermal insulation of buildings for pollution control and energy savings. Optimum thermal, fire and acoustic insulations are achieved by using
In particular, we focus on the thermodynamic aspects of the adsorption process, including dimensional inconsistency of fitted parameters, Temkin isotherm assumptions,
Correlations of dissolved organic carbon (DOC), total nitrogen (TN), ammonia (NH4), and total phosphorus (TN) concentration with selected variables (C3/Tryp and specific
Prediction of soil organic carbon and the C:N ratio on a national scale using machine learning and satellite data: A comparison between Sentinel-2, Sentinel-3 and Landsat-8