Iterative L¨osungsverfahren f¨ur große lineare Gleichungssysteme

f¨ ur

große lineare Gleichungssysteme

Steffen B¨ orm

Stand 25. September 2020

Alle Rechte beim Autor.

1 Einleitung 5

1.1 Direkte L¨ oser f¨ ur schwachbesetzte Matrizen . . . . 6

1.2 Iterationsverfahren . . . . 10

1.3 Semiiterative Verfahren . . . . 12

1.4 Eindimensionales Modellproblem . . . . 14

1.5 Zweidimensionales Modellproblem . . . . 20

2 Lineare Iterationsverfahren 27

2.1 Allgemeine lineare Iterationsverfahren . . . . 27

2.2 Hinreichendes Konvergenzkriterium . . . . 29

2.3 Konvergenz und Spektralradius . . . . 34

2.4 Richardson-Iteration . . . . 41

2.5 Jacobi-Iteration . . . . 45

2.6 Diagonaldominante Matrizen . . . . 55

2.7 Gauß-Seidel-Iteration . . . . 59

2.8 SOR-Iteration . . . . 64

2.9 Kaczmarz-Iteration . . . . 71

3 Semiiterative und Krylow-Raum-Verfahren 75

3.1 Allgemeine lineare semiiterative Verfahren . . . . 75

3.2 Tschebyscheff-Semiiteration . . . . 78

3.3 Gradientenverfahren . . . . 88

3.4 Verfahren der konjugierten Gradienten . . . . 96

3.5 Krylow-Verfahren f¨ ur nicht positiv definite Matrizen . . . . 109

3.6 Verfahren f¨ ur Sattelpunktprobleme . . . . 130

4 Mehrgitterverfahren 135

4.1 Motivation: Zweigitterverfahren . . . . 135

4.2 Mehrgitterverfahren . . . . 147

4.3 Konvergenzbeweis per Fourier-Analyse . . . . 152

4.4 Konvergenz des W-Zyklus-Mehrgitterverfahrens . . . . 156

4.5 Gl¨ attungs- und Approximationseigenschaft bei Finite-Elemente-Verfahren 163 4.6 Symmetrische Mehrgitterverfahren . . . . 172

4.7 Allgemeine Unterraumverfahren . . . . 179

Index 191

Im Mittelpunkt dieser Vorlesung stehen Verfahren zur effizienten Behandlung großer linearer Gleichungssysteme der Form

Ax = b f¨ ur A = (a

)

∈

, x = (x

)

, b = (b

)

∈

(1.1) mit einer n-elementigen allgemeinen Indexmenge I.

Wir haben bereits Algorithmen kennengelernt, mit denen sich derartige Probleme l¨ osen lassen, etwa die Gauß-Elimination (bzw. LR-Faktorisierung), die Cholesky-Faktorisie- rung (f¨ ur symmetrische positiv definite Matrizen) oder die Householder-Zerlegung (bzw.

QR-Faktorisierung). Im allgemeinen Fall w¨ achst der Rechenaufwand dieser Verfahren kubisch in n, also f¨ uhrt eine Verdopplung der Problemdimension zu einer Verachtfa- chung des Rechenaufwands. Der Speicherbedarf w¨ achst quadratisch, eine Verdopplung der Dimension bedeutet also eine Vervierfachung des Speicherbedarfs.

Deshalb lassen sich diese Verfahren nur dann auf große Probleme anwenden, wenn sehr schnelle Rechner (heutzutage in der Regel Parallelrechner, da sich die Leistung einzelner Prozessoren nicht beliebig steigern l¨ asst) mit sehr hoher Speicherkapazit¨ at zur Verf¨ ugung stehen.

Wenn wir ein großes lineares Gleichungssystem l¨ osen wollen, ohne den Gegenwert mehrerer Einfamilienh¨ auser in modernste Rechnertechnik zu investieren, m¨ ussen wir uns also nach alternativen Verfahren umsehen. Dieses Kapitel stellt eine Reihe erfolgreicher Verfahren kurz dar, die detaillierte Behandlung der Algorithmen und die Analyse ihrer Vor- und Nachteile ist sp¨ ateren Kapiteln vorbehalten.

Dieses Skript orientiert sich eng an dem Buch

” Iterative L¨ osung großer schwachbesetz- ter Gleichungssysteme“ von Wolfgang Hackbusch, erschienen 1993 im Teubner-Verlag.

Dieses Buch bietet wesentlich mehr als den hier gegebenen ¨ Uberblick und ist jedem an ite- rativen Verfahren Interessierten w¨ armstens zu empfehlen. Eine erweiterte Version dieses Buchs ist unter der Web-Adresse

zu finden.

Danksagung.

Ich bedanke mich bei Knut Reimer, Christoph Gerken, Jonas Grams,

Jelle Kuiper und Franziska Schwarzenbach f¨ ur Verbesserungsvorschl¨ age und Korrektu-

ren.

1.1 Direkte L¨ oser f¨ ur schwachbesetzte Matrizen

Falls die meisten Eintr¨ age von A gleich Null sind, lassen sich die klassischen L¨ osungsver- fahren so modifizieren, dass sie effizienter arbeiten. In diesem Abschnitt sei I = [1 : n]

Definition 1.1 (Dreiecksmatrizen) Eine Matrix L ∈

nennen wir eine linke untere Dreiecksmatrix, falls

`

= 0 f¨ ur alle i, j ∈ [1 : n] mit i < j gilt, falls also alle Eintr¨ age oberhalb der Diagonalen gleich null sind.

Eine Matrix R ∈

nennen wir eine rechte obere Dreiecksmatrix, falls r

= 0 f¨ ur alle i, j ∈ [1 : n] mit i > j gilt, falls also alle Eintr¨ age unterhalb der Diagonalen gleich null sind.

Wir nennen (L, R) eine LR-Zerlegung einer Matrix A ∈

, falls L ∈

eine linke untere und R ∈

eine rechte obere Dreiecksmatrix ist und A = LR gilt.

Satz 1.2 (Skyline-Struktur) Sei A ∈

invertierbar, und sei (L, R) eine LR- Zerlegung der Matrix A. Dann gelten

(∀k ∈ [1 : j] : a

= 0) ⇒ `

= 0 f¨ ur alle i, j ∈ [1 : n] mit i > j, (∀k ∈ [1 : i] : a

= 0) ⇒ r

= 0 f¨ ur alle i, j ∈ [1 : n] mit i < j.

Falls also am Anfang einer Zeile der Matrix A Nulleintr¨ age auftreten, bleiben sie auch in der Matrix L erhalten. Falls am Anfang einer Spalte der Matrix A Nulleintr¨ age auftreten, bleiben sie auch in der Matrix R erhalten.

Beweis. Wir f¨ uhren den Beweis per Induktion ¨ uber n ∈

. Induktionsanfang: F¨ ur n = 1 ist nichts zu zeigen.

Induktionsvoraussetzung: Sei n ∈

so gegeben, dass die Behauptung f¨ ur alle Matrizen A ∈

gilt.

Induktionsschritt: Sei A ∈

eine Matrix, und sei (L, R) eine LR-Zerlegung dieser Matrix.

Wir zerlegen die Matrizen in A =

A

A

A

a

, A

∈

, A

∈

, A

∈

, L =

L

L

`

, L

∈

, L

∈

, R =

R

R

r

, R

∈

, R

∈

, und stellen fest, dass

A

A

A

a

= A = LR =

L

L

`

R

R

r

=

L

R

L

R

L

R

L

R

+ `

r

gilt, also insbesondere

A

= L

R

, A

= L

R

, A

= L

R

.

Da A invertierbar ist, m¨ ussen auch L und R invertierbar sein. Da die beiden letztge- nannten Dreiecksmatrizen sind, folgt, dass auch L

und R

invertierbar sind.

Seien nun i, j ∈ [1 : n + 1] mit i > j so gegeben, dass a

= 0 f¨ ur alle k ∈ [1 : j] gilt.

Falls i ≤ n gilt, folgt `

= 0 mit der Induktionsvoraussetzung, da (L

, R

) eine LR- Zerlegung der Matrix A

ist. Wir brauchen also nur den Fall i = n + 1 zu betrachten.

Aus unserer Voraussetzung folgt, dass A

dann die Form A

= 0 A

mit A

∈

aufweist. Mit der Zerlegung

R

=

R

R

R

, R

∈

, R

∈

, R

∈

, L

= L

L

, L

∈

, L

∈

folgt aus

0 A

= A

= L

R

= L

L

R

R

R

unmittelbar 0 = L

R

. Da R

als Diagonalblock einer invertierbaren Dreiecksma- trix selbst invertierbar ist, folgen L

= 0 und damit insbesondere `

= 0.

F¨ ur den Nachweis zweite Aussage seien i, j ∈ [1 : n + 1] mit i < j so gegeben, dass a

= 0 f¨ ur alle k ∈ [1 : i] gilt. Falls j ≤ n gilt, folgt `

= 0 wie zuvor mit der Induktionsvoraussetzung. Wir betrachten den Fall j = n + 1. Es gilt

A

=

0

A

mit A

∈

, und mit der Zerlegung

L

= L

L

L

, L

∈

, L

∈

, L

∈

, R

=

R

R

R

∈

, R

∈

folgt aus

0 A

= A

= L

R

= L

L

L

R

R

unmittelbar 0 = L

R

. Da L

als Diagonalblock einer invertierbaren Dreiecksma-

trix selbst invertierbar ist, haben wir R

= 0, also insbesondere r

= 0.

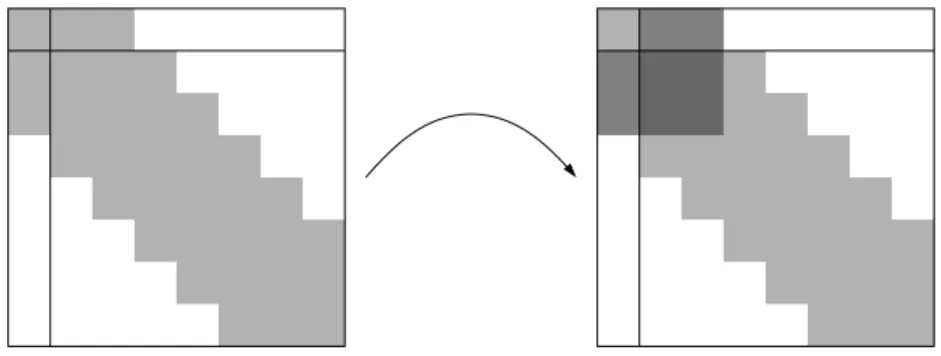
Abbildung 1.1: Konstruktion der Matrix S f¨ ur Bandmatrizen Definition 1.3 (Bandbreite) Sei p ∈

. Falls

|i − j| > p ⇒ a

= 0 f¨ ur alle i, j ∈ I

gilt, nennen wir p eine Bandbreitenschranke f¨ ur A. Die kleinste Bandbreitenschranke nennen wir die Bandbreite von A.

Falls die Matrix A eine durch p beschr¨ ankte Bandbreite besitzt, gilt dasselbe auch f¨ ur die Faktoren L, R ∈

der LR-Zerlegung:

Satz 1.4 (Bandbreitenschranke f¨ ur die LR-Zerlegung) Sei A ∈

invertier- bar, und sei (L, R) eine LR-Zerlegung dieser Matrix.

Sei p ∈

eine Bandbreitenschranke f¨ ur A. Dann ist p auch eine Bandbreitenschranke f¨ ur die Matrizen L und R.

Beweis. Seien i, j ∈ [1 : n] mit |i − j| > p gegeben.

Falls i < j gilt, folgt `

= 0 per Definition. Anderenfalls haben wir i − j > p, also f¨ ur alle k ∈ [1 : j] auch i − k ≥ i − j > p und damit a

= 0. Mit Satz 1.2 folgt `

= 0.

Falls i > j gilt, folgt r

= 0 per Definition. Anderenfalls haben wir j − i > p, also f¨ ur alle k ∈ [1 : i] auch j − k ≥ j − i > p und damit a

= 0. Mit Satz 1.2 folgt r

= 0.

F¨ ur die praktische Konstruktion der LR-Zerlegung empfiehlt sich eine ¨ ahnliche Vor- gehensweise wie im Beweis des Satzes 1.2: Statt die letzte Zeile und Spalte separat zu behandeln, nehmen wir die erste, wir betrachten also

A =

a

A

A

A

, A

∈

, A

∈

, A

∈

und erhalten bei entsprechender Zerlegung der Faktoren L und R die Gleichung

a

A

A

A

= A = LR = `

L

L

r

R

R

=

`

r

`

R

L

r

L

R

+ L

R

, aus der sich die Gleichungen

a

= `

r

, A

= `

R

, A

= L

r

, A

− L

R

= L

R

procedure LRZerlegung(n, p, var A, L, R);

for m := 1 to n do l

← 1;

r

← a

;

for i ∈ [m + 1 : min{m + p, n}] do l

← a

/r

;

r

← a

end for;

for i, j ∈ [m + 1 : min{m + p, n}] do a

← a

− l

r

end for end for

Abbildung 1.2: Berechnung der LR-Zerlegung

ergeben. Mit den ersten drei Gleichungen k¨ onnen wir `

, r

, R

und L

bestimmen.

Die vierte erlaubt es uns dann, L

und R

mit einer LR-Zerlegung der Dimension n −1 zu berechnen. Indem wir die Bandstruktur ausnutzen, sind f¨ ur die Berechnung der linken Seite S := A

− L

R

der vierten Gleichung h¨ ochstens p

Operationen erforderlich, wenn wir A

mit S uberschreiben. Der resultierende Algorithmus ist in Abbildung 1.2 ¨ gegeben. Da wir nur an dem Fall n p interessiert sind, k¨ onnen wir uns die Analyse seiner algorithmischen Komplexit¨ at leicht machen:

Satz 1.5 (Komplexit¨ at der LR-Zerlegung) Der in Abbildung 1.2 gegebene Algo- rithmus ben¨ otigt nicht mehr als np Divisionen, np

Multiplikationen und np

Subtrak- tionen.

Beweis. F¨ ur ein m f¨ uhrt die erste innere Schleife des Algorithmus h¨ ochstens p Divisionen durch, da i nur Werte zwischen m + 1 und m + p annehmen kann.

In der zweiten inneren Schleife k¨ onnen i und j jeweils nur Werte zwischen m + 1 und m +p annehmen, also wird diese Schleife h¨ ochstens p

-mal durchlaufen, so dass h¨ ochstens p

Multiplikationen und Subtraktionen durchzuf¨ uhren sind.

Da die ¨ außere Schleife genau n-mal durchlaufen wird, erhalten wir direkt das gew¨ unschte Ergebnis.

Wir k¨ onnen sehen, dass diese Komplexit¨ atsabsch¨ atzung wesentlich g¨ unstiger als im allgemeinen Fall ist: Falls die Bandbreite von A unabh¨ angig von n beschr¨ ankt ist, k¨ onnen wir die LR-Zerlegung mit einem Aufwand berechnen, der lediglich linear in n w¨ achst.

Sobald die LR-Zerlegung zur Verf¨ ugung steht, k¨ onnen wir das Gleichungssystem b = Ax = LRx durch R¨ uckw¨ artseinsetzen in R und Vorw¨ artseinsetzen in L l¨ osen. Da die Bandbreiten von L und R durch p beschr¨ ankt sind, k¨ onnen diese Berechnungen in O(np) Operationen durchgef¨ uhrt werden, wir erhalten also wieder eine lineare Komplexit¨ at in der Problemdimension n.

Indem wir die besonderen Eigenschaften der Matrix A ausnutzen, k¨ onnen wir so eine

wesentlich h¨ ohere Effizienz erreichen.

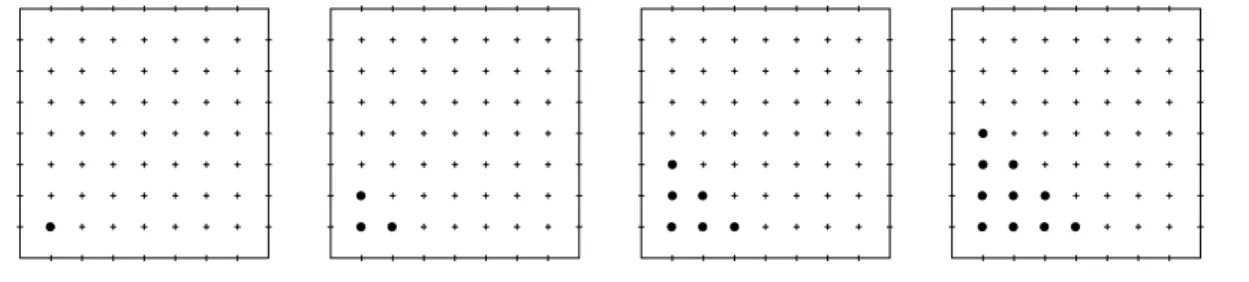
Abbildung 1.3: Auff¨ ullen der Matrix A

Leider ist die Bandbreite vieler in der Praxis auftretender Matrizen nicht beschr¨ ankt.

Es tritt zwar h¨ aufig der Fall auf, dass nur wenige Eintr¨ age der Matrix von Null ver- schieden sind, aber diese Eigenschaft alleine gen¨ ugt nicht, um ¨ ahnliche Aussagen wie in Satz 1.5 zu zeigen.

Ein Beispiel ist in Abbildung 1.3 zu sehen: Obwohl in der Ausgangsmatrix nur jeweils h¨ ochstens vier Eintr¨ age pro Zeile von Null verschieden sind, f¨ ullen die einzelnen Berech- nungsschritte die Matrix A immer weiter auf, bis schließlich die volle Bandbreite von 4 erreicht ist, wir erhalten die von Satz 1.2 vorhergesagte Struktur. In der Praxis treten h¨ aufig Matrizen mit einer Bandbreite von n

auf, hier w¨ urde unser Algorithmus also O(n

) Operationen und O(n

) Speicherpl¨ atze ben¨ otigen, selbst wenn die Ausgangs- matrizen fast nur aus Nulleintr¨ agen bestehen.

1.2 Iterationsverfahren

Wir haben gesehen, dass bei Matrizen, die zwar nur wenige von Null verschiedene Ein- tr¨ age, aber trotzdem eine hohe Bandbreite aufweisen, Algorithmen wie die LR-Zerlegung ineffizient werden, weil sich die Matrix nach und nach auff¨ ullt, also Nulleintr¨ age durch die einzelnen Berechnungsschritte ¨ uberschrieben werden.

Es w¨ are also sehr w¨ unschenswert, ein Verfahren zu kennen, das die Matrix ¨ uberhaupt nicht ver¨ andert und insbesondere auch keine Nulleintr¨ age ¨ uberschreibt.

Dieses Ziel erreichen die meisten iterativen L¨ osungsverfahren. Diese Algorithmen be- rechnen eine Folge x

, x

, . . . von Vektoren, ausgehend von einem beliebigen Startvek- tor x

∈

, die gegen die gew¨ unschte L¨ osung x konvergieren. Im Gegensatz zu LR-, QR- oder Cholesky-Zerlegungen erhalten wir von diesen Verfahren also keine

” exakte“

L¨ osung, sondern lediglich eine approximative L¨ osung, die allerdings beliebig genau ist.

Dieser scheinbare Nachteil wird durch zwei Beobachtungen relativiert: Erstens ist man

bei den meisten Anwendungen ohnehin nicht an einer exakten L¨ osung interessiert, weil

die Ausgangsdaten in der Regel schon gest¨ ort sind, etwa durch Rundungsfehler. Zwei-

tens ist es leichter, bei iterativen Verfahren die Fehlerfortpflanzung zu kontrollieren, weil

in jedem Schritt lediglich die Ausgangsdaten und die aktuelle Approximation eingehen,

aber nicht die vorangehenden Approximationen. Aus diesem Grund werden in der Pra-

xis gelegentlich iterative Verfahren eingesetzt, um die Rundungsfehler zu kompensieren,

die bei einer LR- oder QR-Zerlegung auftreten k¨ onnen (dann spricht man von einer

” Nachiteration“).

Ein sehr einfaches Iterationsverfahren ist die Richardson-Iteration, bei der die Folge der Vektoren durch die Vorschrift

x

:= x

− θ(Ax

− b) f¨ ur alle m ∈

gegeben ist. Hierbei ist θ ∈

ein geeignet zu w¨ ahlender Parameter, der offensichtlich entscheidenden Einfluss auf das Verhalten des Verfahrens hat, beispielsweise bewirkt das Verfahren in komplizierter Weise nichts, wenn wir θ = 0 setzen.

Bereits bei diesem sehr einfachen Beispiel k¨ onnen wir die Vorteile eines iterativen Ver- fahrens erkennen: Neben der Matrix A, dem Vektor b und dem L¨ osungsvektor x (in dem wir die einzelnen Iterierten x

unterbringen) ist lediglich ein Hilfsvektor erforderlich, in dem wir den sogenannten

” Defekt“ d

:= Ax

−b speichern, wir kommen also mit relativ wenig Speicher aus. Die Matrix A tritt ausschließlich in Form der Matrix-Vektor- Multiplikation Ax

auf, insbesondere m¨ ussen wir ihre Eintr¨ age nicht ver¨ andern und vor allem keine Nulleintr¨ age ¨ uberschreiben.

Die Durchf¨ uhrung eines Iterationsschritts, also die Berechnung von x

aus x

, kann in den meisten Anwendungsf¨ allen sehr effizient gestaltet werden, sehr h¨ aufig sogar mit der optimalen Komplexit¨ at O(n).

Leider ist es mit der bloßen Durchf¨ uhrung des Verfahrens nicht getan, wir m¨ ussen auch wissen, wieviele Schritte erforderlich sind, um eine gewisse Genauigkeit zu erzielen, und ob das Verfahren f¨ ur ein bestimmtes Problem ¨ uberhaupt konvergiert. Die Untersuchung der Konvergenz iterativer Verfahren kann sich beliebig kompliziert gestalten, und der Entwurf eines geeigneten Verfahrens f¨ ur eine bestimmte Problemklasse kann auch auf dem heutigen Stand der Forschung noch eine große wissenschaftliche Herausforderung darstellen.

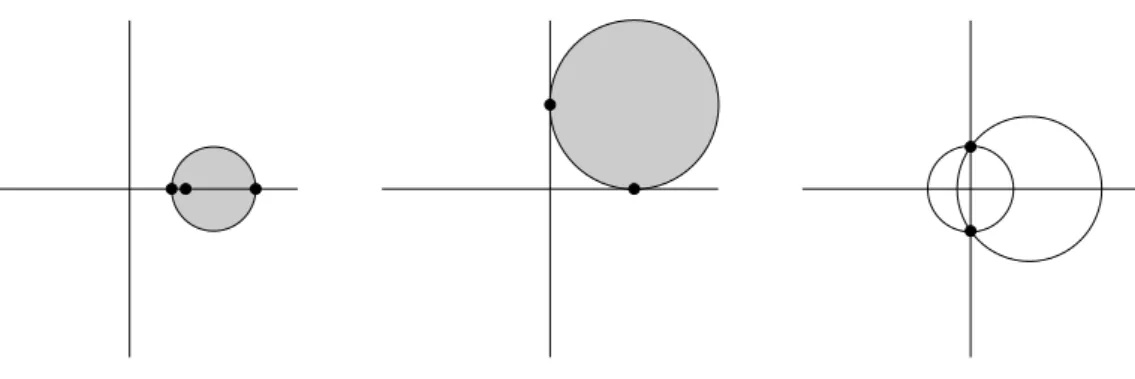
Im Falle des Richardson-Verfahrens l¨ asst sich die Frage nach der Konvergenz relativ einfach beantworten: Das Verfahren konvergiert (f¨ ur ein geeignetes θ), falls alle Eigen- werte der Matrix A in derselben H¨ alfte der komplexen Ebene liegen, falls es also ein z ∈

gibt, das Re(zλ) > 0 f¨ ur alle Eigenwerte λ von A erf¨ ullt.

Wir werden diese Aussage sp¨ ater beweisen, im Augenblick gen¨ ugt es, zwei Beispiele zu untersuchen. Das erste Beispiel ist das durch

A :=

1 0 0 2

, b :=

0 0

gegebene Gleichungssystem Ax = b. Offensichtlich besitzt es die eindeutige L¨ osung x = 0. Falls wir das Richardson-Verfahren auf einen beliebigen Startvektor x

∈

anwenden, erhalten wir

x

= (1 − θ)x

(1 − 2θ)x

!

, x

= (1 − θ)

x

(1 − 2θ)

x

!

, x

= (1 − θ)

x

(1 − 2θ)

x

!

, es folgt somit

kx

k

≤ max{|1 − θ|

, |1 − 2θ|

}kx

k

f¨ ur alle m ∈

,

wir erhalten also Konvergenz f¨ ur alle θ ∈ (0, 1), und die optimale Wahl θ = 2/3 f¨ uhrt zu kx

k

≤

1 3

m

kx

k

f¨ ur alle m ∈

,

also reduziert jeder Schritt des Verfahrens den Fehler um den Faktor % := 1/3. Diese Konvergenzrate h¨ angt nicht von der Gr¨ oße des Gleichungssystems ab, sondern lediglich von dessen Eigenwerten.

Das zweite Beispiel ist das durch A :=

1 0 0 −1

, b :=

0 0

(1.2) gegebene Gleichungssystem Ax = b. Offensichtlich besitzt es ebenfalls die eindeutige L¨ osung x = 0. Falls wir das Richardson-Verfahren auf einen Startvektor x

anwenden, erhalten wir diesmal

x

= (1 − θ)x

(1 + θ)x

!

, x

= (1 − θ)

x

(1 + θ)

x

!

, x

= (1 − θ)

x

(1 + θ)

x

!

. Falls x

6= 0 6= x

gilt, erhalten wir, dass die Folge der Vektoren niemals gegen die korrekte L¨ osung konvergieren wird, weil

max{|1 − θ|, |1 + θ|} =

1 + |θ|

+ 2| Re θ| ≥ 1 gilt. Im schlimmsten Fall, f¨ ur θ 6= 0, wird die Folge sogar divergieren.

Wir k¨ onnen also feststellen, dass die Konvergenz eines iterativen Verfahrens entschei- dend von den Eigenschaften der Matrix A abh¨ angt. Wenn das Verfahren zur Matrix passt, k¨ onnen iterative Verfahren sehr effizient sein, beispielsweise gibt es f¨ ur einige wichtige Klassen von Gleichungssystemen iterative Verfahren, die auch mehrere Millio- nen Unbekannte in wenigen Sekunden berechnen.

1.3 Semiiterative Verfahren

Eine Kombination aus direkten und iterativen Verfahren stellen die sogenannten se- miiterativen Verfahren dar. Diese Algorithmen bestimmen die L¨ osung in einer festen Anzahl von Schritten (¨ ublicherweise n), berechnen dabei aber Zwischenergebnisse, die auch schon gute Approximationen darstellen.

Ein großer Vorteil der Richardson-Iteration besteht darin, dass sie durchgef¨ uhrt wer- den kann, sobald wir eine M¨ oglichkeit besitzen, Matrix-Vektor-Produkte y := Ax zu berechnen. Wir wollen nun ein Verfahren skizzieren, das ebenfalls ausschließlich mit derartigen Produkten auskommt.

Nach dem Satz von Cayley-Hamilton gibt es mindestens ein Polynom π mit einem Grad von h¨ ochstens n derart, dass

π(A) = 0

gilt. Wir w¨ ahlen ein Polynom minimalen Grades p, das diese Gleichung erf¨ ullt, und bezeichnen seine Koeffizienten mit π

, . . . , π

∈

π

A

+ π

A

+ . . . + π

A + π

I = 0

annimmt. Da π minimalen Grad besitzt, muss π

6= 0 gelten (sonst k¨ onnten wir ein Polynom niedrigeren Grades konstruieren, indem wir die obige Gleichung mit A

mul- tiplizieren), und wir erhalten

− π

π

A

+

− π

π

A

+ . . . +

− π

π

A = I.

Nun k¨ onnen wir A entweder nach links oder rechts aus der Summe herausziehen und gelangen zu der Gleichung

− π

π

A

+

− π

π

A

+ . . . +

− π

π

I

A = I, sowie ihrem Gegenst¨ uck

A

− π

π

A

+

− π

π

A

+ . . . +

− π

π

I

= I.

Beide zusammen implizieren

− π

π

A

+

− π

π

A

+ . . . +

− π

π

I = A

. Wir haben also die Inverse von A durch ein Polynom dargestellt.

F¨ ur unsere Aufgabe, also das L¨ osen des Gleichungssystems Ax = b, bedeutet diese Gleichung, dass wir x = A

b in der Form

x =

− π

π

A

b +

− π

π

A

b + . . . +

− π

π

b darstellen k¨ onnen, wir brauchen also lediglich die Vektoren

y

:= b, y

:= Ay

= Ab, y

:= Ay

= A

b, y

:= Ay

= A

b zu berechnen und wissen, dass

x = α

y

+ α

y

+ . . . + α

y

mit den Koeffizienten α

:= −π

/π

gilt.

In der Praxis steht uns das Polynom π nicht zur Verf¨ ugung, wir m¨ ussen also das richtige p und die richtigen Koeffizienten α

anders konstruieren. Krylow-Verfahren gehen dabei so vor, dass der Reihe nach die Vektoren y

berechnet und dann die L¨ osung im zugeh¨ origen Krylow-Raum

K(b, m) := span{y

, . . . , y

} = span{b, . . . , A

b}

gesucht wird. Die Suche nach der L¨ osung l¨ asst sich als lineares Ausgleichsproblem for- mulieren: Wir suchen Koeffizienten α

, . . . , α

∈

derart, dass der Fehler

:= kx − α

y

− . . . − α

y

k

in einer geeigneten Norm (schließlich steht uns x nicht zur Verf¨ ugung) minimiert wird.

Dieses lineare Ausgleichsproblem kann effizient gel¨ ost werden, sofern m nicht zu groß ist.

Wir k¨ onnen diesen Prozess so lange wiederholen, wie die Vektoren y

linear un- abh¨ angig sind. Wenn sie f¨ ur ein m nicht mehr linear unabh¨ angig sein sollten, kann man zeigen, dass

= 0 gelten muss, dass wir also unsere L¨ osung bereits gefunden haben.

Da die Krylow-R¨ aume geschachtelt sind (es gilt offensichtlich K(b, m) ⊆ K(b, m + 1)), muss auch

≥

gelten, und aus dem Satz von Cayley-Hamilton folgt

= 0.

Das Krylow-Verfahren berechnet also eine Folge von Vektoren, die monoton gegen die L¨ osung x konvergiert und nach sp¨ atestens n − 1 Schritten die exakte L¨ osung erreicht.

1.4 Eindimensionales Modellproblem

Wie wir gesehen haben, spielen f¨ ur die verschiedenen skizzierten Verfahren verschiede- ne Eigenschaften des Gleichungssystems eine Rolle: Bei Band-LR-Zerlegungen ist die Bandbreite der Matrix von entscheidender Bedeutung, bei der Richardson-Iteration sind es die Eigenwerte, und auch die Analyse von Krylow-Verfahren l¨ asst sich, zumindest in wichtigen Spezialf¨ allen, auf die Analyse der Eigenwerte zur¨ uckf¨ uhren.

Deshalb ist es sinnvoll, zum Vergleich verschiedener Verfahren einfache Modellproble- me heranzuziehen, bei denen sich die n¨ otigen Eigenschaften leicht nachweisen lassen. Wir beschr¨ anken uns hier auf lineare Gleichungssysteme, die aus der Diskretisierung einer partiellen Differentialgleichung entstehen, denn dieser Ansatz hat den Vorteil, dass wir Matrizen beliebiger Gr¨ oße mit geringem Aufwand aufstellen k¨ onnen und dass sie viele Eigenschaften aufweisen, die auch praktisch auftretende Probleme besitzen.

Zun¨ achst betrachten wir die eindimensionale partielle Differentialgleichung

−u

(x) = f (x) f¨ ur alle x ∈ Ω := (0, 1), (1.3a)

u(0) = u(1) = 0, (1.3b)

f¨ ur eine Funktion u ∈ C[0, 1] mit u|

∈ C

(0, 1) und eine Funktion f ∈ C(0, 1).

Da das Intervall [0, 1] unendlich viele Punkte enth¨ alt, k¨ onnen wir die L¨ osung u in einem Computer mit endlichem Speicher nicht exakt darstellen, m¨ ussen sie also approximieren.

Zu diesem Zweck w¨ ahlen wir ein N ∈

und unterteilen das Intervall [0, 1] in N + 1 Teilintervalle der L¨ ange h := 1/(N + 1). Die Anfangs- und Endpunkte der Intervalle sind durch

ξ

:= hi f¨ ur alle i ∈ {0, . . . , N + 1}

gegeben, und es gilt 0 = ξ

< ξ

< . . . < ξ

< ξ

= 1. Unser Ziel ist es nun, die Werte der Funktion in diesen Punkten zu bestimmen, also

u

:= u(ξ

) f¨ ur alle i ∈ {0, . . . , N + 1}

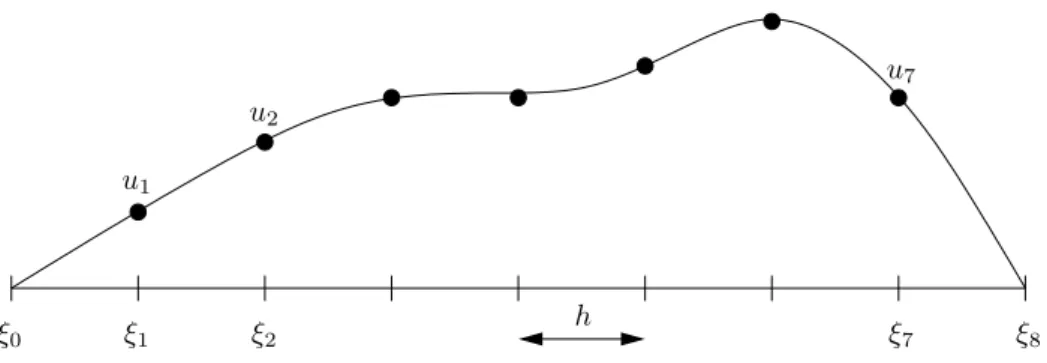
ξ₀ ξ₁ ξ₂ ξ₇ ξ₈ u1

u2

u7

h

Abbildung 1.4: Eindimensionales Modellproblem

zu berechnen. Wegen u

= u(0) = 0 und u

= u(1) = 0 sind nur die Werte u

, . . . , u

∈

zu bestimmen, also der Vektor u = (u

)

f¨ ur I := {1, . . . , N}.

Da uns die wahre L¨ osung u nicht zur Verf¨ ugung steht, m¨ ussen wir versuchen, ihre Ableitung u

zu approximieren, indem wir nur die Werte u

, . . . , u

verwenden. Wir nehmen an, dass u ∈ C

[0, 1] gilt und wenden die Taylor-Entwicklung an, um die Glei- chungen

u(x + h) = u(x) + hu

(x) + h

2 u

(x) + h

6 u

(x) + h

24 u

(η

), u(x − h) = u(x) − hu

(x) + h

2 u

(x) − h

6 u

(x) + h

24 u

(η

)

f¨ ur geeignete η

∈ [x, x + h] und η

∈ [x − h, x] zu erhalten. Wir addieren beide Glei- chungen und finden

u(x + h) + u(x − h) = 2u(x) + h

u

(x) + h

24 u

(η

) + h

24 u

(η

).

Wir sortieren die Terme um und stellen fest, dass

u

(x) − 1

h

(u(x − h) − 2u(x) + u(x + h))

≤ h

12 ku

k

(1.4) gilt, also k¨ onnen wir

1

h

(u(x − h) − 2u(x) + u(x + h)) ≈ u

(x) (1.5) als Endergebnis festhalten. Angewendet auf die Punkte ξ

, . . . , ξ

bedeutet diese Glei- chung

1

h

(u

− 2u

+ u

) ≈ u

(ξ

).

Um die Verbindung zur Differentialgleichung (1.3) herzustellen, f¨ uhren wir den Vektor f = (f

)

mit

f

= f (ξ

) f¨ ur alle i ∈ I

ein und erhalten wegen f

= −u

(ξ

) die diskrete Approximation 1

h

(−u

+ 2u

− u

) = f

f¨ ur alle i ∈ I

der Differentialgleichung (1.3). Wie wir sehen, handelt es sich dabei um ein lineares Gleichungssystem

1 h















2 −1

−1 2 −1 . .. ... ...

−1 2 −1

−1 2





























u

u

.. . u

u















=















f

f

.. . f

f















,

das mit Hilfe der durch

L

=







2h

falls i = j,

−h

falls |i − j| = 1,

0 sonst

f¨ ur alle i, j ∈ I

und L = (L

)

gegebenen Matrix in der kompakten Form Lu = f

dargestellt werden kann. An der Definition von L kann man leicht ablesen, dass diese Matrix eine Bandbreite von 1 besitzt, also l¨ asst sich das Gleichungssystem mit den in Abschnitt 1.1 eingef¨ uhrten Verfahren sehr effizient l¨ osen.

Die Fehlerabsch¨ atzung (1.4) legt uns nahe, dass wir nur dann auf eine gute Genauigkeit hoffen d¨ urfen, wenn h klein ist. Wegen h = 1/(N +1) k¨ onnen wir dieses Ziel nur erreichen, indem wir die Anzahl N der Unbekannten relativ groß w¨ ahlen.

F¨ ur die Untersuchung des Richardson-Verfahrens ben¨ otigen wir die Eigenwerte der Matrix L, die sich mit Hilfe von etwas trigonometrischer Arithmetik bestimmen lassen.

Lemma 1.6 (Trigonometrische Orthogonalbasis) Sei N ∈

und h := 1/(N + 1).

Es gilt

N

X

j=1

sin(πjkh) sin(πj`h) =

(

(N + 1)/2 falls k = `,

0 ansonsten f¨ ur alle k, ` ∈ [1 : N ].

Beweis. Seien k, ` ∈ [1 : N ] gegeben. Mit der Eulerschen Gleichung gilt

N

X

j=1

sin(πjkh) sin(πj`h) =

N

X

j=1

e

− e

2i

e

− e

2i

= 1 4

N

X

j=1

e

+ e

− e

− e

,

und wegen k + ` ∈ [2 : 2N ] gilt (k + `)h ∈ (0, 2), also folgen q := e

6= 1 und

N

X

j=1

e

=

N

X

j=1

q

= q

− q

q − 1 = σ − q q − 1

f¨ ur σ := q

= e

∈ {−1, 1}. In derselben Weise erhalten wir f¨ ur p := e

die Gleichung

N

X

j=1

e

=

N

X

j=1

p

=

(

N falls k = `,

σ−p

p−1

ansonsten,

da aus k + ` = (k − `) + 2` auch σ = e

= p

folgt. F¨ ur k = ` haben wir σ = 1, also

N

X

j=1

sin(πjkh) sin(πj`h) = 1 4

2N − σ − q

q − 1 − σ − q q − 1

= N 2 − 1

2 Re (1 − q)(¯ q − 1)

|q − 1|

= N 2 + 1

2 Re (q − 1)(¯ q − 1)

|q − 1|

= N + 1 2 .

F¨ ur k 6= ` m¨ ussen wir die F¨ alle σ = 1 und σ = −1 unterscheiden. Im ersten Fall gilt

N

X

j=1

sin(πjkh) sin(πj`h) = 1 4

σ − p

p − 1 + σ − p

p − 1 − σ − q

q − 1 − σ − q q − 1

= 1 4 Re

1 − p

p − 1 − 1 − q q − 1

= 1

4 (−1 + 1) = 0, im zweiten Fall erhalten wir

N

X

j=1

sin(πjkh) sin(πj`h) = 1 4

σ − p

p − 1 + σ − p

p − 1 − σ − q

q − 1 − σ − q q − 1

= 1 4 Re

−1 − p

p − 1 − −1 − q q − 1

= 1 4 Re

(−1 − p)(¯ p − 1)

|p − 1|

− (−1 − q)(¯ q − 1)

|q − 1|

= 1 4 Re

1 − |p|

− p ¯ + p

|p − 1|

− 1 − |q|

− q ¯ + q

|q − 1|

= 1 4 Re

p − p ¯

|p − 1|

− q − q ¯

|q − 1|

= 0, und damit ist die gew¨ unschte Orthonormalit¨ atsbeziehung bewiesen.

Lemma 1.7 (Eigenwerte) F¨ ur alle k ∈ I definieren wir den Vektor e

∈

durch e

:= √

2h sin(πjkh) f¨ ur alle j ∈ I . Es gilt

Le

= λ

e

mit λ

:= 4h

sin

(πkh/2) f¨ ur alle k ∈ I,

und die Vektoren erf¨ ullen he

, e

i

=

(

1 falls k = `,

0 ansonsten f¨ ur k, ` ∈ I,

bilden also eine aus Eigenvektoren der Matrix L bestehende Orthonormalbasis von

. Beweis. Sei k ∈ I . Um nachzuweisen, dass e

ein Eigenvektor ist, betrachten wir f¨ ur einen Index j ∈ I die j-te Komponente von Le

: Wegen sin(π0kh) = 0 = sin(π(N + 1)kh) erhalten wir

(Le

)

= h

(2e

− e

− e

)

= √

2hh

(2 sin(πjkh) − sin(π(j − 1)kh) − sin(π(j + 1)kh)).

Wir wenden das Additionstheorem sin(x + y) = sin(x) cos(y) + cos(x) sin(y) an:

(Le

)

=

√

2hh

(2 sin(πjkh) − sin(πjkh) cos(−πkh) − cos(πjkh) sin(−πkh)

− sin(πjkh) cos(πkh) − cos(πjkh) sin(πkh))

=

√

2hh

(2 − 2 cos(πkh)) sin(πjkh).

Nun benutzen wir das Additionstheorem cos(2x) = 2 cos

(x) − 1:

(Le

)

=

√

2hh

(2 − 4 cos

(πkh/2) + 2) sin(πjkh)

= 4 √

2hh

(1 − cos

(πkh/2)) sin(πjkh)

= 4 √

2hh

sin

(πkh/2) sin(πjkh)

= λ

e

= (λ

e

)

.

Da πkh/2 = πk/(2(N + 1)) ∈ (0, π/2) f¨ ur alle k ∈ I = {1, . . . , N} gilt und die Sinus- funktion auf diesem Intervall streng monoton w¨ achst, sind alle Eigenwerte verschieden, also m¨ ussen alle Eigenvektoren e

linear unabh¨ angig sein.

Seien nun k, ` ∈ I. Mit Lemma 1.6 erhalten wir he

, e

i

= 2h

N

X

j=1

sin(πjkh) sin(πj`h) = 2h

(

(N + 1)/2 falls k = `,

0 ansonsten

=

(

1 falls k = `, 0 ansonsten.

Untersuchen wir nun das Verhalten der Richardson-Iteration f¨ ur die Matrix L. Wir betrachten wieder das vereinfachte System Lu = 0, das die exakte L¨ osung u = 0 besitzt.

Den Startvektor u

∈

stellen wir in der Eigenvektorbasis dar und erhalten u

=

k∈I

α

e

,

so dass sich der Iterationsschritt

u

= u

− θLu

in der Form

u

=

k∈I

α

(1 − θλ

)e

(1.6)

darstellen l¨ asst. F¨ ur die weiteren Iterierten erhalten wir die Darstellung u

=

k∈I

α

(1 − θλ

)

e

in der Eigenvektorbasis, also konvergiert die Iteration gegen die korrekte L¨ osung u = 0, falls

max{|1 − θλ

| : k ∈ I} < 1 (1.7) gilt. Gl¨ ucklicherweise gen¨ ugt es, nur den gr¨ oßten und den kleinsten Eigenwert zu unter- suchen, also

λ

= 4h

sin

(πh/2), λ

= 4h

sin

(πN h/2) = 4h

cos

(πh/2).

Wenn wir max{|1 − θλ

|, |1 − θλ

|} < 1 bewiesen haben, gilt auch die Bedingung (1.7).

Wir w¨ ahlen θ so, dass diese Gr¨ oße minimiert wird, n¨ amlich als L¨ osung von 1 − θ

λ

= θ

λ

− 1.

Diese L¨ osung ist durch

θ

:= 2 λ

+ λ

= 2

4h

= h

2 gegeben und f¨ uhrt zu der Schranke

max{|1 − θ

λ

| : k ∈ I} = % := 1 − θ

λ

= 1 − 2λ

λ

+ λ

= λ

− λ

λ

+ λ

< 1.

Mit dieser Schranke und der Dreiecksungleichung erhalten wir ku

k ≤ %

k∈I

kα

e

k f¨ ur jede beliebige Norm. F¨ ur die euklidische Norm gilt sogar

ku

k

≤ %

ku

k

,

da wir bereits nachgewiesen haben, dass die Eigenvektoren senkrecht zueinander stehen.

Die Richardson-Iteration konvergiert also. Leider konvergiert sie nicht sehr schnell: Wir haben

% = λ

− λ

λ

+ λ

= 4h

cos

(πh/2) − 4h

sin

(πh/2)

4h

(1.8)

= cos

(πh/2) − sin

(πh/2) = 1 − 2 sin

(πh/2),

und f¨ ur h → 0, also N → ∞, bedeutet diese Gleichung % ≈ 1 − π

h

/2, die Konvergenz-

rate wird also schlechter, wenn die Problemdimension w¨ achst.

h h

iy

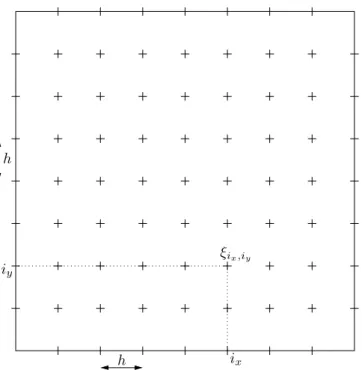
i_x ξi_x,i_y

Abbildung 1.5: Zweidimensionales Modellproblem f¨ ur N = 7

1.5 Zweidimensionales Modellproblem

W¨ ahrend das eindimensionale Modellproblem (und auch viele andere eindimensionale Probleme) zu Matrizen geringer Bandbreite f¨ uhrt und somit effizient mit der Band-LR- Zerlegung gehandhabt werden kann, wird die Situation wesentlich schwieriger, wenn wir zu einem zweidimensionalen Problem ¨ ubergehen: Wir untersuchen die partielle Differen- tialgleichung

−∆u(x) :=

− ∂

∂x

− ∂

∂x

u(x) = f(x) f¨ ur alle x ∈ Ω := (0, 1)

, (1.9a) u(x) = 0 f¨ ur alle x ∈ ∂Ω = {0, 1} × [0, 1] (1.9b)

∪ [0, 1] × {0, 1}, f¨ ur eine Funktion u ∈ C(Ω) mit u|

∈ C

(Ω) und eine rechte Seite f ∈ C(Ω).

Diese Differentialgleichung ist das zweidimensionale Gegenst¨ uck zu der Gleichung (1.3). Wir diskretisieren sie, indem wir eine endliche Anzahl von Punkten in Ω fixieren und die zweite Ableitung mit Hilfe der Funktionswerte in diesen Punkten approximieren.

Die Punkte konstruieren wir ¨ ahnlich wie im eindimensionalen Fall: Wir fixieren N ∈

, setzen h := 1/(N + 1) und w¨ ahlen

ξ

:= (hi

, hi

) f¨ ur alle i

, i

∈ {0, . . . , N + 1}.

Infolge der Randbedingung sind nur die Werte

u

:= u(ξ

) f¨ ur alle i

, i

∈ {1, . . . , N}

zu bestimmen.

Zur Vereinfachung der Notation fassen wir i

und i

zu einem Multiindex i := (i

, i

) zusammen und bezeichnen die Menge aller dieser Multiindizes mit

I := {i = (i

, i

) : i

, i

∈ {1, . . . , N }}.

Die M¨ achtigkeit der neuen Indexmenge I betr¨ agt n := N

, und mit ihrer Hilfe k¨ onnen wir die Notationen des eindimensionalen Problems weiterverwenden: ξ

= (hi

, hi

), u

= u(ξ

) = u(hi

, hi

). Der Vektor der Werte von u schreibt sich als u = (u

)

.

Um die Differentialgleichung (1.9) zu diskretisieren, ersetzen wir wieder die zweiten Ableitungen durch die Approximation (1.5) und erhalten

1 h

u

x

− h x

− 2u x

x

+ u

x

+ h x

≈ ∂

∂x

u x

x

, 1

h

u

x

x

− h

− 2u x

x

+ u

x

x

+ h

≈ ∂

∂x

u x

x

f¨ ur alle x = x

x

∈ Ω.

Wie bereits im eindimensionalen Fall wenden wir diese Gleichungen auf die Punkte ξ

an und erhalten

1

h

4u

− u

− u

− u

− u

≈ −∆u(ξ

) f¨ ur alle i ∈ I . Wir f¨ uhren wieder den Vektor f ∈

mit

f

= f(ξ

) = f (hi

, hi

) f¨ ur alle i ∈ I ein und setzen −∆u(ξ

) = f

, um die diskrete Approximation

1

h

4u

− u

− u

− u

− u

= f

f¨ ur alle i ∈ I der Differentialgleichung (1.9) zu erhalten.

Mit Hilfe der Matrix L = (L

)

, gegeben durch

L

=















4h

falls i

= j

, i

= j

,

−h

falls |i

− j

| = 1, i

= j

,

−h

falls |i

− j

| = 1, i

= j

,

0 sonst

f¨ ur alle i, j ∈ I,

k¨ onnen wir das lineare Gleichungssystem wieder in der kompakten Form

Lu = f

procedure MVMModell2D(N , x, var y);

h ← 1/(N + 1);

α ← 4h

; β ← −h

; for i

∈ {1, . . . , N } do

for i

∈ {1, . . . , N} do y

← αx

; if i

> 1 then

y

← y

+ βx

end if;

if i

< N then

y

← y

+ βx

end if;

if i

> 1 then

y

← y

+ βx

end if;

if i

< N then

y

← y

+ βx

end if

end for end for

Abbildung 1.6: Berechnung von y := Lx

schreiben. Da I keine Teilmenge von

ist, k¨ onnen wir keine direkte Aussage ¨ uber die Bandbreite von L treffen. Wir k¨ onnen allerdings versuchen, die Indexmenge I durch die Menge

:= {1, . . . , n} mit n = |I| = N

zu ersetzen. Formal geschieht dies durch die Wahl einer bijektiven Abbildung

ι : I →

,

die die Multiindizes i = (i

, i

) ∈ I durchnumeriert. F¨ ur so ein ι k¨ onnen wir dann Matrizen L

∈

und Vektoren u

, f

∈

durch

L

:= L

, u

:= u

, f

:= f

f¨ ur alle i, j ∈ I definieren und feststellen, dass das Gleichungssystem Lu = f und das

” numerierte“

Gleichungssystem

L

u

= f

vollst¨ andig gleichwertig sind.

Es stellt sich die Frage, ob es eine von n (also von N ) unabh¨ angige Bandbreiten- schranke k f¨ ur L

geben kann. Im eindimensionalen Fall war sogar k = 1 akzeptabel, im zweidimensionalen Fall ist die Situation komplizierter:

Lemma 1.8 (Minimale Bandbreite) Sei k ∈

eine Bandbreitenschranke f¨ ur L

.

Dann gilt k ≥ (N + 1)/4.

Abbildung 1.7: Mengen G

, G

, G

und G

f¨ ur den Fall N = 7 Beweis. Wir betrachten die Folge

G

:= {(1, 1)},

G

:= {j ∈ I : ∃i ∈ G

: L

6= 0} = {(1, 1), (2, 1), (1, 2)},

G

:= {j ∈ I : ∃i ∈ G

: L

6= 0} = {(1, 1), (2, 1), (1, 2), (3, 1), (2, 2), (1, 3)}, G

:= {j ∈ I : ∃i ∈ G

: L

6= 0}.

Man kann sich einfach ¨ uberlegen, dass

|G

| = |G

| + m + 1 f¨ ur alle m ∈ [1 : N − 1]

gilt (siehe Abbildung 1.7), und die Gauß’sche Summenformel ergibt

|G

| = (m + 2)(m + 1)

2 f¨ ur alle m ∈ [1 : N − 1]. (1.10)

Wir untersuchen nun die M¨ achtigkeit der Mengen ι(G

). Wir zeigen

ι(G

) ⊆ {j ∈

: |j − c| ≤ km} (1.11) per Induktion f¨ ur c := ι(1, 1). F¨ ur m = 0 ist die Aussage (1.11) offensichtlich.

Nehmen wir nun an, dass (1.11) f¨ ur ein m ∈

gilt. Sei j ∈ G

. Nach Definition gibt es ein i ∈ G

mit L

6= 0, also gilt auch L

6= 0. Da k eine Bandbreitenschranke f¨ ur L

ist, folgt |ι(i) − ι(j)| ≤ k. Die Induktionsannahme impliziert |ι(i) − c| ≤ km, also erhalten wir |ι(j) − c| ≤ |ι(j) − ι(i)| + |ι(i) − c| ≤ k(m + 1). Damit ist (1.11) auch f¨ ur m + 1 bewiesen.

Aus (1.11) folgt #ι(G

) ≤ 2km + 1, und da ι eine Bijektion ist, erhalten wir (m + 2)(m + 1)

2 = |G

| = |ι(G

)| ≤ 2km + 1 f¨ ur alle m ∈ [0 : N − 1].

Wir haben k ≥ 1, also folgt (m + 2)(m + 1)

2 ≤ 2km + 1 ≤ 2km + 2k = 2k(m + 1)